2.6.2 菱形的判定 课件(共19张PPT)
文档属性
| 名称 | 2.6.2 菱形的判定 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
菱形的判定
湘教版·八年级下册
上课课件
第2章
四边形
学习目标
【知识与技能】
1.经历利用菱形的定义探究其他判定方法的过程,培养学生的动手实验、观察、推理意识,发展学生的形象思维和逻辑推理能力.
2.根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力.
【过程与方法】
尝试从不同角度寻求菱形的判定方法,并能有效的解决问题,尝试评价不同判定方法之间的差异,通过对菱形判定过程的反思,获得灵活判定四边形是菱形的经验.
【情感态度】
在探究菱形的判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
【教学重点】
菱形判定方法的探究
【教学难点】
菱形判定方法的探究及灵活运用
新课导入
(1)什么叫菱形?
(2)菱形是特殊的平行四边形,除了它之外,还有其他判别方法吗?
一组邻边相等的平行四边形叫作菱形.
用
4
支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:四条边都相等的四边形是菱形吗?
你能试着证明吗?
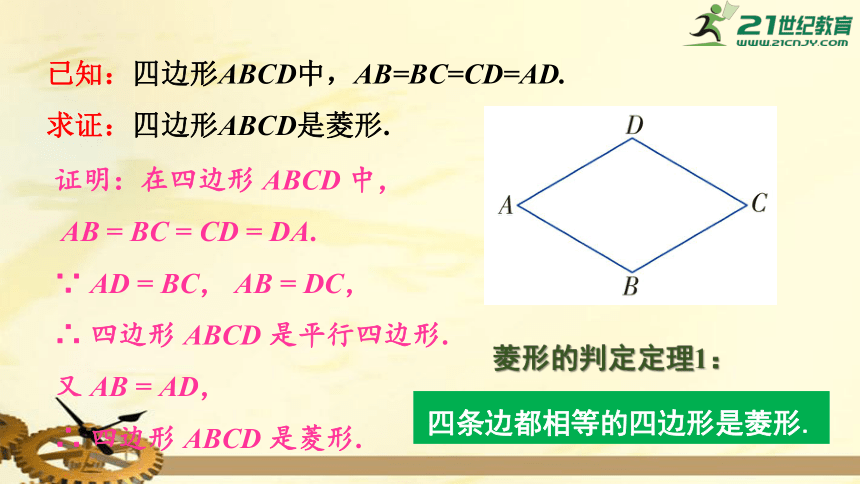
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形
ABCD
中,
AB
=
BC
=
CD
=
DA.
∵
AD
=
BC,
AB
=
DC,
∴
四边形
ABCD
是平行四边形.
又
AB
=
AD,
∴
四边形
ABCD
是菱形.
菱形的判定定理1:
四条边都相等的四边形是菱形.
已知:如图,在四边形
ABCD
中,线段
BD
垂直平分
AC,且相交于点
O,∠1
=∠2.
求证:四边形
ABCD
是菱形.
证明
∵线段
BD
垂直平分AC
,
∴
BA
=
BC,DA
=
DC,OA
=
OC.
在△AOB
和△COD
中,
∵∠1
=∠2,∠AOB
=∠COD,OA
=
OC.
∴△OAB≌△OCD.
∴
AB
=
CD.
∴BA
=
BC
=
CD
=
DA.
∴四边形
ABCD
是菱形(四条边都相等的四边形是菱形).
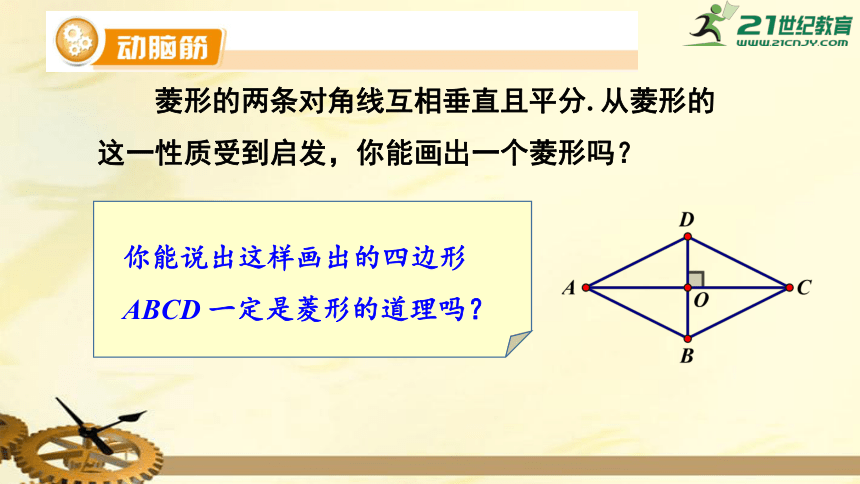
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
你能说出这样画出的四边形ABCD
一定是菱形的道理吗?
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
由画法可知,四边形
ABCD
的两条对角线
AC
与
BD
互相平分,因此它是平行四边形.
又已知其对角线互相垂直,上述问题抽象出来就是:对角线互相垂直的平行四边形是菱形吗?
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
证明:∵
在
□
ABCD中,AC⊥BD,OA=
OC,
∴BD
所在的直线是
AC
的垂直平分线.
∴
DA=
DC.
∴
□
ABCD
是菱形.
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
如图,在□
ABCD
中,AC
=
6,BD
=
8,AD
=
5.
求
AB
的长.
∴
AB
=
AD
=
5
.
解
∵
四边形
ABCD
为平行四边形,
∴
△DAO
是直角三角形.
∴
∠DOA
=
90°,即
DB⊥AC.
∴
□
ABCD是菱形.(对角线互相垂直
的平行四边形是菱形)
又∵
AD
=
5,满足
AD2
=
OA2
+
OD2,
练习
【教材P70】
画一个菱形,使它的两条对角线长度分别为
4
cm,3
cm.
画法:
AC
=
4
cm,
BD
=
3cm,
O
为
AC,BD
的中点,
且
AC
⊥
BD.
证明:在Rt△BON和Rt△DOM
中,
∵
BO
=
DO,
∠DBN
=
∠BDM,
∴
Rt△BON≌Rt△DOM.
∴OM=ON.
∵BD,NM
是四边形
BNDM的两条对角线且互相平分,
∴四边形
BNDM
是平行四边形.
又
MN⊥BD,
∴四边形
BNDM
是菱形.
【教材P70】
2.
如图,在平行四边形
ABCD
中,对角线
AC,BD
相交于点
O,过点
O
作
MN⊥BD,分别交
AD,BC
于点M,N
.
求证:四边形
BNDM
是菱形.
随堂练习
能判定一个四边形是菱形的条件是(
)
A.对角线相等且互相垂直
B.对角线相等且互相平分
C.对角线互相垂直
D.对角线互相垂直平分
D
(河南中考)如图,在□
ABCD
中,
对角线
AC,
BD
相交于点
O,
添加下列条件不能判定
□
ABCD
是菱形的是(
)
A.
AC⊥BD
B.
AB=BC
C.
AC=BD
D.
∠1=∠2
C
是菱形.
理由如下:
∵△ABC
为等腰三角形,∴AB=BC.
∵△CDA为等腰三角形,∴CD=AD.
而△CDA是△ABC的像,∴AB=BC=CD=DA.
∴四边形
ABCD
是菱形.
如图,把等腰三角形
ABC
绕它的底边
AC
上的中点
O
旋转180°,得到三角形
CDA,试问:
四边形
ABCD
是菱形吗?为什么?
菱形的判定定理1:
四条边都相等的四边形是菱形.
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
菱形的判定
湘教版·八年级下册
上课课件
第2章
四边形
学习目标
【知识与技能】
1.经历利用菱形的定义探究其他判定方法的过程,培养学生的动手实验、观察、推理意识,发展学生的形象思维和逻辑推理能力.
2.根据菱形的判定定理进行简单的证明,培养学生的逻辑推理能力和演绎能力.
【过程与方法】
尝试从不同角度寻求菱形的判定方法,并能有效的解决问题,尝试评价不同判定方法之间的差异,通过对菱形判定过程的反思,获得灵活判定四边形是菱形的经验.
【情感态度】
在探究菱形的判定方法的活动中获得成功的体验,通过运用菱形的判定和性质,锻炼克服困难的意志,建立自信心.
【教学重点】
菱形判定方法的探究
【教学难点】
菱形判定方法的探究及灵活运用
新课导入
(1)什么叫菱形?
(2)菱形是特殊的平行四边形,除了它之外,还有其他判别方法吗?
一组邻边相等的平行四边形叫作菱形.
用
4
支长度相等的铅笔能摆成菱形吗?
把上述问题抽象出来就是:四条边都相等的四边形是菱形吗?
你能试着证明吗?
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:在四边形
ABCD
中,
AB
=
BC
=
CD
=
DA.
∵
AD
=
BC,
AB
=
DC,
∴
四边形
ABCD
是平行四边形.
又
AB
=
AD,
∴
四边形
ABCD
是菱形.
菱形的判定定理1:
四条边都相等的四边形是菱形.
已知:如图,在四边形
ABCD
中,线段
BD
垂直平分
AC,且相交于点
O,∠1
=∠2.
求证:四边形
ABCD
是菱形.
证明
∵线段
BD
垂直平分AC
,
∴
BA
=
BC,DA
=
DC,OA
=
OC.
在△AOB
和△COD
中,
∵∠1
=∠2,∠AOB
=∠COD,OA
=
OC.
∴△OAB≌△OCD.
∴
AB
=
CD.
∴BA
=
BC
=
CD
=
DA.
∴四边形
ABCD
是菱形(四条边都相等的四边形是菱形).
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
你能说出这样画出的四边形ABCD
一定是菱形的道理吗?
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
由画法可知,四边形
ABCD
的两条对角线
AC
与
BD
互相平分,因此它是平行四边形.
又已知其对角线互相垂直,上述问题抽象出来就是:对角线互相垂直的平行四边形是菱形吗?
菱形的两条对角线互相垂直且平分.
从菱形的这一性质受到启发,你能画出一个菱形吗?
证明:∵
在
□
ABCD中,AC⊥BD,OA=
OC,
∴BD
所在的直线是
AC
的垂直平分线.
∴
DA=
DC.
∴
□
ABCD
是菱形.
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
如图,在□
ABCD
中,AC
=
6,BD
=
8,AD
=
5.
求
AB
的长.
∴
AB
=
AD
=
5
.
解
∵
四边形
ABCD
为平行四边形,
∴
△DAO
是直角三角形.
∴
∠DOA
=
90°,即
DB⊥AC.
∴
□
ABCD是菱形.(对角线互相垂直
的平行四边形是菱形)
又∵
AD
=
5,满足
AD2
=
OA2
+
OD2,
练习
【教材P70】
画一个菱形,使它的两条对角线长度分别为
4
cm,3
cm.
画法:
AC
=
4
cm,
BD
=
3cm,
O
为
AC,BD
的中点,
且
AC
⊥
BD.
证明:在Rt△BON和Rt△DOM
中,
∵
BO
=
DO,
∠DBN
=
∠BDM,
∴
Rt△BON≌Rt△DOM.
∴OM=ON.
∵BD,NM
是四边形
BNDM的两条对角线且互相平分,
∴四边形
BNDM
是平行四边形.
又
MN⊥BD,
∴四边形
BNDM
是菱形.
【教材P70】
2.
如图,在平行四边形
ABCD
中,对角线
AC,BD
相交于点
O,过点
O
作
MN⊥BD,分别交
AD,BC
于点M,N
.
求证:四边形
BNDM
是菱形.
随堂练习
能判定一个四边形是菱形的条件是(
)
A.对角线相等且互相垂直
B.对角线相等且互相平分
C.对角线互相垂直
D.对角线互相垂直平分
D
(河南中考)如图,在□
ABCD
中,
对角线
AC,
BD
相交于点
O,
添加下列条件不能判定
□
ABCD
是菱形的是(
)
A.
AC⊥BD
B.
AB=BC
C.
AC=BD
D.
∠1=∠2
C
是菱形.
理由如下:
∵△ABC
为等腰三角形,∴AB=BC.
∵△CDA为等腰三角形,∴CD=AD.
而△CDA是△ABC的像,∴AB=BC=CD=DA.
∴四边形
ABCD
是菱形.
如图,把等腰三角形
ABC
绕它的底边
AC
上的中点
O
旋转180°,得到三角形
CDA,试问:
四边形
ABCD
是菱形吗?为什么?
菱形的判定定理1:
四条边都相等的四边形是菱形.
菱形的判定定理2:
对角线互相垂直的平行四边形是菱形.
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
