2.6.1 菱形的性质 课件(共24张PPT)
文档属性
| 名称 | 2.6.1 菱形的性质 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
菱形的性质
湘教版·八年级下册
上课课件
第2章
四边形
学习目标
【知识与技能】
1.理解并掌握菱形的定义及性质定理1、2;会用这些定理进行有关的论证和计算.
2.培养学生的观察能力、动手能力、自学能力、计算能力、逻辑思维能力.
3.通过运用菱形知识解决具体问题,提高分析能力和观察能力.
4.根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.
【过程与方法】
经历探索菱形的性质和基本概念的过程,在操作、观察、分析过程中发展学生思维意识,体会几何说理的基本方法.
【情感态度】
培养学生主动探究的习惯和严密的思维意识、审判观、价值观.并在教学中渗透事物总是相互联系又是相互区别的辩证唯物主义观点.
【教学重点】
菱形的性质定理
【教学难点】
定理的证明方法及运用
新课导入
将一张矩形的纸对折,然后沿着图中的虚线剪下,猜猜看,打开是个什么图形,自己动手做一做.
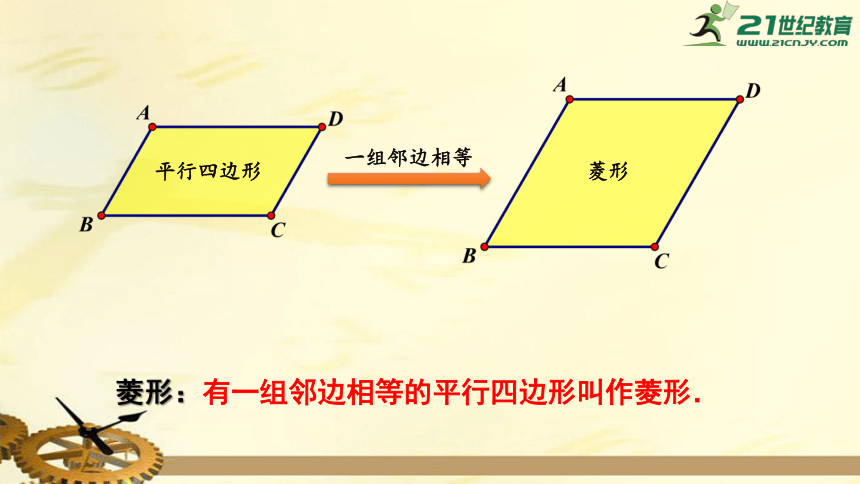
观察图中的平行四边形,它们有什么特点?
它们的邻边相等.
平行四边形
菱形
一组邻边相等
菱形:有一组邻边相等的平行四边形叫作菱形.
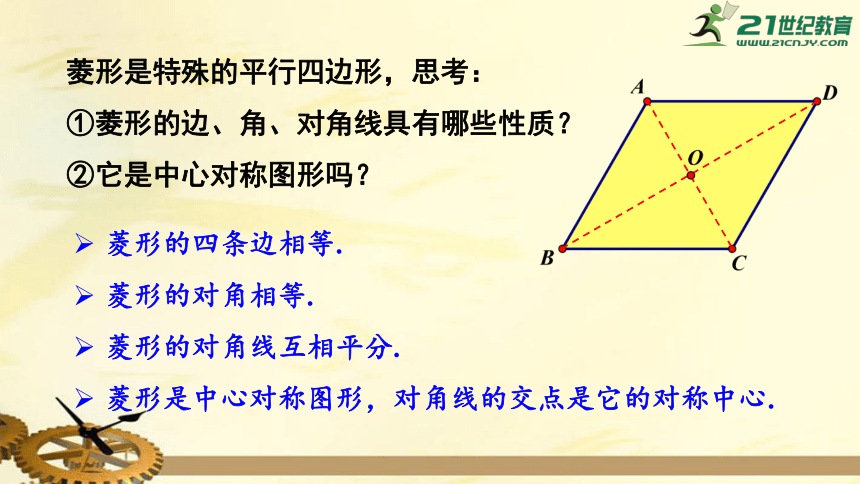
菱形是特殊的平行四边形,思考:
①菱形的边、角、对角线具有哪些性质?
②它是中心对称图形吗?
菱形的四条边相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形是中心对称图形,对角线的交点是它的对称中心.
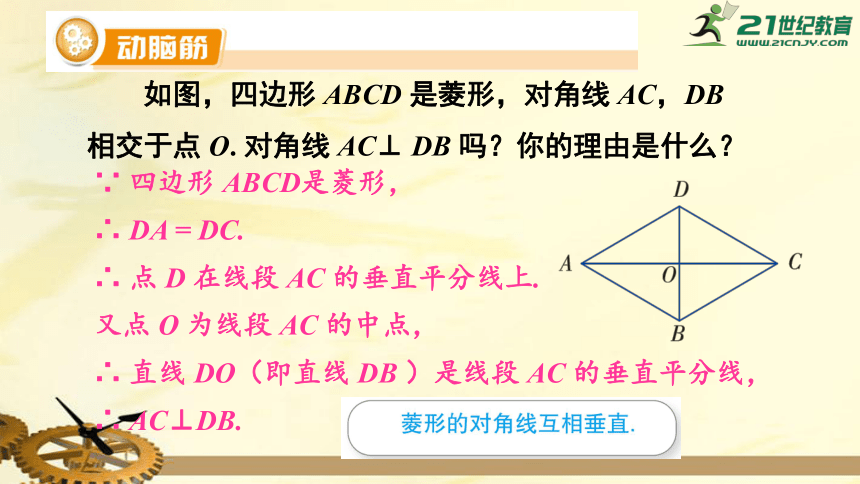
如图,四边形
ABCD
是菱形,对角线
AC,DB
相交于点
O.
对角线
AC⊥
DB
吗?你的理由是什么?
∵
四边形
ABCD是菱形,
∴
DA
=
DC.
∴
点
D
在线段
AC
的垂直平分线上.
又点
O
为线段
AC
的中点,
∴
直线
DO(即直线
DB
)是线段
AC
的垂直平分线,
∴
AC⊥DB.
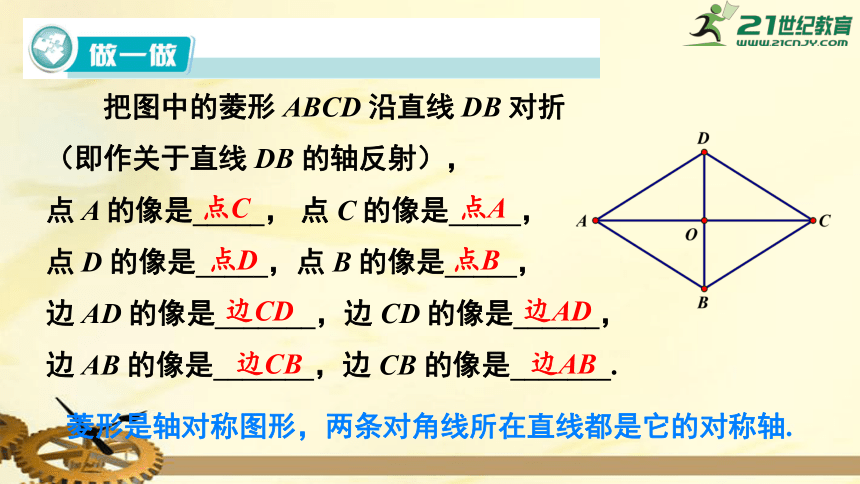
把图中的菱形
ABCD
沿直线
DB
对折
(即作关于直线
DB
的轴反射),
点
A
的像是_____,
点
C
的像是_____,
点
D
的像是_____,点
B
的像是_____,
边
AD
的像是_______,边
CD
的像是______,
边
AB
的像是_______,边
CB
的像是_______.
点C
点A
点D
点B
边CD
边AD
边CB
边AB
菱形是轴对称图形,两条对角线所在直线都是它的对称轴.
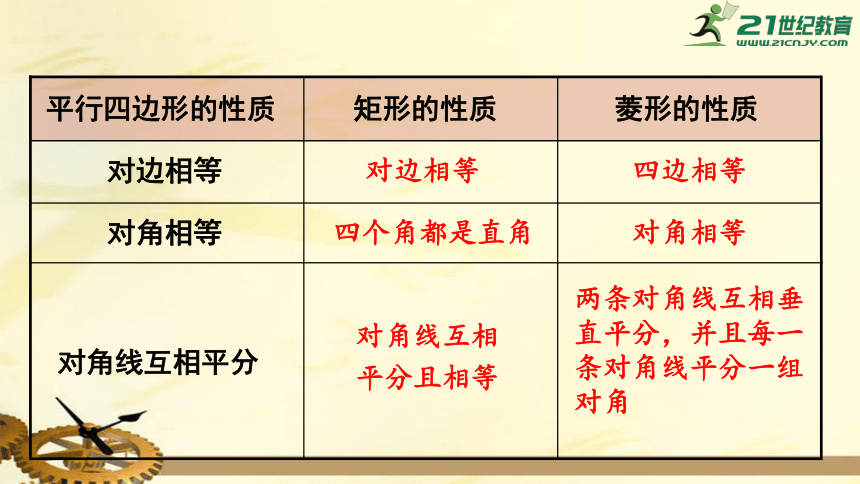
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
如图,你能利用菱形的性质说明菱形
ABCD
的
面积
吗?
又
AC⊥DB(菱形的对角线互相垂直),
如图,菱形
ABCD
的两条对角线
AC,BD
的长度分别为
4
cm,3
cm,求菱形
ABCD
的面积和周长.
所以,
因此,菱形
ABCD
的周长为4×2.5=10(cm).
解
菱形
ABCD
的面积为
在
Rt△ABO
中,
练习
【教材P67】
菱形
ABCD
的两条对角线的交点为
O.
已知
AB=5cm,OB
=
3cm.
求菱形
ABCD
的两条对角线的长度以及它的面积.
解:如右图所示.
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠AOB=60°.
∵OB=3cm,AB=5cm,
在Rt△AOB中,由勾股定理,
得AO=
故AC=2OA=8cm,BD=2OB=6cm.
故S菱形ABCD=
所以菱形ABCD的两条对角线的长度分别是8cm,6cm,它的面积为24
cm2.
解
∵
AC
是∠DAB
的平分线,
∴点
P
到
AB
的距离等于点
P
到
AD
的距离,故点
P
到
AB
的距离是
4
cm
.
2.
如图,点
P
是菱形
ABCD
的对角线
AC
上一点,
PE⊥AD
于点
E,PE
=
4
cm,求点
P
到
AB
的距离.
随堂练习
如图,
两个连接在一起的菱形的边长都是1
cm,
一只甲虫从点
A
开始按
ABCDAEFGABCD
…
的顺序沿菱形的边循环爬行,当甲虫爬行2020
cm
时停下,则它停下的位置是(
)
A.
点
F
B.
点
E
C.
点
A
D.
点
C
C
如图,
在菱形
ABCD
中,
AB
的垂直平分线
EF
交对角线
AC
于点
F
,
垂足为
E
,
连接
DF.若∠CDF
=24°,
则∠DAB
等于(
)
A.
100°
B.
104°
C.
105°
D.
110°
B
【教材P70】
如图,四边形
ABCD
是菱形,边长为
2
cm,
∠BAD
=
60°,求菱形
ABCD
的两条对角线的长度以及它的面积.
解:因为四边形ABCD是菱形,
所以OA=OC,OB=OD,AC⊥BD,AB=AD=BC=CD.
又因为∠BAD
=60°,所以△ABD
是等边三角形.
因为菱形
ABCD
的边长为2
cm,所以
BD
=2
cm
,
所以
OD
=
BD
=
×2=1
(cm).
在
Rt△AOD
中,由勾股定理,
得
所以
AC
=
2OA
=
cm.
故
S菱形ABCD
=
(cm2)
如图,在△ABC
中,AB
=AC,D,E,F
分别是
AB,BC,AC
边的中点.
(1)求证:四边形
ADEF
是菱形;
(2)若
AB
=
12
cm,求菱形
ADEF
的周长.
(1)证明:
因为
D,
E,
F,
分别是
AB,
BC,
AC
的中点,
所以
DE,
EF
是△ABC
的中位线.
所以
DE∥AC,
DE
=
AC,
EF∥AB,
EF
=
AB.
所以四边形
ADEF
是平行四边形.
又因为AB
=AC,所以
DE
=
EF.
所以
□
ADEF
是菱形
(一组邻边相等的平行四边形是菱形).
(2)解:
若AB
=12
cm,则
EF
=
AB
=6
cm.
所以菱形ADEF
的周长为
4EF
=
4×6=
24(cm).
有一组邻边相等的平行四边形叫作菱形.
课堂小结
菱形的定义:
菱形的四条边相等.
菱形的对角相等.
菱形的对角线互相垂直且平分.
菱形是中心对称图形,对角线的交点是它的对称中心.
菱形是轴对称图形,两条对角线所在直线都是它的对称轴.
菱形的性质:
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
菱形的性质
湘教版·八年级下册
上课课件
第2章
四边形
学习目标
【知识与技能】
1.理解并掌握菱形的定义及性质定理1、2;会用这些定理进行有关的论证和计算.
2.培养学生的观察能力、动手能力、自学能力、计算能力、逻辑思维能力.
3.通过运用菱形知识解决具体问题,提高分析能力和观察能力.
4.根据平行四边形与矩形、菱形的从属关系,通过画图向学生渗透集合思想.
【过程与方法】
经历探索菱形的性质和基本概念的过程,在操作、观察、分析过程中发展学生思维意识,体会几何说理的基本方法.
【情感态度】
培养学生主动探究的习惯和严密的思维意识、审判观、价值观.并在教学中渗透事物总是相互联系又是相互区别的辩证唯物主义观点.
【教学重点】
菱形的性质定理
【教学难点】
定理的证明方法及运用
新课导入
将一张矩形的纸对折,然后沿着图中的虚线剪下,猜猜看,打开是个什么图形,自己动手做一做.
观察图中的平行四边形,它们有什么特点?
它们的邻边相等.
平行四边形
菱形
一组邻边相等
菱形:有一组邻边相等的平行四边形叫作菱形.
菱形是特殊的平行四边形,思考:
①菱形的边、角、对角线具有哪些性质?
②它是中心对称图形吗?
菱形的四条边相等.
菱形的对角相等.
菱形的对角线互相平分.
菱形是中心对称图形,对角线的交点是它的对称中心.
如图,四边形
ABCD
是菱形,对角线
AC,DB
相交于点
O.
对角线
AC⊥
DB
吗?你的理由是什么?
∵
四边形
ABCD是菱形,
∴
DA
=
DC.
∴
点
D
在线段
AC
的垂直平分线上.
又点
O
为线段
AC
的中点,
∴
直线
DO(即直线
DB
)是线段
AC
的垂直平分线,
∴
AC⊥DB.
把图中的菱形
ABCD
沿直线
DB
对折
(即作关于直线
DB
的轴反射),
点
A
的像是_____,
点
C
的像是_____,
点
D
的像是_____,点
B
的像是_____,
边
AD
的像是_______,边
CD
的像是______,
边
AB
的像是_______,边
CB
的像是_______.
点C
点A
点D
点B
边CD
边AD
边CB
边AB
菱形是轴对称图形,两条对角线所在直线都是它的对称轴.
对边相等
四个角都是直角
对角线互相
平分且相等
四边相等
对角相等
两条对角线互相垂直平分,并且每一条对角线平分一组对角
平行四边形的性质
矩形的性质
菱形的性质
对边相等
对角相等
对角线互相平分
如图,你能利用菱形的性质说明菱形
ABCD
的
面积
吗?
又
AC⊥DB(菱形的对角线互相垂直),
如图,菱形
ABCD
的两条对角线
AC,BD
的长度分别为
4
cm,3
cm,求菱形
ABCD
的面积和周长.
所以,
因此,菱形
ABCD
的周长为4×2.5=10(cm).
解
菱形
ABCD
的面积为
在
Rt△ABO
中,
练习
【教材P67】
菱形
ABCD
的两条对角线的交点为
O.
已知
AB=5cm,OB
=
3cm.
求菱形
ABCD
的两条对角线的长度以及它的面积.
解:如右图所示.
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠AOB=60°.
∵OB=3cm,AB=5cm,
在Rt△AOB中,由勾股定理,
得AO=
故AC=2OA=8cm,BD=2OB=6cm.
故S菱形ABCD=
所以菱形ABCD的两条对角线的长度分别是8cm,6cm,它的面积为24
cm2.
解
∵
AC
是∠DAB
的平分线,
∴点
P
到
AB
的距离等于点
P
到
AD
的距离,故点
P
到
AB
的距离是
4
cm
.
2.
如图,点
P
是菱形
ABCD
的对角线
AC
上一点,
PE⊥AD
于点
E,PE
=
4
cm,求点
P
到
AB
的距离.
随堂练习
如图,
两个连接在一起的菱形的边长都是1
cm,
一只甲虫从点
A
开始按
ABCDAEFGABCD
…
的顺序沿菱形的边循环爬行,当甲虫爬行2020
cm
时停下,则它停下的位置是(
)
A.
点
F
B.
点
E
C.
点
A
D.
点
C
C
如图,
在菱形
ABCD
中,
AB
的垂直平分线
EF
交对角线
AC
于点
F
,
垂足为
E
,
连接
DF.若∠CDF
=24°,
则∠DAB
等于(
)
A.
100°
B.
104°
C.
105°
D.
110°
B
【教材P70】
如图,四边形
ABCD
是菱形,边长为
2
cm,
∠BAD
=
60°,求菱形
ABCD
的两条对角线的长度以及它的面积.
解:因为四边形ABCD是菱形,
所以OA=OC,OB=OD,AC⊥BD,AB=AD=BC=CD.
又因为∠BAD
=60°,所以△ABD
是等边三角形.
因为菱形
ABCD
的边长为2
cm,所以
BD
=2
cm
,
所以
OD
=
BD
=
×2=1
(cm).
在
Rt△AOD
中,由勾股定理,
得
所以
AC
=
2OA
=
cm.
故
S菱形ABCD
=
(cm2)
如图,在△ABC
中,AB
=AC,D,E,F
分别是
AB,BC,AC
边的中点.
(1)求证:四边形
ADEF
是菱形;
(2)若
AB
=
12
cm,求菱形
ADEF
的周长.
(1)证明:
因为
D,
E,
F,
分别是
AB,
BC,
AC
的中点,
所以
DE,
EF
是△ABC
的中位线.
所以
DE∥AC,
DE
=
AC,
EF∥AB,
EF
=
AB.
所以四边形
ADEF
是平行四边形.
又因为AB
=AC,所以
DE
=
EF.
所以
□
ADEF
是菱形
(一组邻边相等的平行四边形是菱形).
(2)解:
若AB
=12
cm,则
EF
=
AB
=6
cm.
所以菱形ADEF
的周长为
4EF
=
4×6=
24(cm).
有一组邻边相等的平行四边形叫作菱形.
课堂小结
菱形的定义:
菱形的四条边相等.
菱形的对角相等.
菱形的对角线互相垂直且平分.
菱形是中心对称图形,对角线的交点是它的对称中心.
菱形是轴对称图形,两条对角线所在直线都是它的对称轴.
菱形的性质:
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
