2.2简谐运动的描述— 2020-2021学年【新教材】人教版(2019)高中物理选择性必修第一册课件19张PPT
文档属性
| 名称 | 2.2简谐运动的描述— 2020-2021学年【新教材】人教版(2019)高中物理选择性必修第一册课件19张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览






文档简介
第二章 第2节 简谐运动的描述
问题导入
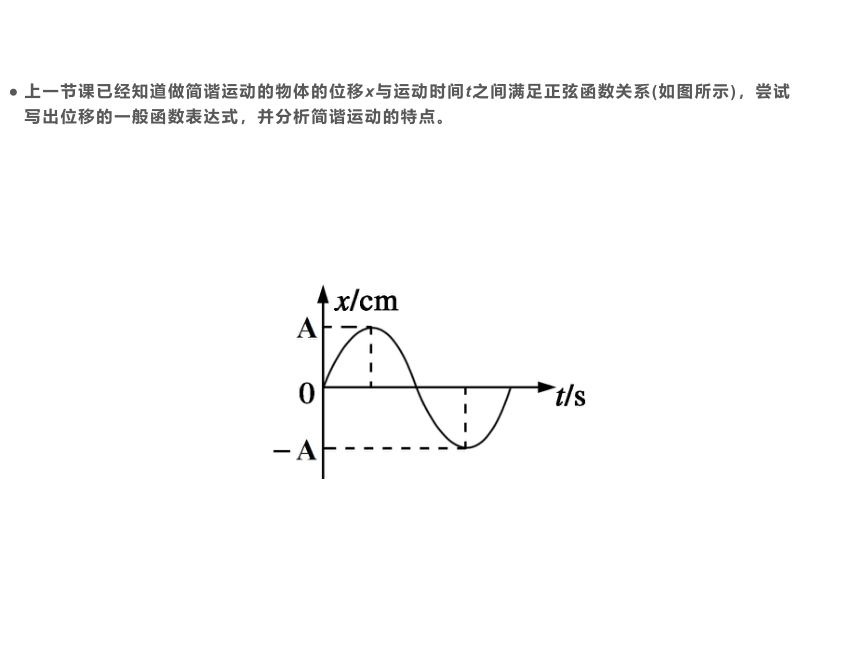
上一节课已经知道做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系(如图所示),尝试写出位移的一般函数表达式,并分析简谐运动的特点。
知识梳理
一、描述简谐运动的物理量
1.振幅
(1)定义:振动物体离开平衡位置的最大距离,叫作振动的振幅.用A表示,单位为米(m)。
(2)物理含义:振幅是表示振动幅度大小的物理量,振动物体运动范围是振幅的两倍;振幅的大小反映了振动的强弱和振动系统能量的大小。
(3)矢标性:振幅是标量。
2.全振动
(1)定义:如图振子在MM′之间振动,如果从振子向右通过O点的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。若从图中P0点向右运动开始计时,经历的一次全振动应为P0→M→P0→O→M′→O→P0.
(2)特征:
①当完成一次全振动时,振动的位移(x)、加速度(a)、速度(v)三者第一次同时恢复到与初始状态相同。
②从任意一点开始计时,物体完成一次全振动的时间总是相同的。
3.周期(T)和频率(f)
4.圆频率(ω)
5.相位和相位差
(1)相位:当(ωt+φ)确定时,x=Asin(ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫作相位。Φ是t=0时的相位,称为初相位或初相。
(2)相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
讨论:Δφ=(ωt+φ1)-(ωt+φ2)=φ1-φ2 (-π≤Δφ≤π)
①Δφ=0,表明两振动步调完全相同,称为同相。
②Δφ=π或-π,表明两振动步调完全相反,称为反相。
③Δφ>0,表示振动1的相位比振动2超前Δφ。
④Δφ<0,表示振动1的相位比振动2滞后Δφ。
★辨析:振幅与位移、路程、周期的关系
(1)振幅与位移:振动中的位移是矢量,随时间做周期性的变化;振幅是标量,在同一简谐运动中振幅大小是确定的,等于最大位移的大小。
(2)振幅与路程:振动中的路程是标量,随时间不断增大的。其中物体从任意一点开始,一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅。(个周期内的路程不一定为1倍振幅,除非从两个端点或平衡位置开始计时)
(3)振幅与周期:周期(或频率)由振动系统本身的因素决定,是固定的。振幅与系统的能量有关,同一振动系统能量越大,振幅越大,周期(或频率)不变。
二、简谐运动的表达式
1.表达式:
x=Asin或x=Asin(t+φ)
2.表达式中各量的意义
(1)“A”表示简谐运动的“振幅”.
(2)ω是一个与频率成正比的物理量叫简谐运动的圆频率.
(3)“T”表示简谐运动的周期,“f”表示简谐运动的频率,
它们之间的关系为
(4)“t+φ”或“2πft+φ”表示简谐运动的相位.
(5)“φ”表示简谐运动的初相位,简称初相.
1.振幅就是振子的最大位移. (×)
2.从任一个位置出发又回到这个位置所用的最短时间就是一个周期.(×)
3.振动物体的周期越大,表示振动的越快. (×)
4.简谐运动的位移表达式与计时时刻物体所在位置无关. (×)
5.一个物体运动时其相位变化2π,就意味着完成一次全振动. (√)
6.简谐运动的表达式x=Asin(ωt+φ)中,ωt+φ的单位是弧度. (√)
判一判
重点突破
[例1]如图所示,弹簧振子以O为平衡位置在BC间做简谐运动,则( )
A.从B→O→C为一次全振动
B.从O→B→O→C为一次全振动
C.从C→O→B→O→C为一次全振动
D.从D→C→O→B→O为一次全振动
任务一:描述简谐运动的物理量
答案:C
[例2]如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动,且AB=20 cm,振子首次由A到B的时间为0.1 s,求:
(1)振子振动的振幅、周期和频率;
(2)振子由A到O的时间;
(3)振子在5 s内通过的路程及位移大小。
答案: (1)10 cm 0.2 s 5 Hz (2)0.05 s (3)1 000 cm 10 cm
[变式训练1]如图,弹簧振子的平衡位置为O点,在B、C两点之间做简谐运动。B、C相距20cm。小球经过B点时开始计时,经过0.5s首次到达C点。
(1)写出小球的运动表达式并画出小球在第一个周期内的x?t图像。
(2)求5s内小球通过的路程及5s末小球的位移。
答案: (1) 5 Hz (2)2m 0.1m
[变式训练2]一质点做简谐运动,其相对平衡位置的位移x与时间t的关系如图所示,由图可知( )
A.质点振动的频率为1.6 Hz
B.质点振动的振幅为4.0 cm
C.在0.3 s和0.5 s两时刻,质点的速度方向相同
D.在0.3 s和0.5 s两时刻,质点的加速度方向相同
答案: C
任务二:简谐运动的表达式
答案: CDE
[变式训练3]一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程,并画出相应的振动图象.
谢谢观看!
问题导入
上一节课已经知道做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系(如图所示),尝试写出位移的一般函数表达式,并分析简谐运动的特点。
知识梳理
一、描述简谐运动的物理量
1.振幅
(1)定义:振动物体离开平衡位置的最大距离,叫作振动的振幅.用A表示,单位为米(m)。
(2)物理含义:振幅是表示振动幅度大小的物理量,振动物体运动范围是振幅的两倍;振幅的大小反映了振动的强弱和振动系统能量的大小。
(3)矢标性:振幅是标量。
2.全振动
(1)定义:如图振子在MM′之间振动,如果从振子向右通过O点的时刻开始计时,它将运动到M,然后向左回到O,又继续向左运动到达M′,之后又向右回到O。这样一个完整的振动过程称为一次全振动。若从图中P0点向右运动开始计时,经历的一次全振动应为P0→M→P0→O→M′→O→P0.
(2)特征:
①当完成一次全振动时,振动的位移(x)、加速度(a)、速度(v)三者第一次同时恢复到与初始状态相同。
②从任意一点开始计时,物体完成一次全振动的时间总是相同的。
3.周期(T)和频率(f)
4.圆频率(ω)
5.相位和相位差
(1)相位:当(ωt+φ)确定时,x=Asin(ωt+φ)的函数值也就确定了,即物体做简谐运动的位置状态就确定了。物理学中把(ωt+φ)叫作相位。Φ是t=0时的相位,称为初相位或初相。
(2)相位差:指两个简谐运动的相位之差,可以反映出两个简谐运动的步调差异,经常用到的是两个具有相同频率的简谐运动的相位差。
讨论:Δφ=(ωt+φ1)-(ωt+φ2)=φ1-φ2 (-π≤Δφ≤π)
①Δφ=0,表明两振动步调完全相同,称为同相。
②Δφ=π或-π,表明两振动步调完全相反,称为反相。
③Δφ>0,表示振动1的相位比振动2超前Δφ。
④Δφ<0,表示振动1的相位比振动2滞后Δφ。
★辨析:振幅与位移、路程、周期的关系
(1)振幅与位移:振动中的位移是矢量,随时间做周期性的变化;振幅是标量,在同一简谐运动中振幅大小是确定的,等于最大位移的大小。
(2)振幅与路程:振动中的路程是标量,随时间不断增大的。其中物体从任意一点开始,一个周期内的路程为4倍振幅,半个周期内的路程为2倍振幅。(个周期内的路程不一定为1倍振幅,除非从两个端点或平衡位置开始计时)
(3)振幅与周期:周期(或频率)由振动系统本身的因素决定,是固定的。振幅与系统的能量有关,同一振动系统能量越大,振幅越大,周期(或频率)不变。
二、简谐运动的表达式
1.表达式:
x=Asin或x=Asin(t+φ)
2.表达式中各量的意义
(1)“A”表示简谐运动的“振幅”.
(2)ω是一个与频率成正比的物理量叫简谐运动的圆频率.
(3)“T”表示简谐运动的周期,“f”表示简谐运动的频率,
它们之间的关系为
(4)“t+φ”或“2πft+φ”表示简谐运动的相位.
(5)“φ”表示简谐运动的初相位,简称初相.
1.振幅就是振子的最大位移. (×)
2.从任一个位置出发又回到这个位置所用的最短时间就是一个周期.(×)
3.振动物体的周期越大,表示振动的越快. (×)
4.简谐运动的位移表达式与计时时刻物体所在位置无关. (×)
5.一个物体运动时其相位变化2π,就意味着完成一次全振动. (√)
6.简谐运动的表达式x=Asin(ωt+φ)中,ωt+φ的单位是弧度. (√)
判一判
重点突破
[例1]如图所示,弹簧振子以O为平衡位置在BC间做简谐运动,则( )
A.从B→O→C为一次全振动
B.从O→B→O→C为一次全振动
C.从C→O→B→O→C为一次全振动
D.从D→C→O→B→O为一次全振动
任务一:描述简谐运动的物理量
答案:C
[例2]如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动,且AB=20 cm,振子首次由A到B的时间为0.1 s,求:
(1)振子振动的振幅、周期和频率;
(2)振子由A到O的时间;
(3)振子在5 s内通过的路程及位移大小。
答案: (1)10 cm 0.2 s 5 Hz (2)0.05 s (3)1 000 cm 10 cm
[变式训练1]如图,弹簧振子的平衡位置为O点,在B、C两点之间做简谐运动。B、C相距20cm。小球经过B点时开始计时,经过0.5s首次到达C点。
(1)写出小球的运动表达式并画出小球在第一个周期内的x?t图像。
(2)求5s内小球通过的路程及5s末小球的位移。
答案: (1) 5 Hz (2)2m 0.1m
[变式训练2]一质点做简谐运动,其相对平衡位置的位移x与时间t的关系如图所示,由图可知( )
A.质点振动的频率为1.6 Hz
B.质点振动的振幅为4.0 cm
C.在0.3 s和0.5 s两时刻,质点的速度方向相同
D.在0.3 s和0.5 s两时刻,质点的加速度方向相同
答案: C
任务二:简谐运动的表达式
答案: CDE
[变式训练3]一物体沿x轴做简谐运动,振幅为8 cm,频率为0.5 Hz,在t=0时,位移是4 cm,且向x轴负方向运动,试写出用正弦函数表示的振动方程,并画出相应的振动图象.
谢谢观看!
