人教版五年级下册数学课件 运用优化策略解决问题(17页PPT)
文档属性
| 名称 | 人教版五年级下册数学课件 运用优化策略解决问题(17页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览


文档简介
人教版数学五年级下册
8
数学广角——找次品
第2课时 运用优化策略解决问题
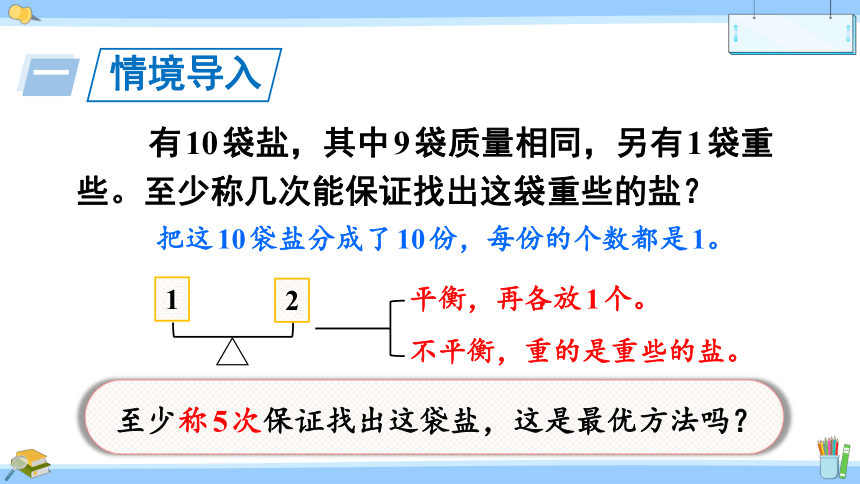
有10袋盐,其中9袋质量相同,另有1袋重些。至少称几次能保证找出这袋重些的盐?
1
2
平衡,再各放1个。
不平衡,重的是重些的盐。
把这10袋盐分成了10份,每份的个数都是1。
至少称5次保证找出这袋盐,这是最优方法吗?
二 新课探究
(教科书第112页例2)
2
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
肯定能找出次品的最少次数。
你们打算怎样表示找次品的过程?
动手小实验
1
2
3
4
5
6
7
8
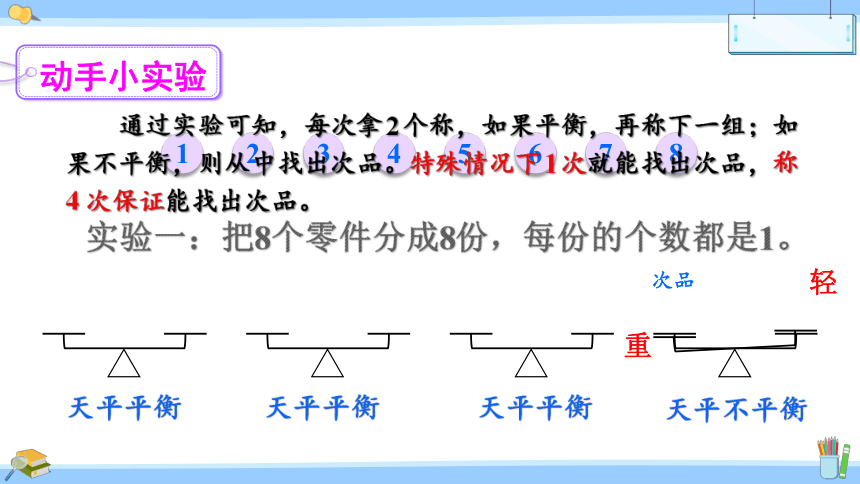
天平平衡
天平平衡
天平平衡
天平不平衡
重
轻
次品
通过实验可知,每次拿2个称,如果平衡,再称下一组;如果不平衡,则从中找出次品。特殊情况下1次就能找出次品,称4次保证能找出次品。
1
2
3
4
5
6
7
8
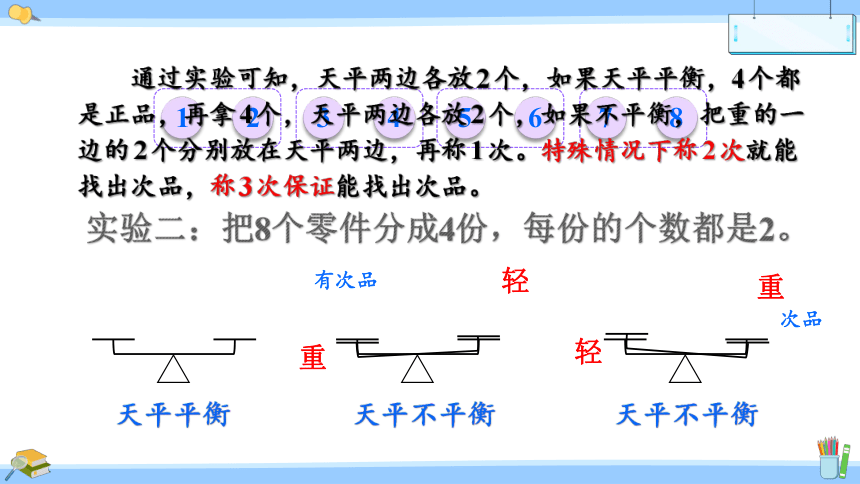
天平平衡
天平不平衡
天平不平衡
轻
重
次品
重
轻
有次品
通过实验可知,天平两边各放2个,如果天平平衡,4个都是正品,再拿4个,天平两边各放2个,如果不平衡,把重的一边的2个分别放在天平两边,再称1次。特殊情况下称2次就能找出次品,称3次保证能找出次品。
1
2
3
4
5
6
7
8
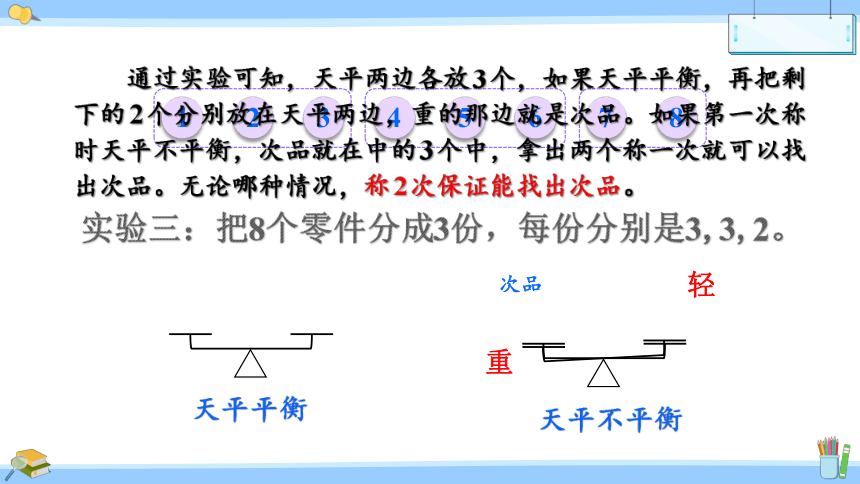
天平平衡
天平不平衡
重
轻
次品
通过实验可知,天平两边各放3个,如果天平平衡,再把剩下的2个分别放在天平两边,重的那边就是次品。如果第一次称时天平不平衡,次品就在中的3个中,拿出两个称一次就可以找出次品。无论哪种情况,称2次保证能找出次品。
1
2
3
4
5
6
7
8
天平不平衡
天平不平衡
轻
重
次品
有次品
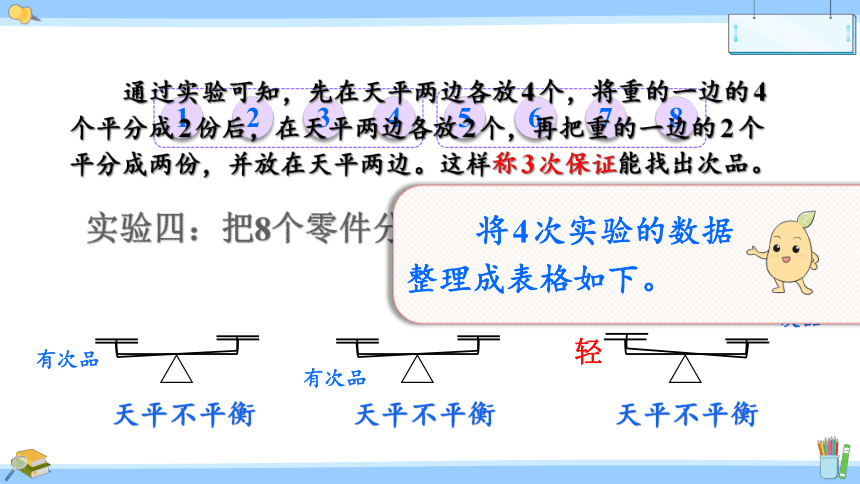
通过实验可知,先在天平两边各放4个,将重的一边的4个平分成2份后,在天平两边各放2个,再把重的一边的2个平分成两份,并放在天平两边。这样称3次保证能找出次品。
天平不平衡
有次品
将4次实验的数据整理成表格如下。
每次每边放的个数
分成的份数
至少要称的次数
1
8份(1,1,1,1,1,1,1,1)
4
2
4份(2,2,2,2)
3
3
3份(3,3,2)
2
4
2份(4,4)
3
根据实验的观察以及整理的表格可以得出,将零件分成3份,称的次数最少。
如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?那10个、11个零件呢?你能发现什么?
9
(3,3,3)
两边各放3个
平衡,再称剩下的3个
找出次品
不平衡,再称重的那边3个
找出次品
需要称 次。
2
10
(3,3,4)
两边各放3个
平衡:
不平衡:
4
(1,1,2)
称3次
3
(1,1,1)
称2次
11
(4,4,3)
两边各放4个
平衡:
不平衡:
3
(1,1,1)
称2次
4
(1,1,2)
称3次
我发现:尽可能将零件平均分成3份,如果不能平均分成3份,则使多的一份与少的一份个数相差1,这样找出次品需要称的次数最少。
填空题。
有4颗珍珠,其中有1颗较轻,是假珍珠,其他3颗质量相同用天平至少称( )次就能保证找出这颗假珍珠。
2. 有13瓶药,其中有1瓶少了几片,其余12瓶质量相同,
用天平至少称( )次能保证找出比较轻的这瓶药。
2
3
有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
28
(9,9,10)
两边各放9个
平衡:
不平衡:
10
(3,3,4)
称4次
9
(3,3,3)
称3次
至少需要称 次。
4
有9个外形完全相同的羽毛球,其中8个是正品,1个是次品,且次品稍轻一些。如果用天平称,至少称几次就一定能找出这个次品?会不会出现一次就把次品找出来的情况?
至少称2次。如果天平每边放4个羽毛球,天平平衡,则剩下的那个为次品,即会出现一次就把次品找出来的情况。
有10袋零件,每袋都有十几个,其中1袋中的全部零件都是次品。已知每个次品零件都重9g,比合格品零件轻1g,你能只称一次就找出这袋次品零件吗?
将10袋零件分别编号为①、②、③、…、⑨、⑩,从袋中取出1个零件,从②袋中取出2个零件,……,从⑩袋中取出10个零件,则总质量比550g轻几克,第几袋就是次品。
把待测物品分成3份,要尽量分得平均,不能够平均分的,也应该使多的一份与少的一份只相差1。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
8
数学广角——找次品
第2课时 运用优化策略解决问题
有10袋盐,其中9袋质量相同,另有1袋重些。至少称几次能保证找出这袋重些的盐?
1
2
平衡,再各放1个。
不平衡,重的是重些的盐。
把这10袋盐分成了10份,每份的个数都是1。
至少称5次保证找出这袋盐,这是最优方法吗?
二 新课探究
(教科书第112页例2)
2
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
肯定能找出次品的最少次数。
你们打算怎样表示找次品的过程?
动手小实验
1
2
3
4
5
6
7
8
天平平衡
天平平衡
天平平衡
天平不平衡
重
轻
次品
通过实验可知,每次拿2个称,如果平衡,再称下一组;如果不平衡,则从中找出次品。特殊情况下1次就能找出次品,称4次保证能找出次品。
1
2
3
4
5
6
7
8
天平平衡
天平不平衡
天平不平衡
轻
重
次品
重
轻
有次品
通过实验可知,天平两边各放2个,如果天平平衡,4个都是正品,再拿4个,天平两边各放2个,如果不平衡,把重的一边的2个分别放在天平两边,再称1次。特殊情况下称2次就能找出次品,称3次保证能找出次品。
1
2
3
4
5
6
7
8
天平平衡
天平不平衡
重
轻
次品
通过实验可知,天平两边各放3个,如果天平平衡,再把剩下的2个分别放在天平两边,重的那边就是次品。如果第一次称时天平不平衡,次品就在中的3个中,拿出两个称一次就可以找出次品。无论哪种情况,称2次保证能找出次品。
1
2
3
4
5
6
7
8
天平不平衡
天平不平衡
轻
重
次品
有次品
通过实验可知,先在天平两边各放4个,将重的一边的4个平分成2份后,在天平两边各放2个,再把重的一边的2个平分成两份,并放在天平两边。这样称3次保证能找出次品。
天平不平衡
有次品
将4次实验的数据整理成表格如下。
每次每边放的个数
分成的份数
至少要称的次数
1
8份(1,1,1,1,1,1,1,1)
4
2
4份(2,2,2,2)
3
3
3份(3,3,2)
2
4
2份(4,4)
3
根据实验的观察以及整理的表格可以得出,将零件分成3份,称的次数最少。
如果9个零件中有1个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?那10个、11个零件呢?你能发现什么?
9
(3,3,3)
两边各放3个
平衡,再称剩下的3个
找出次品
不平衡,再称重的那边3个
找出次品
需要称 次。
2
10
(3,3,4)
两边各放3个
平衡:
不平衡:
4
(1,1,2)
称3次
3
(1,1,1)
称2次
11
(4,4,3)
两边各放4个
平衡:
不平衡:
3
(1,1,1)
称2次
4
(1,1,2)
称3次
我发现:尽可能将零件平均分成3份,如果不能平均分成3份,则使多的一份与少的一份个数相差1,这样找出次品需要称的次数最少。
填空题。
有4颗珍珠,其中有1颗较轻,是假珍珠,其他3颗质量相同用天平至少称( )次就能保证找出这颗假珍珠。
2. 有13瓶药,其中有1瓶少了几片,其余12瓶质量相同,
用天平至少称( )次能保证找出比较轻的这瓶药。
2
3
有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
28
(9,9,10)
两边各放9个
平衡:
不平衡:
10
(3,3,4)
称4次
9
(3,3,3)
称3次
至少需要称 次。
4
有9个外形完全相同的羽毛球,其中8个是正品,1个是次品,且次品稍轻一些。如果用天平称,至少称几次就一定能找出这个次品?会不会出现一次就把次品找出来的情况?
至少称2次。如果天平每边放4个羽毛球,天平平衡,则剩下的那个为次品,即会出现一次就把次品找出来的情况。
有10袋零件,每袋都有十几个,其中1袋中的全部零件都是次品。已知每个次品零件都重9g,比合格品零件轻1g,你能只称一次就找出这袋次品零件吗?
将10袋零件分别编号为①、②、③、…、⑨、⑩,从袋中取出1个零件,从②袋中取出2个零件,……,从⑩袋中取出10个零件,则总质量比550g轻几克,第几袋就是次品。
把待测物品分成3份,要尽量分得平均,不能够平均分的,也应该使多的一份与少的一份只相差1。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
