2.2 圆心角、圆周角( 第2课时) 圆周角(2) 课件(共21张PPT)
文档属性
| 名称 | 2.2 圆心角、圆周角( 第2课时) 圆周角(2) 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 07:42:11 | ||
图片预览


文档简介
(共21张PPT)
圆周角(2)
第2章
圆
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.巩固圆周角概念及圆周角定理.
2.掌握圆周角定理的推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
3.圆内接四边形的对角互补.
【过程与方法】
在探索圆周角定理的推论中,培养学生观察、比较、归纳、概括的能力.
【情感态度】
在探索过程中感受成功,建立自信,体验数学学习活动充满着探索与创造,交流与合作的乐趣.
【教学重点】
对直径所对的圆周角是直角及90°的圆周角所对的弦是直径这些性质的理解.
【教学难点】
对圆周角定理推论的灵活运用是难点.
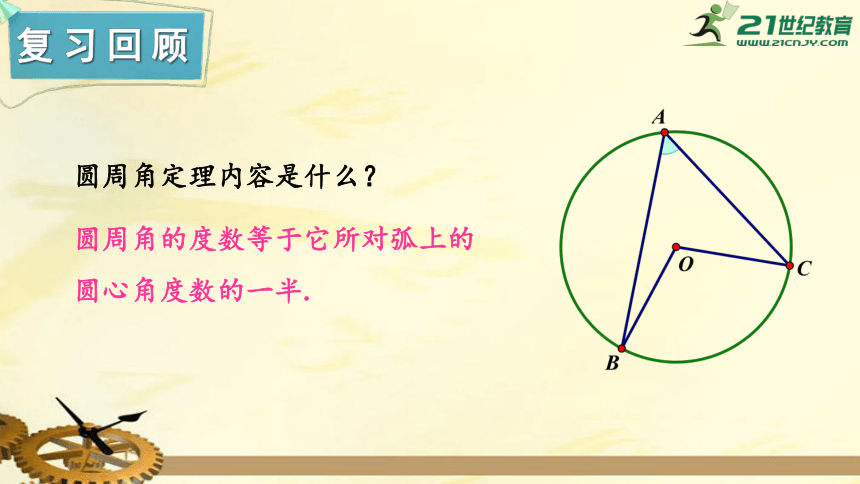
复习回顾
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理内容是什么?
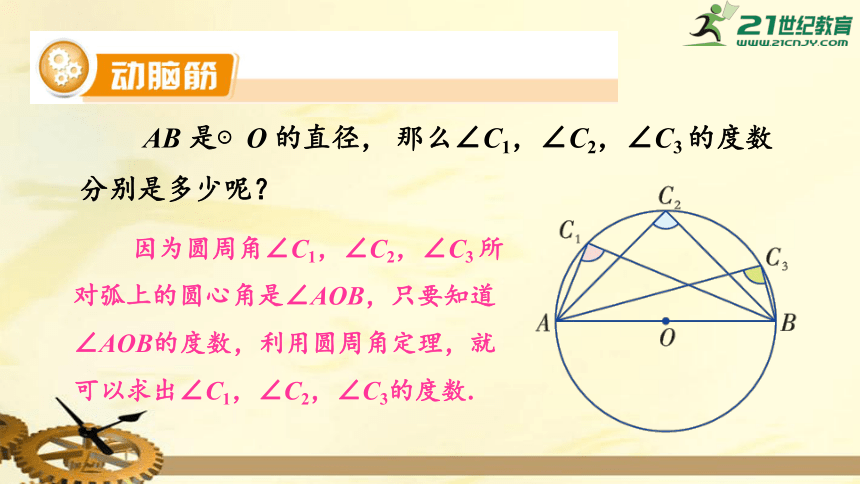
AB
是⊙O
的直径,
那么∠C1,∠C2,∠C3
的度数分别是多少呢?
因为圆周角∠C1,∠C2,∠C3
所对弧上的圆心角是∠AOB,只要知道∠AOB的度数,利用圆周角定理,就可以求出∠C1,∠C2,∠C3的度数.
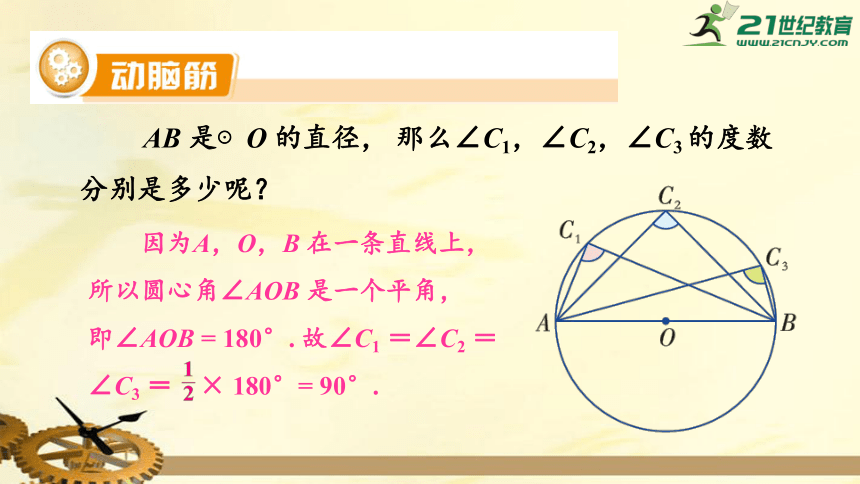
AB
是⊙O
的直径,
那么∠C1,∠C2,∠C3
的度数分别是多少呢?
因为A,O,B
在一条直线上,
所以圆心角∠AOB
是一个平角,
即∠AOB
=
180°.
故∠C1
=∠C2
=∠C3
=
×
180°=
90°.
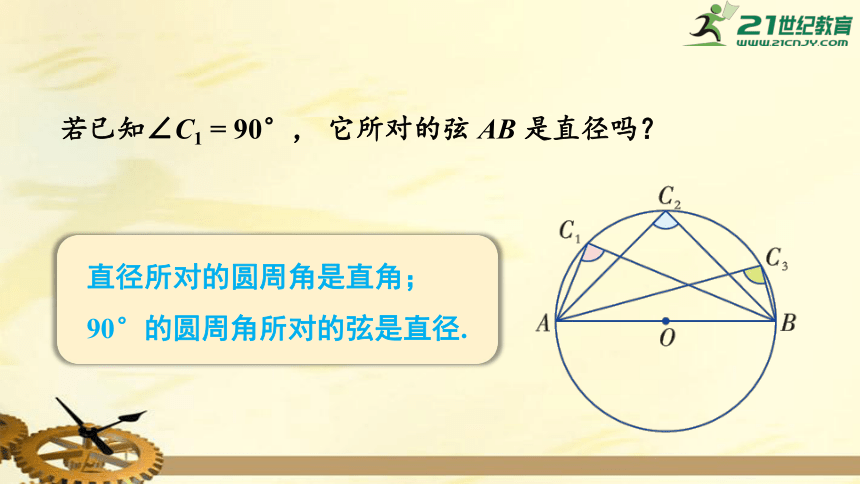
若已知∠C1
=
90°,
它所对的弦
AB
是直径吗?
直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
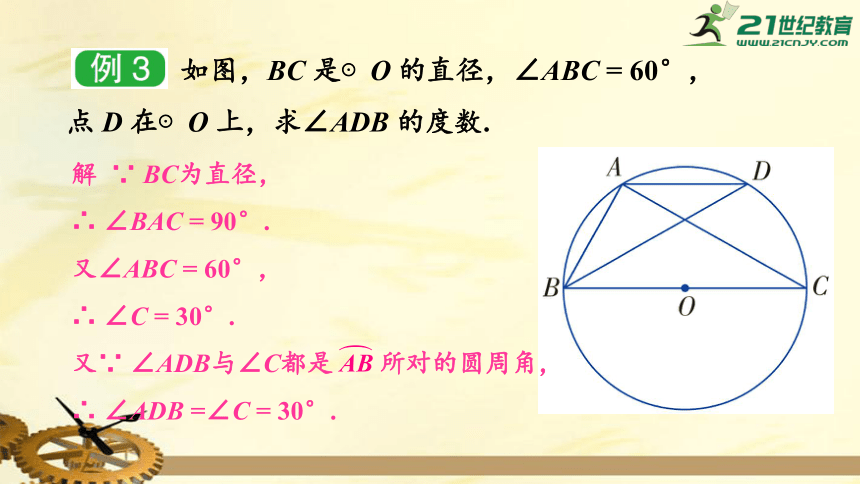
如图,BC
是⊙O
的直径,∠ABC
=
60°,
点
D
在⊙O
上,求∠ADB
的度数.
解
∵
BC为直径,
∴
∠BAC
=
90°.
又∠ABC
=
60°,
∴
∠C
=
30°.
又∵
∠ADB与∠C都是
所对的圆周角,
∴
∠ADB
=∠C
=
30°.
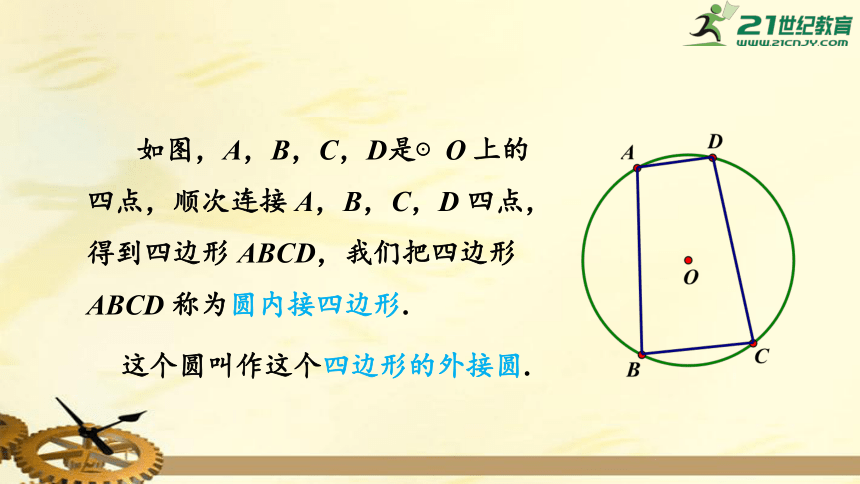
如图,A,B,C,D是⊙O
上的四点,顺次连接
A,B,C,D
四点,
得到四边形
ABCD,我们把四边形ABCD
称为圆内接四边形.
这个圆叫作这个四边形的外接圆.
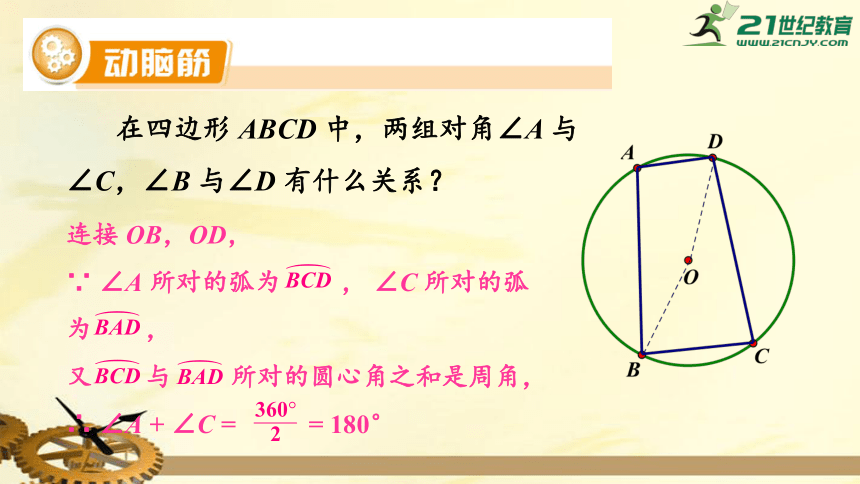
在四边形
ABCD
中,两组对角∠A
与∠C,∠B
与∠D
有什么关系?
连接
OB,OD,
∵
∠A
所对的弧为
,
∠C
所对的弧为
,
又
与
所对的圆心角之和是周角,
∴
∠A
+
∠C
=
=
180°
圆内接四边形的对角互补.
结论:
如图,四边形ABCD
为
⊙O
的内接四边形,已知∠BOD
为
100°,求∠BAD
及∠BCD
的度数.
解
∵
圆心角∠BOD与圆周角∠BAD所对的弧为
,
∠BOD
=
100°,
∴
∠BAD
=
∠BOD
=
×100°=
50°.
∵
∠BCD
+∠BAD
=
180°,
∴
∠BCD
=
180°-∠BAD
=
180°-
50°=
130°.
1.
如图,在⊙O中,AB
是直径,C,D
是圆上两点,且
AC
=
AD.
求证:BC
=
BD.
练习
解
∵
AC
=
AD,
∴
∠ABC
=
∠ABD
.
又∵
∠C
=
∠D
=
90°,
∴∠CAB
=
∠DAB
,
∴
BC
=
BD.
2.
怎样运用三角板画出如图所示的圆形件表面上的直径,
并标出圆心,试说明画法的理由.
3.
如图,圆内接四边形
ABCD
的外角
∠DCE
=
85°,求∠A
的度数.
解
∵∠A
+∠BCD
=
180°,
∠BCD
+
∠DCE
=
180°,
∴∠A
=∠DCE
=
85°.
随堂练习
1.
如图,
AB
是☉O
的直径
,
C
,
D
是☉O
上位于
AB
异侧的两点.下列四个角中,
一定与∠ACD
互余的是(
)
A.
∠ADC
B.
∠ABD
C.
∠BAC
D.
∠BAD
D
2.
如图,四边形
ABCD
内接于☉O,
AB
经过圆心,
∠B=
3∠BAC
,
则∠ADC
等于(
)
A.
100°
B.
112.5°
C.
120°
D.
135°
B
3.
(分类讨论题)如图,
A
,
B
,
C
是☉O
上的三点
,
且四
边形
OABC
是菱形.若点
D
是圆上异于
A
,
B
,
C
的
另一点
,
则∠ADC
的度数是____________.
60°或120°
课堂小结
①直径所对的圆周角是直角,90°的圆周角所对的弦是直径;
②圆内接四边形定义及性质;
③关于圆周角定理运用中,遇到直径,常构造直角三角形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
圆周角(2)
第2章
圆
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.巩固圆周角概念及圆周角定理.
2.掌握圆周角定理的推论:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
3.圆内接四边形的对角互补.
【过程与方法】
在探索圆周角定理的推论中,培养学生观察、比较、归纳、概括的能力.
【情感态度】
在探索过程中感受成功,建立自信,体验数学学习活动充满着探索与创造,交流与合作的乐趣.
【教学重点】
对直径所对的圆周角是直角及90°的圆周角所对的弦是直径这些性质的理解.
【教学难点】
对圆周角定理推论的灵活运用是难点.
复习回顾
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理内容是什么?
AB
是⊙O
的直径,
那么∠C1,∠C2,∠C3
的度数分别是多少呢?
因为圆周角∠C1,∠C2,∠C3
所对弧上的圆心角是∠AOB,只要知道∠AOB的度数,利用圆周角定理,就可以求出∠C1,∠C2,∠C3的度数.
AB
是⊙O
的直径,
那么∠C1,∠C2,∠C3
的度数分别是多少呢?
因为A,O,B
在一条直线上,
所以圆心角∠AOB
是一个平角,
即∠AOB
=
180°.
故∠C1
=∠C2
=∠C3
=
×
180°=
90°.
若已知∠C1
=
90°,
它所对的弦
AB
是直径吗?
直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
如图,BC
是⊙O
的直径,∠ABC
=
60°,
点
D
在⊙O
上,求∠ADB
的度数.
解
∵
BC为直径,
∴
∠BAC
=
90°.
又∠ABC
=
60°,
∴
∠C
=
30°.
又∵
∠ADB与∠C都是
所对的圆周角,
∴
∠ADB
=∠C
=
30°.
如图,A,B,C,D是⊙O
上的四点,顺次连接
A,B,C,D
四点,
得到四边形
ABCD,我们把四边形ABCD
称为圆内接四边形.
这个圆叫作这个四边形的外接圆.
在四边形
ABCD
中,两组对角∠A
与∠C,∠B
与∠D
有什么关系?
连接
OB,OD,
∵
∠A
所对的弧为
,
∠C
所对的弧为
,
又
与
所对的圆心角之和是周角,
∴
∠A
+
∠C
=
=
180°
圆内接四边形的对角互补.
结论:
如图,四边形ABCD
为
⊙O
的内接四边形,已知∠BOD
为
100°,求∠BAD
及∠BCD
的度数.
解
∵
圆心角∠BOD与圆周角∠BAD所对的弧为
,
∠BOD
=
100°,
∴
∠BAD
=
∠BOD
=
×100°=
50°.
∵
∠BCD
+∠BAD
=
180°,
∴
∠BCD
=
180°-∠BAD
=
180°-
50°=
130°.
1.
如图,在⊙O中,AB
是直径,C,D
是圆上两点,且
AC
=
AD.
求证:BC
=
BD.
练习
解
∵
AC
=
AD,
∴
∠ABC
=
∠ABD
.
又∵
∠C
=
∠D
=
90°,
∴∠CAB
=
∠DAB
,
∴
BC
=
BD.
2.
怎样运用三角板画出如图所示的圆形件表面上的直径,
并标出圆心,试说明画法的理由.
3.
如图,圆内接四边形
ABCD
的外角
∠DCE
=
85°,求∠A
的度数.
解
∵∠A
+∠BCD
=
180°,
∠BCD
+
∠DCE
=
180°,
∴∠A
=∠DCE
=
85°.
随堂练习
1.
如图,
AB
是☉O
的直径
,
C
,
D
是☉O
上位于
AB
异侧的两点.下列四个角中,
一定与∠ACD
互余的是(
)
A.
∠ADC
B.
∠ABD
C.
∠BAC
D.
∠BAD
D
2.
如图,四边形
ABCD
内接于☉O,
AB
经过圆心,
∠B=
3∠BAC
,
则∠ADC
等于(
)
A.
100°
B.
112.5°
C.
120°
D.
135°
B
3.
(分类讨论题)如图,
A
,
B
,
C
是☉O
上的三点
,
且四
边形
OABC
是菱形.若点
D
是圆上异于
A
,
B
,
C
的
另一点
,
则∠ADC
的度数是____________.
60°或120°
课堂小结
①直径所对的圆周角是直角,90°的圆周角所对的弦是直径;
②圆内接四边形定义及性质;
③关于圆周角定理运用中,遇到直径,常构造直角三角形.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
