9.1.1正弦定理 课件(共58张PPT)2020-2021学年高一数学人教B版(2019)必修第四册第九章
文档属性
| 名称 | 9.1.1正弦定理 课件(共58张PPT)2020-2021学年高一数学人教B版(2019)必修第四册第九章 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览









文档简介
9.1.1 正弦定理
课标阐释
思维脉络
1.通过对任意三角形边长和角度的关系的探索,掌握正弦定理的内容及其证明方法.
2.能运用正弦定理与三角形的内角和定理解决简单的解三角形问题.
3.熟记并能应用正弦定理的有关变形公式解决三角形中的问题.
4.能根据条件,判断三角形解的个数.
5.能利用正弦定理、三角形面积公式解决较为复杂的三角形问题.
激趣诱思
知识点拨
在我国古代就有嫦娥奔月的神话故事.明月高悬,我们仰望星空,会有无限遐想,有人不禁会问,遥不可及的月亮离地球究竟有多远呢?其实,早在1671年,两位法国科学家就测出了地球与月球之间的距离约为385 400千米,如左侧的图所示.你知道他们是怎样测量出来的吗?提示:将左侧的图简化为右侧的图,再思考一下吧。
激趣诱思
知识点拨
知识点一:三角形的面积
常用三角形面积公式
激趣诱思
知识点拨
微练习
答案:60°或120°
激趣诱思
知识点拨
知识点二:正弦定理
1.正弦定理的表示
文字语言
在一个三角形中,各边的长和它所对角的正弦的比相等
符号语言
在△ABC中,角A,B,C所对的边分别为a,b,c,
则
激趣诱思
知识点拨
2.正弦定理的变形
=2R(R为△ABC外接圆的半径).
(1)sin A∶sin B∶sin C=a∶b∶c;
激趣诱思
知识点拨
名师点析1.使用正弦定理的前提是在同一三角形中.
2.正弦定理的主要功能是实现三角形中边角关系的转化.
3.由正弦定理可知三角形中每两边及对应角的正弦为知三求一的关系.
激趣诱思
知识点拨
微思考
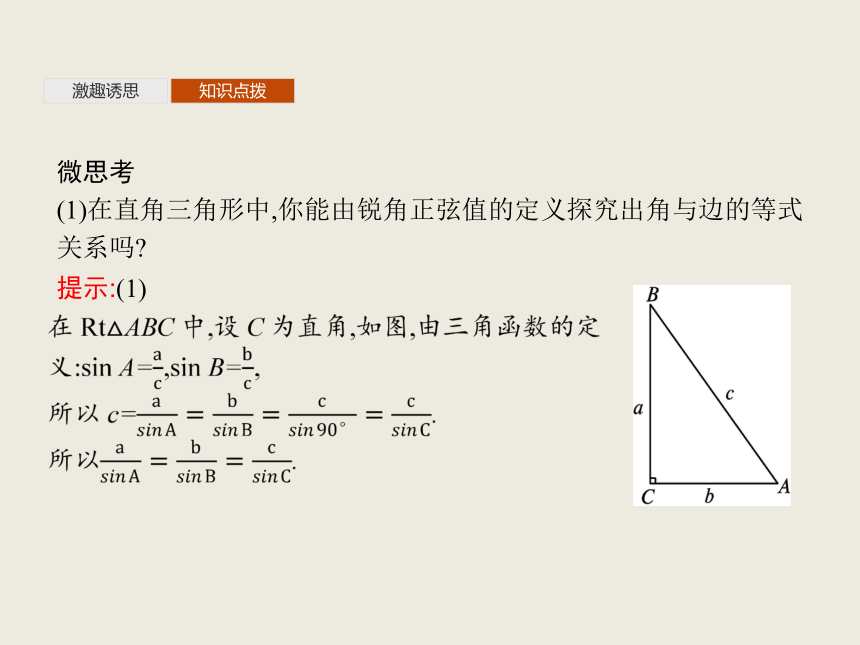
(1)在直角三角形中,你能由锐角正弦值的定义探究出角与边的等式关系吗?
提示:(1)
激趣诱思
知识点拨
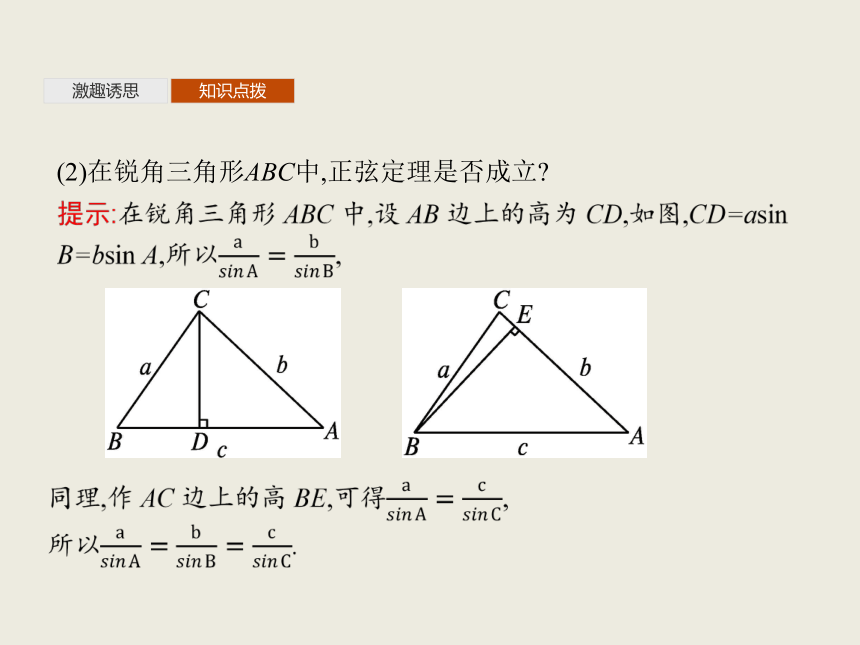
(2)在锐角三角形ABC中,正弦定理是否成立?
激趣诱思
知识点拨
(3)在钝角三角形ABC中,正弦定理是否成立?
提示:在钝角三角形ABC中,设C为钝角,如图,过点B作BD⊥AC交AC的延长线于点D,则BD=asin(π-C)=asin C,BD=csin A,
故有asin C=csin A,
激趣诱思
知识点拨
激趣诱思
知识点拨
(5)能否利用三角形的面积公式推出正弦定理?
激趣诱思
知识点拨
知识点三:解三角形
1.习惯上,我们把三角形的3个角与3条边都称为三角形的元素.已知三角形的若干元素求其他元素一般称为解三角形.
2.利用正弦定理可以解决以下两类有关解三角形的问题:
(1)已知两角和任意一边求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角,从而进一步求出其他的边和角.
激趣诱思
知识点拨
名师点析1.应用正弦定理,要明确角化边(或边化角)的方法,对三角形有几个解必须清楚明了,防止出现漏解或增解.
2.求角问题注意大边对大角性质的应用,以便判断解的个数.
激趣诱思
知识点拨
微练习1
△ABC的内角A,B,C的对边分别为a,b,c.若
答案:D
激趣诱思
知识点拨
微练习2
答案:45°
激趣诱思
知识点拨
知识点四:对三角形解的个数的判断
已知三角形的两角和任意一边,求另两边和另一角,此时三角形被唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.现以已知a,b和A解三角形为例予以说明:
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
锐
角
①a=bsin A;
②a≥b
一解
③bsin A 两解
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
锐
角
a 无解
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
钝
角
或
直
角
a>b
一解
④a≤b
无解
激趣诱思
知识点拨
微思考
在△ABC中,若A>B,一定有sin A>sin B吗?反之,若sin A>sin B,一定有A>B吗?
提示:由A>B,得a>b,
所以2Rsin A>2Rsin B,即sin A>sin B;
由sin A>sin B,得2Rsin A>2Rsin B,即a>b,
所以A>B.
激趣诱思
知识点拨
微练习
不解三角形,判断下列三角形解的个数.
(1)a=5,b=4,A=120°;
(2)a=7,b=14,A=150°;
(3)a=9,b=10,A=60°.
解:(1)∵A为钝角且a>b,∴△ABC有一解.
(2)∵A为钝角且a(3)∵bsin A探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
正弦定理的简单应用
例1(1)在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
(2)在△ABC中,已知c=6,A=45°,a=2,解这个三角形.
?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 正弦定理的两个应用
(1)已知两角与任意一边解三角形的方法:
如果已知三角形的任意两个角与一边解三角形时,先由三角形内角和定理计算出三角形的第三个角,再由正弦定理计算出三角形的另两边.
(2)已知三角形两边和其中一边的对角解三角形的方法:
首先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中大边对大角看能否判断所求这个角是锐角,当已知的角为大边所对的角时,则能判断另一边所对的角为锐角,当已知的角为小边所对的角时,则不能判断,此时就有两组解,再分别求解即可;然后由三角形内角和定理求出第三个角;最后根据正弦定理求出第三条边.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 1(1)在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
(2)在△ABC中,若A=30°,BC=4,AC=4 ,则B等于( )
A.30° B.45°或135°
C.60° D.135°
(3)(2020安徽怀宁第二中学高一期中)已知a,b,c分别为△ABC内角A,B,C的对边,在△ABC中,b= a,且sin B+cos B=0,则角A的大小为 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
求三角形的面积
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 (1)三角形面积公式的选取依据
求三角形面积时通常以角为主,即在题目中已知哪个角或者涉及哪个角就以含有该角的公式进行面积的求解.
(2)在解三角形问题时需要根据正弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤:
第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向;
第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的转化;
第三步:求结果.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形的形状
例3在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin B·cos C.试判断△ABC的形状.
因为B为锐角,所以B=45°.
所以△ABC是等腰直角三角形.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 判断三角形形状的方法
(1)判断三角形的形状,可以从考查三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系或求出角与角的关系或大小,从而作出准确判断.
(2)判断三角形的形状,主要看其是不是等边三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 3在△ABC中,若b=acos C,试判断该三角形的形状.
所以sin B=sin Acos C.
因为B=π-(A+C),所以sin(A+C)=sin Acos C.
即sin Acos C+cos Asin C=sin Acos C,
所以cos Asin C=0,
所以△ABC为直角三角形.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形解的个数
例4已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,有解的作出解答.
(1)a=10,b=20,A=80°;
(2)a=2 ,b=6,A=30°.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 已知三角形两边和其中一边的对角时,判断三角形解的个数
已知三角形两边和其中一边的对角时,利用正弦定理求出另一边对角的正弦值后,需利用三角形中“大边对大角”来判断此角是锐角、直角还是钝角,从而确定三角形有两解还是只有一解.也可以用几何法来判断,即比较已知角的对边与另一边和该角正弦值乘积的大小来确定解的个数.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 4(1)(多选题)(2020江苏高一期末)已知△ABC的内角A,B,C所对的边分别为a,b,c,根据下列条件解三角形,有两解的是( )
(2)(2020黑龙江齐齐哈尔高一期中)在△ABC中,a=x,b=2,B=45°.若该三角形有两解,则x的取值范围是 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
用正弦定理证明问题
例5在任意△ABC中,求证:a(sin B-sin C)+b(sin C-sin A)+c(sin A-sin B)=0.
证明:由正弦定理,令 =2R(R为△ABC外接圆的半径),所以a=2Rsin A,b=2Rsin B,c=2Rsin C,得
左边=2R(sin Asin B-sin Asin C+sin Bsin C-sin Bsin A+sin Csin A-
sin Csin B)=0=右边,
所以等式成立.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 边与角的互化方法
正弦定理的变形公式a=2Rsin A,b=2Rsin B,c=2Rsin C(R为△ABC外接圆的半径)能够使三角形边与角的关系相互转化.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 5利用正弦定理证明定理:等腰三角形的两个底角相等.
证明:设等腰△ABC的两边AB=AC,
由于0°探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
正弦定理与三角恒等变换知识的综合应用
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形解的个数的多种方法
典例在△ABC中,角A,B,C的对边分别为a,b,c,a=4,A=30°,b=x(x>0),判断此三角形解的个数.
解:由于b是不确定的边长,无法知道a与b的大小关系,即无法判断B是锐角还是钝角,这就需要对x的取值进行分类讨论.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
所以B有两种结果,此时△ABC有两解.
当x=8时,sin B=1,则B=90°,此时△ABC有一解.
综上可知:当08时,△ABC无解.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
(方法二)A=30°,是锐角,分三种情况:
①当a=bsin A或a≥b,即4=xsin 30°或4≥x,
即x=8或0 ②当xsin 30°<4 ③当48时,△ABC无解.
综上可知,当0 当4 当x>8时,△ABC无解.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
答案:A
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
2.在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
答案:C
解析:设A=k,B=2k,C=3k,由A+B+C=180°,得6k=180°,k=30°,所以A=30°,B=60°,C=90°,a∶b∶c=sin A∶sin B∶sin C=
1∶ ∶2.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
A.直角三角形 B.等腰或直角三角形
C.不能确定 D.等腰三角形
答案:B
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
4.已知△ABC的外接圆半径是2 cm,A=60°,则BC边的长为 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
课标阐释
思维脉络
1.通过对任意三角形边长和角度的关系的探索,掌握正弦定理的内容及其证明方法.
2.能运用正弦定理与三角形的内角和定理解决简单的解三角形问题.
3.熟记并能应用正弦定理的有关变形公式解决三角形中的问题.
4.能根据条件,判断三角形解的个数.
5.能利用正弦定理、三角形面积公式解决较为复杂的三角形问题.
激趣诱思
知识点拨
在我国古代就有嫦娥奔月的神话故事.明月高悬,我们仰望星空,会有无限遐想,有人不禁会问,遥不可及的月亮离地球究竟有多远呢?其实,早在1671年,两位法国科学家就测出了地球与月球之间的距离约为385 400千米,如左侧的图所示.你知道他们是怎样测量出来的吗?提示:将左侧的图简化为右侧的图,再思考一下吧。
激趣诱思
知识点拨
知识点一:三角形的面积
常用三角形面积公式
激趣诱思
知识点拨
微练习
答案:60°或120°
激趣诱思
知识点拨
知识点二:正弦定理
1.正弦定理的表示
文字语言
在一个三角形中,各边的长和它所对角的正弦的比相等
符号语言
在△ABC中,角A,B,C所对的边分别为a,b,c,
则
激趣诱思
知识点拨
2.正弦定理的变形
=2R(R为△ABC外接圆的半径).
(1)sin A∶sin B∶sin C=a∶b∶c;
激趣诱思
知识点拨
名师点析1.使用正弦定理的前提是在同一三角形中.
2.正弦定理的主要功能是实现三角形中边角关系的转化.
3.由正弦定理可知三角形中每两边及对应角的正弦为知三求一的关系.
激趣诱思
知识点拨
微思考
(1)在直角三角形中,你能由锐角正弦值的定义探究出角与边的等式关系吗?
提示:(1)
激趣诱思
知识点拨
(2)在锐角三角形ABC中,正弦定理是否成立?
激趣诱思
知识点拨
(3)在钝角三角形ABC中,正弦定理是否成立?
提示:在钝角三角形ABC中,设C为钝角,如图,过点B作BD⊥AC交AC的延长线于点D,则BD=asin(π-C)=asin C,BD=csin A,
故有asin C=csin A,
激趣诱思
知识点拨
激趣诱思
知识点拨
(5)能否利用三角形的面积公式推出正弦定理?
激趣诱思
知识点拨
知识点三:解三角形
1.习惯上,我们把三角形的3个角与3条边都称为三角形的元素.已知三角形的若干元素求其他元素一般称为解三角形.
2.利用正弦定理可以解决以下两类有关解三角形的问题:
(1)已知两角和任意一边求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边的对角,从而进一步求出其他的边和角.
激趣诱思
知识点拨
名师点析1.应用正弦定理,要明确角化边(或边化角)的方法,对三角形有几个解必须清楚明了,防止出现漏解或增解.
2.求角问题注意大边对大角性质的应用,以便判断解的个数.
激趣诱思
知识点拨
微练习1
△ABC的内角A,B,C的对边分别为a,b,c.若
答案:D
激趣诱思
知识点拨
微练习2
答案:45°
激趣诱思
知识点拨
知识点四:对三角形解的个数的判断
已知三角形的两角和任意一边,求另两边和另一角,此时三角形被唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.现以已知a,b和A解三角形为例予以说明:
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
锐
角
①a=bsin A;
②a≥b
一解
③bsin A
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
锐
角
a
激趣诱思
知识点拨
?
图形
关系式
解的个数
A
为
钝
角
或
直
角
a>b
一解
④a≤b
无解
激趣诱思
知识点拨
微思考
在△ABC中,若A>B,一定有sin A>sin B吗?反之,若sin A>sin B,一定有A>B吗?
提示:由A>B,得a>b,
所以2Rsin A>2Rsin B,即sin A>sin B;
由sin A>sin B,得2Rsin A>2Rsin B,即a>b,
所以A>B.
激趣诱思
知识点拨
微练习
不解三角形,判断下列三角形解的个数.
(1)a=5,b=4,A=120°;
(2)a=7,b=14,A=150°;
(3)a=9,b=10,A=60°.
解:(1)∵A为钝角且a>b,∴△ABC有一解.
(2)∵A为钝角且a
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
正弦定理的简单应用
例1(1)在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
(2)在△ABC中,已知c=6,A=45°,a=2,解这个三角形.
?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 正弦定理的两个应用
(1)已知两角与任意一边解三角形的方法:
如果已知三角形的任意两个角与一边解三角形时,先由三角形内角和定理计算出三角形的第三个角,再由正弦定理计算出三角形的另两边.
(2)已知三角形两边和其中一边的对角解三角形的方法:
首先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中大边对大角看能否判断所求这个角是锐角,当已知的角为大边所对的角时,则能判断另一边所对的角为锐角,当已知的角为小边所对的角时,则不能判断,此时就有两组解,再分别求解即可;然后由三角形内角和定理求出第三个角;最后根据正弦定理求出第三条边.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 1(1)在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
(2)在△ABC中,若A=30°,BC=4,AC=4 ,则B等于( )
A.30° B.45°或135°
C.60° D.135°
(3)(2020安徽怀宁第二中学高一期中)已知a,b,c分别为△ABC内角A,B,C的对边,在△ABC中,b= a,且sin B+cos B=0,则角A的大小为 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
求三角形的面积
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 (1)三角形面积公式的选取依据
求三角形面积时通常以角为主,即在题目中已知哪个角或者涉及哪个角就以含有该角的公式进行面积的求解.
(2)在解三角形问题时需要根据正弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤:
第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向;
第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的转化;
第三步:求结果.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形的形状
例3在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin B·cos C.试判断△ABC的形状.
因为B为锐角,所以B=45°.
所以△ABC是等腰直角三角形.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 判断三角形形状的方法
(1)判断三角形的形状,可以从考查三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系或求出角与角的关系或大小,从而作出准确判断.
(2)判断三角形的形状,主要看其是不是等边三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 3在△ABC中,若b=acos C,试判断该三角形的形状.
所以sin B=sin Acos C.
因为B=π-(A+C),所以sin(A+C)=sin Acos C.
即sin Acos C+cos Asin C=sin Acos C,
所以cos Asin C=0,
所以△ABC为直角三角形.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形解的个数
例4已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,有解的作出解答.
(1)a=10,b=20,A=80°;
(2)a=2 ,b=6,A=30°.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 已知三角形两边和其中一边的对角时,判断三角形解的个数
已知三角形两边和其中一边的对角时,利用正弦定理求出另一边对角的正弦值后,需利用三角形中“大边对大角”来判断此角是锐角、直角还是钝角,从而确定三角形有两解还是只有一解.也可以用几何法来判断,即比较已知角的对边与另一边和该角正弦值乘积的大小来确定解的个数.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 4(1)(多选题)(2020江苏高一期末)已知△ABC的内角A,B,C所对的边分别为a,b,c,根据下列条件解三角形,有两解的是( )
(2)(2020黑龙江齐齐哈尔高一期中)在△ABC中,a=x,b=2,B=45°.若该三角形有两解,则x的取值范围是 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
用正弦定理证明问题
例5在任意△ABC中,求证:a(sin B-sin C)+b(sin C-sin A)+c(sin A-sin B)=0.
证明:由正弦定理,令 =2R(R为△ABC外接圆的半径),所以a=2Rsin A,b=2Rsin B,c=2Rsin C,得
左边=2R(sin Asin B-sin Asin C+sin Bsin C-sin Bsin A+sin Csin A-
sin Csin B)=0=右边,
所以等式成立.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
反思感悟 边与角的互化方法
正弦定理的变形公式a=2Rsin A,b=2Rsin B,c=2Rsin C(R为△ABC外接圆的半径)能够使三角形边与角的关系相互转化.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
变式训练 5利用正弦定理证明定理:等腰三角形的两个底角相等.
证明:设等腰△ABC的两边AB=AC,
由于0°
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
正弦定理与三角恒等变换知识的综合应用
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
判断三角形解的个数的多种方法
典例在△ABC中,角A,B,C的对边分别为a,b,c,a=4,A=30°,b=x(x>0),判断此三角形解的个数.
解:由于b是不确定的边长,无法知道a与b的大小关系,即无法判断B是锐角还是钝角,这就需要对x的取值进行分类讨论.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
所以B有两种结果,此时△ABC有两解.
当x=8时,sin B=1,则B=90°,此时△ABC有一解.
综上可知:当0
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
(方法二)A=30°,是锐角,分三种情况:
①当a=bsin A或a≥b,即4=xsin 30°或4≥x,
即x=8或0
综上可知,当0
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
答案:A
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
2.在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
答案:C
解析:设A=k,B=2k,C=3k,由A+B+C=180°,得6k=180°,k=30°,所以A=30°,B=60°,C=90°,a∶b∶c=sin A∶sin B∶sin C=
1∶ ∶2.
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
A.直角三角形 B.等腰或直角三角形
C.不能确定 D.等腰三角形
答案:B
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
4.已知△ABC的外接圆半径是2 cm,A=60°,则BC边的长为 .?
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
素养形成
当堂检测
