4.2 直线、射线、线段(第二课时)课件
文档属性
| 名称 | 4.2 直线、射线、线段(第二课时)课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 289.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-02 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
4.2 直线、射线、线段(2)
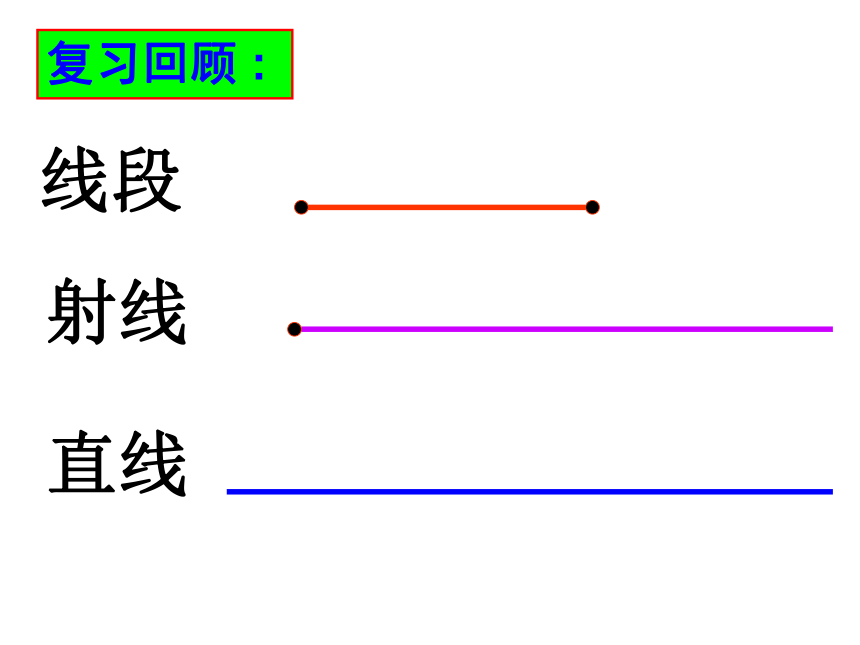
线段
射线
直线
复习回顾 :
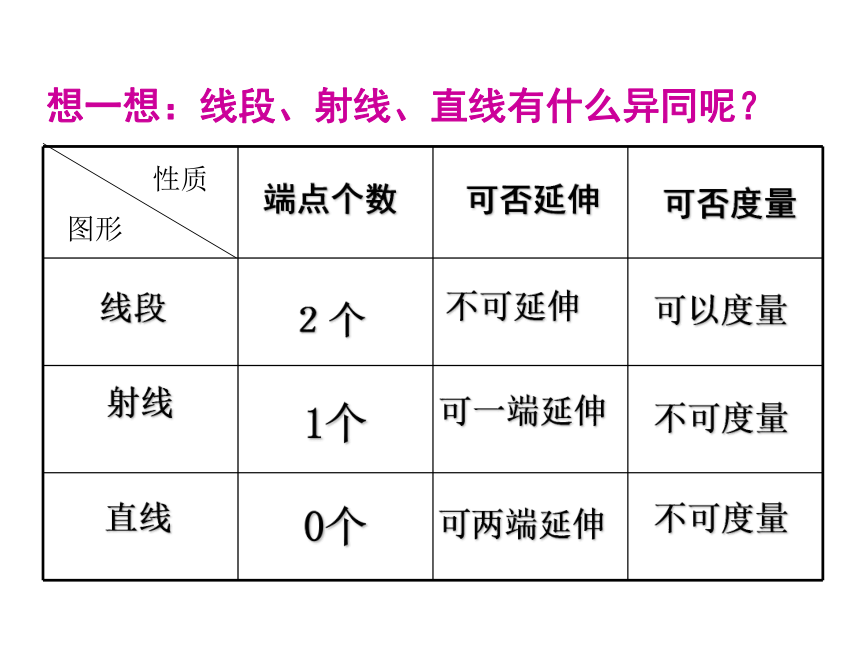
想一想:线段、射线、直线有什么异同呢?
线段
射线
直线
端点个数
可否延伸
可否度量
可两端延伸
可一端延伸
不可延伸
可以度量
不可度量
不可度量
图形
性质
2个
1个
0个
思考 :怎样比较两个同学的高矮?
比较两个同学高矮的方法:
②让两个同学站在同一平地上,脚底平齐,背靠背,观看两人的头顶,直接比出高矮
——叠合法.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
议一议 :
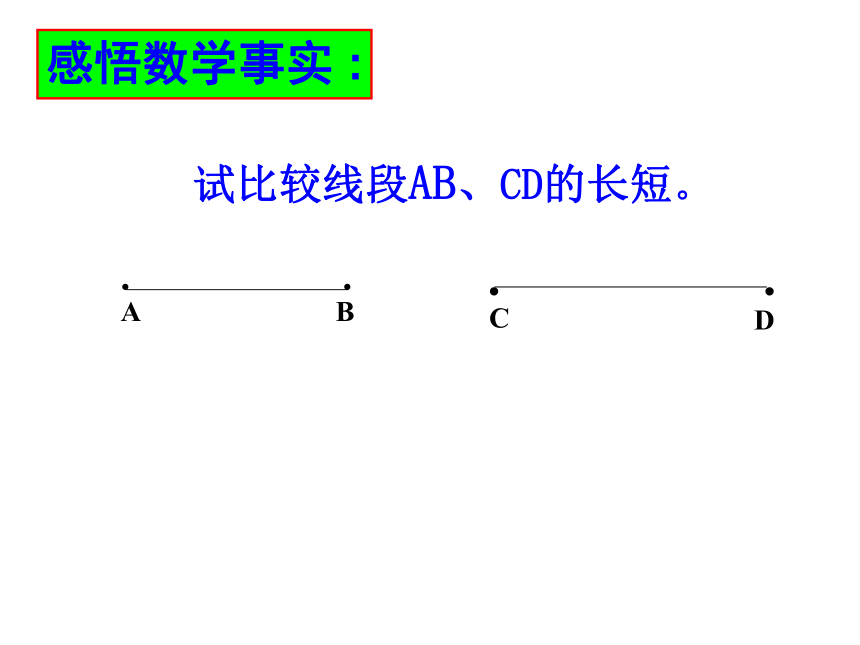
试比较线段AB、CD的长短。
.
.
A
B
C
D
感悟数学事实 :
A
B
D
C
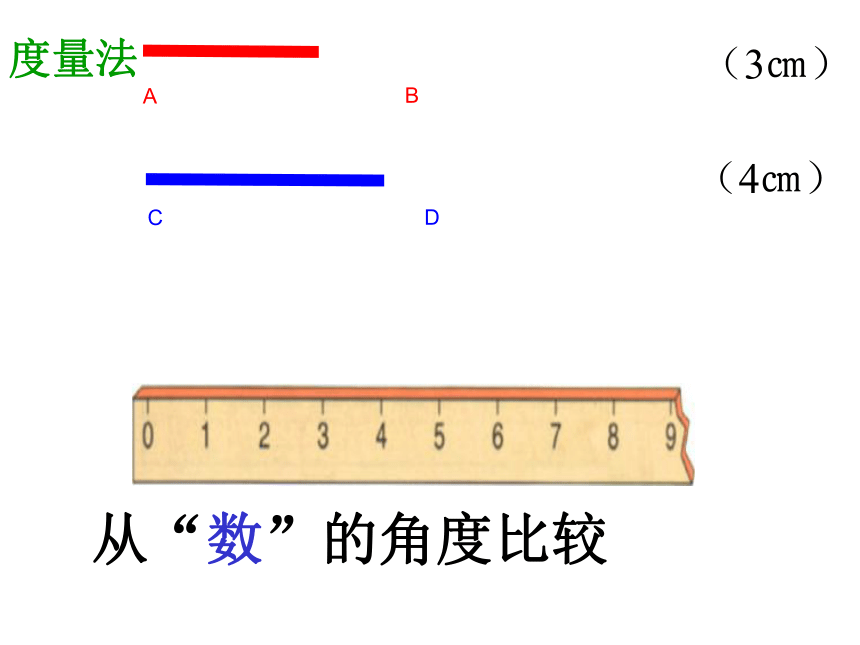
(4㎝)
(3㎝)
度量法
从“数”的角度比较
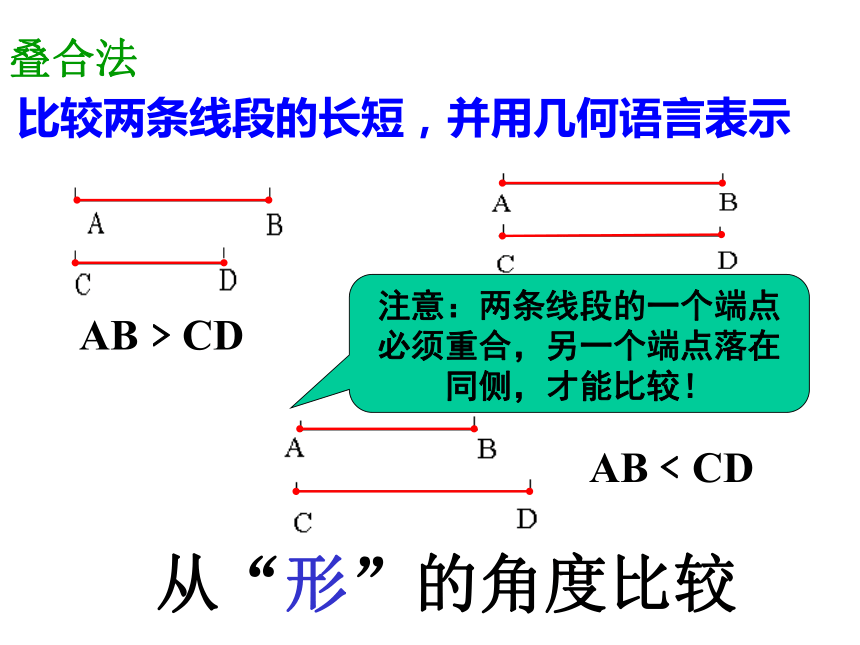
比较两条线段的长短,并用几何语言表示
AB﹥CD
AB=CD
AB﹤CD
从“形”的角度比较
叠合法
注意:两条线段的一个端点必须重合,另一个端点落在同侧,才能比较!
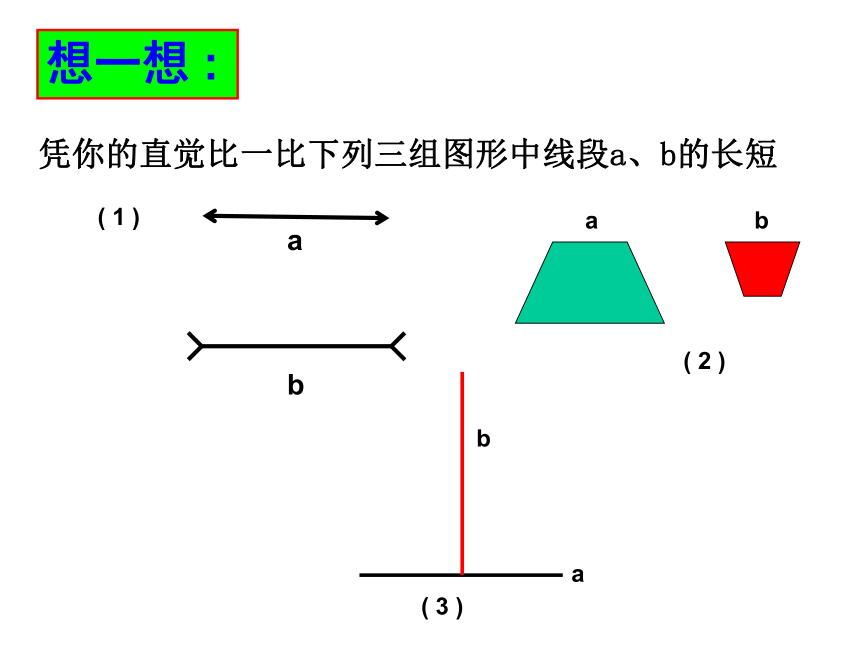
凭你的直觉比一比下列三组图形中线段a、b的长短
a
b
( 1 )
( 2 )
a
b
a
b
( 3 )
想一想 :
如果两条线段不能移动,又无法准确度量线段的长,你能用圆规比较出两条线段的长短吗
完成:书131页练习1
思考探究 :
A
B
如何作一条线段等于已知线段
用直尺和圆规作一条线段等于已知线段MN。
① 先用直尺画一条射线AB;
② 用圆规量出已知线段MN的长度;
③ 在射线AB上以A为圆心, 截取AC = MN .
C
则AC为
所作的线段
M
N
探究3 :
利用直尺和圆规作一条线段
使它等于两条已知线段的和a+b.
合作探究 :
画线段的和、差
1.利用直尺和圆规作一条线段
使它等于两条已知线段的差a-b.
2.利用直尺和圆规完成书131页练习第2题.
观察下列步骤,并回答问题
(1)拿出一张白纸
(2)对折这张白纸
(3)把白纸展开铺平,发现在边AB上有个折痕点M,请问AM和BM相等吗?
A
B
M
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点,可知AM=BM=
几何语言
探究4 :
点M在线段AB上
因为 AM=BM
所以 点M是线段AB的中点
大前提
1、如图,点C在线段AB上,且点C是线段AB的中点
(1)若AB=6cm,则AC= cm。
(2)若AC=6cm,则AB= cm。
3
12
反馈练习 :
3.给你一根绳,不量取,你能找到它的中点吗?
(1)若P是线段AB的中点,则AP=BP.
(2)若AP=BP,则P是线段AB的中点.
2.判断正误:
对折即可。
反馈练习 :
已知,如图AC=CD=DE=EF=FB
①点C是 的中点,是 的一个三等分点,又是 的一个四等分点,也是 的一个五等分点
② CF= + + 。
AC=AE- 。
③ AD= AC,AE= AC,
AC= AF,AC= AB,
④ AD= AE,AE= AB,
A
B
C
D
E
F
反馈练习 :
AD
AE
AF
AB
CD
DE
EF
CE
2
3
1/4
1/5
2/3
3/5
如图:从A地到B地有四条道路,除它们外能否再找一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
怎样走最近
结论:两点的所有连线中,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
A
B
结论:两点的所有连线中,线段最短.
探究5 :
简单说成:
2.下列说法正确的是( )
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度,叫做两点间的距离
C、连结两点的直线的长度,叫做两点的距离
D、连结两点的线段的长度,叫做两点间的距离
A
C
B
1.如右图,比较:AC+CB AB
反馈练习 :
根据: 。
今天,你都收获了什么?
作业:
必做:教材P133页7、8;P134页 9
选做:P134页 10
如图,C是AB上的点,BC=6cm,AC=10cm,D是AC的中点,E是BC的中点,求线段DE的长。
.
.
.
.
.
A
B
C
D
E
变式: 如图,C是AB上的点,AB=16cm,D是AC的中点,E是BC的中点,求线段DE的长。
.
.
.
.
.
A
B
C
D
E
能力提升 :
有条小河L,点A,B表示在河两岸的两个村庄,现在要建造一座小桥,请你找出造桥的位置,使得A,B两村的路程最短,并说明理由。
L
A
B
桥
趣味思考 :
4.2 直线、射线、线段(2)
线段
射线
直线
复习回顾 :
想一想:线段、射线、直线有什么异同呢?
线段
射线
直线
端点个数
可否延伸
可否度量
可两端延伸
可一端延伸
不可延伸
可以度量
不可度量
不可度量
图形
性质
2个
1个
0个
思考 :怎样比较两个同学的高矮?
比较两个同学高矮的方法:
②让两个同学站在同一平地上,脚底平齐,背靠背,观看两人的头顶,直接比出高矮
——叠合法.
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
议一议 :
试比较线段AB、CD的长短。
.
.
A
B
C
D
感悟数学事实 :
A
B
D
C
(4㎝)
(3㎝)
度量法
从“数”的角度比较
比较两条线段的长短,并用几何语言表示
AB﹥CD
AB=CD
AB﹤CD
从“形”的角度比较
叠合法
注意:两条线段的一个端点必须重合,另一个端点落在同侧,才能比较!
凭你的直觉比一比下列三组图形中线段a、b的长短
a
b
( 1 )
( 2 )
a
b
a
b
( 3 )
想一想 :
如果两条线段不能移动,又无法准确度量线段的长,你能用圆规比较出两条线段的长短吗
完成:书131页练习1
思考探究 :
A
B
如何作一条线段等于已知线段
用直尺和圆规作一条线段等于已知线段MN。
① 先用直尺画一条射线AB;
② 用圆规量出已知线段MN的长度;
③ 在射线AB上以A为圆心, 截取AC = MN .
C
则AC为
所作的线段
M
N
探究3 :
利用直尺和圆规作一条线段
使它等于两条已知线段的和a+b.
合作探究 :
画线段的和、差
1.利用直尺和圆规作一条线段
使它等于两条已知线段的差a-b.
2.利用直尺和圆规完成书131页练习第2题.
观察下列步骤,并回答问题
(1)拿出一张白纸
(2)对折这张白纸
(3)把白纸展开铺平,发现在边AB上有个折痕点M,请问AM和BM相等吗?
A
B
M
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点,可知AM=BM=
几何语言
探究4 :
点M在线段AB上
因为 AM=BM
所以 点M是线段AB的中点
大前提
1、如图,点C在线段AB上,且点C是线段AB的中点
(1)若AB=6cm,则AC= cm。
(2)若AC=6cm,则AB= cm。
3
12
反馈练习 :
3.给你一根绳,不量取,你能找到它的中点吗?
(1)若P是线段AB的中点,则AP=BP.
(2)若AP=BP,则P是线段AB的中点.
2.判断正误:
对折即可。
反馈练习 :
已知,如图AC=CD=DE=EF=FB
①点C是 的中点,是 的一个三等分点,又是 的一个四等分点,也是 的一个五等分点
② CF= + + 。
AC=AE- 。
③ AD= AC,AE= AC,
AC= AF,AC= AB,
④ AD= AE,AE= AB,
A
B
C
D
E
F
反馈练习 :
AD
AE
AF
AB
CD
DE
EF
CE
2
3
1/4
1/5
2/3
3/5
如图:从A地到B地有四条道路,除它们外能否再找一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
怎样走最近
结论:两点的所有连线中,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
A
B
结论:两点的所有连线中,线段最短.
探究5 :
简单说成:
2.下列说法正确的是( )
A、连结两点的线段叫做两点间的距离
B、两点间的连线的长度,叫做两点间的距离
C、连结两点的直线的长度,叫做两点的距离
D、连结两点的线段的长度,叫做两点间的距离
A
C
B
1.如右图,比较:AC+CB AB
反馈练习 :
根据: 。
今天,你都收获了什么?
作业:
必做:教材P133页7、8;P134页 9
选做:P134页 10
如图,C是AB上的点,BC=6cm,AC=10cm,D是AC的中点,E是BC的中点,求线段DE的长。
.
.
.
.
.
A
B
C
D
E
变式: 如图,C是AB上的点,AB=16cm,D是AC的中点,E是BC的中点,求线段DE的长。
.
.
.
.
.
A
B
C
D
E
能力提升 :
有条小河L,点A,B表示在河两岸的两个村庄,现在要建造一座小桥,请你找出造桥的位置,使得A,B两村的路程最短,并说明理由。
L
A
B
桥
趣味思考 :
