2.6 弧长与扇形面积( 第2课时) 扇形面积 课件(共19张PPT)
文档属性
| 名称 | 2.6 弧长与扇形面积( 第2课时) 扇形面积 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 10:25:39 | ||
图片预览



文档简介
(共19张PPT)
扇形面积
第2章
圆
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握扇形的定义.
2.掌握扇形面积公式的推导过程,会运用扇形的面积进行有关计算.
【过程与方法】
经过扇形面积公式的推导,培养学生抽象、理解、概括、归纳能力和迁移能力.
【情感态度】
经历扇形面积公式的推导过程及利用公式解决实际问题,加强合作交流,集思广益.
【教学重点】
扇形面积公式的推导过程及用公式进行有关计算.
【教学难点】
用公式求组合图形的面积来解决实际问题.
如图所示是一把圆弧形状的扇子的示意图,你能求出做这把扇子用了多少纸吗?
新课探究
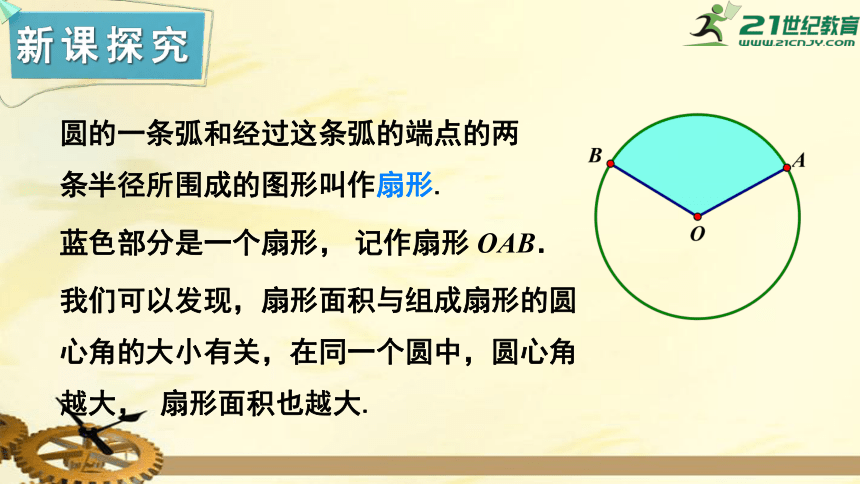
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
蓝色部分是一个扇形,
记作扇形
OAB.
我们可以发现,扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大,
扇形面积也越大.
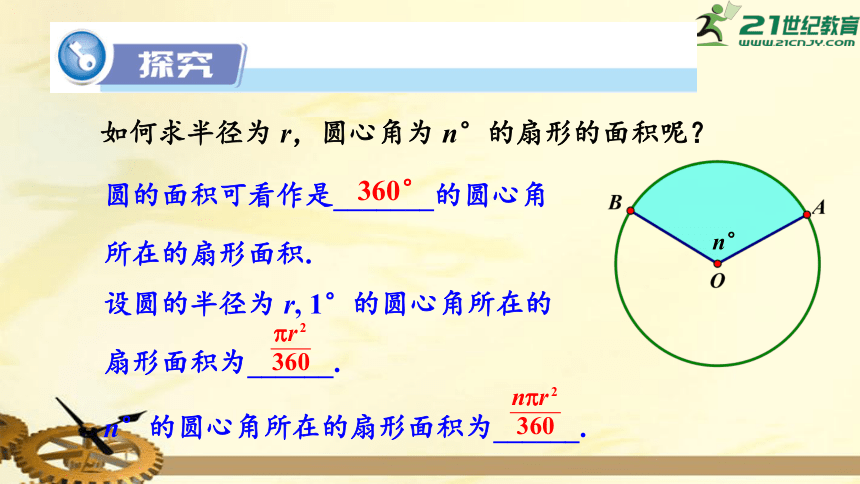
如何求半径为
r,圆心角为
n°的扇形的面积呢?
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为
r,
1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
n°
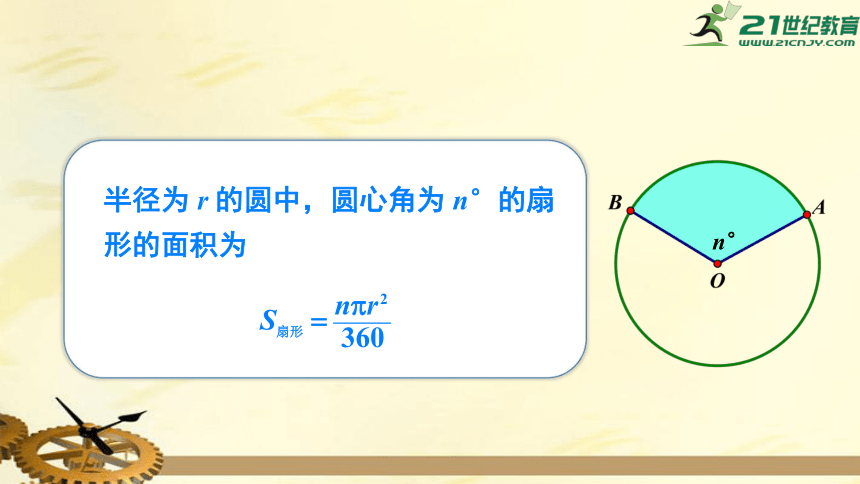
半径为
r
的圆中,圆心角为
n°的扇形的面积为
n°
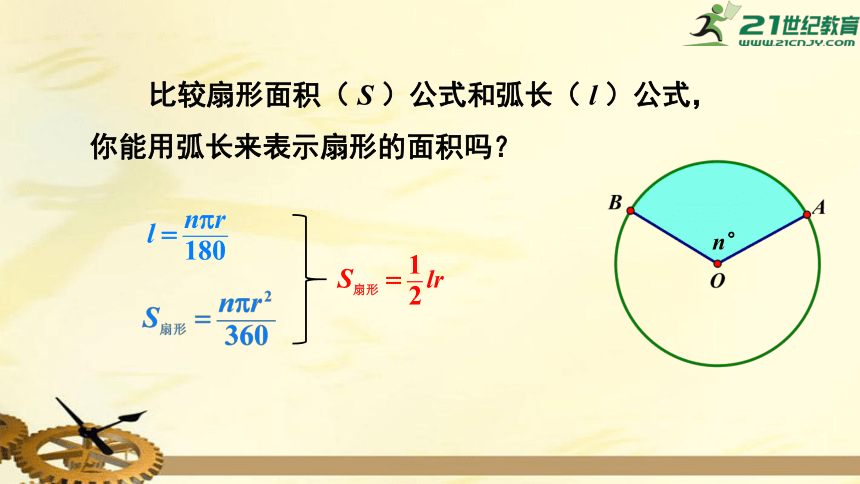
比较扇形面积(
S
)公式和弧长(
l
)公式,你能用弧长来表示扇形的面积吗?
n°
如图,⊙O
的半径为
1.5
cm,圆心角∠AOB
=
58°,求扇形
OAB
的面积(精确到
0.1
cm2).
解
∵
r
=
1.5
cm
,n
=
58
,
如图,是一条圆弧形弯道,已知
OA
=20
m,OC
=
12
m,
的长度为
9π
m,求圆弧形弯道的面积.
解设∠AOB
=
n°,
∵
OC
=
12
m,
的长度为
9π
m,
∴
解得
n
=
135,即圆心角∠COD
=
135
°
.
∴
∴S扇形ACDB
=
S扇形OAB
-
S扇形OCD
=
150π
-
54π
=
96π(m2)
答:这条圆弧形弯道的面积为
96π
m2.
练习
如图,在⊙O
中,∠AOB
=
120°,弦
AB
的长为
cm,
求扇形
OAB
的面积.
解:作
OD
⊥
AB
,
由题可求出OA
=
2(cm)
答:扇形
OAB
的面积为
4.2
cm2.
2.
如图,分别以△ABC
的顶点
A,B,C
为圆心,
以
1
为半径画圆,求图中绿色部分的面积.
解:∠A+
∠B+
∠C
=
180°
绿色部分可以看成半径为
1,圆心角为180°的扇形.
3.
如图,有一直径是
20
cm
的圆形纸片,现从中剪出一个圆心角是
90°的扇形
ABC,求被剪掉部分的面积.
解:连接BC,则
BC
=
20
cm
又因为
AB
=
AC,
所以△ABC为等腰直角三角形.
随堂练习
1.
如图,
AB
是☉O
的直径,
弦
CD
⊥
AB,∠CDB
=
30°,
CD
=
,
则阴影部分的面积为(
)
A.
2π
B.
π
C.
D.
D
2.
(山西中考)如图是某商品的标志图案,
AC
与
BD
是☉O
的两条直径,首尾顺次连接点
A
,
B
,
C
,
D
,得到四边形
ABCD
.若
AC
=
10
cm,
∠BAC
=36°,
则
图中阴影部分的面积为(
)
A.
5π
cm2
B.
10π
cm2
C.
15π
cm2
D.
20π
cm2
B
3.如图为一座圆弧形拱桥的示意图,拱形的半径为20
m,
拱的跨度
AB
为
m
.
求:(1)拱形的弧长;
(2)扇形
OAB
的面积.
解:∠AOB
=
120°
1.扇形的概念;
课堂小结
2.圆心角为
n°的扇形的面积为
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
扇形面积
第2章
圆
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握扇形的定义.
2.掌握扇形面积公式的推导过程,会运用扇形的面积进行有关计算.
【过程与方法】
经过扇形面积公式的推导,培养学生抽象、理解、概括、归纳能力和迁移能力.
【情感态度】
经历扇形面积公式的推导过程及利用公式解决实际问题,加强合作交流,集思广益.
【教学重点】
扇形面积公式的推导过程及用公式进行有关计算.
【教学难点】
用公式求组合图形的面积来解决实际问题.
如图所示是一把圆弧形状的扇子的示意图,你能求出做这把扇子用了多少纸吗?
新课探究
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.
蓝色部分是一个扇形,
记作扇形
OAB.
我们可以发现,扇形面积与组成扇形的圆心角的大小有关,在同一个圆中,圆心角越大,
扇形面积也越大.
如何求半径为
r,圆心角为
n°的扇形的面积呢?
圆的面积可看作是_______的圆心角所在的扇形面积.
设圆的半径为
r,
1°的圆心角所在的扇形面积为______.
n°的圆心角所在的扇形面积为______.
360°
n°
半径为
r
的圆中,圆心角为
n°的扇形的面积为
n°
比较扇形面积(
S
)公式和弧长(
l
)公式,你能用弧长来表示扇形的面积吗?
n°
如图,⊙O
的半径为
1.5
cm,圆心角∠AOB
=
58°,求扇形
OAB
的面积(精确到
0.1
cm2).
解
∵
r
=
1.5
cm
,n
=
58
,
如图,是一条圆弧形弯道,已知
OA
=20
m,OC
=
12
m,
的长度为
9π
m,求圆弧形弯道的面积.
解设∠AOB
=
n°,
∵
OC
=
12
m,
的长度为
9π
m,
∴
解得
n
=
135,即圆心角∠COD
=
135
°
.
∴
∴S扇形ACDB
=
S扇形OAB
-
S扇形OCD
=
150π
-
54π
=
96π(m2)
答:这条圆弧形弯道的面积为
96π
m2.
练习
如图,在⊙O
中,∠AOB
=
120°,弦
AB
的长为
cm,
求扇形
OAB
的面积.
解:作
OD
⊥
AB
,
由题可求出OA
=
2(cm)
答:扇形
OAB
的面积为
4.2
cm2.
2.
如图,分别以△ABC
的顶点
A,B,C
为圆心,
以
1
为半径画圆,求图中绿色部分的面积.
解:∠A+
∠B+
∠C
=
180°
绿色部分可以看成半径为
1,圆心角为180°的扇形.
3.
如图,有一直径是
20
cm
的圆形纸片,现从中剪出一个圆心角是
90°的扇形
ABC,求被剪掉部分的面积.
解:连接BC,则
BC
=
20
cm
又因为
AB
=
AC,
所以△ABC为等腰直角三角形.
随堂练习
1.
如图,
AB
是☉O
的直径,
弦
CD
⊥
AB,∠CDB
=
30°,
CD
=
,
则阴影部分的面积为(
)
A.
2π
B.
π
C.
D.
D
2.
(山西中考)如图是某商品的标志图案,
AC
与
BD
是☉O
的两条直径,首尾顺次连接点
A
,
B
,
C
,
D
,得到四边形
ABCD
.若
AC
=
10
cm,
∠BAC
=36°,
则
图中阴影部分的面积为(
)
A.
5π
cm2
B.
10π
cm2
C.
15π
cm2
D.
20π
cm2
B
3.如图为一座圆弧形拱桥的示意图,拱形的半径为20
m,
拱的跨度
AB
为
m
.
求:(1)拱形的弧长;
(2)扇形
OAB
的面积.
解:∠AOB
=
120°
1.扇形的概念;
课堂小结
2.圆心角为
n°的扇形的面积为
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
