26.1 反比例函数课件(共3课时 68张)
文档属性
| 名称 | 26.1 反比例函数课件(共3课时 68张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 10:04:50 | ||
图片预览











文档简介
(共68张PPT)
第二十六章 反比例函数
26.1 反比例函数
26.1.1 反比例函数
一、情景导入
问题
1 京沪线铁路全程为
1
463
km,某次列车的平均速度
v(单位:km/h)随此次列车的全程运行时间
t(单位:h)的变化而变化;
思考:(1)平均速度
v
和时间
t
存在着怎样的关系?
(2)这三者中,谁是常量,谁是变量?
(3)两个变量间具有函数关系吗?
(4)能写出列车的平均速度
v
随此次列车的全程运行时间
t
的函数关系吗?
一、情景导入
问题
2 下列问题中,变量间具有函数关系吗?如果有,请直接写出解析式.
(1)某住宅小区要种植一块面积为
1
000
m2
的矩形草坪,草坪的长
y(单位:m)随宽
x(单位:m)的变化而变化;
一、情景导入
(2)已知北京市的总面积为
1.68×104
km2
,人均占有面积
S(单位:km2
/人)随全市总人口
n(单位:人)的变化而变化.
二、探究新知
,
,
.
思考 这些解析式有什么共同特征?
归纳 上述解析式具有
的形式,其中
k
是非零常数.
二、探究新知
定义:一般地,形如
(k为常数,k≠0)的函数,叫做反比例函数,其中
x
是自变量,y
是函数.
思考:自变量
x
及函数值
y
的取值范围?
x≠0
,y≠0
.
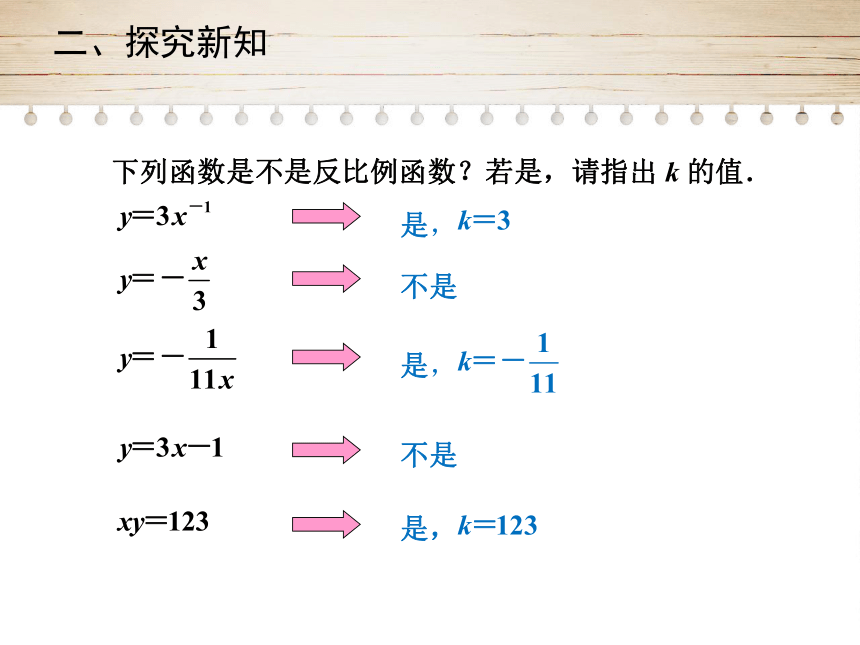
下列函数是不是反比例函数?若是,请指出
k
的值.
二、探究新知
是,
不是
不是
是,
是,
思考:反比例函数的表达形式有哪些?
二、探究新知
二、探究新知
例
1 已知
y
是
x
的反比例函数,并且当
x=2
时,y=6.
(1)写出
y
关于
x
的函数解析式;
(2)当
x=4
时,求
y
的值.
思考:求函数解析式常用方法是什么?
待定系数法.
先设出函数解析式,再根据条件确定解析式中未知数的系数,从而得出函数解析式.
二、探究新知
解:(1)设
因为当
x=2
时,y=6,所以有
解得
k=12.
因此
(2)把
x=4
代入
,得
二、探究新知
方法总结:用待定系数法求反比例函数解析式的一般步骤:①
设出含有待定系数的反比例函数解析式
;
②
将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;③
解方程,求出待定系数;④
写出反比例函数解析式.
二、探究新知
已知
y
与
x+1
成反比例,并且当
x=3
时,y=4.
(1)写出
y
关于
x
的函数解析式;
(2)当
x=7
时,求
y
的值.
解:(1)设
.因为当
x=3
时,y=4,所以有
解得
k=1.
(2)把
x=7
代入
,得
三、课堂小结
用待定系数法求反比例函数解析式
反比例函数
反比例函数
定义
三种表达方式
四、课堂训练
1.下列函数中,y
是
x
的反比例函数的是( ).
A.
B.
C.
D.
A
四、课堂训练
2.生活中有许多反比例函数的例子,在下面的实例中,x
和
y
成反比例函数关系的有( ).
①
x
人共饮水
10
kg,平均每人饮水
y
kg;②
底面半径为
x
m,高为
y
m的圆柱形水桶的体积为
10
m3;③
用铁丝做一个圆,铁丝的长为
x
cm,做成圆的半径为
y
cm;④
在水龙头前放满一桶水,出水的速度为
x,放满一桶水的时间
y.
A.1
个
B.2
个
C.3
个
D.4
个
B
3.填空:
(1)若
是反比例函数,则
m
的取值范围是_____.
(2)若
是反比例函数,则
m
的取值范围是________________
.
(3)若
是反比例函数,则
m
的取值范围是
__________.
m≠0
且
m≠-2
四、课堂训练
m≠1
m=-1
四、课堂训练
4.已知变量
y
与
x
成反比例,且当
x=3
时,y=-4.
(1)写出
y
关于
x
的函数解析式;
(2)当
y=6
时,求
x
的值.
解:(1)设
因为当
x=3
时,y=-4,所以有
解得
k=-12.
因此,y
关于
x
的函数解析式为
四、课堂训练
(2)把
y=6
代入
,得
解得
x=-2.
四、课堂训练
5.小明家离学校
1
000
m,每天他往返于两地之间,有时步行,有时骑车.假设小明每天上学时的平均速度为
v(m/min),所用的时间为
t(min).
(1)求变量
v
和
t
之间的函数关系式;
解:
(t>0).
四、课堂训练
(2)小明星期二步行上学用了
25
min,星期三骑自行车上学用了
8
min,那么他星期三上学时的平均速度比星期二快多少?
解:当
t=25
时,
当
t=8
时,
125-40=85(m/min).
答:他星期三上学时的平均速度比星期二快
85
m/min.
五、作业
必做题:习题
26.1
第
1,2,4
题.
选做题:已知函数
y=y1+y2,且
y1
与
x
成正比例,y2
与
x
成反比例,且当
x=1
时,y=5;当
x=2
时,y=4.
(1)求
y
与
x
的函数关系式.
(2)当
x=-2
时,求函数
y
的值.
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第一课时
一、情景导入
1.什么是反比例函数?
一般地,形如
(k
是常数,k≠0
)的函数叫做反比例函数.
2.反比例函数的定义中需要注意什么?
(1)k
是非零常数.
(2)x≠0,y≠0.
(3)xy=k,y=kx-1
.
3.还记得一次函数的图象与性质吗?
4.还记得二次函数的图象与性质吗?
5.如何画函数的图象?
反比例函数的图象与性质又如何呢?
这节课开始我们来一起探究吧.
一、情景导入
画函数图象的方法
描点法
列
表
描
点
连
线
二、探究新知
我们先研究
k>0
的情形.
例
2 画出反比例函数
和
的函数图象.
温馨提示
列表,描点,连线的注意事项是什么?
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
…
-2
-2.4
-3
-4
-6
-12
12
6
4
3
2.4
2
…
二、探究新知
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
二、探究新知
思考:观察这两个函数图象,回答问题:
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着
x
的增大,y
如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数
(k>0),考虑问题(1)(2),你能得出同样的结论吗?
二、探究新知
归纳:对于反比例函数
,当
k>0
时,
(1)函数图象分别位于第一,三象限内;
(2)在每一个象限内,y
随
x
的增大而减小.
二、探究新知
回顾前面我们利用函数图象,从特殊到一般研究反比例函数
(k>0)的性质的过程,你能用类似的方法研究反比例函数
(k<0)的图象和性质吗?
二、探究新知
画出反比例函数
和
的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
二、探究新知
你能说出反比例函数
(k<0)的性质吗?
归纳
对于反比例函数
当
k<0
时,
(1)函数图象分别位于第二,四象限内;
(2)在每一个象限内,y
随
x
的增大而增大.
反比例函数的图象有两条曲线组成,它是双曲线.
二、探究新知
一般地,反比例函数
的图象是双曲线,它具有以下性质:
(1)当
k
>0
时,
双曲线的两支分别位于第一,第三象限,在每一个象限内,y
随
x
的增大而减小.
(2)当
k
<0
时,
双曲线的两支分别位于第二,第四象限,在每一个象限内,y
随
x
的增大而增大.
二、探究新知
在同一坐标系中反比例函数
与
的图象在位置上有什么关系?
二、探究新知
结论:
当
k
互为相反数时,对应的反比例函数图象既关于
x
轴对称,也关于
y
轴对称.
二、探究新知
1.下列图象中,可以是反比例函数的图象的( ).
A.
B.
C.
D.
D
二、探究新知
2.反比例函数
的图象大致( ).
A.
B.
C.
D.
x
y
o
x
o
y
x
y
o
x
y
o
C
二、探究新知
3.
函数
的图象在第________象限,在每一象限内,y
随
x
的增大而_________.
4.函数
的图象在第________象限,在每一象限内,y
随
x
的增大而_________.
5.函数
当
x>0
时,图象在第____象限,y
随
x
的增大而_________.
一,三
二,四
一
减小
增大
减小
二、探究新知
6.已知点
A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,试比较
a,b,c
的大小.
解:把点
A(-2,a),B(-1,b),C(3,c)分别带入函数
中得:
所以
b<a<c.
二、探究新知
另解:因为
k=1>0,所以在每个象限内
y
随
x
的增大而减小,由图知,因为
-2<-1<0,所以
b<a<0,而
c>0,所以
b<a<c.
三、课堂小结
本节课我们学习了哪些知识?
k>0时,在每个象限内,y
随
x
的增大而减小
函数的
增减性
k<0时,在二、四象限
k>0时,在一、三象限
图象为双曲线
k<0时,在每个象限内,y
随
x
的增大而增大
分类讨论
四、课堂训练
6.对于反比例函数
下列说法正确的是( ).
A.其图象经过(2,-1)
B.其图象位于第二,四象限
C.当
x<0
时,y
随
x
值的增大而减小
D.当
x>0
时,y
随
x
值的增大而增大
7.下列反比例函数图象一定在第一,三象限的是( ).
A.
B.
C.
D.
C
C
四、课堂训练
8.甲乙两地相距
100
km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间
y(h)表示为汽车的平均速度
x(km/h)
的函数,则这个函数的图象大致是( ).
A.
B.
C.
D.
C
四、课堂训练
9.函数
y=kx-3
与
(k≠0)在同一坐标系内的图象可能是( ).
A.
B.
C.
D.
B
五、作业
必做题:教科书习题
26.1
第
3,8
题.
选做题:
1.函数
y=kx-k
与
(k≠0)的图象大致是( ).
x
y
O
y
y
x
x
y
O
O
O
x
D
A.
B.
C.
D.
五、作业
2.在同一直角坐标系中,函数
与
y=ax+1(a≠0)的图象可能是( ).
y
x
O
y
x
O
y
x
O
y
x
O
B
A.
B.
C.
D.
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第二课时
一、情景导入
1.什么是反比例函数?
一般地,形如
(k是常数,
k≠0
)的函数叫做反比例函数.
2.反比例函数的图象和性质是什么?
一般地,反比例函数
的图象是双曲线.
(1)当
k>0
时,
双曲线的两支分别位于第一,第三象限,在每一个象限内,y
随
x
的增大而减小.
(2)当
k<0
时,
双曲线的两支分别位于第二,第四象限,在每一个象限内,y
随
x
的增大而增大.
一、情景导入
例
3 已知反比例函数的图象经过点
A(2,6).
(1)这个函数的图象位于哪些象限?y
随
x
的增大如何变化?
(2)
点
B(3,4),C(
),D(2,5)是否在这个函数的图象上?
解:(1)因为点
A
(2,6)
在第一象限,所以这个函数的图象位于第一,三象限,在每一个象限内,y
随
x
的增大而减小.
一、情景导入
(2)设这个反比例函数的解析式为
,因为点
A(2,6)在其图象上,所以点
A
的坐标满足
,即
解得
k=12.
所以这个反比例函数的解析式为
因为点
B,C
的坐标都满足
,点
D
的坐标不满足
,所以点
B,C
在函数
的图象上,点
D
不在这个函数的图象上.
二、探究新知
已知反比例函数
的图象经过点
A(2,3).
(1)求这个函数的表达式;
(2)判断点
B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当
-3<x<-1
时,求
y
的取值范围.
二、探究新知
解:(1)因为反比例函数
的图象经过点
A(2
,3),所以点
A
的坐标满足
即
.
解得
k=6.
所以这个函数的表达式为
(2)分别把点
B,C
的坐标代入
,点
B
的坐标不满足
点
C
的坐标满足
,所以点
B
不在
的图象上,点
C
在这个函数的图象上.
二、探究新知
(3)因为 当
x=-3
时,y=-2;当
x=-1
时,y=-6,且
k>0,
所以 当
x<0
时,y
随
x
的增大而减小.
所以 当
-3<x<-1
时,-6<y<-2.
二、探究新知
例
4 如图,它是反比例函数
图象的一支.根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数
m
的取值范围是什么?
(2)在这个函数图象的某一支上任取点
A(x1,y1)和点
B
(x2,y2).如果
x1>x2,那么
y1
和
y2
有怎样的大小关系?
二、探究新知
解:(1)反比例函数的图象只有两种可能:位于第一,第三象限,或者位于第二,第四象限.因为这个函数的图象的一支位于第一象限,所以另一支必位于第三象限.因为这个函数的图象位于第一,第三象限,所以
m-5>0.
解得
m>5.
(2)因为
m-5>0,所以在这个函数图象
的任一支上,y
都随
x
的增大而减小,因此当
x1>x2
时,
y1<y2
.
O
x
y
二、知识拓展
已知反比例函数
的图象上有两点:A(x1,y1),B
(x2,y2)上,且
x1<x2<0
,那么下列结论正确的是( ).
A.
y1<y2
B.
y1>
y2
C.
y1=y2
D.
y1与y2大小不能确定
A
二、探究新知
如图,在反比例函数
的图象上分别取点
P,Q
向
x
轴,y
轴作垂线,围成面积分别为S1,S2
的矩形.
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
二、探究新知
P(2,2)
Q(4,1)
S1
的值
4
S2
的值
4
S1
与
S2
的关系
S1=S2
猜想
S1,S2
与
k
的关系
S1=S2=k
二、探究新知
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
二、探究新知
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
S1=S2=4=|-4|=k
二、探究新知
归
纳 若点
P
是
图象上的任意一点,作
PA
垂直于
x
轴,作
PB
垂直于
y
轴,矩形
AOBP
的面积与
k
的关系是
S矩形
AOBP=|k|.
二、探究新知
1.如图,反比例函数
的图象上的点
M(1,a),过
M
分别作
y
轴和
x
轴的垂线,垂足是
P,Q;则
a=_____;矩形
OQMP
的面积=__________;△PMO
的面积=_____;△QMO
的面积=_____.
2.若点
P
是反比例函数图象上的一
点,过点
P
分别向
x
轴,y
轴作垂线,垂
足分别为点
M,N,若四边形
PMON
的
面积为
3,则这个反比例函数的关系式是
________________.
2
2
1
1
三、课堂小结
1.反比例函数的图象与性质;
2.反比例函数的图象与性质的简单应用.
四、课堂训练
1.若反比例函数的图象经过点(-3,-4),则函数的图象应该在( ).
A.第一,三象限
B.第一,二象限
C.第二,四象限
D.第三,四象限
2.若点(-2,y1),(-1,y2),(2,y3)在反比例函数
的图象上,则( ).
A.
y1>y2>y3
B.y2>y1>y3
C.
y3>y1>y2
D.y3>y2>y1
A
B
四、课堂训练
3.若点(-2,y1),(-1,y2),(2,y3)在反比例函数
的图象上,则(
).
A.y1>y2>y3
B.y2>y1>y3
C.y>y1>y2
D.y3>y2>y1
4.已知反比例函数
(k
是不为
0
的常数)的图象在第二,四象限,那么一次函数
y=kx-k
的图象经过( ).
A.第一,二,三象限
B.第一,二,四象限
C.第一,三,四象限
D.第二,三,四象限
D
C
四、课堂训练
5.考察函数
的图象,当
x=-2
时,y=_______,
当
x<-2
时,
y
的取值范围是__________;当
y>-1
时,x
的取值范围是________________.
-1
-1<y<0
x<-2
或
x>0
四、课堂训练
6.如图是一次函数
y1=kx+b
和反比例函数
的图象,观察图象写出
y1>y2
时,x
的取值范围_____________________.
-3
2
y
x
0
x>2
或
-3<x<0
四、课堂训练
7.如图,过反比例函数
图象上的一点
P,作
PA⊥x
轴于
A.若△POA
的面积为
6,则
k=
.
-12
y
x
O
P
A
五、作业
必做题:教科书习题
26.1
第
5,9
题.
选做题:
如图,直线
y=ax+b
与双曲线
交于两点
A(1,2),B(m,4)两点,
(1)求直线与双曲线的解析式;
(2)求不等式
ax+b
>
的解集.
(3)连接
OA,OB.求△AOB
的面积.
x
y
O
B
A
第二十六章 反比例函数
26.1 反比例函数
26.1.1 反比例函数
一、情景导入
问题
1 京沪线铁路全程为
1
463
km,某次列车的平均速度
v(单位:km/h)随此次列车的全程运行时间
t(单位:h)的变化而变化;
思考:(1)平均速度
v
和时间
t
存在着怎样的关系?
(2)这三者中,谁是常量,谁是变量?
(3)两个变量间具有函数关系吗?
(4)能写出列车的平均速度
v
随此次列车的全程运行时间
t
的函数关系吗?
一、情景导入
问题
2 下列问题中,变量间具有函数关系吗?如果有,请直接写出解析式.
(1)某住宅小区要种植一块面积为
1
000
m2
的矩形草坪,草坪的长
y(单位:m)随宽
x(单位:m)的变化而变化;
一、情景导入
(2)已知北京市的总面积为
1.68×104
km2
,人均占有面积
S(单位:km2
/人)随全市总人口
n(单位:人)的变化而变化.
二、探究新知
,
,
.
思考 这些解析式有什么共同特征?
归纳 上述解析式具有
的形式,其中
k
是非零常数.
二、探究新知
定义:一般地,形如
(k为常数,k≠0)的函数,叫做反比例函数,其中
x
是自变量,y
是函数.
思考:自变量
x
及函数值
y
的取值范围?
x≠0
,y≠0
.
下列函数是不是反比例函数?若是,请指出
k
的值.
二、探究新知
是,
不是
不是
是,
是,
思考:反比例函数的表达形式有哪些?
二、探究新知
二、探究新知
例
1 已知
y
是
x
的反比例函数,并且当
x=2
时,y=6.
(1)写出
y
关于
x
的函数解析式;
(2)当
x=4
时,求
y
的值.
思考:求函数解析式常用方法是什么?
待定系数法.
先设出函数解析式,再根据条件确定解析式中未知数的系数,从而得出函数解析式.
二、探究新知
解:(1)设
因为当
x=2
时,y=6,所以有
解得
k=12.
因此
(2)把
x=4
代入
,得
二、探究新知
方法总结:用待定系数法求反比例函数解析式的一般步骤:①
设出含有待定系数的反比例函数解析式
;
②
将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;③
解方程,求出待定系数;④
写出反比例函数解析式.
二、探究新知
已知
y
与
x+1
成反比例,并且当
x=3
时,y=4.
(1)写出
y
关于
x
的函数解析式;
(2)当
x=7
时,求
y
的值.
解:(1)设
.因为当
x=3
时,y=4,所以有
解得
k=1.
(2)把
x=7
代入
,得
三、课堂小结
用待定系数法求反比例函数解析式
反比例函数
反比例函数
定义
三种表达方式
四、课堂训练
1.下列函数中,y
是
x
的反比例函数的是( ).
A.
B.
C.
D.
A
四、课堂训练
2.生活中有许多反比例函数的例子,在下面的实例中,x
和
y
成反比例函数关系的有( ).
①
x
人共饮水
10
kg,平均每人饮水
y
kg;②
底面半径为
x
m,高为
y
m的圆柱形水桶的体积为
10
m3;③
用铁丝做一个圆,铁丝的长为
x
cm,做成圆的半径为
y
cm;④
在水龙头前放满一桶水,出水的速度为
x,放满一桶水的时间
y.
A.1
个
B.2
个
C.3
个
D.4
个
B
3.填空:
(1)若
是反比例函数,则
m
的取值范围是_____.
(2)若
是反比例函数,则
m
的取值范围是________________
.
(3)若
是反比例函数,则
m
的取值范围是
__________.
m≠0
且
m≠-2
四、课堂训练
m≠1
m=-1
四、课堂训练
4.已知变量
y
与
x
成反比例,且当
x=3
时,y=-4.
(1)写出
y
关于
x
的函数解析式;
(2)当
y=6
时,求
x
的值.
解:(1)设
因为当
x=3
时,y=-4,所以有
解得
k=-12.
因此,y
关于
x
的函数解析式为
四、课堂训练
(2)把
y=6
代入
,得
解得
x=-2.
四、课堂训练
5.小明家离学校
1
000
m,每天他往返于两地之间,有时步行,有时骑车.假设小明每天上学时的平均速度为
v(m/min),所用的时间为
t(min).
(1)求变量
v
和
t
之间的函数关系式;
解:
(t>0).
四、课堂训练
(2)小明星期二步行上学用了
25
min,星期三骑自行车上学用了
8
min,那么他星期三上学时的平均速度比星期二快多少?
解:当
t=25
时,
当
t=8
时,
125-40=85(m/min).
答:他星期三上学时的平均速度比星期二快
85
m/min.
五、作业
必做题:习题
26.1
第
1,2,4
题.
选做题:已知函数
y=y1+y2,且
y1
与
x
成正比例,y2
与
x
成反比例,且当
x=1
时,y=5;当
x=2
时,y=4.
(1)求
y
与
x
的函数关系式.
(2)当
x=-2
时,求函数
y
的值.
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第一课时
一、情景导入
1.什么是反比例函数?
一般地,形如
(k
是常数,k≠0
)的函数叫做反比例函数.
2.反比例函数的定义中需要注意什么?
(1)k
是非零常数.
(2)x≠0,y≠0.
(3)xy=k,y=kx-1
.
3.还记得一次函数的图象与性质吗?
4.还记得二次函数的图象与性质吗?
5.如何画函数的图象?
反比例函数的图象与性质又如何呢?
这节课开始我们来一起探究吧.
一、情景导入
画函数图象的方法
描点法
列
表
描
点
连
线
二、探究新知
我们先研究
k>0
的情形.
例
2 画出反比例函数
和
的函数图象.
温馨提示
列表,描点,连线的注意事项是什么?
x
…
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
…
…
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
…
…
-2
-2.4
-3
-4
-6
-12
12
6
4
3
2.4
2
…
二、探究新知
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
二、探究新知
思考:观察这两个函数图象,回答问题:
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着
x
的增大,y
如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数
(k>0),考虑问题(1)(2),你能得出同样的结论吗?
二、探究新知
归纳:对于反比例函数
,当
k>0
时,
(1)函数图象分别位于第一,三象限内;
(2)在每一个象限内,y
随
x
的增大而减小.
二、探究新知
回顾前面我们利用函数图象,从特殊到一般研究反比例函数
(k>0)的性质的过程,你能用类似的方法研究反比例函数
(k<0)的图象和性质吗?
二、探究新知
画出反比例函数
和
的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
二、探究新知
你能说出反比例函数
(k<0)的性质吗?
归纳
对于反比例函数
当
k<0
时,
(1)函数图象分别位于第二,四象限内;
(2)在每一个象限内,y
随
x
的增大而增大.
反比例函数的图象有两条曲线组成,它是双曲线.
二、探究新知
一般地,反比例函数
的图象是双曲线,它具有以下性质:
(1)当
k
>0
时,
双曲线的两支分别位于第一,第三象限,在每一个象限内,y
随
x
的增大而减小.
(2)当
k
<0
时,
双曲线的两支分别位于第二,第四象限,在每一个象限内,y
随
x
的增大而增大.
二、探究新知
在同一坐标系中反比例函数
与
的图象在位置上有什么关系?
二、探究新知
结论:
当
k
互为相反数时,对应的反比例函数图象既关于
x
轴对称,也关于
y
轴对称.
二、探究新知
1.下列图象中,可以是反比例函数的图象的( ).
A.
B.
C.
D.
D
二、探究新知
2.反比例函数
的图象大致( ).
A.
B.
C.
D.
x
y
o
x
o
y
x
y
o
x
y
o
C
二、探究新知
3.
函数
的图象在第________象限,在每一象限内,y
随
x
的增大而_________.
4.函数
的图象在第________象限,在每一象限内,y
随
x
的增大而_________.
5.函数
当
x>0
时,图象在第____象限,y
随
x
的增大而_________.
一,三
二,四
一
减小
增大
减小
二、探究新知
6.已知点
A(-2,a),B(-1,b),C(3,c)都在反比例函数
图象上,试比较
a,b,c
的大小.
解:把点
A(-2,a),B(-1,b),C(3,c)分别带入函数
中得:
所以
b<a<c.
二、探究新知
另解:因为
k=1>0,所以在每个象限内
y
随
x
的增大而减小,由图知,因为
-2<-1<0,所以
b<a<0,而
c>0,所以
b<a<c.
三、课堂小结
本节课我们学习了哪些知识?
k>0时,在每个象限内,y
随
x
的增大而减小
函数的
增减性
k<0时,在二、四象限
k>0时,在一、三象限
图象为双曲线
k<0时,在每个象限内,y
随
x
的增大而增大
分类讨论
四、课堂训练
6.对于反比例函数
下列说法正确的是( ).
A.其图象经过(2,-1)
B.其图象位于第二,四象限
C.当
x<0
时,y
随
x
值的增大而减小
D.当
x>0
时,y
随
x
值的增大而增大
7.下列反比例函数图象一定在第一,三象限的是( ).
A.
B.
C.
D.
C
C
四、课堂训练
8.甲乙两地相距
100
km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间
y(h)表示为汽车的平均速度
x(km/h)
的函数,则这个函数的图象大致是( ).
A.
B.
C.
D.
C
四、课堂训练
9.函数
y=kx-3
与
(k≠0)在同一坐标系内的图象可能是( ).
A.
B.
C.
D.
B
五、作业
必做题:教科书习题
26.1
第
3,8
题.
选做题:
1.函数
y=kx-k
与
(k≠0)的图象大致是( ).
x
y
O
y
y
x
x
y
O
O
O
x
D
A.
B.
C.
D.
五、作业
2.在同一直角坐标系中,函数
与
y=ax+1(a≠0)的图象可能是( ).
y
x
O
y
x
O
y
x
O
y
x
O
B
A.
B.
C.
D.
第二十六章 反比例函数
26.1 反比例函数
26.1.2 反比例函数的图象和性质
第二课时
一、情景导入
1.什么是反比例函数?
一般地,形如
(k是常数,
k≠0
)的函数叫做反比例函数.
2.反比例函数的图象和性质是什么?
一般地,反比例函数
的图象是双曲线.
(1)当
k>0
时,
双曲线的两支分别位于第一,第三象限,在每一个象限内,y
随
x
的增大而减小.
(2)当
k<0
时,
双曲线的两支分别位于第二,第四象限,在每一个象限内,y
随
x
的增大而增大.
一、情景导入
例
3 已知反比例函数的图象经过点
A(2,6).
(1)这个函数的图象位于哪些象限?y
随
x
的增大如何变化?
(2)
点
B(3,4),C(
),D(2,5)是否在这个函数的图象上?
解:(1)因为点
A
(2,6)
在第一象限,所以这个函数的图象位于第一,三象限,在每一个象限内,y
随
x
的增大而减小.
一、情景导入
(2)设这个反比例函数的解析式为
,因为点
A(2,6)在其图象上,所以点
A
的坐标满足
,即
解得
k=12.
所以这个反比例函数的解析式为
因为点
B,C
的坐标都满足
,点
D
的坐标不满足
,所以点
B,C
在函数
的图象上,点
D
不在这个函数的图象上.
二、探究新知
已知反比例函数
的图象经过点
A(2,3).
(1)求这个函数的表达式;
(2)判断点
B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当
-3<x<-1
时,求
y
的取值范围.
二、探究新知
解:(1)因为反比例函数
的图象经过点
A(2
,3),所以点
A
的坐标满足
即
.
解得
k=6.
所以这个函数的表达式为
(2)分别把点
B,C
的坐标代入
,点
B
的坐标不满足
点
C
的坐标满足
,所以点
B
不在
的图象上,点
C
在这个函数的图象上.
二、探究新知
(3)因为 当
x=-3
时,y=-2;当
x=-1
时,y=-6,且
k>0,
所以 当
x<0
时,y
随
x
的增大而减小.
所以 当
-3<x<-1
时,-6<y<-2.
二、探究新知
例
4 如图,它是反比例函数
图象的一支.根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数
m
的取值范围是什么?
(2)在这个函数图象的某一支上任取点
A(x1,y1)和点
B
(x2,y2).如果
x1>x2,那么
y1
和
y2
有怎样的大小关系?
二、探究新知
解:(1)反比例函数的图象只有两种可能:位于第一,第三象限,或者位于第二,第四象限.因为这个函数的图象的一支位于第一象限,所以另一支必位于第三象限.因为这个函数的图象位于第一,第三象限,所以
m-5>0.
解得
m>5.
(2)因为
m-5>0,所以在这个函数图象
的任一支上,y
都随
x
的增大而减小,因此当
x1>x2
时,
y1<y2
.
O
x
y
二、知识拓展
已知反比例函数
的图象上有两点:A(x1,y1),B
(x2,y2)上,且
x1<x2<0
,那么下列结论正确的是( ).
A.
y1<y2
B.
y1>
y2
C.
y1=y2
D.
y1与y2大小不能确定
A
二、探究新知
如图,在反比例函数
的图象上分别取点
P,Q
向
x
轴,y
轴作垂线,围成面积分别为S1,S2
的矩形.
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
二、探究新知
P(2,2)
Q(4,1)
S1
的值
4
S2
的值
4
S1
与
S2
的关系
S1=S2
猜想
S1,S2
与
k
的关系
S1=S2=k
二、探究新知
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
二、探究新知
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
如果
P,Q
是反比例函数
的图象上任意两点.其它条件不变,那么
S1=S2=k
成立吗?
S1=S2=4=|-4|=k
二、探究新知
归
纳 若点
P
是
图象上的任意一点,作
PA
垂直于
x
轴,作
PB
垂直于
y
轴,矩形
AOBP
的面积与
k
的关系是
S矩形
AOBP=|k|.
二、探究新知
1.如图,反比例函数
的图象上的点
M(1,a),过
M
分别作
y
轴和
x
轴的垂线,垂足是
P,Q;则
a=_____;矩形
OQMP
的面积=__________;△PMO
的面积=_____;△QMO
的面积=_____.
2.若点
P
是反比例函数图象上的一
点,过点
P
分别向
x
轴,y
轴作垂线,垂
足分别为点
M,N,若四边形
PMON
的
面积为
3,则这个反比例函数的关系式是
________________.
2
2
1
1
三、课堂小结
1.反比例函数的图象与性质;
2.反比例函数的图象与性质的简单应用.
四、课堂训练
1.若反比例函数的图象经过点(-3,-4),则函数的图象应该在( ).
A.第一,三象限
B.第一,二象限
C.第二,四象限
D.第三,四象限
2.若点(-2,y1),(-1,y2),(2,y3)在反比例函数
的图象上,则( ).
A.
y1>y2>y3
B.y2>y1>y3
C.
y3>y1>y2
D.y3>y2>y1
A
B
四、课堂训练
3.若点(-2,y1),(-1,y2),(2,y3)在反比例函数
的图象上,则(
).
A.y1>y2>y3
B.y2>y1>y3
C.y>y1>y2
D.y3>y2>y1
4.已知反比例函数
(k
是不为
0
的常数)的图象在第二,四象限,那么一次函数
y=kx-k
的图象经过( ).
A.第一,二,三象限
B.第一,二,四象限
C.第一,三,四象限
D.第二,三,四象限
D
C
四、课堂训练
5.考察函数
的图象,当
x=-2
时,y=_______,
当
x<-2
时,
y
的取值范围是__________;当
y>-1
时,x
的取值范围是________________.
-1
-1<y<0
x<-2
或
x>0
四、课堂训练
6.如图是一次函数
y1=kx+b
和反比例函数
的图象,观察图象写出
y1>y2
时,x
的取值范围_____________________.
-3
2
y
x
0
x>2
或
-3<x<0
四、课堂训练
7.如图,过反比例函数
图象上的一点
P,作
PA⊥x
轴于
A.若△POA
的面积为
6,则
k=
.
-12
y
x
O
P
A
五、作业
必做题:教科书习题
26.1
第
5,9
题.
选做题:
如图,直线
y=ax+b
与双曲线
交于两点
A(1,2),B(m,4)两点,
(1)求直线与双曲线的解析式;
(2)求不等式
ax+b
>
的解集.
(3)连接
OA,OB.求△AOB
的面积.
x
y
O
B
A
