26.2 实际问题与反比例函数课件(共4课时 88张)
文档属性
| 名称 | 26.2 实际问题与反比例函数课件(共4课时 88张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 10:34:41 | ||
图片预览









文档简介
(共88张PPT)
第二十六章 反比例函数
26.2 实际问题与反比例函数
第一课时
一、情景导入
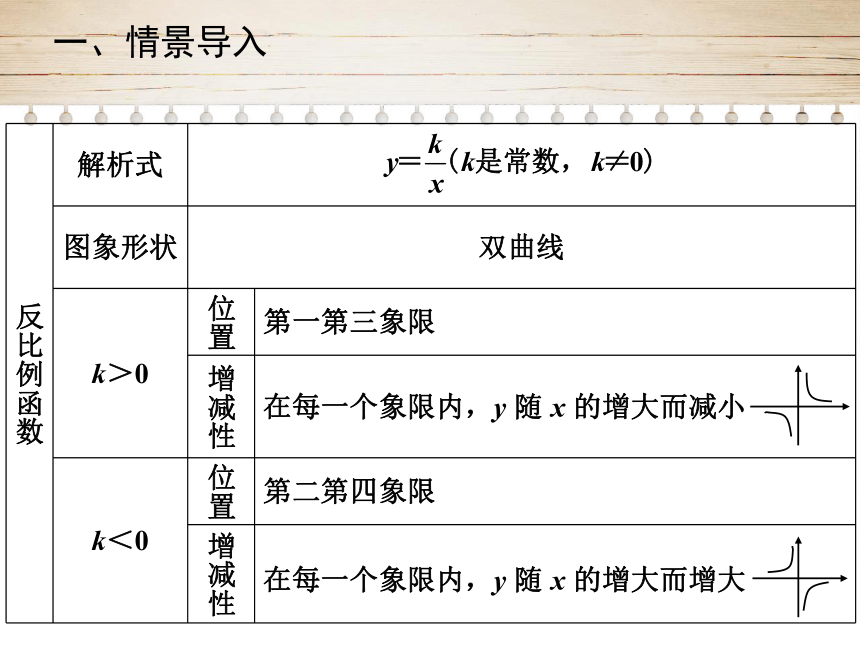
反比例函数
解析式
图象形状
双曲线
k>0
位置
第一第三象限
增减性
在每一个象限内,y
随
x
的增大而减小
k<0
位置
第二第四象限
增减性
在每一个象限内,y
随
x
的增大而增大
一、情景导入
1.函数
的图象在第_______象限,y
随
x
的增大而_______.
2.自行车运动员在长
10
000
米的路程上骑车训练,行使全程所用的时间
t(秒)与行驶的速度
v(米/秒)之间的函数关系式为_________,当行驶的平均速度为
12.5
米/秒时,行驶全程所用的时间为____________.
二,四
增大
800秒
二、探究新知
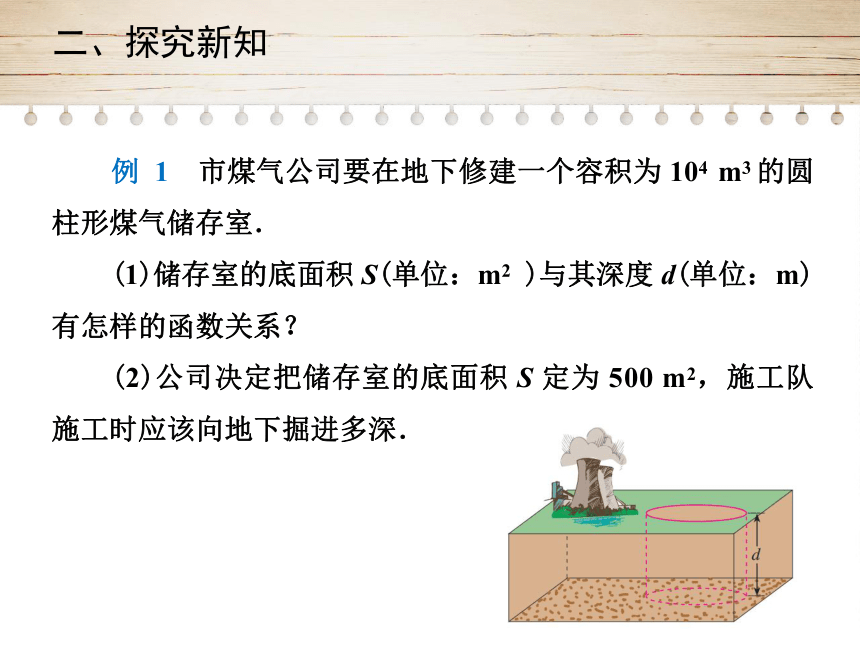
例
1 市煤气公司要在地下修建一个容积为
104
m3
的圆柱形煤气储存室.
(1)储存室的底面积
S(单位:m2
)与其深度
d(单位:m)
有怎样的函数关系?
(2)公司决定把储存室的底面积
S
定为
500
m2,施工队施工时应该向地下掘进多深.
二、探究新知
(3)当施工队按(2)中的计划掘进到地下
15
m
时,公司临时改变计划,把储存室的深度改为
15
m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)
?
思考:圆柱体的体积公式是什么?
圆柱体的体积=圆柱的底面积×圆柱的高
解:(1)根据圆柱的体积公式,得
Sd=104
,
所以
S
关于
d
的函数解析式为
二、探究新知
(2)把
S=500
代入
,得
解得
d=20(m).
如果把储存室的底面积定为
500
m2,施工时应向地下掘进
20
m
深.
二、探究新知
(3)根据题意,把
d=15
代入
,得
解得
S≈666.67(m2).
当储存室的深度为
15
m
时,底面积应改为
666.67
m2.
二、探究新知
1.在体积为
100
的圆柱中,它的底面积
S
与高
h
的函数关系是_________.
2.在面积为
12
的三角形中,它的一边长
y
与这边上的高
x
的函数关系是_________.
二、探究新知
3.已知某矩形的面积为
36
cm2.
(1)矩形的长
y
与宽
x
的函数关系式为______.
(2)当矩形的长为
12
cm
时,其宽为______.
(3)当矩形的宽为
4
cm,其长为______.
3
cm
9
cm
二、探究新知
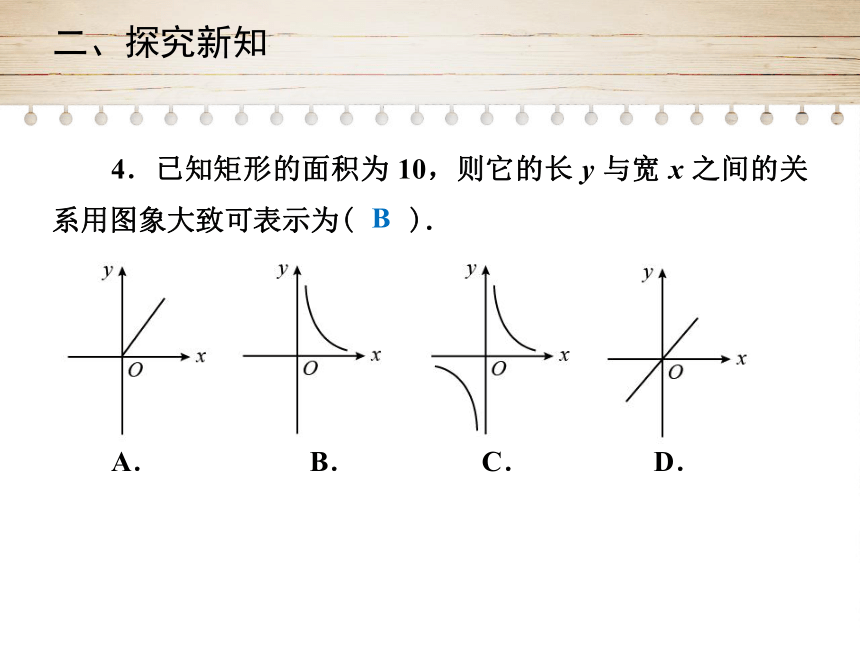
4.已知矩形的面积为
10,则它的长
y
与宽
x
之间的关系用图象大致可表示为( ).
A.
B.
C.
D.
B
二、探究新知
例
2 码头工人每天往一艘轮船上装载
30
吨货物,装载完毕恰好用了
8
天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度
v(单位:吨/天)与卸货天数
t
之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过
5
天卸载完毕,那么平均每天至少要卸载多少吨?
二、探究新知
思考:平均装货速度,装货天数与哪个量有关?
货物的总量.
平均装货速度×装货天数=货物的总量.
货物的总量=30×8.
二、探究新知
解:(1)设轮船上的货物总量为
k
吨,根据已知条件得
k=30×8=240,
所以
v
与
t
的函数式为
二、探究新知
(2)把
t=5
代入
,得
从结果可以看出,如果全部货物恰好用
5
天卸载完,那么平均每天卸载
48
吨.对于函数
,当
t>0
时,t
越小,v
越大.这样若货物不超过
5
天卸载完,则平均每天至少要卸载
48
吨.
方法总结:在解决反比例函数相关的实际问题中,若题目要求“至多”,“至少”,可以利用反比例函数的增减性来解答.
二、探究新知
某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把
1
200
m3
的生活垃圾运走.
(1)若每天能运
x
m3,所需时间为
y
天,则
y
与
x
有怎样的函数关系?
(2)若每辆车一天能运
12
m3,则
5
辆这样的车要用多少天才能运完?
(3)在(2)的情况下,运了
8
天后,剩下的任务要不超过
6
天完成,那么至少需要增加多少辆这样的车?
二、探究新知
解:(1)
(2)x=12×5=60,代入
,得
所以若每辆车一天能运
12
m3,则
5
辆这样的车要用
20天才能运完.
二、探究新知
(3)运了
8
天后剩余的垃圾:1
200-8×60=720(m3),所以
把
y=6
天代入
,得
所以
x=120.
120÷12=10(辆)
,
10-5=5
(辆).
由上可知:剩下的任务要恰好
6
天完成,那么需要增加
5
辆这样的车.对于函数,当
x>0
时,x
越小,y
越大.这样,剩下的任务要不超过
6
天完成,那么每天至少需要运
120
m3
垃圾,也就是至少需要增加
5
辆这样的车.
二、探究新知
例题反思:如何运用反比例函数解决实际问题?
三、课堂小结
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
1.审题;明确常量和变量,找出变量间的数量关系;
2.列出反比例函数解析式;
3.运用反比例函数的图象和性质解决问题.
四、课堂训练
1.判断题(对的在括号内填“√”,错的填“×”).
(1)路程一定时,行驶时间与行驶速度成反比例( )
(2)圆柱体体积一定时,底面积与高成反比例( )
(3)长方形周长一定时,长与宽成反比例( )
(4)圆的面积与半径成反比例( )
√
√
×
×
四、课堂训练
2.面积为
2
的直角三角形一直角边为
x,另一直角边长为
y,则
y
与
x
的变化规律用图象可大致表示为( ).
A.
x
y
1
O
2
x
y
4
O
4
B.
x
y
1
O
4
C.
x
y
1
O
4
1
4
D.
C
四、课堂训练
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为
x,y,剪去部分的面积为
20,若
则
y
与
x
的函数图象是( ).
A
A.
D.
B.
C.
四、课堂训练
4.已知一个长方体的体积是
100
m3,它的长是
y
cm,宽是
5
cm,高是
x
cm.则
y
与
x
的函数关系是_______
;自变量
x
的取值范围是_______
;当
x<4
时,y
的值_______.
5.体积为
20
cm3
的面团做成拉面,
面条的总长度
y(单位:cm)与面条粗细(横截面积)S(单位:cm2)的函数关系为_______,若要使拉出来的面条粗不超过
1
mm2,则面条的总长度应不短于_______
cm.
x>0
>
5
2
000
四、课堂训练
6.司机王某上午驾车从甲地去乙地,他以
80
千米/时的平均速度用
6
小时到达乙地.当他按原路匀速返回时,汽车的速度
v
与时间
t
的函数关系式为_______.若王某必须在
5
小时内回到甲地,那么返程时的平均速度不能小于_________
.
96
千米/时
四、课堂训练
7.如图,某玻璃器皿制造公司要制造一种容积为
1
L
(1
L=1
dm3)的圆锥形漏斗.
(1)漏斗口的面积
S(dm3)与漏斗的深
d(dm)有怎样的函数关系?
(2)如果漏斗的深为
10
cm,那么漏斗口的面积为多少?
(3)如果漏斗口的面积为
60
cm2
,则漏斗的深为多少?
四、课堂训练
解:(1)
(2)10
cm=1
dm,把
d=1
代入解析式,得
S=3,
所以漏斗口的面积为
3
dm2.
(3)60
cm2=0.6
dm2,把
S=0.6
代入解析式,得
d=5.
所以漏斗的深为
5
dm.
五、作业
教科书习题
26.2
第
2,3,7
题.
第二十六章 反比例函数
26.2 实际问题与反比例函数
第二课时
说一说反比例函数的图象与性质
反比例函数
解析式
图象形状
双曲线
k>0
位置
第一第三象限
增减性
在每一个象限内,y
随
x
的增大而减小
k<0
位置
第二第四象限
增减性
在每一个象限内,y
随
x
的增大而增大
一、情景导入
一、情景导入
公元前
3
世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂.
动力
阻力臂
动力臂
阻力
二、探究新知
例
3 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m.
(1)动力
F
与动力臂
l
有怎样的函数关系?当动力臂为
1.5
m
时,撬动石头至少需要多大的力?
(2)若想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长多少?
二、探究新知
解:
(1)根据“杠杆原理”,得
Fl=1
200×0.5,
所以
F
关于
l
的函数解析式为
当
l=1.5
m
时,
对于函数
当
l=1.5
m
时,F=400
N,此时杠杆平衡.因此撬动石头至少需要
400
N
的力.
二、探究新知
(2)对于函数
F
随
l
的增大而减小.因此,只要求出
F=200
N
时对应的
l
的值,就能确定动力臂
l
至少应加长的量.
当
F=400×
=200
时,由
200=
得
3-1.5=1.5
(m).
对于函数
当
l>0
时,l
越大,F
越小.因此,若想用力不超过
400
N
的一半,则动力臂至少要加长
1.5
m.
二、探究新知
思考:在物理中,我们知道,在阻力和阻力臂一定的情况下,动力臂越长就越省力,你能用反比例函数的知识对其进行解释吗?
阻力×阻力臂=动力×动力臂
因为阻力和阻力臂长为大于
0
的定值,动力臂长大于
0,由反比例函数的性质知道,动力随着动力臂的增大而减小.即动力臂越长就越省力.
二、探究新知
假设阿基米德有
500
牛的力,地球的重量约为
6×1025
牛(记为阻力),阻力臂为
2
000
千米,请你帮阿基米德设计该用动力臂为多长的杠杆才能把地球撬动?
解:
2
000
千米=2×106
米,
由已知得F×l=6×1025×2×106=1.2×1032
米,
变形得:
当
F=500
时,l=2.4×1029
米.
故用
2.4×1029
米动力臂的杠杆才能把地球撬动.
二、探究新知
某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地.当人和木板对湿地的压力一定时,随着木板面积
S(m2)的变化,人和木板对地面的压强
p(Pa)也随之变化变化.如果人和木板对湿地地面的压力合计为
600
N,那么:
(1)用含
S
的代数式表示
p,p
是
S
的反比例函数吗?为什么?
(2)当木板面积为
0.2
m2
时,压强是多少?
(3)要求压强不超过
6
000
Pa,木板面积至少要多大?
(4)在直角坐标系中,作出相应的函数图象.
二、探究新知
解:(1)由
,得
p
是
S
的反比例函数,因为对于
S
的每一个确定的值,p
都有唯一确定的值与它对应,根据函数定义和反比例函数的定义,可知
p
是
S
的反比例函数.
(2)当
S=0.2
m2
时,
故当木板面积为
0.2
m2
时,压强是
3
000
Pa.
二、探究新知
(3)当
p=6
000
时,由
得
对于函数
,当
S>0时,S
越大,p
越小.因此,若要求压强不超过
6
000
Pa,木板面积至少要
0.1
m2.
二、探究新知
(4)如图所示.
利用反比例函数解决实际问题时,既要关注函数本身又要考虑实际意义.
0.6
1
000
2
000
0.1
0.5
O
0.3
0.2
0.4
3
000
4
000
5
000
6
000
S/m2
p/Pa
二、探究新知
如果细心观察,你会发现生活中的两个量之间,很多都具有反比例关系,请你举例说明,好吗?
生活中常用的刀具,使用一段时间后就会变钝,用起来很费劲,如果把刀刃磨薄,刀具就会锋利起来.重型坦克,推土机在轮子上安装又宽又长的履带.大型载重卡车装有许多车轮.充满气体的气球用手挤压或者用脚踩会爆.
三、课堂小结
反比例函数在生活实际(物理学科)中的应用.
“杠杆原理”:动力×动力臂=阻力×阻力臂.
压力=压强×受力面积.
①
审题;明确常量和变量,找出变量间的数量关系;
②
列出反比例函数解析式;
③
运用反比例函数的图象和性质解决问题.
注意:
实际问题中的两个变量往往都只能取非负值;作实际问题中的函数图象时,横、纵坐标的单位长度不一定相同.
1.某人对地面的压强与他和地面接触面积的函数关系如图所示.若某一沼泽地地面能承受的压强不超过
300
N/m2,那么此人必须站立在面积为多少的木板上才不至于下陷(木板的重量忽略不计)( ).
A.至少
2
m2
B.至多
2
m2
C.大于
2
m2
D.小于
2
m2
A
四、课堂训练
O
60
20
40
S/m2
p/(N/m2)
四、课堂训练
2.某气球内充满了一定质量的气体,当温度不变时,
气球内气体的气压
p(kPa)是气体体积
V(m3)
的反比例函数,
其图象如图所示,当气球内的气压大于
120
kPa
时,
气球将爆炸.为了安全起见,气球的体积应( ).
A.不大于
B.小于
C.不小于
D.大于
O
60
V/m3
p/kPa
1.6
C
四、课堂训练
3.受条件限制,无法得知撬石头时的阻力,小刚选择了动力臂为
1.2
米的撬棍,用了
500
牛顿的力刚好撬动;小明身体瘦小,只有
300
牛顿的力量,他该选择动力臂为____的撬棍才能撬动这块大石头.
2
米
四、课堂训练
4.某汽车的功率
P
为一定值,汽车行驶时的速度
v(m/s)与它所受的牵引力
F(N)之间的函数关系如下图所示:
(1)这辆汽车的功率是多少?请写出这一函数的解析式;
(2)当它所受牵引力为
1
200
牛时,汽车的速度为多少
km/h?
(3)如果限定汽车的速度不超过
30
m/s,则
F
在什么范围内?
四、课堂训练
解:(1)P=Fv=300×20=6
000.
所以
(2)把
F=1
200
N
代入得
v=50.
50
m/s=180
km/m.
四、课堂训练
(3)把
v=30
代入
得
F=2
000.
对于函数
当
v>0
时,v
越小,F
越大.因此,
如果限定汽车的速度不超过
30
m/s,则
F≥2
000
N.
五、作业
必做题:教科书习题
26.2
第
6
题.
选做题:教科书习题
26.2
第
9
题.
第二十六章 反比例函数
26.2 实际问题与反比例函数
第三课时
一、情景导入
利用反比例函数解决实际问题时,既要关注函数本身又要考虑实际意义.
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
一、情景导入
上节课我们运用了反比例函数知识解决了生活中的一些简单问题,本节课我们继续用反比例函数解决生活中的一些问题.
物理课中我们知道电学中有:用电器的功率
P(单位:W),用电器两端的电压
U(单位:V),用电器的电阻
R
(单位:Ω).这三者有什么关系呢?
二、探究新知
例
4 一个用电器的电阻是可调节的,其范围为
110~220
Ω.已知电压为
220
V,这个用电器的电路图如图所示.
(1)功率
P
与电阻
R
有怎样的函数关系?
(2)这个用电器功率的范围是多少?
U
~
二、探究新知
解:(1)根据电学知识,当
U=220
时,得
①
二、探究新知
(2)根据反比例函数的性质可知,电阻越大,功率越小.把电阻的最小值
R=110
代入
①
式,得到功率的最大值
把电阻的最大值
R=220
代入
①
式,得到功率的最小值
因此用电器功率的范围为
220~440
W.
二、探究新知
思考:结合上例,想一想为什么收音机,台灯的亮度以及电风扇的转速可以调节?
二、探究新知
收音机的音量,台灯的亮度以及电风扇的转速都由用电器的输出功率决定.在电压一定的情况下,用电器的输出功率是用电器电路中电阻的反比例函数.所以调节用电器的电阻的大小,就能调节用电器的输出功率,从而能调节收音机的音量,台灯的亮度以及电风扇的转速.
D
二、探究新知
1.在公式
中,当电压
U
一定时,电流
I
与电阻
R
之间的函数关系可用图象大致表示为( ).
A.
C.
B.
D.
I
R
I
R
I
R
I
R
二、探究新知
2.在某一电路中,保持电压不变,电流
I(安培)和电阻
R(欧姆)成反比例,当电阻
R=5
欧姆时,电流
I=2
安培.
(1)求
I
与
R
之间的函数关系式;
(2)当电流
I=0.5
时,求电阻
R
的值.
二、探究新知
解:
(1)设
因为当电阻
R=5
欧姆时,电流
I=2
安培,所以
U=10.
所以
I
与
R
之间的函数关系式为
(2)当
I=0.5
安培时,
解得
R=20(欧姆).
3.一封闭电路中,电流
I(A)与电阻
R(Ω)之间的函数图象如下图,回答下列问题:
(1)写出电路中电流
I(A)与电阻
R(Ω)之间的函数关系式.
解:(1)设
由图象知,
当电阻
R=3
时,I=2,所以
U=3×2=6.
所以
I
与
R
之间的函数关系式为
O
I/A
3
2
二、探究新知
R/Ω
(2)如果一个用电器的电阻为
5
Ω,其允许通过的最大电流为
1
A,那么把这个用电器接在这个封闭电路中,会不会烧坏?试通过计算说明.
解:(2)当
R=5
时,
>1.
所以这个用电器接在这个封闭电
路中,会烧坏.
二、探究新知
O
I
/A
3
2
R/Ω
二、探究新知
(3)若允许的电流不得超过
4
A
时,那么电阻
R
的取值应控制在什么范围?
解:(3)当
I=4
时,
对于函数
当
R>0
时,R
越大,I
越小.
因此,若允许的电流
不得超过
4
A
时,那么电阻
R
的取值
应不小于
1.5
Ω.
O
I
/A
3
2
R/Ω
三、课堂小结
反比例函数在生活实际(物理学科)中的应用.
①
审题;明确常量和变量,找出变量间的数量关系;
②
列出反比例函数解析式;
③
运用反比例函数的图象和性质解决问题.
A
四、课堂训练
1.当电压为
220
V
时(电压=电流×电阻),通过电路的电流
I(A)与电路中的电阻
R(Ω)之间的函数关系为
( ).
四、课堂训练
5.蓄电池的电压为定值.使用此电源时,电流
I(A)是电阻
R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当
R=10
Ω
时,电流能是
4
A
吗?为什么?
O
9
I(A)
4
R(Ω)
四、课堂训练
解:(1)设
把
M(4,9)代入得
k=4×9=36.
所以这个反比例函数的解析式为
(2)当
R=10
Ω
时,
所以电流不可能是
4
A.
O
9
I(A)
4
R(Ω)
五、作业
必做题:教科书习题
26.2
第
4,8
题.
选做题:
若有两并联用电器电路图如图所示:其中一用电器电阻R1=8.5
Ω,你能想办法得到另一个用电器的电阻
R2
是多少?
小明向老师借了一个电流表,通过测量得出
I1=0.4
A,I2=0.17
A,因此他断言
R2=20
Ω.你能说明他是怎样得出结论的吗?
R1
R2
第二十六章 反比例函数
26.2
实际问题与反比例函数
第四课时
一、情景导入
1.反比例函数的概念
定义:形如_______(k为常数,k≠0)的函数称为反比例函数,其中
x
是自变量,y
是
x
的函数,k
是比例系数.
防错提醒:(1)k≠0;
(2)自变量
x≠0;
(3)函数
y≠0.
一、情景导入
2.反比例函数的图象与性质
图象
所在象限
性质
(k≠0)
k>0
一,三象限(
x,y同号)
在每个象限内,y
随
x
的增大而减小
k<0
二,四象限(
x,y
异号)
在每个象限内,y
随
x
的增大而增大
x
y
o
x
y
o
一、情景导入
实际问题与反比例函数
利用反比例函数解决实际问题时,既要关注
函数本身又要考虑实际意义.
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
二、探究新知
某单位要建一个
200
平方米的矩形草坪,已知它的长是
y
米,宽是
x
米,则
y
与
x
之间的函数关系为________;
当它的宽为
8
米时,则它的长为______.当它的长不小于
20
米时,则它的宽至多为______.
25米
10米
二、探究新知
例 病人按规定的剂量服用某种药物,测得服药后
2小时,每毫升血液中的含药量达到最大值为
4
毫克.
已知服药后
2
小时前每毫升血液中的含药量
y(单位:毫克)与时间
x(单位:小时)成正比例;2
小时后
y
与
x
成反比例(如图).
根据以上信息解答下列问题:
O
y/毫克
x/小时
2
4
二、探究新知
(1)求当
0≤x≤2
时,y与
x的函数解析式;
(2)求当
x>2
时,y
与
x
的函数解析式;
(3)若每毫升血液中的含药量不低于
2
毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
二、探究新知
解:(1)当
0≤x≤2
时,y
与
x
成正比例函数关系.设
y=kx,
由于点(2,4)在线段上,
所以
4=2k.
所以
k=2.
所以
y
与
x
的函数解析式为:y=2x.
二、探究新知
(2)当
x>2
时,y
与
x
成反比例函数关系
设
由于点(2,4)
在反比例函数的图象上,
所以
解得
k=8.
所以当
x>2
时,y
与
x
的函数解析式为
二、探究新知
(3)当
0≤x≤2
时,含药量不低于
2
毫克,
即
2x≥2,
解得
x≥1,
所以
1≤x≤2.
当
x>2
时,含药量不低于
2
毫克,
即
≥2,
解得
x≤4.
所以
2<
x≤4.
4-1=3(小时)
所以服药一次,治疗疾病的有效时间是
3
小时.
二、探究新知
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为
y
℃,从加热开始计算的时间为
x
分钟.据了解,该材料在加热过程中温度
y
与时间
x
成一次函数关系.已知该材料在加热前的温度为
4
℃,加热一段时间使材料温度达到
28
℃时停止加热,停止加热后,
材料温度逐渐下降,这时温度
y
与
时间
x
成反比例函数关系,已知第
12
分钟时,材料温度是
14
℃.
O
y(℃)
x(min)
12
4
14
28
二、探究新知
(1)分别求出该材料加热和停止加热过程中
y
与
x
的函数关系式(写出
x
的取值范围);
(2)根据该食品制作要求,在材料温度不低于
12
℃
的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
二、探究新知
解:
(1)由图知点(12,14)在反比例函数的图象上,
设反比例函数的解析式为
所以
所以
k2=168.所以
当
y=28
时,可求得
x=6.
因此可由图知点(6,28),(0,4)
在一次函数的图象上.
设一次函数的解析式为
y=k1x+b,则
所以
y=4x+4(0≤x≤6).
O
y(℃)
x(min)
12
4
14
28
二、探究新知
(2)当
y=12
时,由
y=4x+4,
解得
x=2.
当
y=12
时,由
解得
x=14.
14-2=12,
所以对该材料进行特殊处理的时间为
12
分钟.
O
y(℃)
x(min)
12
4
14
28
三、课堂小结
本节课学习了哪些内容?应注意什么?
1.反比例函数在生活中的应用(与一次函数结合)
;
2.注意根据自变量的取值范围求函数解析式;
3.根据实际情况,选择不同的函数解析式解决问题.
四、课堂训练
1.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到
800
℃,然后停止煅烧进行锻造操作,经过
8
min
时,材料温度降为
600
℃.煅烧时温度
y(℃)与时间
x(min)成一次函数关系;锻造时,温度
y(℃)与时间
x(min)成反比例函数关系(如图).已知该材料初始温度是
32
℃.
四、课堂训练
(1)分别求出材料煅烧和锻造时
y
与
x
的函数关系式,并且写出自变量
x
的取值范围;
(2)根据工艺要求,当材料温度低于
480
℃
时,须停止操作.那么锻造的操作时间有多长?
解:
(1)
(2)6.5
分钟
四、课堂训练
2.如图,利用一面长
90
m
砖墙,用篱笆围成一个靠墙的矩形园子,园子的预定面积为
180
m2,设园子平行于墙面方向的一边的长度为
x(m),与之相邻的另一边为
y(m).
(1)求
y
关于
x
的函数关系式和自变量
x
的取值范围;
(2)画出这个函数的图象;
(3)若要求围成的园子平行于墙的一边长度不小于墙长的
,求与之相邻的另一边长的取值范围.
y
x
四、课堂训练
解:(1)
(2)图略.但要注意自变量的取值范围.
(3)另一边的长度不多于
3
米且不少于
2
米.
五、作业
必做题:
1.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过
5
min
的集中药物喷洒,再封闭宿舍
10
min,然后打开门窗进行通风,室内每立方米空气中含药量
y(mg/m3)与药物在空气中的持续时间
x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.当室内空气中的含药量低于
2
mg/m3
时,对人体才
是安全的.那么从喷洒药物开始需经过多长
时间学生才能进入室内?
2.画出本章的知识结构图.
五、作业
选做题:
如图,一次函数
y=x+4
的图象与反比例函数(k
为常数且
k≠0)的图象交于
A(-1,a),B
两点,与
x
轴交于点
C.
(1)求此反比例函数的解析式;
(2)若点
P
在
x
轴上,且
S△ACP=S△BOC,求点
P
的坐标.
第二十六章 反比例函数
26.2 实际问题与反比例函数
第一课时
一、情景导入
反比例函数
解析式
图象形状
双曲线
k>0
位置
第一第三象限
增减性
在每一个象限内,y
随
x
的增大而减小
k<0
位置
第二第四象限
增减性
在每一个象限内,y
随
x
的增大而增大
一、情景导入
1.函数
的图象在第_______象限,y
随
x
的增大而_______.
2.自行车运动员在长
10
000
米的路程上骑车训练,行使全程所用的时间
t(秒)与行驶的速度
v(米/秒)之间的函数关系式为_________,当行驶的平均速度为
12.5
米/秒时,行驶全程所用的时间为____________.
二,四
增大
800秒
二、探究新知
例
1 市煤气公司要在地下修建一个容积为
104
m3
的圆柱形煤气储存室.
(1)储存室的底面积
S(单位:m2
)与其深度
d(单位:m)
有怎样的函数关系?
(2)公司决定把储存室的底面积
S
定为
500
m2,施工队施工时应该向地下掘进多深.
二、探究新知
(3)当施工队按(2)中的计划掘进到地下
15
m
时,公司临时改变计划,把储存室的深度改为
15
m.相应地,储存室的底面积应改为多少(结果保留小数点后两位)
?
思考:圆柱体的体积公式是什么?
圆柱体的体积=圆柱的底面积×圆柱的高
解:(1)根据圆柱的体积公式,得
Sd=104
,
所以
S
关于
d
的函数解析式为
二、探究新知
(2)把
S=500
代入
,得
解得
d=20(m).
如果把储存室的底面积定为
500
m2,施工时应向地下掘进
20
m
深.
二、探究新知
(3)根据题意,把
d=15
代入
,得
解得
S≈666.67(m2).
当储存室的深度为
15
m
时,底面积应改为
666.67
m2.
二、探究新知
1.在体积为
100
的圆柱中,它的底面积
S
与高
h
的函数关系是_________.
2.在面积为
12
的三角形中,它的一边长
y
与这边上的高
x
的函数关系是_________.
二、探究新知
3.已知某矩形的面积为
36
cm2.
(1)矩形的长
y
与宽
x
的函数关系式为______.
(2)当矩形的长为
12
cm
时,其宽为______.
(3)当矩形的宽为
4
cm,其长为______.
3
cm
9
cm
二、探究新知
4.已知矩形的面积为
10,则它的长
y
与宽
x
之间的关系用图象大致可表示为( ).
A.
B.
C.
D.
B
二、探究新知
例
2 码头工人每天往一艘轮船上装载
30
吨货物,装载完毕恰好用了
8
天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度
v(单位:吨/天)与卸货天数
t
之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过
5
天卸载完毕,那么平均每天至少要卸载多少吨?
二、探究新知
思考:平均装货速度,装货天数与哪个量有关?
货物的总量.
平均装货速度×装货天数=货物的总量.
货物的总量=30×8.
二、探究新知
解:(1)设轮船上的货物总量为
k
吨,根据已知条件得
k=30×8=240,
所以
v
与
t
的函数式为
二、探究新知
(2)把
t=5
代入
,得
从结果可以看出,如果全部货物恰好用
5
天卸载完,那么平均每天卸载
48
吨.对于函数
,当
t>0
时,t
越小,v
越大.这样若货物不超过
5
天卸载完,则平均每天至少要卸载
48
吨.
方法总结:在解决反比例函数相关的实际问题中,若题目要求“至多”,“至少”,可以利用反比例函数的增减性来解答.
二、探究新知
某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把
1
200
m3
的生活垃圾运走.
(1)若每天能运
x
m3,所需时间为
y
天,则
y
与
x
有怎样的函数关系?
(2)若每辆车一天能运
12
m3,则
5
辆这样的车要用多少天才能运完?
(3)在(2)的情况下,运了
8
天后,剩下的任务要不超过
6
天完成,那么至少需要增加多少辆这样的车?
二、探究新知
解:(1)
(2)x=12×5=60,代入
,得
所以若每辆车一天能运
12
m3,则
5
辆这样的车要用
20天才能运完.
二、探究新知
(3)运了
8
天后剩余的垃圾:1
200-8×60=720(m3),所以
把
y=6
天代入
,得
所以
x=120.
120÷12=10(辆)
,
10-5=5
(辆).
由上可知:剩下的任务要恰好
6
天完成,那么需要增加
5
辆这样的车.对于函数,当
x>0
时,x
越小,y
越大.这样,剩下的任务要不超过
6
天完成,那么每天至少需要运
120
m3
垃圾,也就是至少需要增加
5
辆这样的车.
二、探究新知
例题反思:如何运用反比例函数解决实际问题?
三、课堂小结
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
1.审题;明确常量和变量,找出变量间的数量关系;
2.列出反比例函数解析式;
3.运用反比例函数的图象和性质解决问题.
四、课堂训练
1.判断题(对的在括号内填“√”,错的填“×”).
(1)路程一定时,行驶时间与行驶速度成反比例( )
(2)圆柱体体积一定时,底面积与高成反比例( )
(3)长方形周长一定时,长与宽成反比例( )
(4)圆的面积与半径成反比例( )
√
√
×
×
四、课堂训练
2.面积为
2
的直角三角形一直角边为
x,另一直角边长为
y,则
y
与
x
的变化规律用图象可大致表示为( ).
A.
x
y
1
O
2
x
y
4
O
4
B.
x
y
1
O
4
C.
x
y
1
O
4
1
4
D.
C
四、课堂训练
3.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为
x,y,剪去部分的面积为
20,若
则
y
与
x
的函数图象是( ).
A
A.
D.
B.
C.
四、课堂训练
4.已知一个长方体的体积是
100
m3,它的长是
y
cm,宽是
5
cm,高是
x
cm.则
y
与
x
的函数关系是_______
;自变量
x
的取值范围是_______
;当
x<4
时,y
的值_______.
5.体积为
20
cm3
的面团做成拉面,
面条的总长度
y(单位:cm)与面条粗细(横截面积)S(单位:cm2)的函数关系为_______,若要使拉出来的面条粗不超过
1
mm2,则面条的总长度应不短于_______
cm.
x>0
>
5
2
000
四、课堂训练
6.司机王某上午驾车从甲地去乙地,他以
80
千米/时的平均速度用
6
小时到达乙地.当他按原路匀速返回时,汽车的速度
v
与时间
t
的函数关系式为_______.若王某必须在
5
小时内回到甲地,那么返程时的平均速度不能小于_________
.
96
千米/时
四、课堂训练
7.如图,某玻璃器皿制造公司要制造一种容积为
1
L
(1
L=1
dm3)的圆锥形漏斗.
(1)漏斗口的面积
S(dm3)与漏斗的深
d(dm)有怎样的函数关系?
(2)如果漏斗的深为
10
cm,那么漏斗口的面积为多少?
(3)如果漏斗口的面积为
60
cm2
,则漏斗的深为多少?
四、课堂训练
解:(1)
(2)10
cm=1
dm,把
d=1
代入解析式,得
S=3,
所以漏斗口的面积为
3
dm2.
(3)60
cm2=0.6
dm2,把
S=0.6
代入解析式,得
d=5.
所以漏斗的深为
5
dm.
五、作业
教科书习题
26.2
第
2,3,7
题.
第二十六章 反比例函数
26.2 实际问题与反比例函数
第二课时
说一说反比例函数的图象与性质
反比例函数
解析式
图象形状
双曲线
k>0
位置
第一第三象限
增减性
在每一个象限内,y
随
x
的增大而减小
k<0
位置
第二第四象限
增减性
在每一个象限内,y
随
x
的增大而增大
一、情景导入
一、情景导入
公元前
3
世纪,古希腊科学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡.后来人们把它归纳为“杠杆原理”.通俗地说,杠杆原理为:
阻力×阻力臂=动力×动力臂.
动力
阻力臂
动力臂
阻力
二、探究新知
例
3 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m.
(1)动力
F
与动力臂
l
有怎样的函数关系?当动力臂为
1.5
m
时,撬动石头至少需要多大的力?
(2)若想使动力
F
不超过题(1)中所用力的一半,则动力臂
l
至少要加长多少?
二、探究新知
解:
(1)根据“杠杆原理”,得
Fl=1
200×0.5,
所以
F
关于
l
的函数解析式为
当
l=1.5
m
时,
对于函数
当
l=1.5
m
时,F=400
N,此时杠杆平衡.因此撬动石头至少需要
400
N
的力.
二、探究新知
(2)对于函数
F
随
l
的增大而减小.因此,只要求出
F=200
N
时对应的
l
的值,就能确定动力臂
l
至少应加长的量.
当
F=400×
=200
时,由
200=
得
3-1.5=1.5
(m).
对于函数
当
l>0
时,l
越大,F
越小.因此,若想用力不超过
400
N
的一半,则动力臂至少要加长
1.5
m.
二、探究新知
思考:在物理中,我们知道,在阻力和阻力臂一定的情况下,动力臂越长就越省力,你能用反比例函数的知识对其进行解释吗?
阻力×阻力臂=动力×动力臂
因为阻力和阻力臂长为大于
0
的定值,动力臂长大于
0,由反比例函数的性质知道,动力随着动力臂的增大而减小.即动力臂越长就越省力.
二、探究新知
假设阿基米德有
500
牛的力,地球的重量约为
6×1025
牛(记为阻力),阻力臂为
2
000
千米,请你帮阿基米德设计该用动力臂为多长的杠杆才能把地球撬动?
解:
2
000
千米=2×106
米,
由已知得F×l=6×1025×2×106=1.2×1032
米,
变形得:
当
F=500
时,l=2.4×1029
米.
故用
2.4×1029
米动力臂的杠杆才能把地球撬动.
二、探究新知
某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地.当人和木板对湿地的压力一定时,随着木板面积
S(m2)的变化,人和木板对地面的压强
p(Pa)也随之变化变化.如果人和木板对湿地地面的压力合计为
600
N,那么:
(1)用含
S
的代数式表示
p,p
是
S
的反比例函数吗?为什么?
(2)当木板面积为
0.2
m2
时,压强是多少?
(3)要求压强不超过
6
000
Pa,木板面积至少要多大?
(4)在直角坐标系中,作出相应的函数图象.
二、探究新知
解:(1)由
,得
p
是
S
的反比例函数,因为对于
S
的每一个确定的值,p
都有唯一确定的值与它对应,根据函数定义和反比例函数的定义,可知
p
是
S
的反比例函数.
(2)当
S=0.2
m2
时,
故当木板面积为
0.2
m2
时,压强是
3
000
Pa.
二、探究新知
(3)当
p=6
000
时,由
得
对于函数
,当
S>0时,S
越大,p
越小.因此,若要求压强不超过
6
000
Pa,木板面积至少要
0.1
m2.
二、探究新知
(4)如图所示.
利用反比例函数解决实际问题时,既要关注函数本身又要考虑实际意义.
0.6
1
000
2
000
0.1
0.5
O
0.3
0.2
0.4
3
000
4
000
5
000
6
000
S/m2
p/Pa
二、探究新知
如果细心观察,你会发现生活中的两个量之间,很多都具有反比例关系,请你举例说明,好吗?
生活中常用的刀具,使用一段时间后就会变钝,用起来很费劲,如果把刀刃磨薄,刀具就会锋利起来.重型坦克,推土机在轮子上安装又宽又长的履带.大型载重卡车装有许多车轮.充满气体的气球用手挤压或者用脚踩会爆.
三、课堂小结
反比例函数在生活实际(物理学科)中的应用.
“杠杆原理”:动力×动力臂=阻力×阻力臂.
压力=压强×受力面积.
①
审题;明确常量和变量,找出变量间的数量关系;
②
列出反比例函数解析式;
③
运用反比例函数的图象和性质解决问题.
注意:
实际问题中的两个变量往往都只能取非负值;作实际问题中的函数图象时,横、纵坐标的单位长度不一定相同.
1.某人对地面的压强与他和地面接触面积的函数关系如图所示.若某一沼泽地地面能承受的压强不超过
300
N/m2,那么此人必须站立在面积为多少的木板上才不至于下陷(木板的重量忽略不计)( ).
A.至少
2
m2
B.至多
2
m2
C.大于
2
m2
D.小于
2
m2
A
四、课堂训练
O
60
20
40
S/m2
p/(N/m2)
四、课堂训练
2.某气球内充满了一定质量的气体,当温度不变时,
气球内气体的气压
p(kPa)是气体体积
V(m3)
的反比例函数,
其图象如图所示,当气球内的气压大于
120
kPa
时,
气球将爆炸.为了安全起见,气球的体积应( ).
A.不大于
B.小于
C.不小于
D.大于
O
60
V/m3
p/kPa
1.6
C
四、课堂训练
3.受条件限制,无法得知撬石头时的阻力,小刚选择了动力臂为
1.2
米的撬棍,用了
500
牛顿的力刚好撬动;小明身体瘦小,只有
300
牛顿的力量,他该选择动力臂为____的撬棍才能撬动这块大石头.
2
米
四、课堂训练
4.某汽车的功率
P
为一定值,汽车行驶时的速度
v(m/s)与它所受的牵引力
F(N)之间的函数关系如下图所示:
(1)这辆汽车的功率是多少?请写出这一函数的解析式;
(2)当它所受牵引力为
1
200
牛时,汽车的速度为多少
km/h?
(3)如果限定汽车的速度不超过
30
m/s,则
F
在什么范围内?
四、课堂训练
解:(1)P=Fv=300×20=6
000.
所以
(2)把
F=1
200
N
代入得
v=50.
50
m/s=180
km/m.
四、课堂训练
(3)把
v=30
代入
得
F=2
000.
对于函数
当
v>0
时,v
越小,F
越大.因此,
如果限定汽车的速度不超过
30
m/s,则
F≥2
000
N.
五、作业
必做题:教科书习题
26.2
第
6
题.
选做题:教科书习题
26.2
第
9
题.
第二十六章 反比例函数
26.2 实际问题与反比例函数
第三课时
一、情景导入
利用反比例函数解决实际问题时,既要关注函数本身又要考虑实际意义.
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
一、情景导入
上节课我们运用了反比例函数知识解决了生活中的一些简单问题,本节课我们继续用反比例函数解决生活中的一些问题.
物理课中我们知道电学中有:用电器的功率
P(单位:W),用电器两端的电压
U(单位:V),用电器的电阻
R
(单位:Ω).这三者有什么关系呢?
二、探究新知
例
4 一个用电器的电阻是可调节的,其范围为
110~220
Ω.已知电压为
220
V,这个用电器的电路图如图所示.
(1)功率
P
与电阻
R
有怎样的函数关系?
(2)这个用电器功率的范围是多少?
U
~
二、探究新知
解:(1)根据电学知识,当
U=220
时,得
①
二、探究新知
(2)根据反比例函数的性质可知,电阻越大,功率越小.把电阻的最小值
R=110
代入
①
式,得到功率的最大值
把电阻的最大值
R=220
代入
①
式,得到功率的最小值
因此用电器功率的范围为
220~440
W.
二、探究新知
思考:结合上例,想一想为什么收音机,台灯的亮度以及电风扇的转速可以调节?
二、探究新知
收音机的音量,台灯的亮度以及电风扇的转速都由用电器的输出功率决定.在电压一定的情况下,用电器的输出功率是用电器电路中电阻的反比例函数.所以调节用电器的电阻的大小,就能调节用电器的输出功率,从而能调节收音机的音量,台灯的亮度以及电风扇的转速.
D
二、探究新知
1.在公式
中,当电压
U
一定时,电流
I
与电阻
R
之间的函数关系可用图象大致表示为( ).
A.
C.
B.
D.
I
R
I
R
I
R
I
R
二、探究新知
2.在某一电路中,保持电压不变,电流
I(安培)和电阻
R(欧姆)成反比例,当电阻
R=5
欧姆时,电流
I=2
安培.
(1)求
I
与
R
之间的函数关系式;
(2)当电流
I=0.5
时,求电阻
R
的值.
二、探究新知
解:
(1)设
因为当电阻
R=5
欧姆时,电流
I=2
安培,所以
U=10.
所以
I
与
R
之间的函数关系式为
(2)当
I=0.5
安培时,
解得
R=20(欧姆).
3.一封闭电路中,电流
I(A)与电阻
R(Ω)之间的函数图象如下图,回答下列问题:
(1)写出电路中电流
I(A)与电阻
R(Ω)之间的函数关系式.
解:(1)设
由图象知,
当电阻
R=3
时,I=2,所以
U=3×2=6.
所以
I
与
R
之间的函数关系式为
O
I/A
3
2
二、探究新知
R/Ω
(2)如果一个用电器的电阻为
5
Ω,其允许通过的最大电流为
1
A,那么把这个用电器接在这个封闭电路中,会不会烧坏?试通过计算说明.
解:(2)当
R=5
时,
>1.
所以这个用电器接在这个封闭电
路中,会烧坏.
二、探究新知
O
I
/A
3
2
R/Ω
二、探究新知
(3)若允许的电流不得超过
4
A
时,那么电阻
R
的取值应控制在什么范围?
解:(3)当
I=4
时,
对于函数
当
R>0
时,R
越大,I
越小.
因此,若允许的电流
不得超过
4
A
时,那么电阻
R
的取值
应不小于
1.5
Ω.
O
I
/A
3
2
R/Ω
三、课堂小结
反比例函数在生活实际(物理学科)中的应用.
①
审题;明确常量和变量,找出变量间的数量关系;
②
列出反比例函数解析式;
③
运用反比例函数的图象和性质解决问题.
A
四、课堂训练
1.当电压为
220
V
时(电压=电流×电阻),通过电路的电流
I(A)与电路中的电阻
R(Ω)之间的函数关系为
( ).
四、课堂训练
5.蓄电池的电压为定值.使用此电源时,电流
I(A)是电阻
R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当
R=10
Ω
时,电流能是
4
A
吗?为什么?
O
9
I(A)
4
R(Ω)
四、课堂训练
解:(1)设
把
M(4,9)代入得
k=4×9=36.
所以这个反比例函数的解析式为
(2)当
R=10
Ω
时,
所以电流不可能是
4
A.
O
9
I(A)
4
R(Ω)
五、作业
必做题:教科书习题
26.2
第
4,8
题.
选做题:
若有两并联用电器电路图如图所示:其中一用电器电阻R1=8.5
Ω,你能想办法得到另一个用电器的电阻
R2
是多少?
小明向老师借了一个电流表,通过测量得出
I1=0.4
A,I2=0.17
A,因此他断言
R2=20
Ω.你能说明他是怎样得出结论的吗?
R1
R2
第二十六章 反比例函数
26.2
实际问题与反比例函数
第四课时
一、情景导入
1.反比例函数的概念
定义:形如_______(k为常数,k≠0)的函数称为反比例函数,其中
x
是自变量,y
是
x
的函数,k
是比例系数.
防错提醒:(1)k≠0;
(2)自变量
x≠0;
(3)函数
y≠0.
一、情景导入
2.反比例函数的图象与性质
图象
所在象限
性质
(k≠0)
k>0
一,三象限(
x,y同号)
在每个象限内,y
随
x
的增大而减小
k<0
二,四象限(
x,y
异号)
在每个象限内,y
随
x
的增大而增大
x
y
o
x
y
o
一、情景导入
实际问题与反比例函数
利用反比例函数解决实际问题时,既要关注
函数本身又要考虑实际意义.
现实世界中的反比例函数
实际应用
归纳
抽象
反比例函数
的图象和性质
二、探究新知
某单位要建一个
200
平方米的矩形草坪,已知它的长是
y
米,宽是
x
米,则
y
与
x
之间的函数关系为________;
当它的宽为
8
米时,则它的长为______.当它的长不小于
20
米时,则它的宽至多为______.
25米
10米
二、探究新知
例 病人按规定的剂量服用某种药物,测得服药后
2小时,每毫升血液中的含药量达到最大值为
4
毫克.
已知服药后
2
小时前每毫升血液中的含药量
y(单位:毫克)与时间
x(单位:小时)成正比例;2
小时后
y
与
x
成反比例(如图).
根据以上信息解答下列问题:
O
y/毫克
x/小时
2
4
二、探究新知
(1)求当
0≤x≤2
时,y与
x的函数解析式;
(2)求当
x>2
时,y
与
x
的函数解析式;
(3)若每毫升血液中的含药量不低于
2
毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
二、探究新知
解:(1)当
0≤x≤2
时,y
与
x
成正比例函数关系.设
y=kx,
由于点(2,4)在线段上,
所以
4=2k.
所以
k=2.
所以
y
与
x
的函数解析式为:y=2x.
二、探究新知
(2)当
x>2
时,y
与
x
成反比例函数关系
设
由于点(2,4)
在反比例函数的图象上,
所以
解得
k=8.
所以当
x>2
时,y
与
x
的函数解析式为
二、探究新知
(3)当
0≤x≤2
时,含药量不低于
2
毫克,
即
2x≥2,
解得
x≥1,
所以
1≤x≤2.
当
x>2
时,含药量不低于
2
毫克,
即
≥2,
解得
x≤4.
所以
2<
x≤4.
4-1=3(小时)
所以服药一次,治疗疾病的有效时间是
3
小时.
二、探究新知
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为
y
℃,从加热开始计算的时间为
x
分钟.据了解,该材料在加热过程中温度
y
与时间
x
成一次函数关系.已知该材料在加热前的温度为
4
℃,加热一段时间使材料温度达到
28
℃时停止加热,停止加热后,
材料温度逐渐下降,这时温度
y
与
时间
x
成反比例函数关系,已知第
12
分钟时,材料温度是
14
℃.
O
y(℃)
x(min)
12
4
14
28
二、探究新知
(1)分别求出该材料加热和停止加热过程中
y
与
x
的函数关系式(写出
x
的取值范围);
(2)根据该食品制作要求,在材料温度不低于
12
℃
的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
二、探究新知
解:
(1)由图知点(12,14)在反比例函数的图象上,
设反比例函数的解析式为
所以
所以
k2=168.所以
当
y=28
时,可求得
x=6.
因此可由图知点(6,28),(0,4)
在一次函数的图象上.
设一次函数的解析式为
y=k1x+b,则
所以
y=4x+4(0≤x≤6).
O
y(℃)
x(min)
12
4
14
28
二、探究新知
(2)当
y=12
时,由
y=4x+4,
解得
x=2.
当
y=12
时,由
解得
x=14.
14-2=12,
所以对该材料进行特殊处理的时间为
12
分钟.
O
y(℃)
x(min)
12
4
14
28
三、课堂小结
本节课学习了哪些内容?应注意什么?
1.反比例函数在生活中的应用(与一次函数结合)
;
2.注意根据自变量的取值范围求函数解析式;
3.根据实际情况,选择不同的函数解析式解决问题.
四、课堂训练
1.工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到
800
℃,然后停止煅烧进行锻造操作,经过
8
min
时,材料温度降为
600
℃.煅烧时温度
y(℃)与时间
x(min)成一次函数关系;锻造时,温度
y(℃)与时间
x(min)成反比例函数关系(如图).已知该材料初始温度是
32
℃.
四、课堂训练
(1)分别求出材料煅烧和锻造时
y
与
x
的函数关系式,并且写出自变量
x
的取值范围;
(2)根据工艺要求,当材料温度低于
480
℃
时,须停止操作.那么锻造的操作时间有多长?
解:
(1)
(2)6.5
分钟
四、课堂训练
2.如图,利用一面长
90
m
砖墙,用篱笆围成一个靠墙的矩形园子,园子的预定面积为
180
m2,设园子平行于墙面方向的一边的长度为
x(m),与之相邻的另一边为
y(m).
(1)求
y
关于
x
的函数关系式和自变量
x
的取值范围;
(2)画出这个函数的图象;
(3)若要求围成的园子平行于墙的一边长度不小于墙长的
,求与之相邻的另一边长的取值范围.
y
x
四、课堂训练
解:(1)
(2)图略.但要注意自变量的取值范围.
(3)另一边的长度不多于
3
米且不少于
2
米.
五、作业
必做题:
1.春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过
5
min
的集中药物喷洒,再封闭宿舍
10
min,然后打开门窗进行通风,室内每立方米空气中含药量
y(mg/m3)与药物在空气中的持续时间
x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.当室内空气中的含药量低于
2
mg/m3
时,对人体才
是安全的.那么从喷洒药物开始需经过多长
时间学生才能进入室内?
2.画出本章的知识结构图.
五、作业
选做题:
如图,一次函数
y=x+4
的图象与反比例函数(k
为常数且
k≠0)的图象交于
A(-1,a),B
两点,与
x
轴交于点
C.
(1)求此反比例函数的解析式;
(2)若点
P
在
x
轴上,且
S△ACP=S△BOC,求点
P
的坐标.
