人教版九年级下册 第二十七章 相似 27.1 图形的相似课件(共50张)
文档属性
| 名称 | 人教版九年级下册 第二十七章 相似 27.1 图形的相似课件(共50张) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览









文档简介
(共50张PPT)
第二十七章 相似
27.1 图形的相似
第一课时
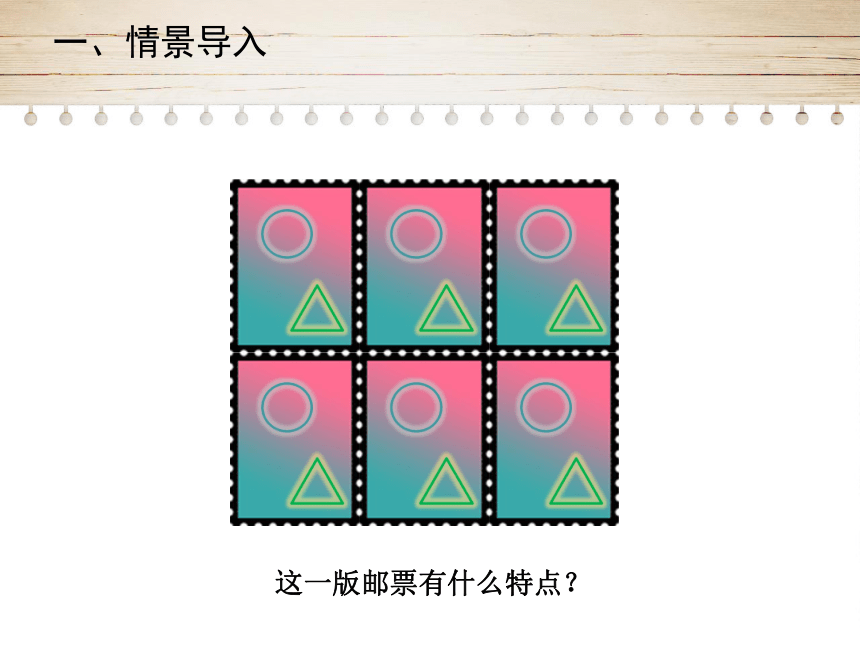
这一版邮票有什么特点?
一、情景导入
一、情景导入
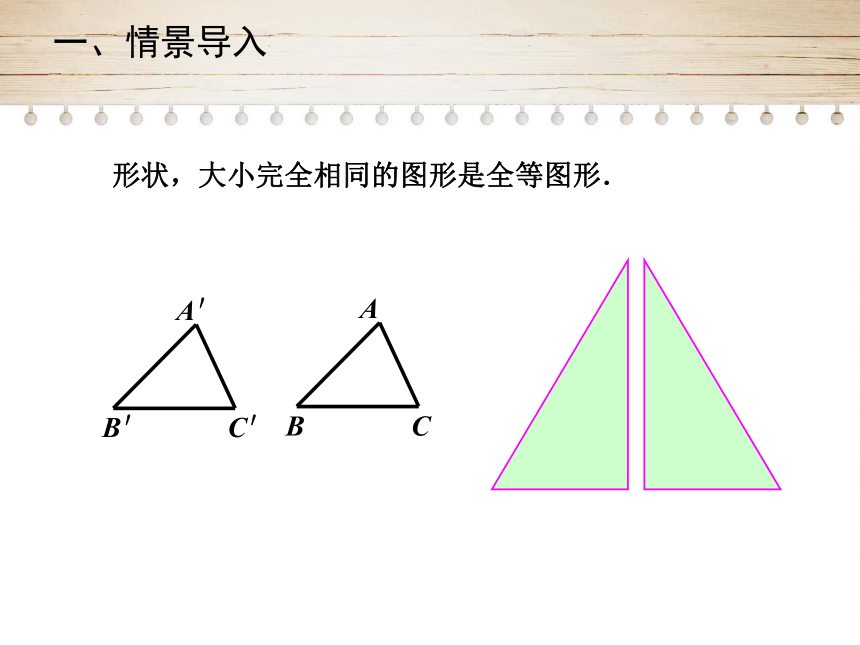
形状,大小完全相同的图形是全等图形.
C′
A′
B′
C
A
B
圣诞老人的
2
寸照片和
4
寸照片,他的形状改变了吗?大小呢?
一、情景导入
一、情景导入
符合国家标准的两面共青团团旗的形状相同吗?大小呢?
二、探究新知
你能来归归类吗?
二、探究新知
下面的“猫咪”有什么相同和不同的地方?
二、探究新知
相同点:形状相同
不同点:大小不相同
归纳:
形状相同的图形叫做相似图形.
相似图形的大小不一定相同.
二、探究新知
图形的放大
二、探究新知
两个图形相似 图形的缩小
二、探究新知
相似图形的关系
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
二、探究新知
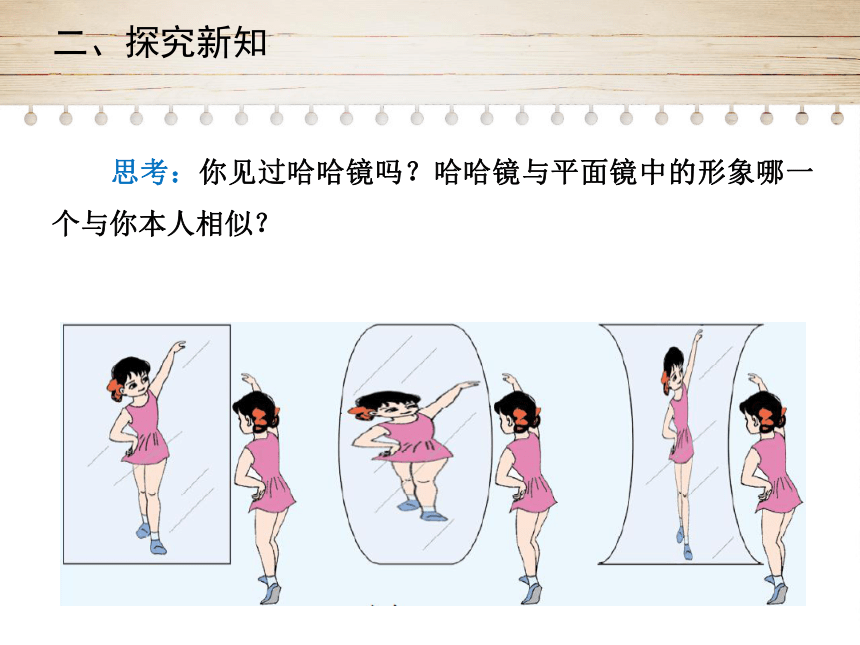
思考:你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
二、探究新知
放大镜下的图形和原来的图形相似吗?
放大镜下的角与原图形中角是什么关系?
三、课堂小结
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
四、课堂训练
1.下面的各组图形中,不相似的一组是( ).
A.
B.
C.
D.
D
四、课堂训练
2.下面每组图形中的两个图形,不是相似图形的是( ).
A.
B.
C.
D.
D
3.观察下面每组的每个图形,相似图形是( ).
A.
B.
C.
D.
四、课堂训练
A
四、课堂训练
4.下列说法不一定正确的是( ).
A.所有的矩形都相似
B.有一个角是
100°的两个等腰三角形相似
C.所有的圆都相似
D.所有的正方形都相似
A
四、课堂训练
5.如图,指出形状相同的图形.
解:(1)与(9);(2)与(11);
(3)与(6);(4)与(7);(5)与(12);
(8)与(10).
四、课堂训练
6.已知下列四种图形:
①
有一个角为直角的菱形;②
邻边相等的矩形;③
对角线相等且互相垂直的四边形;④
四边相等,四角也相等的四边形.剔除其中的一种图形,其余的三种图形形状相同,则剔除的应该是( ).
A.①
B.②
C.③
D.④
C
四、课堂训练
7.下列四组图形中,两个图形相似的有( ).
A.1
组
B.2
组
C.3
组
D.4
组
D
五、作业
教科书习题
27.
1
第
1,4
题.
第二十七章 相似
27.1 图形的相似
第二课时
一、情景导入
多边形
ABCDEF
是显示在电脑屏幕上的,而多边形
A1B1C1D1E1F1
是投射到银幕上的.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
一、情景导入
问题
1 这两个多边形相似吗?
问题
2 在这两个多边形中,是否有对应相等的内角?
问题
3 在这两个多边形中,夹相等内角的两边否成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
二、探究新知
对应角有什么关系?对应边有什么关系?
∠A=∠A1,∠B=∠B1,∠C=∠C1 对应角相等
AB=BC=AC,A1B1=B1C1=A1C1,
AB∶A1B1=BC∶B1C1
=CD∶C1D1,对应边成比例
A
B
C
正三角形
缩小
60°
A
B
C
60°
二、探究新知
对应角有什么关系?
正八边形
∠A=∠A1,∠A=∠A1,∠C=∠C1
,
∠D=∠D1,∠E=∠E1,∠F=∠F1
,对应角相等
150°
A
B
C
F
E
D
放大
150°
A1
B1
C1
F1
E1
D1
二、探究新知
对应边有什么关系?
正八边形
AB=BC=CD=DE=EF=FA,
A1B1=B1C1=C1D1=D1E1=E1F1=F1A1,
AB∶A1B1=BC∶B1C1=CD∶C1D1=DE∶D1E1=EF∶E1F1,
对应边成比例
150°
A
B
C
F
E
D
放大
150°
A1
B1
C1
F1
E1
D1
二、探究新知
相似多边形
对应角相等,对应边成比例.
相似比
相似多边形对应边的比.(k>0)
若相似比
k=1,相似图形有什么关系?
二、探究新知
当相似比
k=1
时,相似图形即是全等图形.
全等是一种特殊的相似.
二、探究新知
各对应角相等,各对应边成比例的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
二、探究新知
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正
n
边形呢?
分析:已知等边三角形的每个角都为
60°,三边都相等.所以满足边数相等,对应角相等,以及对应边的比相等.
a1
a2
a3
an
……
二、探究新知
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
……
a1
a2
a3
an
二、探究新知
思考:任意的两个菱形(或矩形)是否相似?为什么?
二、探究新知
两个多边形相似的条件:
对应角相等,对应边成比例.
二、探究新知
例
1 如图,四边形
ABCD
和
EFGH
相似,求角
α,β
的大小和
EH
的长度
x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
二、探究新知
解:因为四边形
ABCD
和
EFGH
相似,所以它们的对应角相等,由此可得
α=∠C=83°,∠A=∠E=118°.
在四边形
ABCD
中,
β=360°-(78°+83°+118°)=81
°.
二、探究新知
因为四边形
ABCD
和
EFGH
相似,所以它们的对应边成比例,由此可得
解得
x=28
cm.
二、探究新知
例
2 如图所示的两个五边形相似,求未知边
a,b,c,d
的长度.
5
3
2
c
d
7.5
b
a
6
9
二、探究新知
解:相似多边形的对应边的比相等,由此可得
解得:
a=3,b=4.5,c=4,d=6.
所以未知边
a,b,c,d
的长度分别为
3,4.5,4,6.
三、课堂小结
相似多边形对应边的比叫做相似比.
对应角相等,对应边成比例.
相似多边形
ABDF
四、课堂训练
1.下列图形中能够确定相似的是(
).
A.两个半径不相等的圆
B.所有的等边三角形
C.所有的等腰三角形
D.所有的正方形
E.所有的等腰梯形
F.所有的正六边形
四、课堂训练
2.若一张地图的比例尺是
1∶150
000,在地图上量得甲,乙两地的距离是
5
cm,则甲,乙两地的实际距离是( ).
A.3
000
m
B.3
500
m
C.5
000
m
D.7
500
m
D
四、课堂训练
3.如图所示的两个四边形是否相似?
答案:不相似.
四、课堂训练
4.观察下面的图形(a)~(g),其中哪些是与图形(1),(2)或(3)相似的?
四、课堂训练
5.填空:
(1)如图
①
是两个相似的四边形,则
x=_______,y=_______
,α=_______.
(2)如图
②
是两个相似的矩形,
x=_______.
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图
①
3
5
30
20
15
x
2.5
1.5
90°
22.5
图
②
四、课堂训练
6.如图,把矩形
ABCD
对折,折痕为
EF,若矩形
ABCD
与矩形
EABF
相似,AB=1.
(1)求
BC
长;
(2)求矩形
ABEF
与矩形
ABCD
的相似比.
A
B
C
D
E
F
四、课堂训练
解:(1)∵ E
是
AD
的中点,
又∵ 矩形
ABCD
与矩形
EABF相似,AB=1,
四、课堂训练
解得
(2)矩形
ABEF
与矩形
ABCD
的相似比为:
五、作业
教科书习题
27.
1
第
2,3,5,6
题.
第二十七章 相似
27.1 图形的相似
第一课时
这一版邮票有什么特点?
一、情景导入
一、情景导入
形状,大小完全相同的图形是全等图形.
C′
A′
B′
C
A
B
圣诞老人的
2
寸照片和
4
寸照片,他的形状改变了吗?大小呢?
一、情景导入
一、情景导入
符合国家标准的两面共青团团旗的形状相同吗?大小呢?
二、探究新知
你能来归归类吗?
二、探究新知
下面的“猫咪”有什么相同和不同的地方?
二、探究新知
相同点:形状相同
不同点:大小不相同
归纳:
形状相同的图形叫做相似图形.
相似图形的大小不一定相同.
二、探究新知
图形的放大
二、探究新知
两个图形相似 图形的缩小
二、探究新知
相似图形的关系
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
二、探究新知
思考:你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
二、探究新知
放大镜下的图形和原来的图形相似吗?
放大镜下的角与原图形中角是什么关系?
三、课堂小结
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
四、课堂训练
1.下面的各组图形中,不相似的一组是( ).
A.
B.
C.
D.
D
四、课堂训练
2.下面每组图形中的两个图形,不是相似图形的是( ).
A.
B.
C.
D.
D
3.观察下面每组的每个图形,相似图形是( ).
A.
B.
C.
D.
四、课堂训练
A
四、课堂训练
4.下列说法不一定正确的是( ).
A.所有的矩形都相似
B.有一个角是
100°的两个等腰三角形相似
C.所有的圆都相似
D.所有的正方形都相似
A
四、课堂训练
5.如图,指出形状相同的图形.
解:(1)与(9);(2)与(11);
(3)与(6);(4)与(7);(5)与(12);
(8)与(10).
四、课堂训练
6.已知下列四种图形:
①
有一个角为直角的菱形;②
邻边相等的矩形;③
对角线相等且互相垂直的四边形;④
四边相等,四角也相等的四边形.剔除其中的一种图形,其余的三种图形形状相同,则剔除的应该是( ).
A.①
B.②
C.③
D.④
C
四、课堂训练
7.下列四组图形中,两个图形相似的有( ).
A.1
组
B.2
组
C.3
组
D.4
组
D
五、作业
教科书习题
27.
1
第
1,4
题.
第二十七章 相似
27.1 图形的相似
第二课时
一、情景导入
多边形
ABCDEF
是显示在电脑屏幕上的,而多边形
A1B1C1D1E1F1
是投射到银幕上的.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
一、情景导入
问题
1 这两个多边形相似吗?
问题
2 在这两个多边形中,是否有对应相等的内角?
问题
3 在这两个多边形中,夹相等内角的两边否成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
二、探究新知
对应角有什么关系?对应边有什么关系?
∠A=∠A1,∠B=∠B1,∠C=∠C1 对应角相等
AB=BC=AC,A1B1=B1C1=A1C1,
AB∶A1B1=BC∶B1C1
=CD∶C1D1,对应边成比例
A
B
C
正三角形
缩小
60°
A
B
C
60°
二、探究新知
对应角有什么关系?
正八边形
∠A=∠A1,∠A=∠A1,∠C=∠C1
,
∠D=∠D1,∠E=∠E1,∠F=∠F1
,对应角相等
150°
A
B
C
F
E
D
放大
150°
A1
B1
C1
F1
E1
D1
二、探究新知
对应边有什么关系?
正八边形
AB=BC=CD=DE=EF=FA,
A1B1=B1C1=C1D1=D1E1=E1F1=F1A1,
AB∶A1B1=BC∶B1C1=CD∶C1D1=DE∶D1E1=EF∶E1F1,
对应边成比例
150°
A
B
C
F
E
D
放大
150°
A1
B1
C1
F1
E1
D1
二、探究新知
相似多边形
对应角相等,对应边成比例.
相似比
相似多边形对应边的比.(k>0)
若相似比
k=1,相似图形有什么关系?
二、探究新知
当相似比
k=1
时,相似图形即是全等图形.
全等是一种特殊的相似.
二、探究新知
各对应角相等,各对应边成比例的多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
二、探究新知
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正
n
边形呢?
分析:已知等边三角形的每个角都为
60°,三边都相等.所以满足边数相等,对应角相等,以及对应边的比相等.
a1
a2
a3
an
……
二、探究新知
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
……
a1
a2
a3
an
二、探究新知
思考:任意的两个菱形(或矩形)是否相似?为什么?
二、探究新知
两个多边形相似的条件:
对应角相等,对应边成比例.
二、探究新知
例
1 如图,四边形
ABCD
和
EFGH
相似,求角
α,β
的大小和
EH
的长度
x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
二、探究新知
解:因为四边形
ABCD
和
EFGH
相似,所以它们的对应角相等,由此可得
α=∠C=83°,∠A=∠E=118°.
在四边形
ABCD
中,
β=360°-(78°+83°+118°)=81
°.
二、探究新知
因为四边形
ABCD
和
EFGH
相似,所以它们的对应边成比例,由此可得
解得
x=28
cm.
二、探究新知
例
2 如图所示的两个五边形相似,求未知边
a,b,c,d
的长度.
5
3
2
c
d
7.5
b
a
6
9
二、探究新知
解:相似多边形的对应边的比相等,由此可得
解得:
a=3,b=4.5,c=4,d=6.
所以未知边
a,b,c,d
的长度分别为
3,4.5,4,6.
三、课堂小结
相似多边形对应边的比叫做相似比.
对应角相等,对应边成比例.
相似多边形
ABDF
四、课堂训练
1.下列图形中能够确定相似的是(
).
A.两个半径不相等的圆
B.所有的等边三角形
C.所有的等腰三角形
D.所有的正方形
E.所有的等腰梯形
F.所有的正六边形
四、课堂训练
2.若一张地图的比例尺是
1∶150
000,在地图上量得甲,乙两地的距离是
5
cm,则甲,乙两地的实际距离是( ).
A.3
000
m
B.3
500
m
C.5
000
m
D.7
500
m
D
四、课堂训练
3.如图所示的两个四边形是否相似?
答案:不相似.
四、课堂训练
4.观察下面的图形(a)~(g),其中哪些是与图形(1),(2)或(3)相似的?
四、课堂训练
5.填空:
(1)如图
①
是两个相似的四边形,则
x=_______,y=_______
,α=_______.
(2)如图
②
是两个相似的矩形,
x=_______.
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图
①
3
5
30
20
15
x
2.5
1.5
90°
22.5
图
②
四、课堂训练
6.如图,把矩形
ABCD
对折,折痕为
EF,若矩形
ABCD
与矩形
EABF
相似,AB=1.
(1)求
BC
长;
(2)求矩形
ABEF
与矩形
ABCD
的相似比.
A
B
C
D
E
F
四、课堂训练
解:(1)∵ E
是
AD
的中点,
又∵ 矩形
ABCD
与矩形
EABF相似,AB=1,
四、课堂训练
解得
(2)矩形
ABEF
与矩形
ABCD
的相似比为:
五、作业
教科书习题
27.
1
第
2,3,5,6
题.
