27. 2.1 相似三角形的判定 课件(共5课时 117张)
文档属性
| 名称 | 27. 2.1 相似三角形的判定 课件(共5课时 117张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 10:33:53 | ||
图片预览





文档简介
(共117张PPT)
第二十七章 相似
27.
2.1 相似三角形的判定
第一课时 平行线分线段成比例
一、情景导入
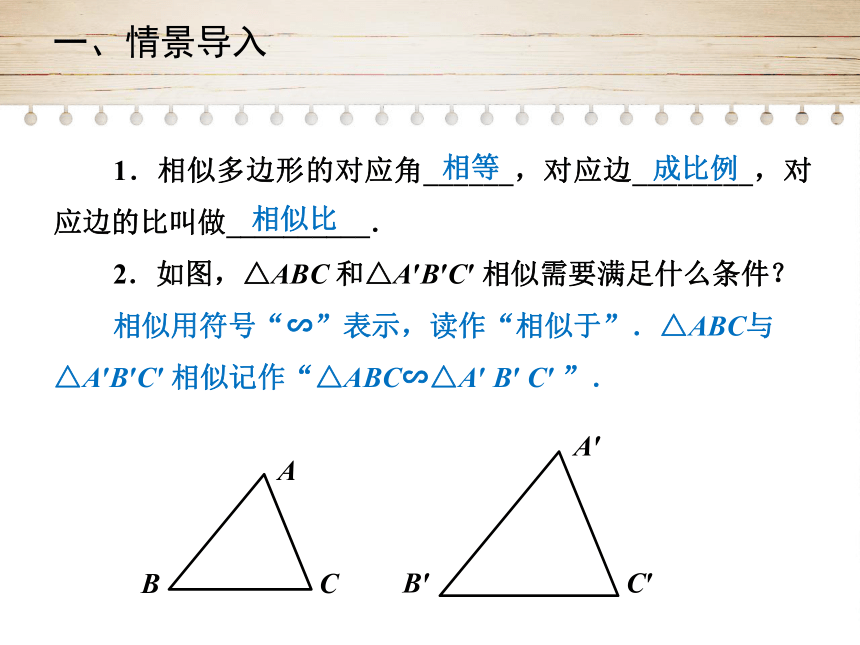
1.相似多边形的对应角______,对应边________,对应边的比叫做__________.
2.如图,△ABC
和△A′B′C′
相似需要满足什么条件?
相似用符号“∽”表示,读作“相似于”.△ABC与
△A′B′C′
相似记作“△ABC∽△A′
B′
C′
”.
A
B
C
A′
B′
C′
相等
成比例
相似比
二、探究新知
1.平行线分线段成比例(基本事实)
如图
①,小方格的边长都是
1,直线
a∥b∥c,分别交直线
m,n
于
A1,A2,A3,B1,B2,B3.
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
①
二、探究新知
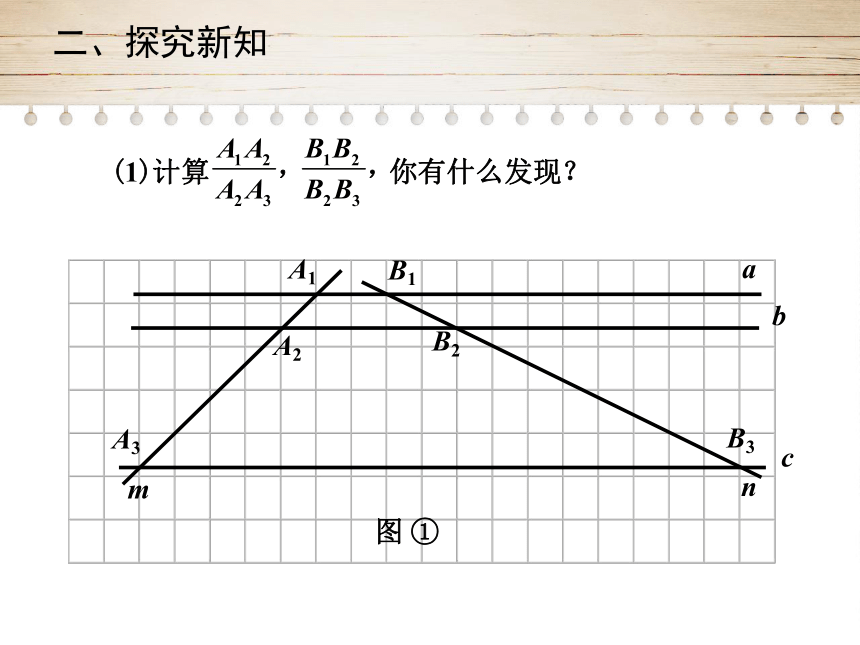
(1)计算
你有什么发现?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
①
二、探究新知
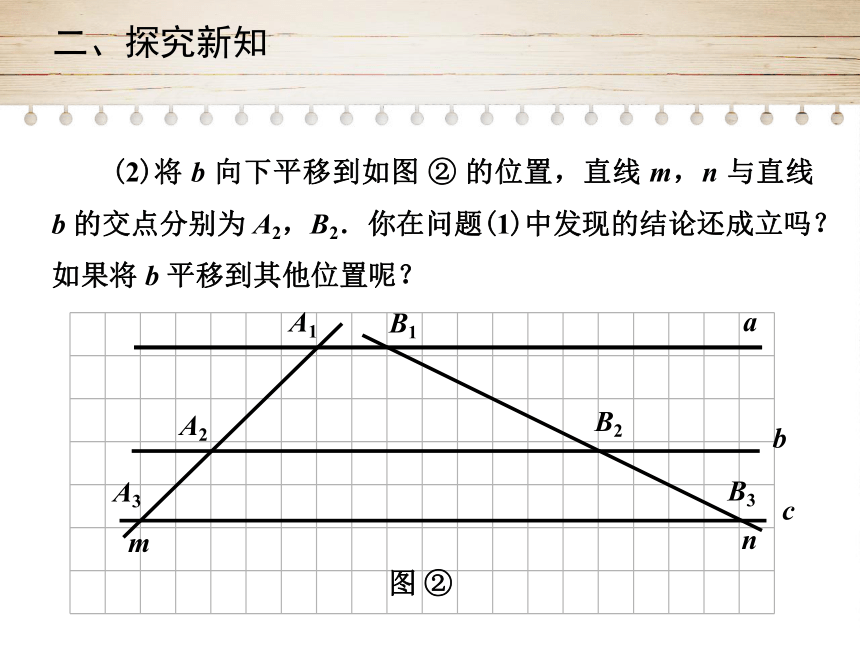
(2)将
b
向下平移到如图
②
的位置,直线
m,n
与直线
b
的交点分别为
A2,B2.你在问题(1)中发现的结论还成立吗?如果将
b
平移到其他位置呢?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
②
二、探究新知
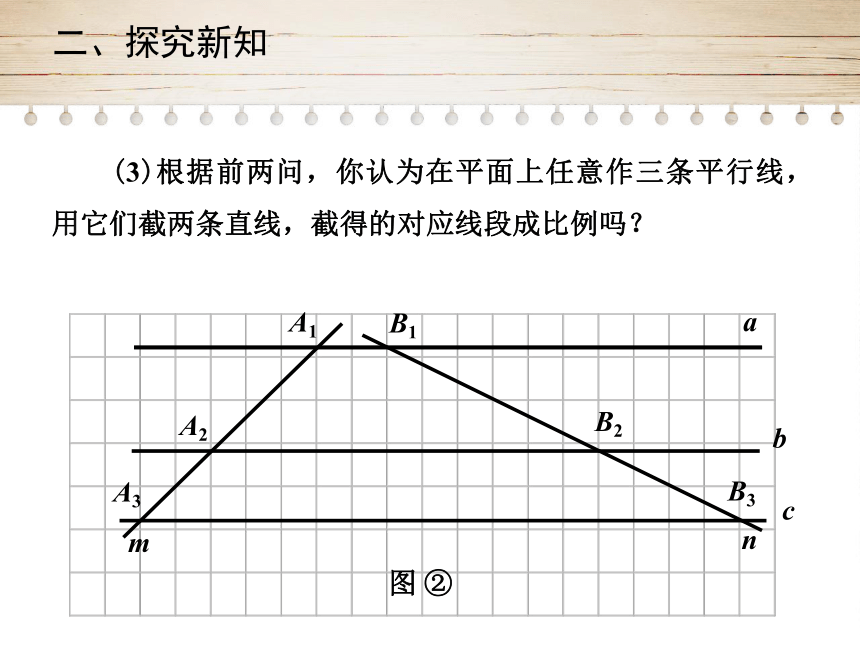
(3)根据前两问,你认为在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
②
二、探究新知
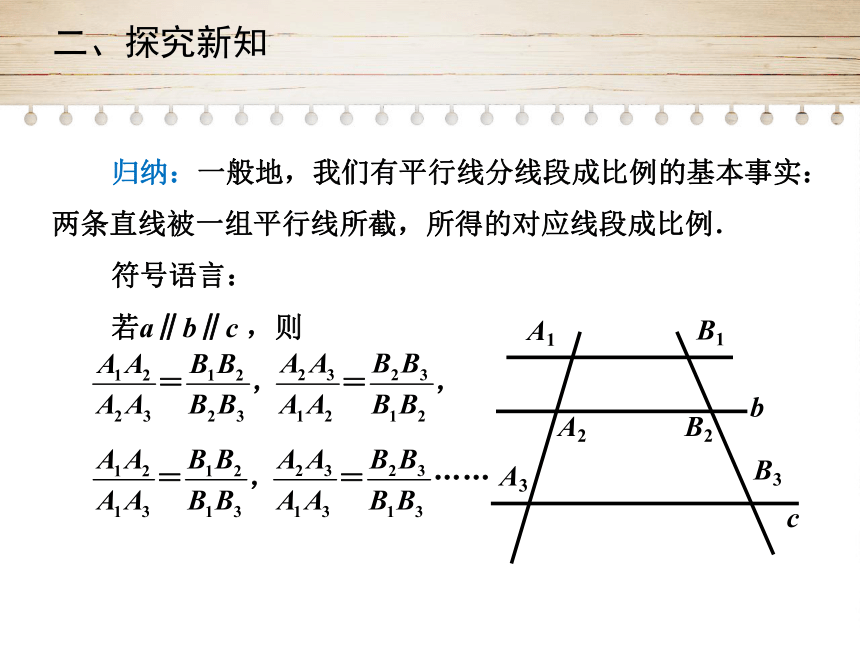
归纳:一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥c
,则
A1
A2
A3
B1
B2
B3
b
c
二、探究新知
想一想:
1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
二、探究新知
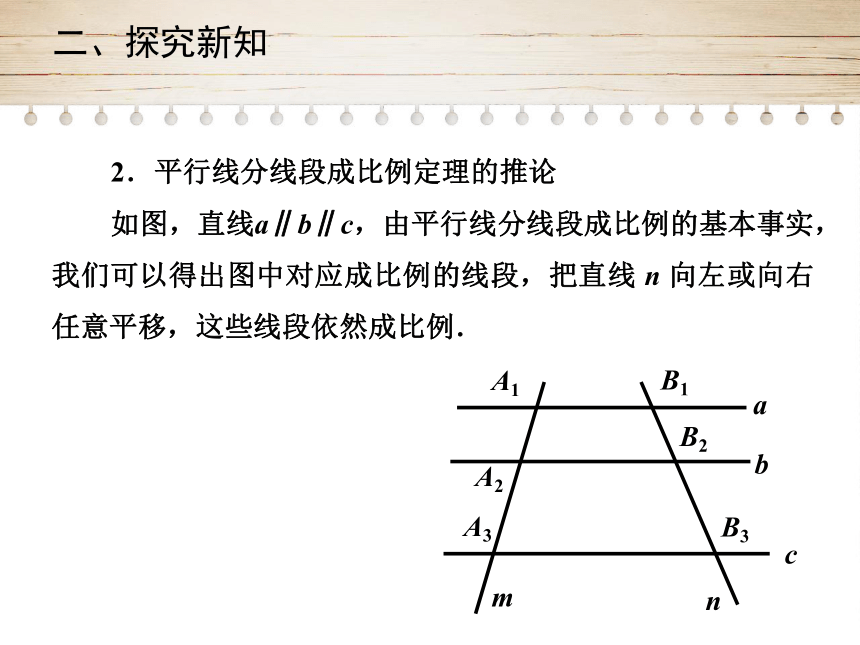
2.平行线分线段成比例定理的推论
如图,直线a∥b∥c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,把直线
n
向左或向右任意平移,这些线段依然成比例.
A1
A2
A3
B1
B2
B3
b
c
m
n
a
二、探究新知
直线
n
向左平移到
B1
与A1
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1
A2
A3
b
c
m
B1
B2
B3
n
a
A1(B1)
A2
A3
B2
B3
(B1)
二、探究新知
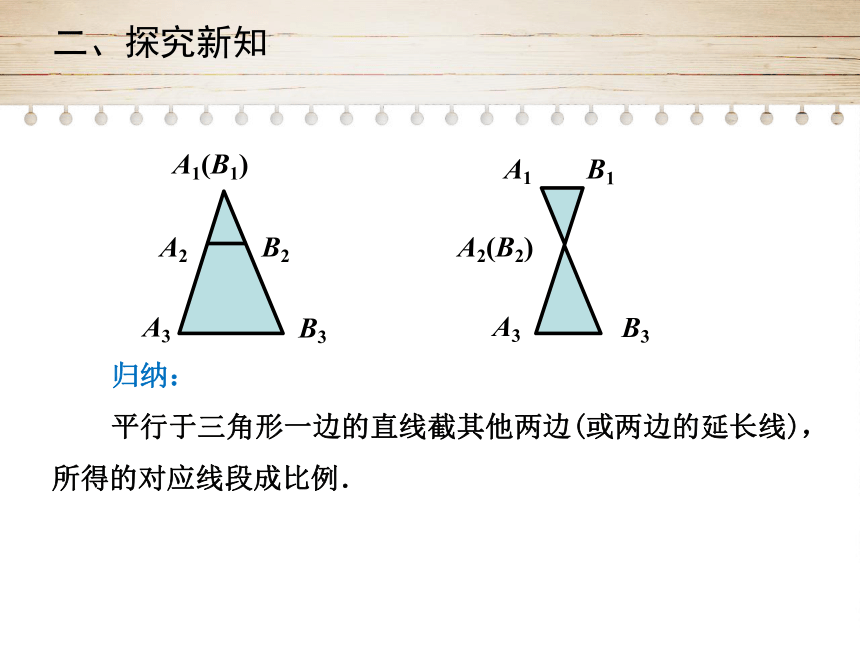
归纳:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
二、探究新知
例
1 如图,在△ABC
中,
EF∥BC.
(1)如果
E、F
分别是
AB
和
AC
上的点,AE=BE=7,
FC=4,那么
AF
的长是多少?
(2)如果
AB=10,AE=6,AF=5,那么
FC
的长是多
少?
A
B
C
E
F
二、探究新知
解:(1)
∵
∴
解得
AF=4.
二、探究新知
(2)∵
∴
解得
AC=
∴ FC=AC-AF=
二、探究新知
3.相似三角形的引理
如图,在△ABC
中,D
为
AB
上任意一点,过点
D
作BC
的平行线
DE
,交
AC
于点
E.
问题
1 △ADE
与△ABC
的三个角分别相等吗?
问题
2 分别度量△ADE
与△ABC
的边长,它们的边长是否对应成比例?
B
C
A
D
E
二、探究新知
问题
3 你认为△ADE
与△ABC
之间有什么关系?平行移动
DE
的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,且只要
DE∥BC,这个结论恒成立.
B
C
A
D
E
二、探究新知
想一想:我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
由前面的结论,我们可以得到什么?还需证明什么?
B
C
A
D
E
二、探究新知
由前面的结论可得
需要证明的是
而除
DE
外,其他的线段都在△ABC
的边上,要想利用前面学到的结论来证明三角形相似,需要怎样做呢?
可以将
DE
平移到
BC
边上去.
B
C
A
D
E
二、探究新知
用相似的定义证明△ADE∽△ABC.
证明:在
△ADE
与
△ABC
中∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点
D
作
DF∥AC,交
BC
于点
F.
∵ DE∥BC,DF∥AC,
C
A
B
D
E
F
二、探究新知
∴
∵ 四边形
DFCE
为平行四边形,
∴ DE=FC,
∴
∴ △ADE∽△ABC.
二、探究新知
由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
二、探究新知
三角形相似的两种常见类型:
“A”型
“X”型
D
E
A
B
C
A
B
C
D
E
三、课堂小结
推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理:平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例
四、课堂训练
1.如图,已知
l1∥l2∥l3,下列比例式中错误的是( ).
A.
B.
C.
D.
A
C
E
B
D
F
l2
l1
l3
D
四、课堂训练
2.如图,DE∥BC,
则
_______
;FG∥BC,
则
_______
.
A
B
C
E
D
F
G
四、课堂训练
3.已知:如图,AB∥EF∥CD,图中共有_______
对相似三角形.
C
D
A
B
E
F
O
3
四、课堂训练
4.若△ABC
与△A′B′C′
相似,一组对应边的长为
AB=3
cm,A′B′=4
cm,那么△A′B′C′
与△ABC
的相似比是_____.
4︰3
四、课堂训练
5.如图,在△ABC
中,DE∥BC,则△
____
∽△
____,对应边的比例式为
=
____
=
____
.
B
C
A
D
E
ADE
ABC
四、课堂训练
6.已知△ABC∽△A1B1C1,相似比是
1∶4,△A1B1C1∽△A2B2C2,相似比是
1∶5,则△ABC
与△A2B2C2
的相似比为_______.
1∶20
四、课堂训练
7.如图,在□ABCD
中,EF∥AB,DE∶EA=2∶3,EF=4,求
CD
的长.
解:∵ EF∥AB,DE∶EA=2∶3,
∴ △DEF
∽
△DAB.
∴
即
解得
AB=10.
又
∵ 四边形
ABCD
为□,
∴ CD=AB=10.
D
A
C
B
E
F
四、课堂训练
8.如图,已知菱形
ABCD
内接于△AEF,AE=5
cm,AF=4
cm,求菱形的边长.
解:∵ 四边形
ABCD
为菱形,
∴ CD∥AB,
∴
设菱形的边长为
x
cm,则
CD=AD=x
cm,DF=(4-x)cm,
∴
解得
x=
∴菱形的边长为
cm.
五、作业
教科书第
42
页习题
27.
2
第
4,5
题.
第二十七章 相似
27.
2.1 相似三角形的判定
第二课时 三边成比例的两个三角形相似
一、情景导入
1.什么是相似三角形?在前面的课程中,我们学过哪些判定三角形相似的方法?
2.证明三角形全等有哪些方法?
3.类似于判定三角形全等的
SSS
方法,我们能不能通过三边来判定两个三角形相似呢?
A
B
C
D
E
一、情景导入
画
△ABC
和
△A′B′C′,使
动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
二、探究新知
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以△ABC
∽△A′B′C′.下面我们用前面所学得定理证明该结论.
A
B
C
C′
B′
A′
二、探究新知
证明:
在线段
AB(或延长线)上截取
AD=A′B′,
过点
D
作
DE∥BC
交
AC
于点
E.
∵ DE∥BC
,
∴ △ADE∽△ABC.
∴
又
AD=A′B′,
∴
C′
B′
A′
B
C
A
D
E
二、探究新知
∴ DE=B′C′,EA=C′A′.
∴ △ADE≌△A′B′C′,△A′B′C′
∽△ABC.
二、探究新知
归纳:
由此我们得到利用三边判定三角形相似的定理:三边成比例的两个三角形相似.
符号语言:
∵
∴
△
ABC
∽
△A′B′C′.
二、探究新知
例
1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
二、探究新知
解:在△ABC
中,AB>BC>CA,在△DEF
中,
DE>
EF>FD.
∵
∴
∴ △ABC
∽
△DEF.
二、探究新知
方法总结:判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等.
注意:计算时最长边与最长边对应,最短边与最短边对应.
二、探究新知
例
2 如图,在
Rt△ABC
与
Rt△A′B′C′
中,∠C=∠C′
=90?,且
求证:△
A′B′C′∽△ABC.
二、探究新知
证明:由已知条件得
AB=2A′B′,AC=2A′C′,
∴ BC2=AB2-AC2=(2A′B′)2-(2A′C′)2=4A′B′2-4A′C′2=4(A′B′2-A′C′2)=4B′C′2=(2B′C′)2.
∴ BC=2B′C′,
∴ △A′B′C′∽△ABC.(三边对应成比例的两个三角形相似)
二、探究新知
例
3 如图,在
△ABC
和
△ADE
中,
∠BAD=20°,求∠CAE
的度数.
A
B
C
D
E
二、探究新知
解:∵
∴ △ABC
∽△ADE.
∴ ∠BAC=∠DAE,∠BAC-∠DAC=∠DAE-∠DAC,
即 ∠BAD=∠CAE.
∵ ∠BAD=20°,
∴ ∠CAE=20°.
二、探究新知
例
4 如图,已知
AB∶AD=BC∶DE=AC∶AE,找出图中相等的角(对顶角除外),并说明你的理由.
A
B
C
D
E
二、探究新知
解:在
△ABC
和
△ADE
中,
∵ AB∶CD=BC∶DE=AC∶AE,
∴ △ABC∽△ADE.
∴ ∠BAC=∠DAE,∠B=∠D,∠C=∠E.
∴ ∠BAC-∠CAD
=∠DAE-∠CAD
.
∴ ∠BAD=∠CAE.
故图中相等的角有∠BAC=∠DAE,∠B=∠D,∠C=∠E,∠BAD=∠CAE.
三、课堂小结
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.已知
△ABC
和
△DEF,根据下列条件判断它们是否相似.
(1)AB=3,BC=4,AC=6,
DE=6,EF=8,DF=9;
(2)AB=4,BC=8,AC=10,
DE=20,EF=16,DF=8;
(3)AB=12,BC=15,AC=24,
DE=16,EF=20,DF=30.
是
否
否
四、课堂训练
2.如图,在大小为
4×4
的正方形网格中,是相似三角形的是( ).
A.
①
和
②
B.②
和
③
C.
①
和
③
D.②
和
④
①
②
③
④
C
四、课堂训练
3.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是( ).
A.△PAB∽△PCA
B.△PAB∽△PDA
C.△ABC∽△DBA
D.△ABC∽△DCA
A
C
B
P
D
C
四、课堂训练
解析:设AP=PB=BC=CD=1,
∵ ∠APD=90°,
∴ AB=
AC=
AD=
∵
AB∶BC=BD∶AB=AD∶AC,
∴ △ABC∽△DBA,故选
C.
四、课堂训练
4.根据下列条件,判断△ABC
与△A′B′C′
是否相似:
AB=4
cm,BC=6
cm,AC=8
cm,A′B′=12
cm,B′C′=18
cm,A′C′=21
cm.
答案:不相似.
四、课堂训练
5.如图,△ABC
中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
四、课堂训练
证明:∵△ABC
中,点
D,E,F
分别是
AB,BC,CA的中点,
∴
∴
∴ △ABC∽△EFD.
四、课堂训练
6.如图,某地四个乡镇
A,B,C,D
之间建有公路,已知
AB=14
千米,AD=28
千米,BD=21
千米,DC=31.5
千米,公路
AB
与
CD
平行吗?说出你的理由.
A
C
B
D
28
14
21
42
31.5
四、课堂训练
解:公路
AB
与
CD
平行.
∴
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC,
∴ AB∥DC.
五、作业
教科书第
34
页练习第
2,3
题.
教科书第
42
页习题
27.2
第
1,2
题.
第二十七章 相似
27.2.1 相似三角形的判定
第三课时 两边成比例且夹角相等的
两个三角形相似
一、情景导入
1.回忆我们学习过的判定三角形相似的方法.类比证明三角形全等的方法,猜想证明三角形相似还有哪些方法?
2.类似于判定三角形全等的
SAS
方法,能不能通过两边和夹角来判定两个三角形相似呢?
二、探究新知
用刻度尺和量角器画
△ABC
和
△A′B′C′,使∠A=∠A′,
量出
BC
及
B′C′
的长,它们的比值等于
k
吗?再量一量两个三角形另外的两个角,你有什么发现?△ABC
与
△A′B′C′
有何关系?
改变
k
和∠A
的值的大小,是否有同样的结论?
二、探究新知
如图,在
△ABC
与
△A′B′C′
中,已知
∠A=∠A′,求证:△ABC∽△A′B′C′.
证明:在
△A′B′C′
的边
A′B′
上
截取点
D,使
A′D=AB.过点
D
作
DE∥B′C′,交
A′C′
于点
E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
∴
B
A
C
D
E
B'
A'
C'
二、探究新知
∵ A′D=AB,
∴
∴ A′E=AC.
又 ∠A′=∠A.
∴ △A′DE
≌
△ABC,
∴ △A′B′C′
∽
△ABC.
二、探究新知
归纳:
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
∴ △ABC
∽
△A′B′C′.
B
A
C
B'
A'
C'
二、探究新知
思考:对于
△ABC
和
△A′B′C′,如果
A′B′∶AB=A′C′∶AC.∠B=∠B′,这两个三角形一定会相似吗?
不会,如下图,因为不能证明构造的三角形和原三角形全等.
A
B
C
A′
B′
B″
C′
二、探究新知
结论:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
二、探究新知
例
1 根据下列条件,判断△ABC
和△A′B′C′
是否相似,并说明理由:
∠A=120°
,AB=7
cm,AC=14
cm,
∠A′=120°,A′B′=3
cm
,A′C′=6
cm.
解:∵
∴
又 ∠A′=∠A,
∴ △ABC
∽
△A′B′C′.
二、探究新知
例
2 如图,△ABC
与△ADE
都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC
∽△ADE.
证明:∵ △ABC
与
△ADE
是等腰三角形,
∴ AD=AE,AB=AC,
∴
又∵ ∠DAB=∠CAE,
∴ ∠DAB
+∠BAE=∠CAE
+∠BAE,
即 ∠DAE=∠BAC,
∴ △ABC
∽
△ADE.
A
B
C
D
E
二、探究新知
例
3 如图,D,E
分别是△ABC
的边
AC,AB
上的点,AE=1.5,AC=2,BC=3,且
求
DE
的长.
A
C
B
E
D
二、探究新知
解:∵ AE=1.5,AC=2,
∴
又∵ ∠EAD=∠CAB,
∴
△ADE
∽△ABC,
∴
∴
二、探究新知
例
4 如图,
在△ABC
中,CD
是边
AB
上的高,且
求证
∠ACB=90°.
A
B
C
D
二、探究新知
证明:
∵ CD
是边
AB
上的高,
∴ ∠ADC=∠CDB=90°.
∵
∴ △ADC
∽△CDB.
∴ ∠ACD=∠B,
∴ ∠ACB=∠ACD+∠BCD=∠B+∠BCD=90°.
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
三、课堂小结
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.判断.
(1)两个等边三角形相似.
( )
(2)两个直角三角形相似.
( )
(3)两个等腰直角三角形相似.
( )
(4)有一个角是
50°的两个等腰三角形相似.
( )
×
√
√
×
四、课堂训练
2.如图,D
是△ABC
一边
BC
上一点,连接
AD,使
△ABC
∽
△DBA
的条件是( ).
A.AC∶BC=AD∶BD
B.AC∶BC=AB∶
AD
C.AB2=CD
·
BC
D.AB2=BD
·
BC
A
B
C
D
D
四、课堂训练
3.如图△AEB
和△FEC_______
(填“相似”或“不相似”).
54
30
36
45
E
A
F
C
B
相似
四、课堂训练
4.如图,已知△ABC
中,D
为边
AC
上一点,P
为边
AB
上一点,AB=12,AC=8,AD=6,当
AP
的长度为
_______
时,△ADP
和△ABC
相似.
A
B
C
D
4
或
9
四、课堂训练
解:当△ADP
∽△ACB
时,
AP∶AB=AD∶AC
,
∴ AP∶12=6∶8.
解得
AP=9;
当△ADP
∽△ABC
时,
AD∶AB=AP∶AC,
∴ 6∶12=AP∶8,
解得
AP=4.
∴ 当
AP
的长度为
4
或
9
时,△ADP
和△ABC
相似.
A
B
C
D
P
P
四、课堂训练
5.如图,在四边形
ABCD
中,已知
∠B=∠ACD,
AB=6,BC=4,AC=5,CD=
,求
AD
的长.
A
B
C
D
四、课堂训练
解:∵ AB=6,BC=4,AC=5,CD=
,
∴
又∵ ∠B=∠ACD,
∴ △ABC
∽
△DCA,
∴
∴
四、课堂训练
6.如图,∠DAB=∠CAE,且
AB·AD=AE·AC,求证
△ABC
∽△AED.
证明:∵ AB
·
AD=AE
·
AC,
∴
又∵ ∠DAB=∠CAE,
∴ ∠
DAB+∠BAE=∠CAE+∠BAE,
即 ∠DAE=∠BAC,
∴
△ABC
∽△AED.
A
B
C
D
E
五、作业
教科书第
42
页习题
27.
2
第
3
题.
第二十七章 相似
27.2.1 相似三角形的判定
第四课时 两角分别相等的两个三角形相似
一、情景导入
学校举办活动,需要三个内角分别为
90°,60°,30°的形状相同,大小不同的三角纸板若干.小明手上的测量工具只有一个量角器,他该怎么做呢?
?
?
?
二、探究新知
与同伴合作,一人画△ABC,另一人画△A′B′C′,使∠A=∠A′,∠B=∠B′,探究下列问题:
问题一 度量
AB,BC,AC,A′B′,B′C′,A′C′
的长,并计算出它们的比值.你有什么发现?
C
A
B
A'
B'
C'
二、探究新知
问题二 试证明△A′B′C′∽△ABC.
证明:在△ABC
的边
AB(或
AB
的延长线)上,截取
AD=A′B′,过点
D
作
DE∥BC,交
AC
于点
E,则有△ADE
∽△ABC,∠ADE=∠B.
∵ ∠B=∠B′,
∴ ∠ADE=∠B′.
又∵
AD=A′B′,∠A=∠A′,
∴ △ADE
≌△A′B′C′.
∴ △A′B′C′
∽△ABC.
C
A
A'
B
B'
C'
D
E
二、探究新知
归纳:
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC∽△A'B'C'.
C
A
B
A'
B'
C'
二、探究新知
例
1 如图,△ABC
和△DEF
中,∠A=40°,∠B=80°,∠E=80°,∠F=60°.求证:△ABC
∽△DEF.
证明:∵ 在
△ABC
中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A-∠B=60°.
∵ 在
△DEF
中,
∠E=80°,
∠F=60°.
∴ ∠B=∠E
,
∠C=∠F.
∴ △ABC
∽△DEF.
A
C
B
F
E
D
二、探究新知
例
2 如图,弦
AB
和
CD
相交于
⊙O
内一点
P,求证:PA·PB=PC·PD.
证明:连接
AC,DB.
∵ ∠A
和
∠D
都是弧
CB
所对的圆周角,
∴ ∠A=
_______.
同理 ∠C=
_______,
∴ △PAC
∽
△PDB.
∴ __________
即
PA·PB=PC·PD.
∠D
∠B
O
D
C
B
A
P
三、课堂小结
两角分别相等的两个三角形相似
利用两角判定三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.如图,在△ABC
和△A'B'C'中,若∠A=60°,∠B=40°,∠A'=60°,当∠C'=_____时,△ABC
∽△A'B'C'.
80°
C
A
B
B'
C'
A'
四、课堂训练
2.如图,△ABC
中,AE
交
BC
于点
D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则
DC
的长等于( ).
A.
B.
C.
D.
A
C
A
B
D
E
四、课堂训练
3.如图,点
D
在
AB
上,当∠_______
=∠_______
(或∠_______
=∠_______
)时,
△ACD∽△ABC.
ACD
B
ACB
ADB
A
B
D
C
四、课堂训练
4.如图,⊙O
的弦
AB,CD
相交于点
P,若
PA=3,
PB=8,PC=4,则
PD=____.
6
O
D
C
B
A
P
四、课堂训练
5.如图,△ABC
中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
证明:∵ DE∥BC,
EF∥AB,
∴ ∠AED=∠C,
∵ ∠A=∠FEC.
∴ △ADE∽△EFC.
A
E
F
B
C
D
五、作业
教科书第
36
页练习第
1
题.
教科书第
57
页复习题
27
第
1,2,3题.
第二十七章 形似
27.2.1 相似三角形的判定
第五课时 直角三角形相似的判定
一、情景导入
1.
回忆我们学习过的判定三角形相似的方法.
2.类似于判定三角形全等的方法,能不能通过直角边与斜边来判定两个三角形相似呢?
二、探究新知
利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A'
,∠B=∠B',
∴ △ABC
∽
△A'B'C'.
C
A
B
A'
B'
C'
二、探究新知
归纳:由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
二、探究新知
思考:对于两个直角三角形,我们还可以用
“HL”判定它们全等.那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
二、探究新知
证明:设______________=k,则
AB=kA′B′,AC=kA′B′.由__________
,得
∴
∴ Rt
△ABC
∽
Rt
△A′B′C′.
C
A
A'
B
B'
C'
勾股定理
二、探究新知
归纳:由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
二、探究新知
例
1 如图,在
Rt△ABC
中,∠C=90°,AB=10,AC=8.E
是
AC
上一点,AE=5,ED⊥AB,垂足为
D.
求AD
的长.
解:∵ ED⊥AB,
∴ ∠EDA=90°.
又 ∠C=90°,∠A=∠A,
D
A
B
C
E
二、探究新知
∴ △AED
∽△ABC.
∴
∴
二、探究新知
例
2 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
,当
AB
的长为____________时,△ACB
与
△ADC相似.
C
A
B
D
二、探究新知
解析:∵ ∠ADC=90°,AD=2,CD=
,
∴
要使这两个直角三角形相似,有两种情况:
(1)当
Rt△ABC
∽
Rt△ACD
时,有
AC
:
AD=AB∶AC,即
∶2=AB∶
,解得
AB=3;
(2)当
Rt△ACB
∽
Rt△CDA
时,有
AC
:
CD=AB∶AC,
即
∶
=AB∶
,解得
AB=
∴ 当
AB
的长为
3
或
时,这两个直角三角形相似.
三、课堂小结
两角分别相等的两个三角形相似
相似三角形的判定定理的运用
直角三角形相似的判定
四、课堂训练
1.在
Rt△ABC
和
Rt△A′B′C′
中,∠C=∠C′=90°
,依据下列各组条件判定这两个三角形是否相似.
(1)∠A=35°
,∠B′=55°:_______
;
(2)AC=3,BC=4,A′C′=6,B′C′=8:_______
;
(3)AB=10,AC=8,A′B′=25,B′C′=15:_______
.
相似
相似
相似
四、课堂训练
2.如图,已知
AB∥DE,∠AFC=∠E,则图中相似三角形共有( ).
A.1对
B.2对
C.3对
D.4对
C
四、课堂训练
3.如图,在
Rt△ABC
中,∠ABC=90°,BD⊥AC于D.若
AB=6,AD=2,则
AC=_______
,BD=_______
,BC=_______
.
D
B
C
A
18
四、课堂训练
4.如图,△ABC
的高
AD,BE
交于点
F.
求证:
D
C
A
B
E
F
四、课堂训练
证明:
∵ △ABC
的高
AD,BE
交于点
F,
∴ ∠FEA=∠FDB=90°,
∠AFE=∠BFD(对顶角相等).
∴ △FEA
∽
△
FDB,
∴
四、课堂训练
5.如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
证明:∵ ∠BAC=∠1+∠DAC,
∠DAE=∠3+∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=∠E.
∴
△ABC∽△ADE.
A
B
C
D
E
1
3
2
O
四、课堂训练
6.如图,BE
是
△ABC
的外接圆
O
的直径,CD
是△ABC
的高,
求证:AC·BC=BE·CD.
证明:
连接
CE,则∠A=∠E.
又∵ BE
是
△ABC
的外接圆
O
的直径,
∴ ∠BCE=90?=∠ADC.
∵ ∠A=∠E,∠BCE=∠ADC,
∴ △ACD∽△EBC.
∴
∴
AC·BC=BE·CD.
O
D
C
B
A
E
五、作业
教科书第
36
页练习第
2,3
题.
第二十七章 相似
27.
2.1 相似三角形的判定
第一课时 平行线分线段成比例
一、情景导入
1.相似多边形的对应角______,对应边________,对应边的比叫做__________.
2.如图,△ABC
和△A′B′C′
相似需要满足什么条件?
相似用符号“∽”表示,读作“相似于”.△ABC与
△A′B′C′
相似记作“△ABC∽△A′
B′
C′
”.
A
B
C
A′
B′
C′
相等
成比例
相似比
二、探究新知
1.平行线分线段成比例(基本事实)
如图
①,小方格的边长都是
1,直线
a∥b∥c,分别交直线
m,n
于
A1,A2,A3,B1,B2,B3.
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
①
二、探究新知
(1)计算
你有什么发现?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
①
二、探究新知
(2)将
b
向下平移到如图
②
的位置,直线
m,n
与直线
b
的交点分别为
A2,B2.你在问题(1)中发现的结论还成立吗?如果将
b
平移到其他位置呢?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
②
二、探究新知
(3)根据前两问,你认为在平面上任意作三条平行线,用它们截两条直线,截得的对应线段成比例吗?
A1
A2
A3
B1
B2
B3
m
n
a
b
c
图
②
二、探究新知
归纳:一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:
若a∥b∥c
,则
A1
A2
A3
B1
B2
B3
b
c
二、探究新知
想一想:
1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?
二、探究新知
2.平行线分线段成比例定理的推论
如图,直线a∥b∥c,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,把直线
n
向左或向右任意平移,这些线段依然成比例.
A1
A2
A3
B1
B2
B3
b
c
m
n
a
二、探究新知
直线
n
向左平移到
B1
与A1
重合的位置,说说图中有哪些成比例线段?
把图中的部分线擦去,得到新的图形,刚刚所说的线段是否仍然成比例?
A1
A2
A3
b
c
m
B1
B2
B3
n
a
A1(B1)
A2
A3
B2
B3
(B1)
二、探究新知
归纳:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
A1(B1)
A2
A3
B2
B3
A2(B2)
A1
A3
B1
B3
二、探究新知
例
1 如图,在△ABC
中,
EF∥BC.
(1)如果
E、F
分别是
AB
和
AC
上的点,AE=BE=7,
FC=4,那么
AF
的长是多少?
(2)如果
AB=10,AE=6,AF=5,那么
FC
的长是多
少?
A
B
C
E
F
二、探究新知
解:(1)
∵
∴
解得
AF=4.
二、探究新知
(2)∵
∴
解得
AC=
∴ FC=AC-AF=
二、探究新知
3.相似三角形的引理
如图,在△ABC
中,D
为
AB
上任意一点,过点
D
作BC
的平行线
DE
,交
AC
于点
E.
问题
1 △ADE
与△ABC
的三个角分别相等吗?
问题
2 分别度量△ADE
与△ABC
的边长,它们的边长是否对应成比例?
B
C
A
D
E
二、探究新知
问题
3 你认为△ADE
与△ABC
之间有什么关系?平行移动
DE
的位置,你的结论还成立吗?
通过度量,我们发现△ADE∽△ABC,且只要
DE∥BC,这个结论恒成立.
B
C
A
D
E
二、探究新知
想一想:我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?
由前面的结论,我们可以得到什么?还需证明什么?
B
C
A
D
E
二、探究新知
由前面的结论可得
需要证明的是
而除
DE
外,其他的线段都在△ABC
的边上,要想利用前面学到的结论来证明三角形相似,需要怎样做呢?
可以将
DE
平移到
BC
边上去.
B
C
A
D
E
二、探究新知
用相似的定义证明△ADE∽△ABC.
证明:在
△ADE
与
△ABC
中∠A=∠A.
∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
如图,过点
D
作
DF∥AC,交
BC
于点
F.
∵ DE∥BC,DF∥AC,
C
A
B
D
E
F
二、探究新知
∴
∵ 四边形
DFCE
为平行四边形,
∴ DE=FC,
∴
∴ △ADE∽△ABC.
二、探究新知
由此我们得到判定三角形相似的定理:
平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
二、探究新知
三角形相似的两种常见类型:
“A”型
“X”型
D
E
A
B
C
A
B
C
D
E
三、课堂小结
推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
相似三角形判定的引理:平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例
四、课堂训练
1.如图,已知
l1∥l2∥l3,下列比例式中错误的是( ).
A.
B.
C.
D.
A
C
E
B
D
F
l2
l1
l3
D
四、课堂训练
2.如图,DE∥BC,
则
_______
;FG∥BC,
则
_______
.
A
B
C
E
D
F
G
四、课堂训练
3.已知:如图,AB∥EF∥CD,图中共有_______
对相似三角形.
C
D
A
B
E
F
O
3
四、课堂训练
4.若△ABC
与△A′B′C′
相似,一组对应边的长为
AB=3
cm,A′B′=4
cm,那么△A′B′C′
与△ABC
的相似比是_____.
4︰3
四、课堂训练
5.如图,在△ABC
中,DE∥BC,则△
____
∽△
____,对应边的比例式为
=
____
=
____
.
B
C
A
D
E
ADE
ABC
四、课堂训练
6.已知△ABC∽△A1B1C1,相似比是
1∶4,△A1B1C1∽△A2B2C2,相似比是
1∶5,则△ABC
与△A2B2C2
的相似比为_______.
1∶20
四、课堂训练
7.如图,在□ABCD
中,EF∥AB,DE∶EA=2∶3,EF=4,求
CD
的长.
解:∵ EF∥AB,DE∶EA=2∶3,
∴ △DEF
∽
△DAB.
∴
即
解得
AB=10.
又
∵ 四边形
ABCD
为□,
∴ CD=AB=10.
D
A
C
B
E
F
四、课堂训练
8.如图,已知菱形
ABCD
内接于△AEF,AE=5
cm,AF=4
cm,求菱形的边长.
解:∵ 四边形
ABCD
为菱形,
∴ CD∥AB,
∴
设菱形的边长为
x
cm,则
CD=AD=x
cm,DF=(4-x)cm,
∴
解得
x=
∴菱形的边长为
cm.
五、作业
教科书第
42
页习题
27.
2
第
4,5
题.
第二十七章 相似
27.
2.1 相似三角形的判定
第二课时 三边成比例的两个三角形相似
一、情景导入
1.什么是相似三角形?在前面的课程中,我们学过哪些判定三角形相似的方法?
2.证明三角形全等有哪些方法?
3.类似于判定三角形全等的
SSS
方法,我们能不能通过三边来判定两个三角形相似呢?
A
B
C
D
E
一、情景导入
画
△ABC
和
△A′B′C′,使
动手量一量这两个三角形的角,它们分别相等吗?这两个三角形是否相似?
A
B
C
C′
B′
A′
二、探究新知
通过测量不难发现∠A=∠A',∠B=∠B',∠C=∠C',又因为两个三角形的边对应成比例,所以△ABC
∽△A′B′C′.下面我们用前面所学得定理证明该结论.
A
B
C
C′
B′
A′
二、探究新知
证明:
在线段
AB(或延长线)上截取
AD=A′B′,
过点
D
作
DE∥BC
交
AC
于点
E.
∵ DE∥BC
,
∴ △ADE∽△ABC.
∴
又
AD=A′B′,
∴
C′
B′
A′
B
C
A
D
E
二、探究新知
∴ DE=B′C′,EA=C′A′.
∴ △ADE≌△A′B′C′,△A′B′C′
∽△ABC.
二、探究新知
归纳:
由此我们得到利用三边判定三角形相似的定理:三边成比例的两个三角形相似.
符号语言:
∵
∴
△
ABC
∽
△A′B′C′.
二、探究新知
例
1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
3
3.5
4
D
F
E
1.8
2.1
2.4
二、探究新知
解:在△ABC
中,AB>BC>CA,在△DEF
中,
DE>
EF>FD.
∵
∴
∴ △ABC
∽
△DEF.
二、探究新知
方法总结:判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等.
注意:计算时最长边与最长边对应,最短边与最短边对应.
二、探究新知
例
2 如图,在
Rt△ABC
与
Rt△A′B′C′
中,∠C=∠C′
=90?,且
求证:△
A′B′C′∽△ABC.
二、探究新知
证明:由已知条件得
AB=2A′B′,AC=2A′C′,
∴ BC2=AB2-AC2=(2A′B′)2-(2A′C′)2=4A′B′2-4A′C′2=4(A′B′2-A′C′2)=4B′C′2=(2B′C′)2.
∴ BC=2B′C′,
∴ △A′B′C′∽△ABC.(三边对应成比例的两个三角形相似)
二、探究新知
例
3 如图,在
△ABC
和
△ADE
中,
∠BAD=20°,求∠CAE
的度数.
A
B
C
D
E
二、探究新知
解:∵
∴ △ABC
∽△ADE.
∴ ∠BAC=∠DAE,∠BAC-∠DAC=∠DAE-∠DAC,
即 ∠BAD=∠CAE.
∵ ∠BAD=20°,
∴ ∠CAE=20°.
二、探究新知
例
4 如图,已知
AB∶AD=BC∶DE=AC∶AE,找出图中相等的角(对顶角除外),并说明你的理由.
A
B
C
D
E
二、探究新知
解:在
△ABC
和
△ADE
中,
∵ AB∶CD=BC∶DE=AC∶AE,
∴ △ABC∽△ADE.
∴ ∠BAC=∠DAE,∠B=∠D,∠C=∠E.
∴ ∠BAC-∠CAD
=∠DAE-∠CAD
.
∴ ∠BAD=∠CAE.
故图中相等的角有∠BAC=∠DAE,∠B=∠D,∠C=∠E,∠BAD=∠CAE.
三、课堂小结
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.已知
△ABC
和
△DEF,根据下列条件判断它们是否相似.
(1)AB=3,BC=4,AC=6,
DE=6,EF=8,DF=9;
(2)AB=4,BC=8,AC=10,
DE=20,EF=16,DF=8;
(3)AB=12,BC=15,AC=24,
DE=16,EF=20,DF=30.
是
否
否
四、课堂训练
2.如图,在大小为
4×4
的正方形网格中,是相似三角形的是( ).
A.
①
和
②
B.②
和
③
C.
①
和
③
D.②
和
④
①
②
③
④
C
四、课堂训练
3.如图,∠APD=90°,AP=PB=BC=CD,下列结论正确的是( ).
A.△PAB∽△PCA
B.△PAB∽△PDA
C.△ABC∽△DBA
D.△ABC∽△DCA
A
C
B
P
D
C
四、课堂训练
解析:设AP=PB=BC=CD=1,
∵ ∠APD=90°,
∴ AB=
AC=
AD=
∵
AB∶BC=BD∶AB=AD∶AC,
∴ △ABC∽△DBA,故选
C.
四、课堂训练
4.根据下列条件,判断△ABC
与△A′B′C′
是否相似:
AB=4
cm,BC=6
cm,AC=8
cm,A′B′=12
cm,B′C′=18
cm,A′C′=21
cm.
答案:不相似.
四、课堂训练
5.如图,△ABC
中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
四、课堂训练
证明:∵△ABC
中,点
D,E,F
分别是
AB,BC,CA的中点,
∴
∴
∴ △ABC∽△EFD.
四、课堂训练
6.如图,某地四个乡镇
A,B,C,D
之间建有公路,已知
AB=14
千米,AD=28
千米,BD=21
千米,DC=31.5
千米,公路
AB
与
CD
平行吗?说出你的理由.
A
C
B
D
28
14
21
42
31.5
四、课堂训练
解:公路
AB
与
CD
平行.
∴
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC,
∴ AB∥DC.
五、作业
教科书第
34
页练习第
2,3
题.
教科书第
42
页习题
27.2
第
1,2
题.
第二十七章 相似
27.2.1 相似三角形的判定
第三课时 两边成比例且夹角相等的
两个三角形相似
一、情景导入
1.回忆我们学习过的判定三角形相似的方法.类比证明三角形全等的方法,猜想证明三角形相似还有哪些方法?
2.类似于判定三角形全等的
SAS
方法,能不能通过两边和夹角来判定两个三角形相似呢?
二、探究新知
用刻度尺和量角器画
△ABC
和
△A′B′C′,使∠A=∠A′,
量出
BC
及
B′C′
的长,它们的比值等于
k
吗?再量一量两个三角形另外的两个角,你有什么发现?△ABC
与
△A′B′C′
有何关系?
改变
k
和∠A
的值的大小,是否有同样的结论?
二、探究新知
如图,在
△ABC
与
△A′B′C′
中,已知
∠A=∠A′,求证:△ABC∽△A′B′C′.
证明:在
△A′B′C′
的边
A′B′
上
截取点
D,使
A′D=AB.过点
D
作
DE∥B′C′,交
A′C′
于点
E.
∵ DE∥B′C′,
∴ △A′DE∽△A′B′C′.
∴
B
A
C
D
E
B'
A'
C'
二、探究新知
∵ A′D=AB,
∴
∴ A′E=AC.
又 ∠A′=∠A.
∴ △A′DE
≌
△ABC,
∴ △A′B′C′
∽
△ABC.
二、探究新知
归纳:
由此得到利用两边和夹角来判定三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
符号语言:
∵ ∠A=∠A′,
∴ △ABC
∽
△A′B′C′.
B
A
C
B'
A'
C'
二、探究新知
思考:对于
△ABC
和
△A′B′C′,如果
A′B′∶AB=A′C′∶AC.∠B=∠B′,这两个三角形一定会相似吗?
不会,如下图,因为不能证明构造的三角形和原三角形全等.
A
B
C
A′
B′
B″
C′
二、探究新知
结论:如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似,相等的角一定要是两条对应边的夹角.
二、探究新知
例
1 根据下列条件,判断△ABC
和△A′B′C′
是否相似,并说明理由:
∠A=120°
,AB=7
cm,AC=14
cm,
∠A′=120°,A′B′=3
cm
,A′C′=6
cm.
解:∵
∴
又 ∠A′=∠A,
∴ △ABC
∽
△A′B′C′.
二、探究新知
例
2 如图,△ABC
与△ADE
都是等腰三角形,AD=AE,AB=AC,∠DAB=∠CAE.求证:△ABC
∽△ADE.
证明:∵ △ABC
与
△ADE
是等腰三角形,
∴ AD=AE,AB=AC,
∴
又∵ ∠DAB=∠CAE,
∴ ∠DAB
+∠BAE=∠CAE
+∠BAE,
即 ∠DAE=∠BAC,
∴ △ABC
∽
△ADE.
A
B
C
D
E
二、探究新知
例
3 如图,D,E
分别是△ABC
的边
AC,AB
上的点,AE=1.5,AC=2,BC=3,且
求
DE
的长.
A
C
B
E
D
二、探究新知
解:∵ AE=1.5,AC=2,
∴
又∵ ∠EAD=∠CAB,
∴
△ADE
∽△ABC,
∴
∴
二、探究新知
例
4 如图,
在△ABC
中,CD
是边
AB
上的高,且
求证
∠ACB=90°.
A
B
C
D
二、探究新知
证明:
∵ CD
是边
AB
上的高,
∴ ∠ADC=∠CDB=90°.
∵
∴ △ADC
∽△CDB.
∴ ∠ACD=∠B,
∴ ∠ACB=∠ACD+∠BCD=∠B+∠BCD=90°.
方法总结:解题时需注意隐含条件,如垂直关系,三角形的高等.
三、课堂小结
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.判断.
(1)两个等边三角形相似.
( )
(2)两个直角三角形相似.
( )
(3)两个等腰直角三角形相似.
( )
(4)有一个角是
50°的两个等腰三角形相似.
( )
×
√
√
×
四、课堂训练
2.如图,D
是△ABC
一边
BC
上一点,连接
AD,使
△ABC
∽
△DBA
的条件是( ).
A.AC∶BC=AD∶BD
B.AC∶BC=AB∶
AD
C.AB2=CD
·
BC
D.AB2=BD
·
BC
A
B
C
D
D
四、课堂训练
3.如图△AEB
和△FEC_______
(填“相似”或“不相似”).
54
30
36
45
E
A
F
C
B
相似
四、课堂训练
4.如图,已知△ABC
中,D
为边
AC
上一点,P
为边
AB
上一点,AB=12,AC=8,AD=6,当
AP
的长度为
_______
时,△ADP
和△ABC
相似.
A
B
C
D
4
或
9
四、课堂训练
解:当△ADP
∽△ACB
时,
AP∶AB=AD∶AC
,
∴ AP∶12=6∶8.
解得
AP=9;
当△ADP
∽△ABC
时,
AD∶AB=AP∶AC,
∴ 6∶12=AP∶8,
解得
AP=4.
∴ 当
AP
的长度为
4
或
9
时,△ADP
和△ABC
相似.
A
B
C
D
P
P
四、课堂训练
5.如图,在四边形
ABCD
中,已知
∠B=∠ACD,
AB=6,BC=4,AC=5,CD=
,求
AD
的长.
A
B
C
D
四、课堂训练
解:∵ AB=6,BC=4,AC=5,CD=
,
∴
又∵ ∠B=∠ACD,
∴ △ABC
∽
△DCA,
∴
∴
四、课堂训练
6.如图,∠DAB=∠CAE,且
AB·AD=AE·AC,求证
△ABC
∽△AED.
证明:∵ AB
·
AD=AE
·
AC,
∴
又∵ ∠DAB=∠CAE,
∴ ∠
DAB+∠BAE=∠CAE+∠BAE,
即 ∠DAE=∠BAC,
∴
△ABC
∽△AED.
A
B
C
D
E
五、作业
教科书第
42
页习题
27.
2
第
3
题.
第二十七章 相似
27.2.1 相似三角形的判定
第四课时 两角分别相等的两个三角形相似
一、情景导入
学校举办活动,需要三个内角分别为
90°,60°,30°的形状相同,大小不同的三角纸板若干.小明手上的测量工具只有一个量角器,他该怎么做呢?
?
?
?
二、探究新知
与同伴合作,一人画△ABC,另一人画△A′B′C′,使∠A=∠A′,∠B=∠B′,探究下列问题:
问题一 度量
AB,BC,AC,A′B′,B′C′,A′C′
的长,并计算出它们的比值.你有什么发现?
C
A
B
A'
B'
C'
二、探究新知
问题二 试证明△A′B′C′∽△ABC.
证明:在△ABC
的边
AB(或
AB
的延长线)上,截取
AD=A′B′,过点
D
作
DE∥BC,交
AC
于点
E,则有△ADE
∽△ABC,∠ADE=∠B.
∵ ∠B=∠B′,
∴ ∠ADE=∠B′.
又∵
AD=A′B′,∠A=∠A′,
∴ △ADE
≌△A′B′C′.
∴ △A′B′C′
∽△ABC.
C
A
A'
B
B'
C'
D
E
二、探究新知
归纳:
由此得到利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A',∠B=∠B',
∴ △ABC∽△A'B'C'.
C
A
B
A'
B'
C'
二、探究新知
例
1 如图,△ABC
和△DEF
中,∠A=40°,∠B=80°,∠E=80°,∠F=60°.求证:△ABC
∽△DEF.
证明:∵ 在
△ABC
中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A-∠B=60°.
∵ 在
△DEF
中,
∠E=80°,
∠F=60°.
∴ ∠B=∠E
,
∠C=∠F.
∴ △ABC
∽△DEF.
A
C
B
F
E
D
二、探究新知
例
2 如图,弦
AB
和
CD
相交于
⊙O
内一点
P,求证:PA·PB=PC·PD.
证明:连接
AC,DB.
∵ ∠A
和
∠D
都是弧
CB
所对的圆周角,
∴ ∠A=
_______.
同理 ∠C=
_______,
∴ △PAC
∽
△PDB.
∴ __________
即
PA·PB=PC·PD.
∠D
∠B
O
D
C
B
A
P
三、课堂小结
两角分别相等的两个三角形相似
利用两角判定三角形相似
相似三角形的判定定理的运用
四、课堂训练
1.如图,在△ABC
和△A'B'C'中,若∠A=60°,∠B=40°,∠A'=60°,当∠C'=_____时,△ABC
∽△A'B'C'.
80°
C
A
B
B'
C'
A'
四、课堂训练
2.如图,△ABC
中,AE
交
BC
于点
D,∠C=∠E,AD∶DE=3∶5,AE=8,BD=4,则
DC
的长等于( ).
A.
B.
C.
D.
A
C
A
B
D
E
四、课堂训练
3.如图,点
D
在
AB
上,当∠_______
=∠_______
(或∠_______
=∠_______
)时,
△ACD∽△ABC.
ACD
B
ACB
ADB
A
B
D
C
四、课堂训练
4.如图,⊙O
的弦
AB,CD
相交于点
P,若
PA=3,
PB=8,PC=4,则
PD=____.
6
O
D
C
B
A
P
四、课堂训练
5.如图,△ABC
中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
证明:∵ DE∥BC,
EF∥AB,
∴ ∠AED=∠C,
∵ ∠A=∠FEC.
∴ △ADE∽△EFC.
A
E
F
B
C
D
五、作业
教科书第
36
页练习第
1
题.
教科书第
57
页复习题
27
第
1,2,3题.
第二十七章 形似
27.2.1 相似三角形的判定
第五课时 直角三角形相似的判定
一、情景导入
1.
回忆我们学习过的判定三角形相似的方法.
2.类似于判定三角形全等的方法,能不能通过直角边与斜边来判定两个三角形相似呢?
二、探究新知
利用两组角判定两个三角形相似的定理:
两角分别相等的两个三角形相似.
符号语言:
∵ ∠A=∠A'
,∠B=∠B',
∴ △ABC
∽
△A'B'C'.
C
A
B
A'
B'
C'
二、探究新知
归纳:由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
二、探究新知
思考:对于两个直角三角形,我们还可以用
“HL”判定它们全等.那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
二、探究新知
证明:设______________=k,则
AB=kA′B′,AC=kA′B′.由__________
,得
∴
∴ Rt
△ABC
∽
Rt
△A′B′C′.
C
A
A'
B
B'
C'
勾股定理
二、探究新知
归纳:由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
二、探究新知
例
1 如图,在
Rt△ABC
中,∠C=90°,AB=10,AC=8.E
是
AC
上一点,AE=5,ED⊥AB,垂足为
D.
求AD
的长.
解:∵ ED⊥AB,
∴ ∠EDA=90°.
又 ∠C=90°,∠A=∠A,
D
A
B
C
E
二、探究新知
∴ △AED
∽△ABC.
∴
∴
二、探究新知
例
2 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
,当
AB
的长为____________时,△ACB
与
△ADC相似.
C
A
B
D
二、探究新知
解析:∵ ∠ADC=90°,AD=2,CD=
,
∴
要使这两个直角三角形相似,有两种情况:
(1)当
Rt△ABC
∽
Rt△ACD
时,有
AC
:
AD=AB∶AC,即
∶2=AB∶
,解得
AB=3;
(2)当
Rt△ACB
∽
Rt△CDA
时,有
AC
:
CD=AB∶AC,
即
∶
=AB∶
,解得
AB=
∴ 当
AB
的长为
3
或
时,这两个直角三角形相似.
三、课堂小结
两角分别相等的两个三角形相似
相似三角形的判定定理的运用
直角三角形相似的判定
四、课堂训练
1.在
Rt△ABC
和
Rt△A′B′C′
中,∠C=∠C′=90°
,依据下列各组条件判定这两个三角形是否相似.
(1)∠A=35°
,∠B′=55°:_______
;
(2)AC=3,BC=4,A′C′=6,B′C′=8:_______
;
(3)AB=10,AC=8,A′B′=25,B′C′=15:_______
.
相似
相似
相似
四、课堂训练
2.如图,已知
AB∥DE,∠AFC=∠E,则图中相似三角形共有( ).
A.1对
B.2对
C.3对
D.4对
C
四、课堂训练
3.如图,在
Rt△ABC
中,∠ABC=90°,BD⊥AC于D.若
AB=6,AD=2,则
AC=_______
,BD=_______
,BC=_______
.
D
B
C
A
18
四、课堂训练
4.如图,△ABC
的高
AD,BE
交于点
F.
求证:
D
C
A
B
E
F
四、课堂训练
证明:
∵ △ABC
的高
AD,BE
交于点
F,
∴ ∠FEA=∠FDB=90°,
∠AFE=∠BFD(对顶角相等).
∴ △FEA
∽
△
FDB,
∴
四、课堂训练
5.如图,∠1=∠2=∠3,求证:△ABC
∽△ADE.
证明:∵ ∠BAC=∠1+∠DAC,
∠DAE=∠3+∠DAC,∠1=∠3,
∴
∠BAC=∠DAE.
∵
∠C=180°-∠2-∠DOC
,
∠E=180°-∠3-∠AOE,
∠DOC
=∠AOE(对顶角相等),
∴
∠C=∠E.
∴
△ABC∽△ADE.
A
B
C
D
E
1
3
2
O
四、课堂训练
6.如图,BE
是
△ABC
的外接圆
O
的直径,CD
是△ABC
的高,
求证:AC·BC=BE·CD.
证明:
连接
CE,则∠A=∠E.
又∵ BE
是
△ABC
的外接圆
O
的直径,
∴ ∠BCE=90?=∠ADC.
∵ ∠A=∠E,∠BCE=∠ADC,
∴ △ACD∽△EBC.
∴
∴
AC·BC=BE·CD.
O
D
C
B
A
E
五、作业
教科书第
36
页练习第
2,3
题.
