27. 3 位似 课件(共2课时 54张)
文档属性
| 名称 | 27. 3 位似 课件(共2课时 54张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览







文档简介
(共54张PPT)
第二十七章 相似
27.
3 位似
第一课时 位似图形的概念及画法
一、情景导入
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
二、探究新知
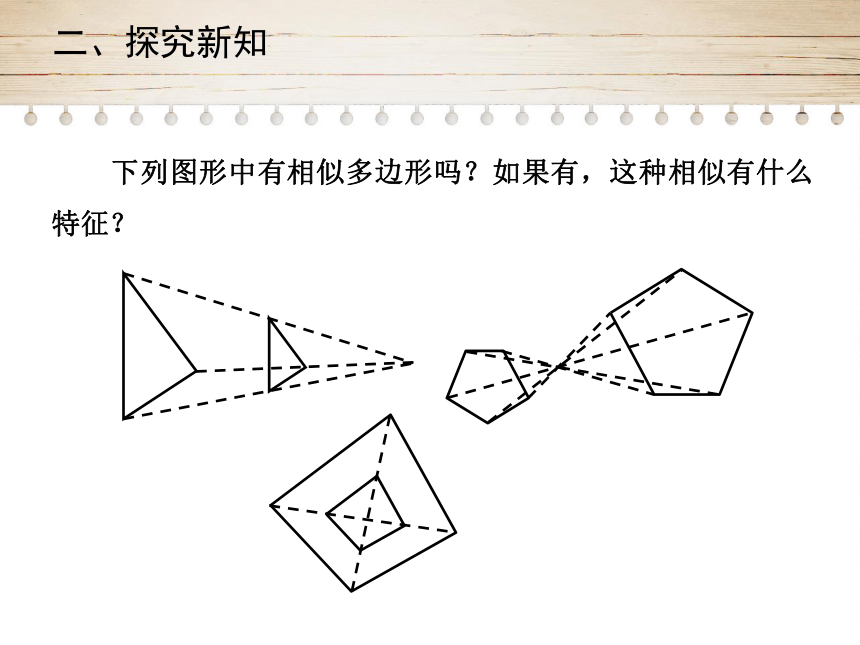
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
二、探究新知
归纳:
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
判断两个图形是不是位似图形,需要从两方面去考察:一是这两个图形是相似的,二是要有特殊的位置关系,即每组对应点所在的直线都经过同一点.
二、探究新知
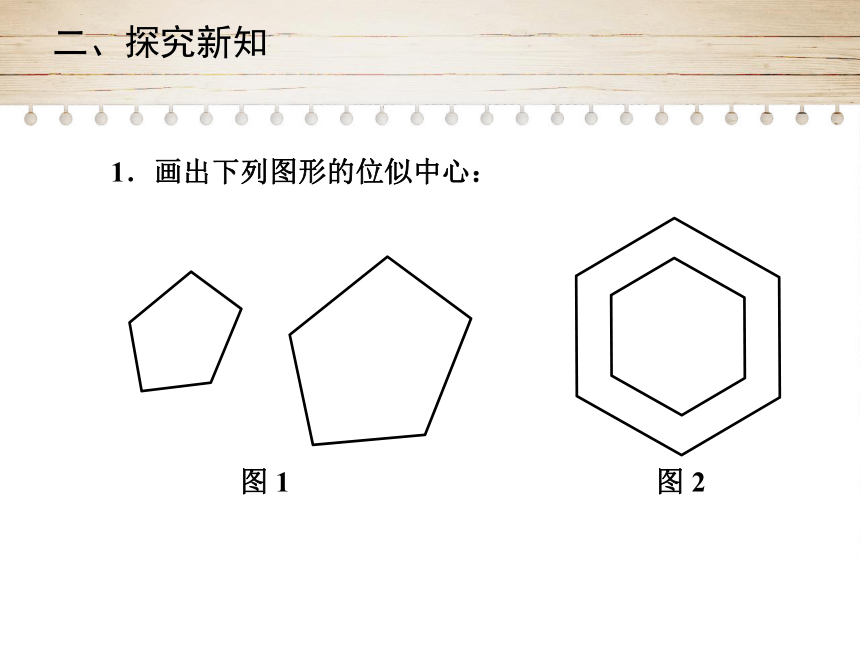
1.画出下列图形的位似中心:
图
1
图
2
二、探究新知
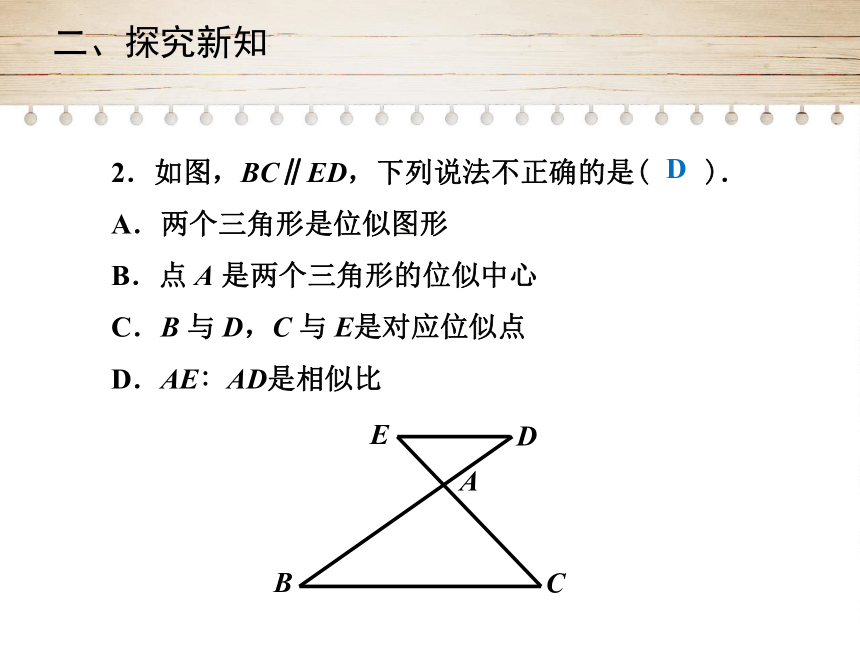
2.如图,BC∥ED,下列说法不正确的是( ).
A.两个三角形是位似图形
B.点
A
是两个三角形的位似中心
C.B
与
D,C
与
E是对应位似点
D.AE∶AD是相似比
D
E
A
B
C
D
二、探究新知
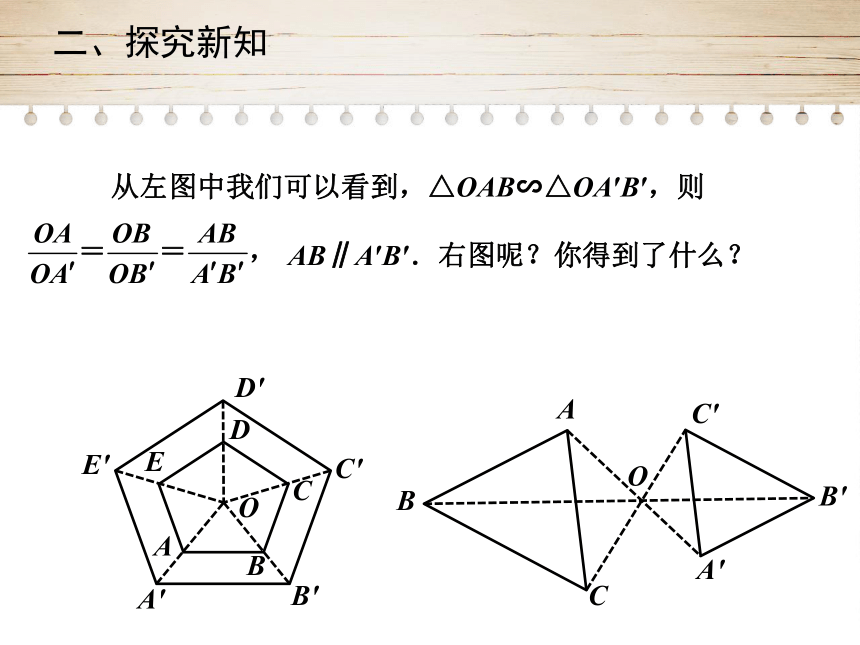
从左图中我们可以看到,△OAB∽△OA′B′,则
AB∥A′B′.右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
二、探究新知
归纳:
1.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2.位似图形上任意一对对应点到位似中心的距离之比
等于相似比.(位似图形的相似比也叫做位似比)
3.对应线段平行或者在一条直线上.
二、探究新知
如图,四边形木框
ABCD
在灯泡发出的光照射下形成的影子是四边形
A′B′C′D′,若
OB∶O′B′=1∶2,则四边形
ABCD
的面积与四边形
A′B′C′D′
的面积比为( ).
A.4∶1 B.
∶1 C.1∶
D.1∶4
D
二、探究新知
例
1 把四边形
ABCD
缩小到原来的
(1)在四边形外任选一点
O(如图);
(2)分别在线段
OA、OB、OC、OD
上取点
A',B',C',D',使得
(3)顺次连接点
A',B',C',D',所得四边形
A'B'C'D'就是所要求的图形.
二、探究新知
O
D
A
B
C
A'
B'
C'
D'
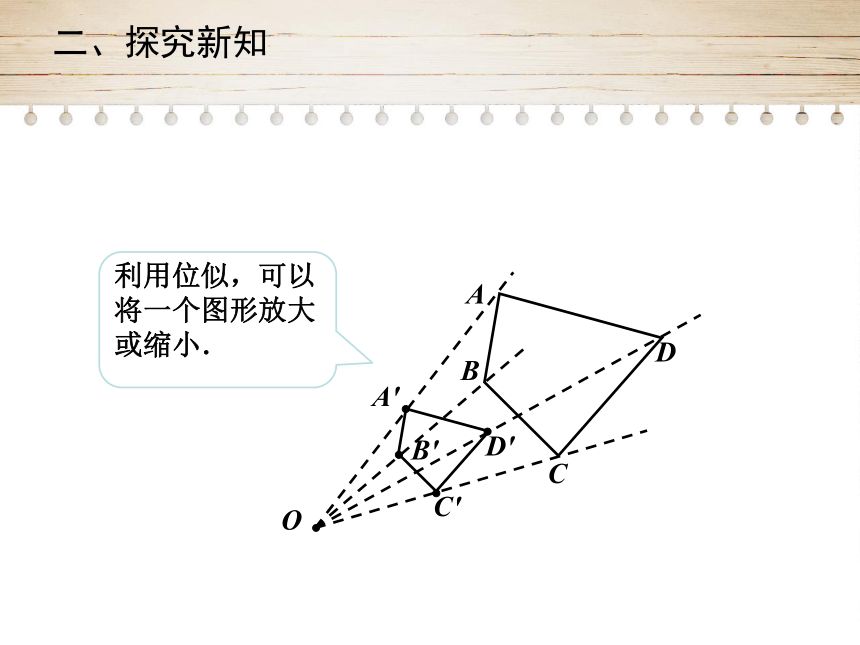
利用位似,可以将一个图形放大或缩小.
二、探究新知
思考:
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点
O,分别在
OA,OB,OC,OD
的反向延长线上取
A′,B′,C′,D′,使得
呢?如果点
O
取在四边形
ABCD
内部呢?分别画出这时得到的图形.
二、探究新知
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
二、探究新知
例
2 如图,△ABC.根据要求作
△A'B'C',使
△A
′B
′C
′∽△ABC,且相似比为
1∶5.
(1)位似中心在
△ABC
的一条边
AB
上;
假设位似中心点
O
为
AB
中点,点
O
位置如图所示.
根据相似比可确定
A′,
B′,C′
的位置.
A
C
B
O
●
A′
B′
C′
●
●
●
二、探究新知
(2)以点
C
为位似中心.
C
A
B
A′
B′
(
C′
)
●
●
●
二、探究新知
归纳:画位似图形的一般步骤:
①
确定位似中心;
②
分别连接并延长位似中心和能代表原图的关键点;
③
根据相似比,确定能代表所作的位似图形的关键点;
④
顺次连接上述各点,得到放大或缩小的图形.
二、探究新知
归纳:
利用位似进行作图的关键是确定位似中心和关键点.
位似分为内位似和外位似,内位似的位似中心在连接两个对应点的线段上;外位似的位似中心在连接两个对应点的线段之外.
三、课堂小结
位似的概念及画法
位似图形的概念
位似图形的性质
画位似图形
四、课堂训练
1.选出下面不同于其他三组的图形( ).
A.
B.
C.
D.
B
四、课堂训练
2.如图,正五边形
FGHMN
与正五边形
ABCDE
是位似图形,若AB∶FG=2∶3,则下列结论正确的是( ).
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
B
A
B
E
C
D
N
F
G
H
M
四、课堂训练
3.下列说法:
①
位似图形一定是相似图形;②
相似图形一定是位似图形;③
两个位似图形若全等,则位似中心在两个图形之间;④
若五边形
ABCDE
与五边形
A′B′C′D′E′
位似,则其中
△ABC
与
△A′B′C′
也是位似的,且位似比相等.其中正确的有_______
.
①④
四、课堂训练
4.如图,△ABC
与△DEF
是位似图形,位似比为
2∶3,已知
AB=4,则
DE
的长为_____.
6
四、课堂训练
5.如图,以
O
为位似中心,将
△ABC
放大为原来的
2
倍.
解:(1)作射线
OA
,OB
,
OC;
(2)分别在
OA,OB
,OC
上取
点
A'
,B'
,C'
,使得
(3)顺次连接
A',B',C'
就是所要求图形.
O
A
B
C
A'
B'
C'
四、课堂训练
6.如图,F
在
BD
上,BC,AD
相交于点
E,且
AB∥CD∥EF.
(1)图中有哪几对位似三角形?选其中一对加以证明;
(2)若
AB=2,CD=3,求
EF
的长.
四、课堂训练
解:(1)△DFE
与
△DBA,△BFE
与
△BDC,△AEB
与
△DEC
都是位似图形;证明略.
(2)∵ △BFE∽△BDC,△AEB∽△DEC,AB=2,CD=3,
∴
∴
解得
五、作业
教科书第
51
页习题
27.
3
第
2,3,4
题.
第二十七章 相似
27.
3 位似
第二课时 平面直角坐标系中的位似
一、情景导入
1.两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做_____________,这个交点叫做_____________.位似图形上任意一对对应点到位似中心的距离之比等于_________________,对应线段
____________________
.
2.如何判断两个图形是不是位似图形?
位似图形
位似中心
相似比(或位似比)
平行或者在一条直线上
一、情景导入
3.画位似图形的一般步骤有哪些?
4.基本模型:
一、情景导入
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
二、探究新知
1.在平面直角坐标系中,有两点
A(6,3),B(6,0).以原点
O
为位似中心,相似比为
,把线段
AB
缩小,观察对应点之间坐标的变化.
二、探究新知
如图,把
AB
缩小后
A,B
的对应点为
A
′( ,)
,B′( ,
);A′′( , ),
B′′(
, ).
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
2
1
2
0
-2
-1
-2
0
二、探究新知
2.
△ABC
三个顶点坐标分别为
A(2,3),B(2,1),C(5,2),以点
O
为位似中心,相似比为
2,将△ABC
放大,观察对应顶点坐标的变化.
二、探究新知
如图,把
△ABC
放大后
A,B,C
的对应点为
A'
(
,
),B'(
,
),C'(
,
);A"
(
,
),B"(
,
),C"(
,
).
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
二、探究新知
问题
1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题
2 所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
二、探究新知
归纳:
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.当位似图形在原点同侧时,其对应顶点的坐标的比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.
3.当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1
时,图形缩小为原来的
k
倍.
二、探究新知
至此,我们已经学习了四种变换:平移,轴对称,旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗?
二、探究新知
例
1 如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A(-2,4),B(-2,0),O(0,0).以原点
O
为位似中心,画出一个三角形使它与△ABO
的相似比为
3∶2.
B
2
4
6
2
-2
-4
x
y
A
O
提示:画三角形关键是确定它各顶点的坐标.根据前面的归纳可知,点
A
的对应点
A′
的坐标为
即(-3,6),类似地,可以确定其他顶点的坐标.
二、探究新知
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
二、探究新知
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′(-3,0),O(0,0).顺次连接点
A′,B′,O,所得的
△A′B′O
就是要画的一个图形.
二、探究新知
还有其他画法吗?自己试一试.
三、课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
坐标变化规律
平面直角坐标系中的位似图形的画法
四、课堂训练
1.将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是( ).
A.将各点的纵坐标乘以
2,横坐标不变
B.将各点的横坐标除以
2,纵坐标不变
C.将各点的横坐标,纵坐标都乘以
2
D.将各点的纵坐标减去
2,横坐标加上
2
C
四、课堂训练
2.如图,小朋在坐标系中以
A
为位似中心画了两个位似的直角三角形,可不小心把
E
点弄脏,则
E
点坐标为( ).
A.(4,-3)
B.(4,-2)
C.(4,-4)
D.(4,-6)
A
四、课堂训练
3.如图所示,某学习小组在讨论
“变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点(a,b)对应大鱼上的点______________.
(-2a,-2b)
四、课堂训练
4.原点
O
是△ABC
和△A′B′C′
的位似中心,点
A(1,
0)与点
A′(-2,0)是对应点,△ABC
的面积
,则△A′B′C′
的面积是_______.
6
四、课堂训练
5.如图,正方形
ABCD
和正方形
OEFG
中,点
A
和点
F
的坐标分别为(3,2),(-1,-1),则两个正方形的位似中心的坐标是___________________.
(1,0)或
(-5,-2)
四、课堂训练
6.△ABC
三个顶点坐标分别为
A(2,-2),B(4,-5)
,C(5,-2),以原点
O
为位似中心,将这个三角形放大为原来的
2
倍.
四、课堂训练
答案:
A'
(4,-4),
B'(8,-10),
C'
(10,-4);
A″(-4,4),
B″(-8,10),
C″(-10,4).
C
2
4
6
-4
x
y
A
B
2
-2
B'
A'
C'
A"
B"
C"
四、课堂训练
7.在
13×13
的网格图中,已知△ABC
和点
M
(1,2).
(1)以点
M
为位似
中心,位似比为
2,画
出
△ABC的位似图形
△A′B′C′;
(2)写出△A′B′C′
的各顶点坐标.
x
y
A
B
C
M
四、课堂训练
解:(1)如图所示.
(2)△A′B′C′
的各顶点坐标分别为
A′
(3,6),B′(5,2),C′
(11,4).
x
y
A
B
C
M
A′
B′
C′
四、课堂训练
8.如图,点
A
的坐标为(3,4),点
O
的坐标为(0,0),点
B
的坐标为(4,0).
(1)将△AOB
沿
x
轴向左平移
1
个单位长度后得△A1O1B1,则点
A1
的坐标为_______
,
△A1O1B1
的面积为_______;
(2)将△AOB
绕原点旋转
180?后得△A2O2B2,则点
A2
的坐标为__________;
(2,4)
8
(-3,-4)
4
x
y
A
B
4
3
四、课堂训练
(3)将△AOB
沿
x
轴翻折后得△A3O3B3,则点
A3
的坐标为_____________;
(4)以
O
为位似中心,按比例尺
1
:
2
将△AOB
放大后得△A4O4B4,若点
B
在
x
轴负半轴上,则点
A4
的坐标为
___________,△A4O4B4的面积为_______.
4
x
y
A
B
4
3
(3,-4)
(-6,-8)
32
五、作业
教科书第
51
页习题
27.
3
第
5,6,7
题.
第二十七章 相似
27.
3 位似
第一课时 位似图形的概念及画法
一、情景导入
如图,是幻灯机放映图片的示意图,在幻灯机放映图片的过程中,这些图片之间有什么关系?
连接图片上对应的点,你有什么发现?
二、探究新知
下列图形中有相似多边形吗?如果有,这种相似有什么特征?
二、探究新知
归纳:
两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
判断两个图形是不是位似图形,需要从两方面去考察:一是这两个图形是相似的,二是要有特殊的位置关系,即每组对应点所在的直线都经过同一点.
二、探究新知
1.画出下列图形的位似中心:
图
1
图
2
二、探究新知
2.如图,BC∥ED,下列说法不正确的是( ).
A.两个三角形是位似图形
B.点
A
是两个三角形的位似中心
C.B
与
D,C
与
E是对应位似点
D.AE∶AD是相似比
D
E
A
B
C
D
二、探究新知
从左图中我们可以看到,△OAB∽△OA′B′,则
AB∥A′B′.右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
二、探究新知
归纳:
1.位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2.位似图形上任意一对对应点到位似中心的距离之比
等于相似比.(位似图形的相似比也叫做位似比)
3.对应线段平行或者在一条直线上.
二、探究新知
如图,四边形木框
ABCD
在灯泡发出的光照射下形成的影子是四边形
A′B′C′D′,若
OB∶O′B′=1∶2,则四边形
ABCD
的面积与四边形
A′B′C′D′
的面积比为( ).
A.4∶1 B.
∶1 C.1∶
D.1∶4
D
二、探究新知
例
1 把四边形
ABCD
缩小到原来的
(1)在四边形外任选一点
O(如图);
(2)分别在线段
OA、OB、OC、OD
上取点
A',B',C',D',使得
(3)顺次连接点
A',B',C',D',所得四边形
A'B'C'D'就是所要求的图形.
二、探究新知
O
D
A
B
C
A'
B'
C'
D'
利用位似,可以将一个图形放大或缩小.
二、探究新知
思考:
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点
O,分别在
OA,OB,OC,OD
的反向延长线上取
A′,B′,C′,D′,使得
呢?如果点
O
取在四边形
ABCD
内部呢?分别画出这时得到的图形.
二、探究新知
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
A'
B'
C'
D'
二、探究新知
例
2 如图,△ABC.根据要求作
△A'B'C',使
△A
′B
′C
′∽△ABC,且相似比为
1∶5.
(1)位似中心在
△ABC
的一条边
AB
上;
假设位似中心点
O
为
AB
中点,点
O
位置如图所示.
根据相似比可确定
A′,
B′,C′
的位置.
A
C
B
O
●
A′
B′
C′
●
●
●
二、探究新知
(2)以点
C
为位似中心.
C
A
B
A′
B′
(
C′
)
●
●
●
二、探究新知
归纳:画位似图形的一般步骤:
①
确定位似中心;
②
分别连接并延长位似中心和能代表原图的关键点;
③
根据相似比,确定能代表所作的位似图形的关键点;
④
顺次连接上述各点,得到放大或缩小的图形.
二、探究新知
归纳:
利用位似进行作图的关键是确定位似中心和关键点.
位似分为内位似和外位似,内位似的位似中心在连接两个对应点的线段上;外位似的位似中心在连接两个对应点的线段之外.
三、课堂小结
位似的概念及画法
位似图形的概念
位似图形的性质
画位似图形
四、课堂训练
1.选出下面不同于其他三组的图形( ).
A.
B.
C.
D.
B
四、课堂训练
2.如图,正五边形
FGHMN
与正五边形
ABCDE
是位似图形,若AB∶FG=2∶3,则下列结论正确的是( ).
A.2DE=3MN
B.3DE=2MN
C.3∠A=2∠F
D.2∠A=3∠F
B
A
B
E
C
D
N
F
G
H
M
四、课堂训练
3.下列说法:
①
位似图形一定是相似图形;②
相似图形一定是位似图形;③
两个位似图形若全等,则位似中心在两个图形之间;④
若五边形
ABCDE
与五边形
A′B′C′D′E′
位似,则其中
△ABC
与
△A′B′C′
也是位似的,且位似比相等.其中正确的有_______
.
①④
四、课堂训练
4.如图,△ABC
与△DEF
是位似图形,位似比为
2∶3,已知
AB=4,则
DE
的长为_____.
6
四、课堂训练
5.如图,以
O
为位似中心,将
△ABC
放大为原来的
2
倍.
解:(1)作射线
OA
,OB
,
OC;
(2)分别在
OA,OB
,OC
上取
点
A'
,B'
,C'
,使得
(3)顺次连接
A',B',C'
就是所要求图形.
O
A
B
C
A'
B'
C'
四、课堂训练
6.如图,F
在
BD
上,BC,AD
相交于点
E,且
AB∥CD∥EF.
(1)图中有哪几对位似三角形?选其中一对加以证明;
(2)若
AB=2,CD=3,求
EF
的长.
四、课堂训练
解:(1)△DFE
与
△DBA,△BFE
与
△BDC,△AEB
与
△DEC
都是位似图形;证明略.
(2)∵ △BFE∽△BDC,△AEB∽△DEC,AB=2,CD=3,
∴
∴
解得
五、作业
教科书第
51
页习题
27.
3
第
2,3,4
题.
第二十七章 相似
27.
3 位似
第二课时 平面直角坐标系中的位似
一、情景导入
1.两个相似多边形,如果它们对应顶点所在的直线相交于一点,我们就把这样的两个图形叫做_____________,这个交点叫做_____________.位似图形上任意一对对应点到位似中心的距离之比等于_________________,对应线段
____________________
.
2.如何判断两个图形是不是位似图形?
位似图形
位似中心
相似比(或位似比)
平行或者在一条直线上
一、情景导入
3.画位似图形的一般步骤有哪些?
4.基本模型:
一、情景导入
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
二、探究新知
1.在平面直角坐标系中,有两点
A(6,3),B(6,0).以原点
O
为位似中心,相似比为
,把线段
AB
缩小,观察对应点之间坐标的变化.
二、探究新知
如图,把
AB
缩小后
A,B
的对应点为
A
′( ,)
,B′( ,
);A′′( , ),
B′′(
, ).
2
4
6
4
6
B'
-2
-4
-4
x
y
A
B
A'
A"
B"
O
2
1
2
0
-2
-1
-2
0
二、探究新知
2.
△ABC
三个顶点坐标分别为
A(2,3),B(2,1),C(5,2),以点
O
为位似中心,相似比为
2,将△ABC
放大,观察对应顶点坐标的变化.
二、探究新知
如图,把
△ABC
放大后
A,B,C
的对应点为
A'
(
,
),B'(
,
),C'(
,
);A"
(
,
),B"(
,
),C"(
,
).
2
4
6
4
6
-2
-4
-4
x
y
A
B
2
8
10
C
-2
-6
-8
-10
-8
B'
A'
C'
A"
B"
C"
4
6
4
2
10
4
-4
-6
-4
-2
-10
-4
二、探究新知
问题
1 在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?
问题
2 所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
二、探究新知
归纳:
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.当位似图形在原点同侧时,其对应顶点的坐标的比为
k;当位似图形在原点两侧时,其对应顶点的坐标的比为-k.
3.当
k>1
时,图形扩大为原来的
k
倍;当
0<k<1
时,图形缩小为原来的
k
倍.
二、探究新知
至此,我们已经学习了四种变换:平移,轴对称,旋转和位似,你能说出它们之间的异同吗?在右图所示的图案中,你能找到这些变换吗?
二、探究新知
例
1 如图,在平面直角坐标系中,△ABO
三个顶点的坐标分别为
A(-2,4),B(-2,0),O(0,0).以原点
O
为位似中心,画出一个三角形使它与△ABO
的相似比为
3∶2.
B
2
4
6
2
-2
-4
x
y
A
O
提示:画三角形关键是确定它各顶点的坐标.根据前面的归纳可知,点
A
的对应点
A′
的坐标为
即(-3,6),类似地,可以确定其他顶点的坐标.
二、探究新知
2
4
6
2
-2
-4
x
y
A
B
O
A′
B′
二、探究新知
解:利用位似中对应点的坐标的变化规律,分别取点
A′
(-3,6),B′(-3,0),O(0,0).顺次连接点
A′,B′,O,所得的
△A′B′O
就是要画的一个图形.
二、探究新知
还有其他画法吗?自己试一试.
三、课堂小结
平面直角坐标系中的位似
平面直角坐标系中的位似变换
坐标变化规律
平面直角坐标系中的位似图形的画法
四、课堂训练
1.将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的是( ).
A.将各点的纵坐标乘以
2,横坐标不变
B.将各点的横坐标除以
2,纵坐标不变
C.将各点的横坐标,纵坐标都乘以
2
D.将各点的纵坐标减去
2,横坐标加上
2
C
四、课堂训练
2.如图,小朋在坐标系中以
A
为位似中心画了两个位似的直角三角形,可不小心把
E
点弄脏,则
E
点坐标为( ).
A.(4,-3)
B.(4,-2)
C.(4,-4)
D.(4,-6)
A
四、课堂训练
3.如图所示,某学习小组在讨论
“变化的鱼”时,知道大鱼与小鱼是位似图形,则小鱼上的点(a,b)对应大鱼上的点______________.
(-2a,-2b)
四、课堂训练
4.原点
O
是△ABC
和△A′B′C′
的位似中心,点
A(1,
0)与点
A′(-2,0)是对应点,△ABC
的面积
,则△A′B′C′
的面积是_______.
6
四、课堂训练
5.如图,正方形
ABCD
和正方形
OEFG
中,点
A
和点
F
的坐标分别为(3,2),(-1,-1),则两个正方形的位似中心的坐标是___________________.
(1,0)或
(-5,-2)
四、课堂训练
6.△ABC
三个顶点坐标分别为
A(2,-2),B(4,-5)
,C(5,-2),以原点
O
为位似中心,将这个三角形放大为原来的
2
倍.
四、课堂训练
答案:
A'
(4,-4),
B'(8,-10),
C'
(10,-4);
A″(-4,4),
B″(-8,10),
C″(-10,4).
C
2
4
6
-4
x
y
A
B
2
-2
B'
A'
C'
A"
B"
C"
四、课堂训练
7.在
13×13
的网格图中,已知△ABC
和点
M
(1,2).
(1)以点
M
为位似
中心,位似比为
2,画
出
△ABC的位似图形
△A′B′C′;
(2)写出△A′B′C′
的各顶点坐标.
x
y
A
B
C
M
四、课堂训练
解:(1)如图所示.
(2)△A′B′C′
的各顶点坐标分别为
A′
(3,6),B′(5,2),C′
(11,4).
x
y
A
B
C
M
A′
B′
C′
四、课堂训练
8.如图,点
A
的坐标为(3,4),点
O
的坐标为(0,0),点
B
的坐标为(4,0).
(1)将△AOB
沿
x
轴向左平移
1
个单位长度后得△A1O1B1,则点
A1
的坐标为_______
,
△A1O1B1
的面积为_______;
(2)将△AOB
绕原点旋转
180?后得△A2O2B2,则点
A2
的坐标为__________;
(2,4)
8
(-3,-4)
4
x
y
A
B
4
3
四、课堂训练
(3)将△AOB
沿
x
轴翻折后得△A3O3B3,则点
A3
的坐标为_____________;
(4)以
O
为位似中心,按比例尺
1
:
2
将△AOB
放大后得△A4O4B4,若点
B
在
x
轴负半轴上,则点
A4
的坐标为
___________,△A4O4B4的面积为_______.
4
x
y
A
B
4
3
(3,-4)
(-6,-8)
32
五、作业
教科书第
51
页习题
27.
3
第
5,6,7
题.
