3.3 轴对称和平移的坐标表示(第2课时) 简单平移的坐标表示 课件(共28张PPT)
文档属性
| 名称 | 3.3 轴对称和平移的坐标表示(第2课时) 简单平移的坐标表示 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:12:24 | ||
图片预览








文档简介
(共28张PPT)
简单平移的坐标表示
第3章
图形与坐标
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握坐标变化与图形平移的关系.
2.能利用点的平移规律将平面图形进行平移.
3.会根据图形上点的坐标的变化,来判定图形的移动过程.
【过程与方法】
经历用坐标表示平移的过程发展学生的形象思维能力和数形结合的意识.
【情感态度】
培养学生探究的兴趣和归纳概括的能力,学会使复杂问题简单化.
【教学重点】
掌握坐标变化与图形平移的关系
【教学难点】
利用坐标变化与图形平移的关系解决实际问题。
复习回顾
1.在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点:
关于x轴对称的点横坐标相等,纵坐标互为相反数.
关于y轴对称的点横坐标互为相反数,纵坐标相等.
2.如何在平面直角坐标系中画一个关于x轴或y轴对称的图形.
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
探究新知
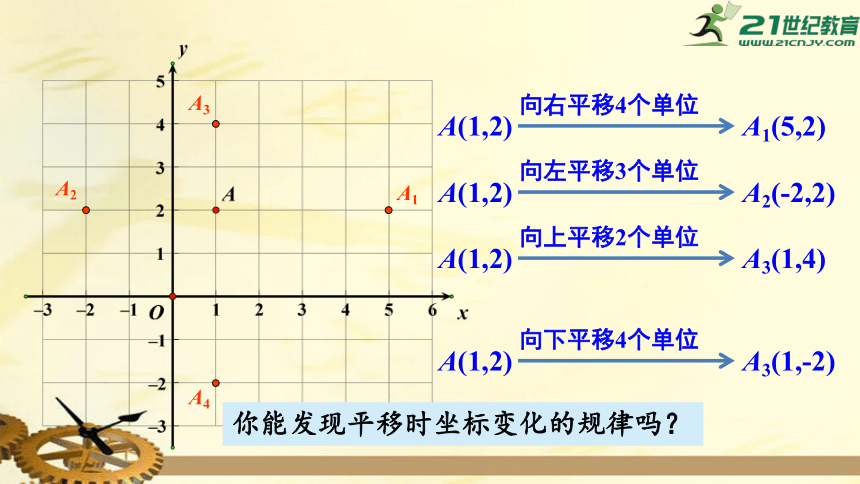
在平面直角坐标系中,A(1,2)分别沿坐标轴方向作以下变换,试作出A的像,并写出像的坐标.
(1)点A向右平移4个单位,像为点A1;
(2)点A向左平移3个单位,像为点A2;
(3)点A向上平移2个单位,像为点A3;
(4)点A向下平移4个单位,像为点A4.
A(1,2)
向右平移4个单位
A1(5,2)
A1
A(1,2)
向左平移3个单位
A2(-2,2)
A2
A(1,2)
向上平移2个单位
A3(1,4)
A3
A(1,2)
向下平移4个单位
A3(1,-2)
A4
你能发现平移时坐标变化的规律吗?
A(1,2)
向右平移4个单位
A1(5,2)
A(1,2)
向左平移3个单位
A2(-2,2)
A(1,2)
向上平移2个单位
A3(1,4)
A(1,2)
向下平移4个单位
A3(1,-2)
一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位,其像的坐标为(a,b+k)(或(a,b-k)).
总结归纳
在如图,线段AB的两个端点坐标分别为A(1,1),B(4,4).
(1)将线段AB向上平移2个单位,作出它的像A′B′,并写出点A′,B′的坐标.
将一个图形整体平移,你要怎么办?
解:将线段AB向上平移2个单位,则线段AB上每一个点都向上平移2个单位,由点A,B的坐标可知其像的坐标是:
点A′(1,3),点B′(4,6),连接点A′,B′,所得线段A′B′即为所求作的像.
A′
B′
A′
B′
(2)若点C(x,
y)是平面内任一点,在上述平移下,像点C(x′,
y′)与点C(x,
y)的坐标有什么关系?
C
解:同理可求出,像点C′与点C之间的坐标关系为:
x′=x
y′=y+2
思考:在坐标系中,将一个点平移,你有什么窍门吗?
上加下减“y”加减,
右加左减“x”加减.
如图,△ABC的顶点坐标分别为A(3,3),B(2,1),C(5,1).
(1)将△ABC向下平移5个单位,作出它的像,并写出像的顶点坐标.
(2)将△ABC向左平移7个单位,作出它的像,并写出像的顶点坐标.
分析:根据平移的性质,将△ABC向下或向左平移k个单位,△ABC的每一个点都向下或向左平移了k个单位,求出顶点A,B,C的像的坐标,作出这些像点,依次连接它们,即可得到△ABC的像.
A1
B1
C1
解(1)将△ABC向下平移5个单位,则横坐标不变,纵坐标减5,由点A,B,C的坐标可知其像的坐标分别是A1(3,-2),B1(2,-4),
C1(5,-4),依次连接点A1,B1,C1,即可得△ABC的像△A1B1C1,如图.
A1
B1
C1
解(2)将△ABC向左平移7
个单位,则横坐标减7,纵坐标不变,由点A,B,C的坐标可知其像的坐标分别是A2(-4,3),B2(-5,1),
C2(-2,1),依次连接点A2,
B2,C2,即可得△ABC的像△A2B2C2,如图.
A2
B2
C2
练习
1.
填空.
(1)点A(-1,2)向右平移2个单位,它的像是点A′_________;
(2)点B(2,-2)向下平移3个单位,它的像是点B′_________.
(1,2)
(2,-5)
2.如图,线段AB的两个端点坐标分别为A(-2,-2),B(2,2).
线段AB向下平移3个单位,它的像是线段A′B′.
(1)试写出点A′,
B′的坐标;
A′
B′
A′(-2,-5)
B′(2,-1)
(2)若点C(x,y)是平面内的任一点,
在上述平移下,
像点C′(x′,y′)与点C(x,y)的坐标之间有什么关系?
A′
B′
解:由(1)可知,像点C′与点C之间的坐标关系为:
x′=x
y′=y-3
3.如图,正方形ABCD的顶点坐标分别为A(2,2),B(2,-2),C(6,-2),D(6,2),将正方形ABCD向左平移4个单位,作出它的像,并写出像的顶点坐标.
A′
B′
C′
D′
A′(-2,2)
B′(-2,-2)
C′(2,-2)
D′(2,2)
随堂练习
1.将点(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是(
)
A.(2,3)
B.(2,-1)
C.(4,1)
D.(0,1)
2.在平面坐标系中,将点(-2,-3)向上平移3个单位,则平移后的点的坐标为_________.
D
(-2,0)
3.将△ABC各顶点的横坐标不变,纵坐标分别加2,连接三个点所成的三角形是由△ABC(
)
A.向左平移2个单位所得
B.向右平移2个单位所得
C.向上平移2个单位所得
D.向下平移2个单位所得
C
4.如图,三角形ABC三个顶点的坐标分别是:A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,点A1,B1,C1坐标分别是什么?并画出相应的三角形A1B1C1;
A1(-2,3)
B1(-3,1)
C1(-5,2)
A1
B1
C1
(2)三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系,为什么?
A1
B1
C1
解:△A1B1C1与△ABC的大小、形状完全相同,△A1B1C1是把△ABC向左平移了6个单位长度所得;
A1
B1
C1
(3)若三角形ABC三个顶点的横坐标都加5,纵坐标不变呢?
解:若三角形ABC三个顶点的横坐标都加5,纵坐标不变,即△ABC向右平移了5个单位长度,所得三角形与原三角形的大小、形状完全相同.
课堂小结
1.点平移的坐标特征.
2.图形的平移方法及平移后顶点坐标的对应关系.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
简单平移的坐标表示
第3章
图形与坐标
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握坐标变化与图形平移的关系.
2.能利用点的平移规律将平面图形进行平移.
3.会根据图形上点的坐标的变化,来判定图形的移动过程.
【过程与方法】
经历用坐标表示平移的过程发展学生的形象思维能力和数形结合的意识.
【情感态度】
培养学生探究的兴趣和归纳概括的能力,学会使复杂问题简单化.
【教学重点】
掌握坐标变化与图形平移的关系
【教学难点】
利用坐标变化与图形平移的关系解决实际问题。
复习回顾
1.在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点:
关于x轴对称的点横坐标相等,纵坐标互为相反数.
关于y轴对称的点横坐标互为相反数,纵坐标相等.
2.如何在平面直角坐标系中画一个关于x轴或y轴对称的图形.
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
探究新知
在平面直角坐标系中,A(1,2)分别沿坐标轴方向作以下变换,试作出A的像,并写出像的坐标.
(1)点A向右平移4个单位,像为点A1;
(2)点A向左平移3个单位,像为点A2;
(3)点A向上平移2个单位,像为点A3;
(4)点A向下平移4个单位,像为点A4.
A(1,2)
向右平移4个单位
A1(5,2)
A1
A(1,2)
向左平移3个单位
A2(-2,2)
A2
A(1,2)
向上平移2个单位
A3(1,4)
A3
A(1,2)
向下平移4个单位
A3(1,-2)
A4
你能发现平移时坐标变化的规律吗?
A(1,2)
向右平移4个单位
A1(5,2)
A(1,2)
向左平移3个单位
A2(-2,2)
A(1,2)
向上平移2个单位
A3(1,4)
A(1,2)
向下平移4个单位
A3(1,-2)
一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位,其像的坐标为(a,b+k)(或(a,b-k)).
总结归纳
在如图,线段AB的两个端点坐标分别为A(1,1),B(4,4).
(1)将线段AB向上平移2个单位,作出它的像A′B′,并写出点A′,B′的坐标.
将一个图形整体平移,你要怎么办?
解:将线段AB向上平移2个单位,则线段AB上每一个点都向上平移2个单位,由点A,B的坐标可知其像的坐标是:
点A′(1,3),点B′(4,6),连接点A′,B′,所得线段A′B′即为所求作的像.
A′
B′
A′
B′
(2)若点C(x,
y)是平面内任一点,在上述平移下,像点C(x′,
y′)与点C(x,
y)的坐标有什么关系?
C
解:同理可求出,像点C′与点C之间的坐标关系为:
x′=x
y′=y+2
思考:在坐标系中,将一个点平移,你有什么窍门吗?
上加下减“y”加减,
右加左减“x”加减.
如图,△ABC的顶点坐标分别为A(3,3),B(2,1),C(5,1).
(1)将△ABC向下平移5个单位,作出它的像,并写出像的顶点坐标.
(2)将△ABC向左平移7个单位,作出它的像,并写出像的顶点坐标.
分析:根据平移的性质,将△ABC向下或向左平移k个单位,△ABC的每一个点都向下或向左平移了k个单位,求出顶点A,B,C的像的坐标,作出这些像点,依次连接它们,即可得到△ABC的像.
A1
B1
C1
解(1)将△ABC向下平移5个单位,则横坐标不变,纵坐标减5,由点A,B,C的坐标可知其像的坐标分别是A1(3,-2),B1(2,-4),
C1(5,-4),依次连接点A1,B1,C1,即可得△ABC的像△A1B1C1,如图.
A1
B1
C1
解(2)将△ABC向左平移7
个单位,则横坐标减7,纵坐标不变,由点A,B,C的坐标可知其像的坐标分别是A2(-4,3),B2(-5,1),
C2(-2,1),依次连接点A2,
B2,C2,即可得△ABC的像△A2B2C2,如图.
A2
B2
C2
练习
1.
填空.
(1)点A(-1,2)向右平移2个单位,它的像是点A′_________;
(2)点B(2,-2)向下平移3个单位,它的像是点B′_________.
(1,2)
(2,-5)
2.如图,线段AB的两个端点坐标分别为A(-2,-2),B(2,2).
线段AB向下平移3个单位,它的像是线段A′B′.
(1)试写出点A′,
B′的坐标;
A′
B′
A′(-2,-5)
B′(2,-1)
(2)若点C(x,y)是平面内的任一点,
在上述平移下,
像点C′(x′,y′)与点C(x,y)的坐标之间有什么关系?
A′
B′
解:由(1)可知,像点C′与点C之间的坐标关系为:
x′=x
y′=y-3
3.如图,正方形ABCD的顶点坐标分别为A(2,2),B(2,-2),C(6,-2),D(6,2),将正方形ABCD向左平移4个单位,作出它的像,并写出像的顶点坐标.
A′
B′
C′
D′
A′(-2,2)
B′(-2,-2)
C′(2,-2)
D′(2,2)
随堂练习
1.将点(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是(
)
A.(2,3)
B.(2,-1)
C.(4,1)
D.(0,1)
2.在平面坐标系中,将点(-2,-3)向上平移3个单位,则平移后的点的坐标为_________.
D
(-2,0)
3.将△ABC各顶点的横坐标不变,纵坐标分别加2,连接三个点所成的三角形是由△ABC(
)
A.向左平移2个单位所得
B.向右平移2个单位所得
C.向上平移2个单位所得
D.向下平移2个单位所得
C
4.如图,三角形ABC三个顶点的坐标分别是:A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,点A1,B1,C1坐标分别是什么?并画出相应的三角形A1B1C1;
A1(-2,3)
B1(-3,1)
C1(-5,2)
A1
B1
C1
(2)三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系,为什么?
A1
B1
C1
解:△A1B1C1与△ABC的大小、形状完全相同,△A1B1C1是把△ABC向左平移了6个单位长度所得;
A1
B1
C1
(3)若三角形ABC三个顶点的横坐标都加5,纵坐标不变呢?
解:若三角形ABC三个顶点的横坐标都加5,纵坐标不变,即△ABC向右平移了5个单位长度,所得三角形与原三角形的大小、形状完全相同.
课堂小结
1.点平移的坐标特征.
2.图形的平移方法及平移后顶点坐标的对应关系.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
