第3章 图形与坐标 小结与复习 课件(共23张PPT)
文档属性
| 名称 | 第3章 图形与坐标 小结与复习 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:26:34 | ||
图片预览





文档简介
(共23张PPT)
小结与复习
第3章
图形与坐标
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生通过复习使学生能掌握用不同的方式确定物体的位置,综合运用图形与坐标的知识解决简单的实际问题.
【过程与方法】
1.参与本章知识梳理与体系构建的过程,培养归纳总结能力.
2.领悟数形结合、分类讨论的思想方法,培养思维的灵活性.
【情感态度】
培养学生良好学习习惯,激发学习兴趣,激发学生对母校的热爱之情.
【教学重点】
特殊点的坐标特征及其在解题中的应用,数形结合的思想.
【教学难点】
感受数形结合的思想.
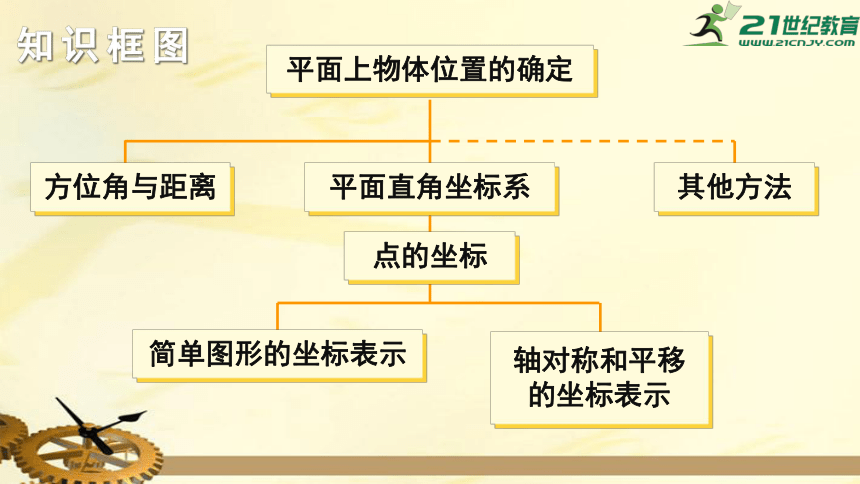
知识框图
平面上物体位置的确定
平面直角坐标系
点的坐标
方位角与距离
其他方法
简单图形的坐标表示
轴对称和平移的坐标表示
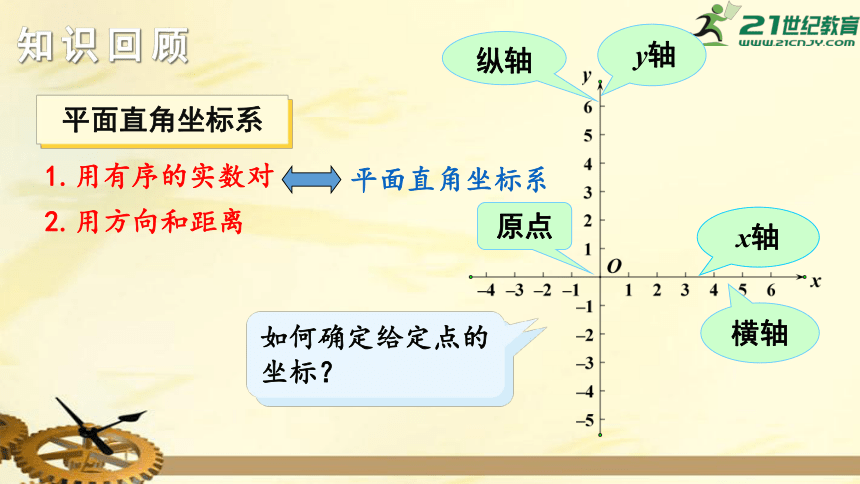
知识回顾
1.用有序的实数对
平面直角坐标系
2.用方向和距离
如何确定给定点的坐标?
原点
纵轴
y轴
横轴
x轴
平面直角坐标系
为了指出坐标(4,2)的点,我们在x轴上找到表示4的点A.
A
过A点作x轴的垂线
再在y轴上找到表示2的点B,过点B作y轴的垂线.
B
P(4,2)
这两条垂线相交于点P,则点P就是坐标(4,2)的点.
点的坐标
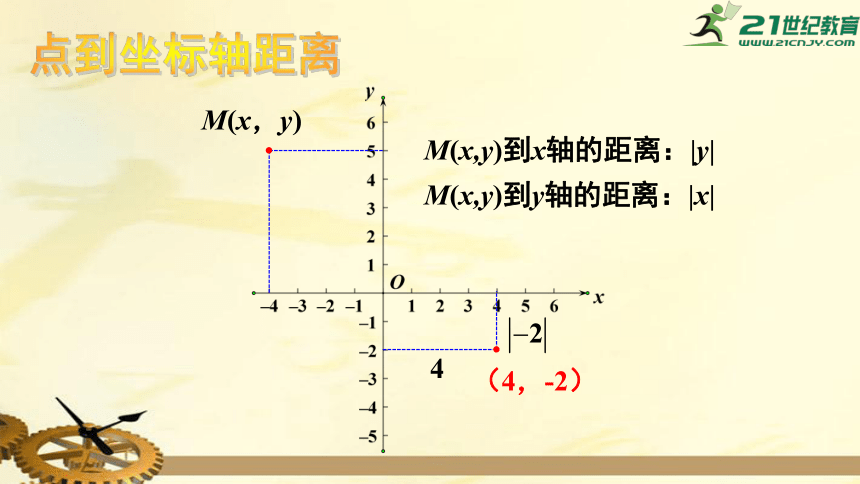
点到坐标轴距离
M(x,y)
(4,-2)
4
M(x,y)到x轴的距离:|y|
M(x,y)到y轴的距离:|x|
特殊点的坐标
C
D
x轴上的点纵坐标都为0,即:(x,0)
平行x轴的直线上的点纵坐标相同.
y轴上的点横坐标都为0,即:(0,y)
平行y轴的直线上的点横坐标相同.
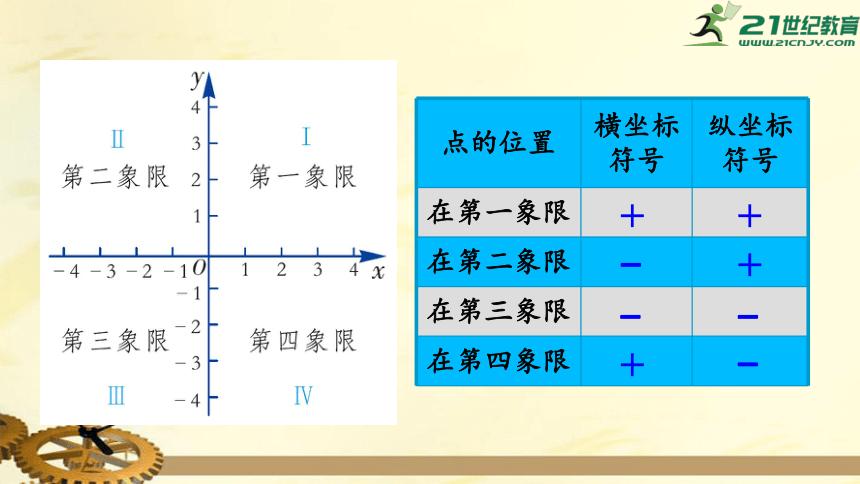
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
+
+
-
+
-
-
+
-
例1.若点P(m,n)在第二象限,则点Q(-m,-n)在第_____象限.
【解析】本题考查象限内点的坐标的符号特征.由点P(m,n)在第二象限,可知m<0,n>0,则点Q(-m,-n)坐标的符号特征为-m>0,-n<0,故点Q在第四象限,填四.
四
在日常生活中,
除了用平面直角坐标系刻画物体之间的位置关系外,有时还可借助方向和距离(或称方位)
来刻画两物体的相对位置.
方位角与距离
李亮家在学校的北偏西60°的方向上,
与学校的距离为1000m;
反过来,学校在李亮家南偏东60°的方向上,与学校的距离为1000m.
我们把北偏西60°,南偏东60°这样的角称为方位角.
平面直角坐标系的构建不同,则点的坐标也不同.在建立直角坐标系时,应使点的坐标简明.
简单图形的坐标表示
轴对称和平移的坐标表示
坐标的变化
图象的变化
(x,
y)
(-x,
y)
关于y轴对称;
(x,
y)
(x,
-y)
关于x轴对称;
(x,
y)
(-x,
-y)
关于原点轴对称;
(x,
y)
(x+m,
y+n)
沿x轴方向平移m个单位,
沿y轴方向平移n个单位.
例2.点M(3,-4)关于x轴的对称点M′的坐标是(
)
A.(3,4)
B.(-3,-4)
C.(-3,4)
D.(-4,3)
【解析】本题考查关于坐标轴对称的点的坐标,关于x轴对称的两个点,横坐标相同,纵坐标互为相反数,故M′(3,4),选A.
A
例3.将点A(4,3)向______________,再______________后得到A′坐标为(-1,5).
【解析】横坐标由4变为-1,减小了5,故向左平移5个单位,纵坐标由3变为5,增加了2,故向上平移2个单位,所以填向左平移5个单位,向上平移2个单位.
左平移5个单位
上平移2个单位
总结归纳
图形平移的方向与距离
图形上点的平移的方向与距离
点平移时
坐标变化规律
图形上点的坐标变化
随堂练习
1.点M(3a-1,1-5a)在y轴上,则M的坐标为_________.
2.点A(a-1,-3)在第四象限,点B(2,b-1)在第一象限,则点P(b,-a)在第______象限.
3.点Q(a,b)到x轴的距离为3,到y轴的距离为4,则符合条件的Q的坐标有(
)
A.1个
B.2个
C.3个
D.4个
D
四
4.如图,将△ABC先向左平移7个单位,再向上平移8个单位,它的像是△A′B′C′,写出△A′B′C′的顶点坐标,并作出该图形.
A′
B′
C′
A′(-3,
6)
B′(-5,
5)
C′(-3,
2)
5.如图,△ABC的坐标分别为A(6,6),B(-3,3),C(3,3),求△ABC的面积.
6.如图,将四边形ABCD各顶点的横坐标、纵坐标分别乘-1,得到的图形与原图形有什么变化?作出坐标变化后的图形,这一过程可以看作是一个什么变换?
A(-6,
3)
B(-6,
1)
C(-2,
1)
D(-2,
5)
A′(6,
-3)
B′(6,
-1)
C′(2,
-1)
D′(2,
-5)
A′
B′
C′
D′
关于原点轴对称.
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
小结与复习
第3章
图形与坐标
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
让学生通过复习使学生能掌握用不同的方式确定物体的位置,综合运用图形与坐标的知识解决简单的实际问题.
【过程与方法】
1.参与本章知识梳理与体系构建的过程,培养归纳总结能力.
2.领悟数形结合、分类讨论的思想方法,培养思维的灵活性.
【情感态度】
培养学生良好学习习惯,激发学习兴趣,激发学生对母校的热爱之情.
【教学重点】
特殊点的坐标特征及其在解题中的应用,数形结合的思想.
【教学难点】
感受数形结合的思想.
知识框图
平面上物体位置的确定
平面直角坐标系
点的坐标
方位角与距离
其他方法
简单图形的坐标表示
轴对称和平移的坐标表示
知识回顾
1.用有序的实数对
平面直角坐标系
2.用方向和距离
如何确定给定点的坐标?
原点
纵轴
y轴
横轴
x轴
平面直角坐标系
为了指出坐标(4,2)的点,我们在x轴上找到表示4的点A.
A
过A点作x轴的垂线
再在y轴上找到表示2的点B,过点B作y轴的垂线.
B
P(4,2)
这两条垂线相交于点P,则点P就是坐标(4,2)的点.
点的坐标
点到坐标轴距离
M(x,y)
(4,-2)
4
M(x,y)到x轴的距离:|y|
M(x,y)到y轴的距离:|x|
特殊点的坐标
C
D
x轴上的点纵坐标都为0,即:(x,0)
平行x轴的直线上的点纵坐标相同.
y轴上的点横坐标都为0,即:(0,y)
平行y轴的直线上的点横坐标相同.
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
+
+
-
+
-
-
+
-
例1.若点P(m,n)在第二象限,则点Q(-m,-n)在第_____象限.
【解析】本题考查象限内点的坐标的符号特征.由点P(m,n)在第二象限,可知m<0,n>0,则点Q(-m,-n)坐标的符号特征为-m>0,-n<0,故点Q在第四象限,填四.
四
在日常生活中,
除了用平面直角坐标系刻画物体之间的位置关系外,有时还可借助方向和距离(或称方位)
来刻画两物体的相对位置.
方位角与距离
李亮家在学校的北偏西60°的方向上,
与学校的距离为1000m;
反过来,学校在李亮家南偏东60°的方向上,与学校的距离为1000m.
我们把北偏西60°,南偏东60°这样的角称为方位角.
平面直角坐标系的构建不同,则点的坐标也不同.在建立直角坐标系时,应使点的坐标简明.
简单图形的坐标表示
轴对称和平移的坐标表示
坐标的变化
图象的变化
(x,
y)
(-x,
y)
关于y轴对称;
(x,
y)
(x,
-y)
关于x轴对称;
(x,
y)
(-x,
-y)
关于原点轴对称;
(x,
y)
(x+m,
y+n)
沿x轴方向平移m个单位,
沿y轴方向平移n个单位.
例2.点M(3,-4)关于x轴的对称点M′的坐标是(
)
A.(3,4)
B.(-3,-4)
C.(-3,4)
D.(-4,3)
【解析】本题考查关于坐标轴对称的点的坐标,关于x轴对称的两个点,横坐标相同,纵坐标互为相反数,故M′(3,4),选A.
A
例3.将点A(4,3)向______________,再______________后得到A′坐标为(-1,5).
【解析】横坐标由4变为-1,减小了5,故向左平移5个单位,纵坐标由3变为5,增加了2,故向上平移2个单位,所以填向左平移5个单位,向上平移2个单位.
左平移5个单位
上平移2个单位
总结归纳
图形平移的方向与距离
图形上点的平移的方向与距离
点平移时
坐标变化规律
图形上点的坐标变化
随堂练习
1.点M(3a-1,1-5a)在y轴上,则M的坐标为_________.
2.点A(a-1,-3)在第四象限,点B(2,b-1)在第一象限,则点P(b,-a)在第______象限.
3.点Q(a,b)到x轴的距离为3,到y轴的距离为4,则符合条件的Q的坐标有(
)
A.1个
B.2个
C.3个
D.4个
D
四
4.如图,将△ABC先向左平移7个单位,再向上平移8个单位,它的像是△A′B′C′,写出△A′B′C′的顶点坐标,并作出该图形.
A′
B′
C′
A′(-3,
6)
B′(-5,
5)
C′(-3,
2)
5.如图,△ABC的坐标分别为A(6,6),B(-3,3),C(3,3),求△ABC的面积.
6.如图,将四边形ABCD各顶点的横坐标、纵坐标分别乘-1,得到的图形与原图形有什么变化?作出坐标变化后的图形,这一过程可以看作是一个什么变换?
A(-6,
3)
B(-6,
1)
C(-2,
1)
D(-2,
5)
A′(6,
-3)
B′(6,
-1)
C′(2,
-1)
D′(2,
-5)
A′
B′
C′
D′
关于原点轴对称.
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
