安徽省安庆市潜山市第四中学2020-2021学年第二学期九年级数学开学检测试题(word版,含答案)
文档属性
| 名称 | 安徽省安庆市潜山市第四中学2020-2021学年第二学期九年级数学开学检测试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:06:46 | ||
图片预览

文档简介
潜山四中2020-2021学年度第二学期开学检测卷
九年级数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.如果两个相似三角形的周长比是1:2,那么它们的面积比是(????)
A. 1:2 B. 1:4 C. 1:2 D. 2:1
2.将y=-(x+4)2+1的图象向右平移2个单位,再向下平移3个单位,所得函数最大值为(????)
523113017780A. y=-2 B. y=2 C. y=-3 D. y=3
3..在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是(????)
A. ① B. ② C. ③ D. ④
52317653263904.根据有关测定,当外界气温与人体正常体温比为黄金比时,人体感到最舒适(人体正常体温约为false),这个气温大约为( )
A.false B.false C.false D.false
5.如图,网格中的两个三角形是位似图形,它们的位似中心是( )
A.点A B.点B C.点C D.点D
53340005549906.已知点false、false均在双曲线上false,且x1<x2,则y1与y2的大小关系是( ?)
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
484124040767032410403587758.如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC,若S△ABD=6,S△ADC=10,则false=( )
A. false B. false C. false D.false
47840903638559.如图,false与false的图象的交点A(-2,-3),B(-1,-6),C(3,2),则不等式false的解集为( )
A. B.
C. D.
501840571501010.如图,抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴交于A、B(3,0)两点,与y轴交于点C,连接AC。有下列四个结论:①bc<0;②b=-2a;③a+b≥am2+bm(m为任意数);④将直线AC向下平移|c|个单位长度得到的直线与直线AC向右平移1个单位长度得到的直线重合。其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,共20分)
11.锐角α满足cosα=false,则cos(90°-α)=______.
12.当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=_ _.
13.如图,在⊙O中,弦AB所对的圆周角∠C=45°,AB=2,BC=1,则∠A=_____°
370268538290514.如图1所示的是公园运动广场的一个漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°。
(1)点A到BC的距离是_ cm;
(2)点D到BC的距离是_ cm.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos60°+4sin60°?tan30°-6cos245°
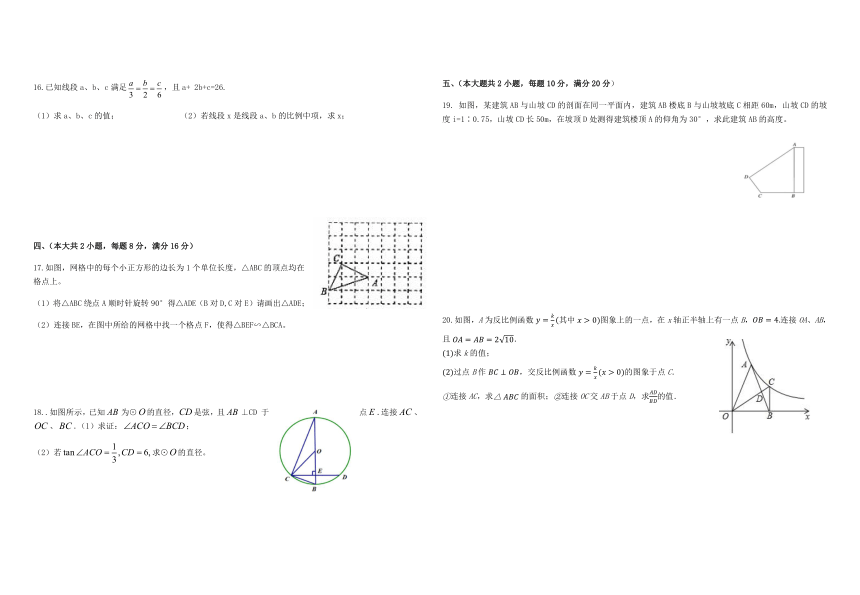
16.已知线段a、b、c满足false,且a+ 2b+c=26.
(1)求a、b、c的值; (2)若线段x是线段a、b的比例中项,求x;
45802552540
四、(本大共2小题,每题8分,满分16分)
17.如图,网格中的每个小正方形的边长为1个单位长度,△ABC的顶点均在格点上。
(1)将△ABC绕点A顺时针旋转90°得△ADE(B对D,C对E)请画出△ADE;
(2)连接BE,在图中所给的网格中找一个格点F,使得△BEF∽△BCA。
18..如图所示,已知false为⊙false的直径,false是弦,且false⊥CD 于点false.连接false、false、false.398970517780(1)求证:false;
(2)若false求⊙false的直径。
五、(本大题共2小题,每题10分,满分20分)
如图,某建筑AB与山坡CD的剖面在同一平面内,建筑AB楼底B与山坡坡底C相距60m,山坡CD的坡度i=1∶0.75,山坡CD长50m,在坡顶D处测得建筑楼顶A的仰角为30°,求此建筑AB的高度。
4888865132080
20.如图,A为反比例函数y=kx(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,4526280120650且OA=AB=210.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=kx(x>0)的图象于点C.
①连接AC,求△ABC的面积;②连接OC交AB于点D,求ADBD的值.
六、(本题满分12分,其中(1)、(2)各6分)
21.如图,在△ABC中,点D,G在边AC上,点E在边BC上,DB=DC,EG∥AB,AE,BD交于点F,BF=AG.
441706026670求证:△BFE∽△CGE;
当∠AEG=∠C时,求证:AB?=AG·AC.
七、(本题满分12分,其中(1)、(2)、(3)各4分)
22.如图,在平面直角坐标系中,已知点A(-1,0)、B(3,0)、C(0,3),抛物线y=ax?+bx+c经过A、B两点。
⑴当该抛物线经过点C时,求该抛物线的解析式;
⑵在⑴的条件下,点P是该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;
4377690105410⑶如果抛物线y=ax?+bx+c的顶点位于△BOC内,求a的取值范围。
八、(本题满分14分,其中(1)4分,(2)6分,(3)4分)
如图,在△ABC中,∠C=90°,AC=2,BC=23,点D是边AC的中点,点P、Q分别是射线BC、BA上的动点,且BQ=32BP,连接PQ、QD、DP。
求证:PQ⊥AB;
如果点P在线段BC上,当△PQD是直角三角形时,求BP的长;
将△PQD沿直线QP翻折,点D的对应点为点D',如果点D'位于△ABC内,请直接写出BP的取值范围
353123567310
九年级开学测试数学参考答案
1-10题
1
2
3
4
5
6
7
8
9
10
B
A
B
A
D
D
B
C
B
C
11-14题 11题:false 12题:10
13题:30° 14题:⑴80false ⑵80false+10
363283513970015题: 0
D
E
16题:⑴a=6 b=4 c=12 ⑵x=2false
17题:见图
18题:
⑴∵直径AB⊥弦CD ∴弧CB=弧BD
∴∠CAB=∠BCD
F
又∵OA=OC ∴∠ACO=∠CAO=∠BCD
⑵∵AB⊥CD CD=6 ∴CE=falseCD=3
∵tan∠ACO=false=tan∠BCD=false ∴BE=1
设OC=OB=R 则OE=R-1 由OC2=CE2+OE2得R=5 ∴⊙O直径=10
19题:
作DE⊥CB于E,DF⊥AB于F
∵iCD=1∶0.75 CD=50 ∴DE=40 EC=30 ∴DF=EB=BC+CE=90
∴AF=DF·tan∠ADF=90·tan30°=30false ∴AB=AF+FB=AF+DE=(40+30false)m
20题:
⑴作AH⊥OB于H,交BC于E
∵AO=AB=2false OB=4 ∴OH=HB=falseOB=2 ∴AH=6 ∴A(2,6) ∴k=2×6=12
⑵①∵BC⊥OB ∴当x=4时,y=false=3 ∴C(4,3) ∴S△ABC=false×3×(4-2)=3
②∵OH=HB EH∥CB ∴EH=falseCB=false ∴AE=6-false=4.5 ∴false=1.5(或false)
21题:
⑴∵DB=DC ∴∠FBE=∠C 又∵EG∥AB AG=BF ∴false∴△CGE∽△BFE
⑵∵∠AEG=∠C ∠EAC=∠CAE ∴△AEG∽△ACE ∴false即AE2=AG·AC
由⑴知∠GEC=∠FEB 又∵EG∥AB ∴∠GEC=∠ABE=∠AEB ∴AB=AE ∴AB2=AG·AC
22题:
⑴∵过A(-1,0) B(3,0) 故设y=a(x+1)(x-3) 又过C(0,3)∴a=-1 ∴y=-(x+1)(x-3)=-x2+2x+3①
⑵设PB与y轴交于点D ∵OB=OC ∴∠OCB=∠OBC ∵∠PBC=∠ACB ∴∠ACO=∠DBO
又∠AOC=∠DOB=90°∴OA=OD ∴D(0,-1) ∴yBP=falsex-1② 联合①②解得x=false y=false
∴P(false , false )
⑶∵y=a(x+1)(x-3)=a(x-1)2-4a ∴顶点(1,-4a) 又∵yBC=-x+3 当x=1时yBC=2
∵0<-4a<2 ∴false<a<0
23题:
⑴∵∠C=90°AC=2 BC=2false ∴AB=4 ∴false=false 又 BQ=falseBP ∴false
又∵∠B公共 ∴△BQP∽△BCA ∴∠BQP=∠C=90°即PQ⊥AB
⑵当∠QPD=90°则PD∥AB 又DA=DC ∴BP=PC=false
当∠QDP=90°作QE⊥AC于E 设PB=x,则BQ=BP·cosB=falsex QA=4-falsex
QE=QA·sinA=false(4-falsex)=2false-falsex AE=QA·cosA=false(4-falsex)=2-falsex
∵∠QED=∠QDP=∠DCP=90°∴△QED∽△DCP ∴false
∴false 即3x2-15falsex+52=0 ∴x=false
又∵∠PQD<90°综上BP=false或false
⑶false<BP<false
九年级数学试卷
一、选择题(本大题共10小题,每小题4分,共40分)
1.如果两个相似三角形的周长比是1:2,那么它们的面积比是(????)
A. 1:2 B. 1:4 C. 1:2 D. 2:1
2.将y=-(x+4)2+1的图象向右平移2个单位,再向下平移3个单位,所得函数最大值为(????)
523113017780A. y=-2 B. y=2 C. y=-3 D. y=3
3..在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是(????)
A. ① B. ② C. ③ D. ④
52317653263904.根据有关测定,当外界气温与人体正常体温比为黄金比时,人体感到最舒适(人体正常体温约为false),这个气温大约为( )
A.false B.false C.false D.false
5.如图,网格中的两个三角形是位似图形,它们的位似中心是( )
A.点A B.点B C.点C D.点D
53340005549906.已知点false、false均在双曲线上false,且x1<x2,则y1与y2的大小关系是( ?)
A.y1<y2 B.y1>y2 C.y1=y2 D.无法确定
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )
A.点(0,3) B.点(1,3) C.点(6,0) D.点(6,1)
484124040767032410403587758.如图,在△ABC中,D为BC上一点,已知AD平分∠BAC,AD=DC,若S△ABD=6,S△ADC=10,则false=( )
A. false B. false C. false D.false
47840903638559.如图,false与false的图象的交点A(-2,-3),B(-1,-6),C(3,2),则不等式false的解集为( )
A. B.
C. D.
501840571501010.如图,抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴交于A、B(3,0)两点,与y轴交于点C,连接AC。有下列四个结论:①bc<0;②b=-2a;③a+b≥am2+bm(m为任意数);④将直线AC向下平移|c|个单位长度得到的直线与直线AC向右平移1个单位长度得到的直线重合。其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4小题,每小题5分,共20分)
11.锐角α满足cosα=false,则cos(90°-α)=______.
12.当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=_ _.
13.如图,在⊙O中,弦AB所对的圆周角∠C=45°,AB=2,BC=1,则∠A=_____°
370268538290514.如图1所示的是公园运动广场的一个漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°。
(1)点A到BC的距离是_ cm;
(2)点D到BC的距离是_ cm.
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos60°+4sin60°?tan30°-6cos245°
16.已知线段a、b、c满足false,且a+ 2b+c=26.
(1)求a、b、c的值; (2)若线段x是线段a、b的比例中项,求x;
45802552540
四、(本大共2小题,每题8分,满分16分)
17.如图,网格中的每个小正方形的边长为1个单位长度,△ABC的顶点均在格点上。
(1)将△ABC绕点A顺时针旋转90°得△ADE(B对D,C对E)请画出△ADE;
(2)连接BE,在图中所给的网格中找一个格点F,使得△BEF∽△BCA。
18..如图所示,已知false为⊙false的直径,false是弦,且false⊥CD 于点false.连接false、false、false.398970517780(1)求证:false;
(2)若false求⊙false的直径。
五、(本大题共2小题,每题10分,满分20分)
如图,某建筑AB与山坡CD的剖面在同一平面内,建筑AB楼底B与山坡坡底C相距60m,山坡CD的坡度i=1∶0.75,山坡CD长50m,在坡顶D处测得建筑楼顶A的仰角为30°,求此建筑AB的高度。
4888865132080
20.如图,A为反比例函数y=kx(其中x>0)图象上的一点,在x轴正半轴上有一点B,OB=4.连接OA、AB,4526280120650且OA=AB=210.
(1)求k的值;
(2)过点B作BC⊥OB,交反比例函数y=kx(x>0)的图象于点C.
①连接AC,求△ABC的面积;②连接OC交AB于点D,求ADBD的值.
六、(本题满分12分,其中(1)、(2)各6分)
21.如图,在△ABC中,点D,G在边AC上,点E在边BC上,DB=DC,EG∥AB,AE,BD交于点F,BF=AG.
441706026670求证:△BFE∽△CGE;
当∠AEG=∠C时,求证:AB?=AG·AC.
七、(本题满分12分,其中(1)、(2)、(3)各4分)
22.如图,在平面直角坐标系中,已知点A(-1,0)、B(3,0)、C(0,3),抛物线y=ax?+bx+c经过A、B两点。
⑴当该抛物线经过点C时,求该抛物线的解析式;
⑵在⑴的条件下,点P是该抛物线上一点,且位于第三象限,当∠PBC=∠ACB时,求点P的坐标;
4377690105410⑶如果抛物线y=ax?+bx+c的顶点位于△BOC内,求a的取值范围。
八、(本题满分14分,其中(1)4分,(2)6分,(3)4分)
如图,在△ABC中,∠C=90°,AC=2,BC=23,点D是边AC的中点,点P、Q分别是射线BC、BA上的动点,且BQ=32BP,连接PQ、QD、DP。
求证:PQ⊥AB;
如果点P在线段BC上,当△PQD是直角三角形时,求BP的长;
将△PQD沿直线QP翻折,点D的对应点为点D',如果点D'位于△ABC内,请直接写出BP的取值范围
353123567310
九年级开学测试数学参考答案
1-10题
1
2
3
4
5
6
7
8
9
10
B
A
B
A
D
D
B
C
B
C
11-14题 11题:false 12题:10
13题:30° 14题:⑴80false ⑵80false+10
363283513970015题: 0
D
E
16题:⑴a=6 b=4 c=12 ⑵x=2false
17题:见图
18题:
⑴∵直径AB⊥弦CD ∴弧CB=弧BD
∴∠CAB=∠BCD
F
又∵OA=OC ∴∠ACO=∠CAO=∠BCD
⑵∵AB⊥CD CD=6 ∴CE=falseCD=3
∵tan∠ACO=false=tan∠BCD=false ∴BE=1
设OC=OB=R 则OE=R-1 由OC2=CE2+OE2得R=5 ∴⊙O直径=10
19题:
作DE⊥CB于E,DF⊥AB于F
∵iCD=1∶0.75 CD=50 ∴DE=40 EC=30 ∴DF=EB=BC+CE=90
∴AF=DF·tan∠ADF=90·tan30°=30false ∴AB=AF+FB=AF+DE=(40+30false)m
20题:
⑴作AH⊥OB于H,交BC于E
∵AO=AB=2false OB=4 ∴OH=HB=falseOB=2 ∴AH=6 ∴A(2,6) ∴k=2×6=12
⑵①∵BC⊥OB ∴当x=4时,y=false=3 ∴C(4,3) ∴S△ABC=false×3×(4-2)=3
②∵OH=HB EH∥CB ∴EH=falseCB=false ∴AE=6-false=4.5 ∴false=1.5(或false)
21题:
⑴∵DB=DC ∴∠FBE=∠C 又∵EG∥AB AG=BF ∴false∴△CGE∽△BFE
⑵∵∠AEG=∠C ∠EAC=∠CAE ∴△AEG∽△ACE ∴false即AE2=AG·AC
由⑴知∠GEC=∠FEB 又∵EG∥AB ∴∠GEC=∠ABE=∠AEB ∴AB=AE ∴AB2=AG·AC
22题:
⑴∵过A(-1,0) B(3,0) 故设y=a(x+1)(x-3) 又过C(0,3)∴a=-1 ∴y=-(x+1)(x-3)=-x2+2x+3①
⑵设PB与y轴交于点D ∵OB=OC ∴∠OCB=∠OBC ∵∠PBC=∠ACB ∴∠ACO=∠DBO
又∠AOC=∠DOB=90°∴OA=OD ∴D(0,-1) ∴yBP=falsex-1② 联合①②解得x=false y=false
∴P(false , false )
⑶∵y=a(x+1)(x-3)=a(x-1)2-4a ∴顶点(1,-4a) 又∵yBC=-x+3 当x=1时yBC=2
∵0<-4a<2 ∴false<a<0
23题:
⑴∵∠C=90°AC=2 BC=2false ∴AB=4 ∴false=false 又 BQ=falseBP ∴false
又∵∠B公共 ∴△BQP∽△BCA ∴∠BQP=∠C=90°即PQ⊥AB
⑵当∠QPD=90°则PD∥AB 又DA=DC ∴BP=PC=false
当∠QDP=90°作QE⊥AC于E 设PB=x,则BQ=BP·cosB=falsex QA=4-falsex
QE=QA·sinA=false(4-falsex)=2false-falsex AE=QA·cosA=false(4-falsex)=2-falsex
∵∠QED=∠QDP=∠DCP=90°∴△QED∽△DCP ∴false
∴false 即3x2-15falsex+52=0 ∴x=false
又∵∠PQD<90°综上BP=false或false
⑶false<BP<false
同课章节目录
