2020--2021学年八年级数学北师大版下册2.4 一元一次不等式(第2课时) 课件(26张)
文档属性
| 名称 | 2020--2021学年八年级数学北师大版下册2.4 一元一次不等式(第2课时) 课件(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 640.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:11:13 | ||
图片预览








文档简介
2.4 一元一次不等式
(第2课时)
北师大版 八年级 数学 下册
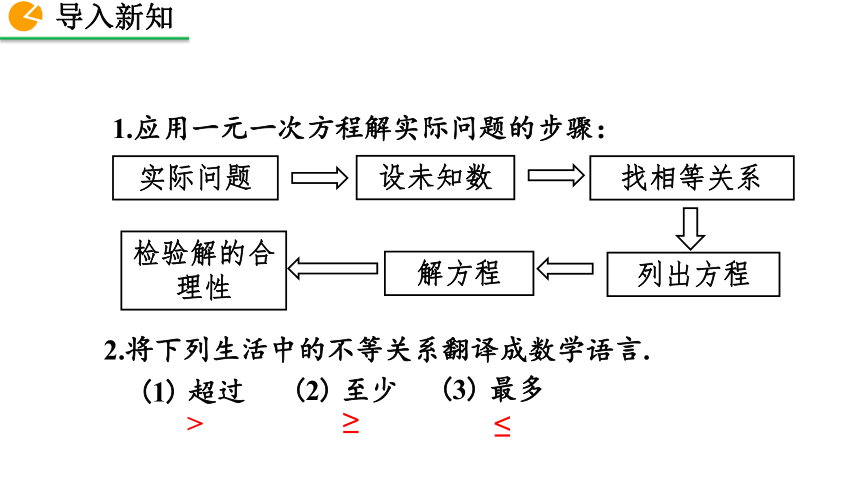
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
导入新知
1.会通过列一元一次不等式去解决生活中的实际问题.
2.体会解不等式过程中的化归思想与类比思想.
素养目标
3.体会分类讨论思想在用不等式解决实际问题中的应用.
探究新知
知识点
一元一次不等式的应用
思考:小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
探究新知
总结:列不等式解应用题的步骤.
(1)审题,找出量与量之间的_________关系;
(2)设未知数;?
(3)列出___________;
(4)解不等式;
(5)根据_________情况,写出答案.?
不等
不等式
实际
探究新知
找不等关系的方法:
(1)直接型的不等关系:可以通过一些___________,如“大于,小于,不大于,不小于,至多,至少,不够,超过”等.?
如“各景点门票都很贵,没有低于100元的”实际上就是_____________100元.?
(2)隐含型的不等关系:不等关系比较隐蔽,表面上没有关键词,需要分析题意,再依据生活实际得出不等关系.
如“保质期6个月”,实际上就是_____________6个月.?
关键词
大于等于
小于等于
探究新知
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
分析:本题涉及的数量关系是:总得分≥85.
一元一次不等式的应用
素养考点 1
探究新知
例1
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2 140元,那么至少购买多少袋面粉?
变式训练
巩固练习
解:(1)设每袋大米x元,每袋面粉y元,
根据题意,得:
答:每袋大米60元,每袋面粉45元.
巩固练习
(2)设购买面粉a袋,则购买大米(40-a)袋,
根据题意,得:60(40-a)+45a≤2 140,
解这个不等式,得:a≥17 ,
∵a为整数,∴最少购买18袋面粉.
解得:
巩固练习
方法总结
在日常生活中,像水费、电费、电话费、出租车收费等问题中,一般出现“至多”“至少”“不超过”“不低于”等关键词语时,便可建立一元一次不等式模型求解.
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
分析: 数量关系: 画册的总重+记事本的总重≤4.5 kg.
变式训练
巩固练习
解:设小明最多只应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
例2 某种服装的进价为240元,出售时标价为360元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打 ( )
A.6折 B.7折 C.8折 D.9折
C
与利润有关的问题
素养考点 2
探究新知
解析:设打了x折,根据题意列不等式得
330×0.1x-240≥240×10%,
解得:x≥8.
B
某商品的标价比成本价高m%,现根据市场需要,该商品需降价n%岀售.为了使获利不低于10%,n应满足 ( )
A.n≤ B.n≤
C.n≤ D.n≤
变式训练
巩固练习
某种商品的进价为320元,为了吸引顾客,按标价的八折出售,这时仍可盈利至少25%,则这种商品的标价最少是________元.
500
变式训练
巩固练习
解析:设这种商品的标价是x元,由题意得:
x×80%-320≥25%×320,
解得:x≥500,
则这种商品的标价最少是500元,
故答案为:500.
连接中考
(2020·宜宾)某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有 ( )
A.2种 B.3种 C.4种 D.5种
B
1.正方形的边长为a cm,它的周长不超过200 cm,则用不等式表示为 ____________.
4a≤200
课堂检测
2.甲种饮料每瓶x元,乙种饮料每瓶(2x-1)元,买3瓶甲
种饮料的钱比买4瓶乙种饮料的钱多:_______________
(列出符合题意的不等式).?
3x>4(2x-1)
基础巩固题
3.小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分钟,跑步的平均速度为210米/分钟,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为 ( )
A.210x+90(15-x)≥1 800 B.90x+210(15-x)≤1 800
C.210x+90(15-x)≥1.8 D.90x+210(15-x)≤1.8
AC=DF
A
课堂检测
基础巩固题
4.小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
解:设她还可能买x支笔,根据题意,得
3 x +2.2×2≤21.
解这个不等式,得 : x ≤ .
因为在这一问题中x只能取正整数,
所以小颖还可能买1支、2支、3支、4支或5支笔.
注意: 问题的实际意义.
课堂检测
基础巩固题
5.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解: 设需要购买x块地板砖,则有
5×4≤0.6×0.6x ,
解得 x ≥ 55.6 ,
由于地板砖的数目必须是整数,所以x的最
小值为56.
答:小明至少要购买56块地板砖.
课堂检测
基础巩固题
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
分析: 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
课堂检测
能力提升题
我市某中学为推进书香校园建设,在全校范围开展图书漂流活动,现需要购进一批甲、乙两种规格的漂流书屋放置图书.已知一个甲种规格的漂流书屋的价格比一个乙种规格的漂流书屋的价格高80元;如果购买2个甲种规格的漂流书屋和3个乙种规格的漂流书屋,一共需要花费960元.
(1)求每个甲种规格的漂流书屋和每个乙种规格的漂流书屋的价格分别是多少元?
(2)如果学校计划购进这两种规格的漂流书屋共15个,并且购买这两种规格的漂流书屋的总费用不超过3 040元,那么该学校至多能购买多少个甲种规格的漂流书屋?
课堂检测
拓广探索题
解:(1)设每个甲种规格的漂流书屋的价格为x元,每个
乙种规格的漂流书屋的价格为y元,
依题意,得:
解得:
答:每个甲种规格的漂流书屋的价格为240元,每个乙种
规格的漂流书屋的价格为160元.
课堂检测
(2)设该学校购买m个甲种规格的漂流书屋,则购买(15-m)个乙种规格的漂流书屋,
依题意,得:240m+160(15-m)≤3 040,
解得:m≤8.
答:该学校至多能购买8个甲种规格的漂流书屋.
课堂检测
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第2课时)
北师大版 八年级 数学 下册
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
导入新知
1.会通过列一元一次不等式去解决生活中的实际问题.
2.体会解不等式过程中的化归思想与类比思想.
素养目标
3.体会分类讨论思想在用不等式解决实际问题中的应用.
探究新知
知识点
一元一次不等式的应用
思考:小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
探究新知
总结:列不等式解应用题的步骤.
(1)审题,找出量与量之间的_________关系;
(2)设未知数;?
(3)列出___________;
(4)解不等式;
(5)根据_________情况,写出答案.?
不等
不等式
实际
探究新知
找不等关系的方法:
(1)直接型的不等关系:可以通过一些___________,如“大于,小于,不大于,不小于,至多,至少,不够,超过”等.?
如“各景点门票都很贵,没有低于100元的”实际上就是_____________100元.?
(2)隐含型的不等关系:不等关系比较隐蔽,表面上没有关键词,需要分析题意,再依据生活实际得出不等关系.
如“保质期6个月”,实际上就是_____________6个月.?
关键词
大于等于
小于等于
探究新知
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
分析:本题涉及的数量关系是:总得分≥85.
一元一次不等式的应用
素养考点 1
探究新知
例1
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2 140元,那么至少购买多少袋面粉?
变式训练
巩固练习
解:(1)设每袋大米x元,每袋面粉y元,
根据题意,得:
答:每袋大米60元,每袋面粉45元.
巩固练习
(2)设购买面粉a袋,则购买大米(40-a)袋,
根据题意,得:60(40-a)+45a≤2 140,
解这个不等式,得:a≥17 ,
∵a为整数,∴最少购买18袋面粉.
解得:
巩固练习
方法总结
在日常生活中,像水费、电费、电话费、出租车收费等问题中,一般出现“至多”“至少”“不超过”“不低于”等关键词语时,便可建立一元一次不等式模型求解.
当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本各重1.2 kg的画册和一批每本重0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
分析: 数量关系: 画册的总重+记事本的总重≤4.5 kg.
变式训练
巩固练习
解:设小明最多只应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
由于记事本的数目必须是整数,所以x 的最大值为5.
例2 某种服装的进价为240元,出售时标价为360元,由于换季,商店准备打折销售,但要保持利润不低于20%,那么至多打 ( )
A.6折 B.7折 C.8折 D.9折
C
与利润有关的问题
素养考点 2
探究新知
解析:设打了x折,根据题意列不等式得
330×0.1x-240≥240×10%,
解得:x≥8.
B
某商品的标价比成本价高m%,现根据市场需要,该商品需降价n%岀售.为了使获利不低于10%,n应满足 ( )
A.n≤ B.n≤
C.n≤ D.n≤
变式训练
巩固练习
某种商品的进价为320元,为了吸引顾客,按标价的八折出售,这时仍可盈利至少25%,则这种商品的标价最少是________元.
500
变式训练
巩固练习
解析:设这种商品的标价是x元,由题意得:
x×80%-320≥25%×320,
解得:x≥500,
则这种商品的标价最少是500元,
故答案为:500.
连接中考
(2020·宜宾)某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有 ( )
A.2种 B.3种 C.4种 D.5种
B
1.正方形的边长为a cm,它的周长不超过200 cm,则用不等式表示为 ____________.
4a≤200
课堂检测
2.甲种饮料每瓶x元,乙种饮料每瓶(2x-1)元,买3瓶甲
种饮料的钱比买4瓶乙种饮料的钱多:_______________
(列出符合题意的不等式).?
3x>4(2x-1)
基础巩固题
3.小明要从甲地到乙地,两地相距1.8千米.已知他步行的平均速度为90米/分钟,跑步的平均速度为210米/分钟,若他要在不超过15分钟的时间内从甲地到达乙地,至少需要跑步多少分钟?设他需要跑步x分钟,则列出的不等式为 ( )
A.210x+90(15-x)≥1 800 B.90x+210(15-x)≤1 800
C.210x+90(15-x)≥1.8 D.90x+210(15-x)≤1.8
AC=DF
A
课堂检测
基础巩固题
4.小颖准备用21元钱买笔和笔记本.已知每支笔3元,每个笔记本2.2元,她买了2个笔记本.请你帮她算一算,她还可能买几支笔?
解:设她还可能买x支笔,根据题意,得
3 x +2.2×2≤21.
解这个不等式,得 : x ≤ .
因为在这一问题中x只能取正整数,
所以小颖还可能买1支、2支、3支、4支或5支笔.
注意: 问题的实际意义.
课堂检测
基础巩固题
5.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解: 设需要购买x块地板砖,则有
5×4≤0.6×0.6x ,
解得 x ≥ 55.6 ,
由于地板砖的数目必须是整数,所以x的最
小值为56.
答:小明至少要购买56块地板砖.
课堂检测
基础巩固题
某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10%≥900.
解得
x ≥ 125.
答:每套童装的售价至少是125元.
分析: 本题涉及的数量关系是:
销售额-成本-税费≥纯利润(900元).
课堂检测
能力提升题
我市某中学为推进书香校园建设,在全校范围开展图书漂流活动,现需要购进一批甲、乙两种规格的漂流书屋放置图书.已知一个甲种规格的漂流书屋的价格比一个乙种规格的漂流书屋的价格高80元;如果购买2个甲种规格的漂流书屋和3个乙种规格的漂流书屋,一共需要花费960元.
(1)求每个甲种规格的漂流书屋和每个乙种规格的漂流书屋的价格分别是多少元?
(2)如果学校计划购进这两种规格的漂流书屋共15个,并且购买这两种规格的漂流书屋的总费用不超过3 040元,那么该学校至多能购买多少个甲种规格的漂流书屋?
课堂检测
拓广探索题
解:(1)设每个甲种规格的漂流书屋的价格为x元,每个
乙种规格的漂流书屋的价格为y元,
依题意,得:
解得:
答:每个甲种规格的漂流书屋的价格为240元,每个乙种
规格的漂流书屋的价格为160元.
课堂检测
(2)设该学校购买m个甲种规格的漂流书屋,则购买(15-m)个乙种规格的漂流书屋,
依题意,得:240m+160(15-m)≤3 040,
解得:m≤8.
答:该学校至多能购买8个甲种规格的漂流书屋.
课堂检测
一元一次不等式的应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
