2020--2021学年八年级数学北师大版下册第二章2.4 一元一次不等式(第1课时)课件(25张)
文档属性
| 名称 | 2020--2021学年八年级数学北师大版下册第二章2.4 一元一次不等式(第1课时)课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:14:08 | ||
图片预览







文档简介
2.4 一元一次不等式
(第1课时)
北师大版 八年级 数学 下册
1.什么叫一元一次方程 ?
“只含一个未知数、并且未知数的指数是1”
的整式方程.
2.不等式的基本性质:
不等式性质1:不等式的两边都加(或减)同一个整式,不等号的方向不变.
不等式性质2:不等式两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
导入新知
1.理解和掌握一元一次不等式的概念.
2.会用不等式的性质熟练地解一元一次不等式,并能在数轴上表示其解集.
素养目标
每个不等式都只含有一个未知数;并且未知数的次数是1;不等号的两边都是整式.
知识点 1
一元一次不等式的概念
探究新知
观察下列不等式:
(1)6+3x>30 (2)x+17<5x (3)x>5 (4)
这些不等式有哪些共同点?
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
结论
探究新知
(1)是用不等号连接的式子;
(2)两边都是整式;
(3)含有一个未知数;
(4)未知数最高次数为1且其系数不为0.
一元一次不等式必须同时满足的“四个条件”:
识别一元一次不等式
素养考点 1
探究新知
C
例 下列不等式中,一元一次不等式有( )
(1)3x>-9. (2)3(x+2)-4x(3) + (x-1)≥1. (4) -5≤ .
A.1个 B.2个 C.3个 D.4个
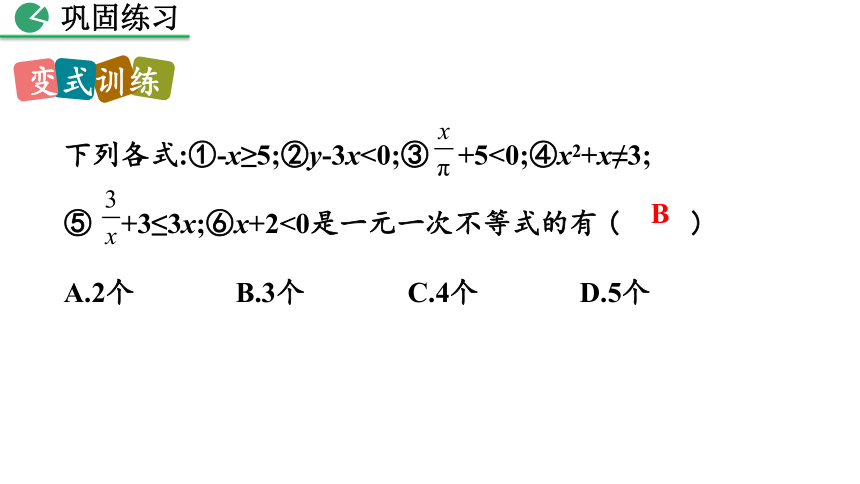
下列各式:①-x≥5;②y-3x<0;③ +5<0;④x2+x≠3;
⑤ +3≤3x;⑥x+2<0是一元一次不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
B
变式训练
巩固练习
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
探究新知
解一元一次不等式
知识点 2
去分母 去括号 移项 合并同类项
等式两边同除以未知数的系数.
解一元一次方程的步骤:
解一元一次方程的依据是等式的两个性质.
解一元一次方程时,它的移项法则是:
等号不变 , 把一项从等式的一边移到另一边后要改变符号.
等式的基本性质是:
等式的两边同时加(或减)同一个数,等式仍然成立.
等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立.
探究新知
去分母 去括号 移项 合并同类项
不等式两边同除以未知数的系数.
不等号不变 , 把一项从不等式的一边移到另一边后要改变符号.
解一元一次不等式的步骤:
解一元一次不等式的依据是 .
解一元一次不等式时,它的移项法则是:
不等式的基本性质是:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
不等式的三个性质
不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
讲授新课
探究新知
解一元一次不等式的注意事项:
(2)要注意区分“大于”、“不大于”、“小于”、“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确的表达出来.
(3)在数轴上表示解集应注意的问题:
方向、空心或实心.
(1)在运用性质3时要特别注意:
不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
探究新知
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为xa的形式.
探究新知
归纳总结
讲授新课
解一元一次不等式
素养考点 2
探究新知
解:
两边都加上x,得
-3 -2 -1 0 1 2 3 4
合并同类项,得
两边都加上–6,得
合并同类项,得
两边都除以3,得
即
这个不等式的解集在
数轴上表示如下:
解不等式3–x<2x+6,并把它的解集表示在数轴上.
例1
解:去分母得3(x-2) ≥ 2(7-x),
去括号得3x-6 ≥ 14-2x,
移项、合并同类项得5x ≥ 20,
系数化为1,得x ≥ 4.
探究新知
解不等式 ≥ ,并把它的解集表示在数轴上.
例2
这里改为“并把它的解集表示在数轴上”,答案增加解集的数轴表示
-1
0
1
2
3
4
5
6
在数轴上表示如图:
方法总结
解一元一次不等式的四点注意
(1)去分母:去分母时要注意每一项都要乘以分母的最小公倍数.不要漏乘不含分母的项.
(2)去括号:根据乘法的分配律不要漏乘项.
(3)移项:移项要注意改变该项的符号,不等号方向不变.
(4)系数化为1:两边都除以负数时注意不等号方向要改变.
探究新知
解不等式:3x-1≥2(x-1),并把它的解集在数轴上表示出来.
巩固练习
变式训练
解:3x-1≥2(x-1),
去括号得3x-1≥2x-2,?
移项得3x-2x≥-2+1,?
合并同类项得x≥-1 . ?
在数轴上表示如图:
连接中考
(2020?天水)若关于x的不等式3x+a≤2只有2个正整数解,则a的取值范围为( )
A.-7<a<-4 B.-7≤a ≤ -4
C. -7 ≤ a<-4 D. -7<a ≤ -4
D
A
1.下列不等式是一元一次不等式的是( )
A.x>3 B.x+ <0
C.x+y>0 D.x2+x+9≥0
课堂检测
基础巩固题
2.不等式2x-3>-5的解集在数轴上表示正确的是 ( )
C
课堂检测
基础巩固题
3. 不等式2(1-x)-4<0的解集是_______.?
x>-1
C
4.若3m-5x3+m>4是关于x的一元一次不等式,则该不等式的解集是( )
A.x< B.x>
C.x<-2 D.x>-2
课堂检测
基础巩固题
1、若(m+1)x|m|+2>0是关于x的一元一次不等式,则m=______.?
1
2、已知 (m+4)x|m|-3+6>0是关于x的一元一次不等式,则m的值为( )
A.4 B.±4 C.3 D.±3
A
课堂检测
能力提升题
3、解不等式 ≥ -2,并把它的解集表示在数轴上.?
解:去分母,得3(2+x)≥2(2x-1)-12,
去括号,得6+3x≥4x-2-12,
移项,得3x-4x≥-2-12-6,
合并同类项,得-x≥-20,
系数化为1,得x≤20.
课堂检测
0
10
20
能力提升题
已知关于x的方程组
的解满足x+y>0,求k的取值范围.
解:(1)+(2)得
∵ x+y>0,
课堂检测
拓广探索题
一元一次不等式的概念和
解法
一元一次不等式的概念
解一元一次不等式的步骤
课堂小结
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
去分母 去括号 移项
合并同类项 不等式
两边同除以未知数的系数.
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第1课时)
北师大版 八年级 数学 下册
1.什么叫一元一次方程 ?
“只含一个未知数、并且未知数的指数是1”
的整式方程.
2.不等式的基本性质:
不等式性质1:不等式的两边都加(或减)同一个整式,不等号的方向不变.
不等式性质2:不等式两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
导入新知
1.理解和掌握一元一次不等式的概念.
2.会用不等式的性质熟练地解一元一次不等式,并能在数轴上表示其解集.
素养目标
每个不等式都只含有一个未知数;并且未知数的次数是1;不等号的两边都是整式.
知识点 1
一元一次不等式的概念
探究新知
观察下列不等式:
(1)6+3x>30 (2)x+17<5x (3)x>5 (4)
这些不等式有哪些共同点?
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
结论
探究新知
(1)是用不等号连接的式子;
(2)两边都是整式;
(3)含有一个未知数;
(4)未知数最高次数为1且其系数不为0.
一元一次不等式必须同时满足的“四个条件”:
识别一元一次不等式
素养考点 1
探究新知
C
例 下列不等式中,一元一次不等式有( )
(1)3x>-9. (2)3(x+2)-4x
A.1个 B.2个 C.3个 D.4个
下列各式:①-x≥5;②y-3x<0;③ +5<0;④x2+x≠3;
⑤ +3≤3x;⑥x+2<0是一元一次不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
B
变式训练
巩固练习
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
探究新知
解一元一次不等式
知识点 2
去分母 去括号 移项 合并同类项
等式两边同除以未知数的系数.
解一元一次方程的步骤:
解一元一次方程的依据是等式的两个性质.
解一元一次方程时,它的移项法则是:
等号不变 , 把一项从等式的一边移到另一边后要改变符号.
等式的基本性质是:
等式的两边同时加(或减)同一个数,等式仍然成立.
等式的两边同时乘(或除以)同一个数(0除外),等式仍然成立.
探究新知
去分母 去括号 移项 合并同类项
不等式两边同除以未知数的系数.
不等号不变 , 把一项从不等式的一边移到另一边后要改变符号.
解一元一次不等式的步骤:
解一元一次不等式的依据是 .
解一元一次不等式时,它的移项法则是:
不等式的基本性质是:
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
不等式的三个性质
不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
讲授新课
探究新知
解一元一次不等式的注意事项:
(2)要注意区分“大于”、“不大于”、“小于”、“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确的表达出来.
(3)在数轴上表示解集应注意的问题:
方向、空心或实心.
(1)在运用性质3时要特别注意:
不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
探究新知
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x
探究新知
归纳总结
讲授新课
解一元一次不等式
素养考点 2
探究新知
解:
两边都加上x,得
-3 -2 -1 0 1 2 3 4
合并同类项,得
两边都加上–6,得
合并同类项,得
两边都除以3,得
即
这个不等式的解集在
数轴上表示如下:
解不等式3–x<2x+6,并把它的解集表示在数轴上.
例1
解:去分母得3(x-2) ≥ 2(7-x),
去括号得3x-6 ≥ 14-2x,
移项、合并同类项得5x ≥ 20,
系数化为1,得x ≥ 4.
探究新知
解不等式 ≥ ,并把它的解集表示在数轴上.
例2
这里改为“并把它的解集表示在数轴上”,答案增加解集的数轴表示
-1
0
1
2
3
4
5
6
在数轴上表示如图:
方法总结
解一元一次不等式的四点注意
(1)去分母:去分母时要注意每一项都要乘以分母的最小公倍数.不要漏乘不含分母的项.
(2)去括号:根据乘法的分配律不要漏乘项.
(3)移项:移项要注意改变该项的符号,不等号方向不变.
(4)系数化为1:两边都除以负数时注意不等号方向要改变.
探究新知
解不等式:3x-1≥2(x-1),并把它的解集在数轴上表示出来.
巩固练习
变式训练
解:3x-1≥2(x-1),
去括号得3x-1≥2x-2,?
移项得3x-2x≥-2+1,?
合并同类项得x≥-1 . ?
在数轴上表示如图:
连接中考
(2020?天水)若关于x的不等式3x+a≤2只有2个正整数解,则a的取值范围为( )
A.-7<a<-4 B.-7≤a ≤ -4
C. -7 ≤ a<-4 D. -7<a ≤ -4
D
A
1.下列不等式是一元一次不等式的是( )
A.x>3 B.x+ <0
C.x+y>0 D.x2+x+9≥0
课堂检测
基础巩固题
2.不等式2x-3>-5的解集在数轴上表示正确的是 ( )
C
课堂检测
基础巩固题
3. 不等式2(1-x)-4<0的解集是_______.?
x>-1
C
4.若3m-5x3+m>4是关于x的一元一次不等式,则该不等式的解集是( )
A.x< B.x>
C.x<-2 D.x>-2
课堂检测
基础巩固题
1、若(m+1)x|m|+2>0是关于x的一元一次不等式,则m=______.?
1
2、已知 (m+4)x|m|-3+6>0是关于x的一元一次不等式,则m的值为( )
A.4 B.±4 C.3 D.±3
A
课堂检测
能力提升题
3、解不等式 ≥ -2,并把它的解集表示在数轴上.?
解:去分母,得3(2+x)≥2(2x-1)-12,
去括号,得6+3x≥4x-2-12,
移项,得3x-4x≥-2-12-6,
合并同类项,得-x≥-20,
系数化为1,得x≤20.
课堂检测
0
10
20
能力提升题
已知关于x的方程组
的解满足x+y>0,求k的取值范围.
解:(1)+(2)得
∵ x+y>0,
课堂检测
拓广探索题
一元一次不等式的概念和
解法
一元一次不等式的概念
解一元一次不等式的步骤
课堂小结
只含一个未知数,并且未知数的最高次数是1,不等式的左右两边都是整式,像这样的不等式,叫做一元一次不等式.
去分母 去括号 移项
合并同类项 不等式
两边同除以未知数的系数.
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
