2020--2021学年八年级数学北师大版下册第二章2.5 一元一次不等式与一次函数(第1课时) 课件(28张)
文档属性
| 名称 | 2020--2021学年八年级数学北师大版下册第二章2.5 一元一次不等式与一次函数(第1课时) 课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 526.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:14:57 | ||
图片预览






文档简介
2.5 一元一次不等式
与一次函数
(第1课时)
北师大版 八年级 数学 下册
2.一次函数y=ax+b(a≠0)的图象是__________.它与x轴的交点坐标是 ,与y轴的交点坐标是 ;要作一次函数的图象,只需_______点即可.
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 .
一条直线
(0,b)
两
(0,-5)
1.解不等式2x-5>0.
下面我们来探讨一下一元一次不等式与一次函数之间的关系.
导入新知
1.体会一元一次不等式与一次函数的内在联系.
2.利用不等式与函数的关系解决简单的实际问题.
素养目标
3.通过作函数图像,观察函数图像初步体验数形结合思想.
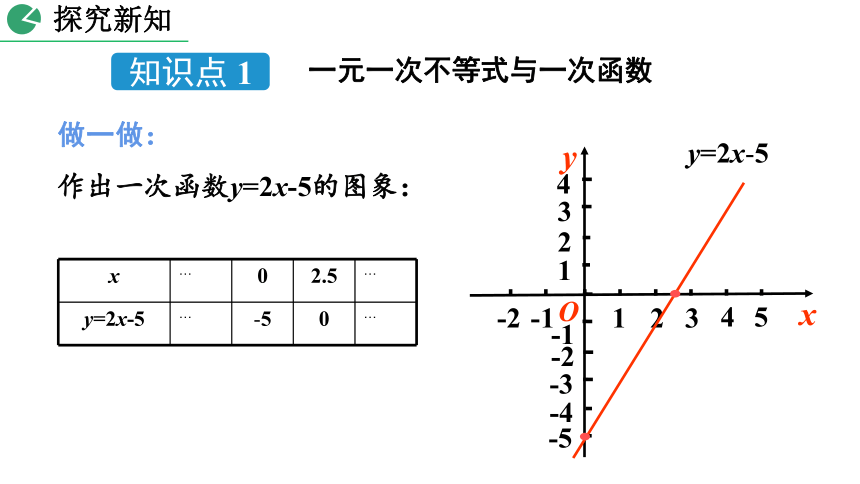
做一做:
作出一次函数y=2x-5的图象:
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
x
…
0
2.5
…
y=2x-5
…
-5
0
…
探究新知
知识点 1
一元一次不等式与一次函数
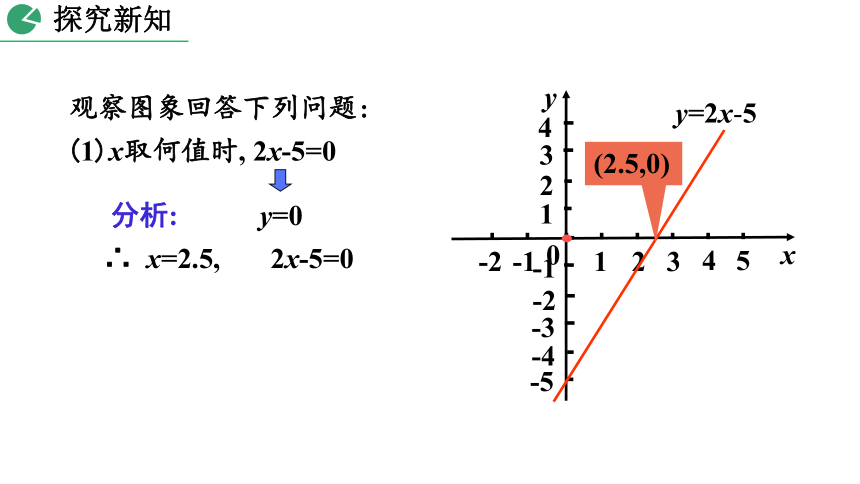
观察图象回答下列问题:
(1)x取何值时, 2x-5=0
∴ x=2.5, 2x-5=0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y=0
探究新知
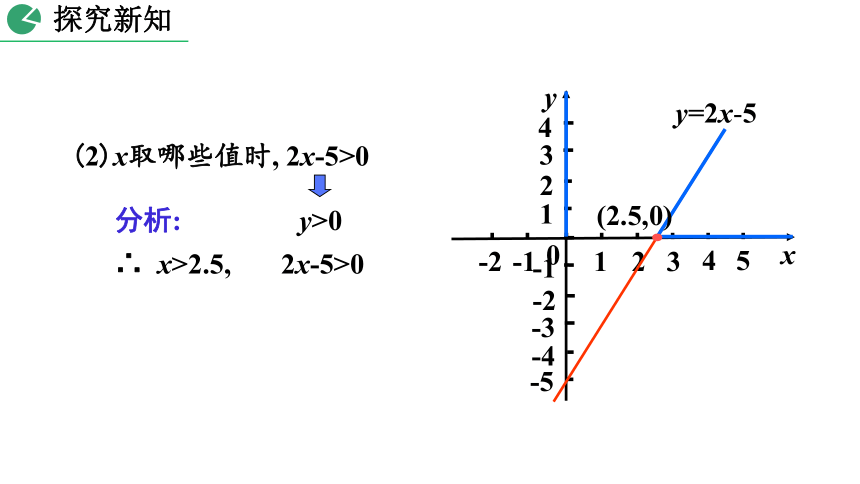
(2)x取哪些值时, 2x-5>0
∴ x>2.5, 2x-5>0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y>0
探究新知
(3)x取哪些值时, 2x-5<0
∴ x<2.5, 2x-5<0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y<0
探究新知
(4)x取哪些值时, 2x-5>3
∴ x>4, 2x-5>3
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
分析:
y=3
探究新知
由上述讨论易知:
“关于一次函数的值的问题” 可变换成 “关于一元一次不等式的问题” ;
反过来,“关于一元一次不等式的问题”可变换成 “关于一次函数的值的问题”.
因此,我们既可以运用函数图象解不等式 ,也可以运用解不等式帮助研究函数问题 ,二者相互渗透 ,互相作用.
不等式与函数 、方程是紧密联系着的一个整体 .
探究新知
想一想:如果y=-2x-5,那么当x取何值时, y>0?
0
-3
-2
-1
1
2
-5
-4
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=-2x-5
思路二:
将函数问题转化为不等式问题.
即 解不等式-2x-5 >0
∴当x<-2.5时, y>0.
思路一:
运用函数图象解不等式.
由图象可得
当x<-2.5时, y>0.
(-2.5,0)
作一次函数y=-2x-5的图象
探究新知
一元一次不等式与一次函数之间的关系
一次函数与一元一次方程、一元一次不等式之间有紧
密联系,当函数值等于0时,即为_____________;当函数值大
于或小于0时,即为______________.?
一元一次方程
一元一次不等式
总结:
探究新知
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方(或
下方)时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
探究新知
如图所示是函数y=- x+3的图象,那么方程
- x+3=0的解是________,不等式- x+3<0的解集是
________,当y>3时,x的取值范围是________.?
x=4
x>4
x<0
巩固练习
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自已才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
(4)你是怎样求解的?与同伴交流.
解:设哥哥起跑后所用的时间为x(s). 哥哥跑过的距离为y1(m),弟弟跑过的距离为y2(m).则哥哥与弟弟每人所跑的距离y(m)与时间x(s)之间的函数关系式分别是:
y1=4x
y2=3x+9
探究新知
知识点2
用一次函数图像解一元一次不等式ax +b> cx +d(或ax +b< cx +d)
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
(3)______先跑过20m.______先跑过100m.
方法一:图象法
0(s)x>9(s)
y1=4x
y2=3x+9
(9,36)
0
6
8
10
2
x(s)
4
12
24
12
30
18
36
6
y(m)
42
48
弟弟
哥哥
探究新知
方法二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
4x<3x+9
x<9
4x>3x+9
x>9
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m
∴哥哥先跑过100m
探究新知
因此,当 时,y1>y2.
已知y1=-x+3, y2=3x-4,当x取何值时y1>y2你是怎样做的?与同伴交流.
解法2:根据题意,得
-x+3> 3x-4,
解得
巩固练习
当 时,y1>y2.
解法1:观察图象可知,
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y2=3x-4
y1=-x+3
方法总结
对于两个一次函数y1=k1x+b1(k1≠0)和y2=k2x+b2(k2≠0),
若比较y1与y2的大小,即是比较k1x+b1与k2x+b2的大小,
即为求不等式k1x+b1>k2x+b2(或k1x+b1巩固练习
(2020?湘潭)如图,直线y=kx+b(k<0)经过点p(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1
C.x<1 D.x>1
连接中考
A
C
2. 如图,直线y=ax+b(a≠0)过点A,B,则不等式ax+b>0的解集是 ( )
A.x>4 B.x>0
C.x>-3 D.x>
课堂检测
基础巩固题
1.在一次函数y=-2x+8中,若y>0,则 ( )
A.x>4 B.x<4 C.x>0 D.x<0
B
4.如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b< x时,x的取值范围为________.?
x>3
课堂检测
3.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式
x-2≥-x+2的解集是_________.?
x≥2
基础巩固题
5.如图,直线l1:y1=2x+1与直线l2:y2=mx+4相交于点P(1,b).
(1)求b和m的值.
(2)结合图象,直接写出当y1>y2时x的取值范围.
课堂检测
基础巩固题
解:(1)对于直线y1=2x+1,当x=1时,y1=3,
∴P(1,3),b=3,
把P(1,3)代入y2=mx+4中,得3=m+4,
解得m=-1.
(2)观察图象可知:当y1>y2时x的取值范围是x>1.
-2
x
y=3x+6
y
1、根据下列一次函数的图像,直接写出下列不等式的解集.
x
y
3
y=-x+3
x>-2
x≤3
x≤-2
x>3
(1)3x+6>0
(即y>0)
(2)3x+6 ≤0
(即y≤0)
(4) –x+3<0
(即y<0)
(3) –x+3 ≥0
(即y≥0)
课堂检测
能力提升题
y
2.利用y= 的图像,
直接写出:
2
5
x
y= x+5
x=2
x<2
x>2
x<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
课堂检测
能力提升题
(1)方程 的解
(2)不等式 的解集
(3)不等式 的解集
(4)不等式 的解集
甲、乙两辆摩托车从相距20km的A、B两地相向而行,图中l1、l2分别表示两辆摩托车离A地的距离s(km)
与行驶时间t(h)之间函数关系.
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A、B两地
中点?
课堂检测
拓广探索题
解:(1)从图象中可知
故摩托车乙速度快.
(2)当s=10km时,
即经过0.3h时,甲车行驶到A、B两地的中点.
课堂检测
一元一次不等式
一次函数
可以研究一次函数的图象走向
通过图象可直接解不等式
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
与一次函数
(第1课时)
北师大版 八年级 数学 下册
2.一次函数y=ax+b(a≠0)的图象是__________.它与x轴的交点坐标是 ,与y轴的交点坐标是 ;要作一次函数的图象,只需_______点即可.
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 .
一条直线
(0,b)
两
(0,-5)
1.解不等式2x-5>0.
下面我们来探讨一下一元一次不等式与一次函数之间的关系.
导入新知
1.体会一元一次不等式与一次函数的内在联系.
2.利用不等式与函数的关系解决简单的实际问题.
素养目标
3.通过作函数图像,观察函数图像初步体验数形结合思想.
做一做:
作出一次函数y=2x-5的图象:
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
x
…
0
2.5
…
y=2x-5
…
-5
0
…
探究新知
知识点 1
一元一次不等式与一次函数
观察图象回答下列问题:
(1)x取何值时, 2x-5=0
∴ x=2.5, 2x-5=0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y=0
探究新知
(2)x取哪些值时, 2x-5>0
∴ x>2.5, 2x-5>0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y>0
探究新知
(3)x取哪些值时, 2x-5<0
∴ x<2.5, 2x-5<0
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
(2.5,0)
分析:
y<0
探究新知
(4)x取哪些值时, 2x-5>3
∴ x>4, 2x-5>3
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=2x-5
分析:
y=3
探究新知
由上述讨论易知:
“关于一次函数的值的问题” 可变换成 “关于一元一次不等式的问题” ;
反过来,“关于一元一次不等式的问题”可变换成 “关于一次函数的值的问题”.
因此,我们既可以运用函数图象解不等式 ,也可以运用解不等式帮助研究函数问题 ,二者相互渗透 ,互相作用.
不等式与函数 、方程是紧密联系着的一个整体 .
探究新知
想一想:如果y=-2x-5,那么当x取何值时, y>0?
0
-3
-2
-1
1
2
-5
-4
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=-2x-5
思路二:
将函数问题转化为不等式问题.
即 解不等式-2x-5 >0
∴当x<-2.5时, y>0.
思路一:
运用函数图象解不等式.
由图象可得
当x<-2.5时, y>0.
(-2.5,0)
作一次函数y=-2x-5的图象
探究新知
一元一次不等式与一次函数之间的关系
一次函数与一元一次方程、一元一次不等式之间有紧
密联系,当函数值等于0时,即为_____________;当函数值大
于或小于0时,即为______________.?
一元一次方程
一元一次不等式
总结:
探究新知
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
函数y= ax+b的函数值
大于0(或小于0)时x
的取值范围
直线y= ax+b在x轴上方(或
下方)时自变量的取值范围
从数的角度看
从形的角度看
求ax+b>0(或<0)(a, b
是常数,a≠0)的解集
探究新知
如图所示是函数y=- x+3的图象,那么方程
- x+3=0的解是________,不等式- x+3<0的解集是
________,当y>3时,x的取值范围是________.?
x=4
x>4
x<0
巩固练习
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自已才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
(4)你是怎样求解的?与同伴交流.
解:设哥哥起跑后所用的时间为x(s). 哥哥跑过的距离为y1(m),弟弟跑过的距离为y2(m).则哥哥与弟弟每人所跑的距离y(m)与时间x(s)之间的函数关系式分别是:
y1=4x
y2=3x+9
探究新知
知识点2
用一次函数图像解一元一次不等式ax +b> cx +d(或ax +b< cx +d)
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
(3)______先跑过20m.______先跑过100m.
方法一:图象法
0(s)
y1=4x
y2=3x+9
(9,36)
0
6
8
10
2
x(s)
4
12
24
12
30
18
36
6
y(m)
42
48
弟弟
哥哥
探究新知
方法二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过100m?
4x<3x+9
x<9
4x>3x+9
x>9
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m
∴哥哥先跑过100m
探究新知
因此,当 时,y1>y2.
已知y1=-x+3, y2=3x-4,当x取何值时y1>y2你是怎样做的?与同伴交流.
解法2:根据题意,得
-x+3> 3x-4,
解得
巩固练习
当 时,y1>y2.
解法1:观察图象可知,
0
1
2
3
4
5
-2
-1
x
2
-1
3
1
4
-3
-5
-2
-4
y
y2=3x-4
y1=-x+3
方法总结
对于两个一次函数y1=k1x+b1(k1≠0)和y2=k2x+b2(k2≠0),
若比较y1与y2的大小,即是比较k1x+b1与k2x+b2的大小,
即为求不等式k1x+b1>k2x+b2(或k1x+b1
(2020?湘潭)如图,直线y=kx+b(k<0)经过点p(1,1),当kx+b≥x时,则x的取值范围为( )
A.x≤1 B.x≥1
C.x<1 D.x>1
连接中考
A
C
2. 如图,直线y=ax+b(a≠0)过点A,B,则不等式ax+b>0的解集是 ( )
A.x>4 B.x>0
C.x>-3 D.x>
课堂检测
基础巩固题
1.在一次函数y=-2x+8中,若y>0,则 ( )
A.x>4 B.x<4 C.x>0 D.x<0
B
4.如图,直线y=kx+b(k<0)经过点A(3,1),当kx+b< x时,x的取值范围为________.?
x>3
课堂检测
3.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式
x-2≥-x+2的解集是_________.?
x≥2
基础巩固题
5.如图,直线l1:y1=2x+1与直线l2:y2=mx+4相交于点P(1,b).
(1)求b和m的值.
(2)结合图象,直接写出当y1>y2时x的取值范围.
课堂检测
基础巩固题
解:(1)对于直线y1=2x+1,当x=1时,y1=3,
∴P(1,3),b=3,
把P(1,3)代入y2=mx+4中,得3=m+4,
解得m=-1.
(2)观察图象可知:当y1>y2时x的取值范围是x>1.
-2
x
y=3x+6
y
1、根据下列一次函数的图像,直接写出下列不等式的解集.
x
y
3
y=-x+3
x>-2
x≤3
x≤-2
x>3
(1)3x+6>0
(即y>0)
(2)3x+6 ≤0
(即y≤0)
(4) –x+3<0
(即y<0)
(3) –x+3 ≥0
(即y≥0)
课堂检测
能力提升题
y
2.利用y= 的图像,
直接写出:
2
5
x
y= x+5
x=2
x<2
x>2
x<0
(即y=0)
(即y>0)
(即y<0)
(即y>5)
课堂检测
能力提升题
(1)方程 的解
(2)不等式 的解集
(3)不等式 的解集
(4)不等式 的解集
甲、乙两辆摩托车从相距20km的A、B两地相向而行,图中l1、l2分别表示两辆摩托车离A地的距离s(km)
与行驶时间t(h)之间函数关系.
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A、B两地
中点?
课堂检测
拓广探索题
解:(1)从图象中可知
故摩托车乙速度快.
(2)当s=10km时,
即经过0.3h时,甲车行驶到A、B两地的中点.
课堂检测
一元一次不等式
一次函数
可以研究一次函数的图象走向
通过图象可直接解不等式
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
