2020-2021学年湘教版(2012)初中数学八年级下册 1.4 角平分线的性质 课件(25张)
文档属性
| 名称 | 2020-2021学年湘教版(2012)初中数学八年级下册 1.4 角平分线的性质 课件(25张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览



文档简介
角是轴对称图形吗?如果是,它的对称轴是什么?
角平分线的概念
一条射线 将 一个角 分成为两个相等的角,这条射线就叫做这个角的角平分线。
回顾与思考
角平分线的性质
复习回顾:
1)什么是点到直线的距离?
②直线外一点到直线上的所有点的连线中,
垂线段的长度,叫做点到直线的距离
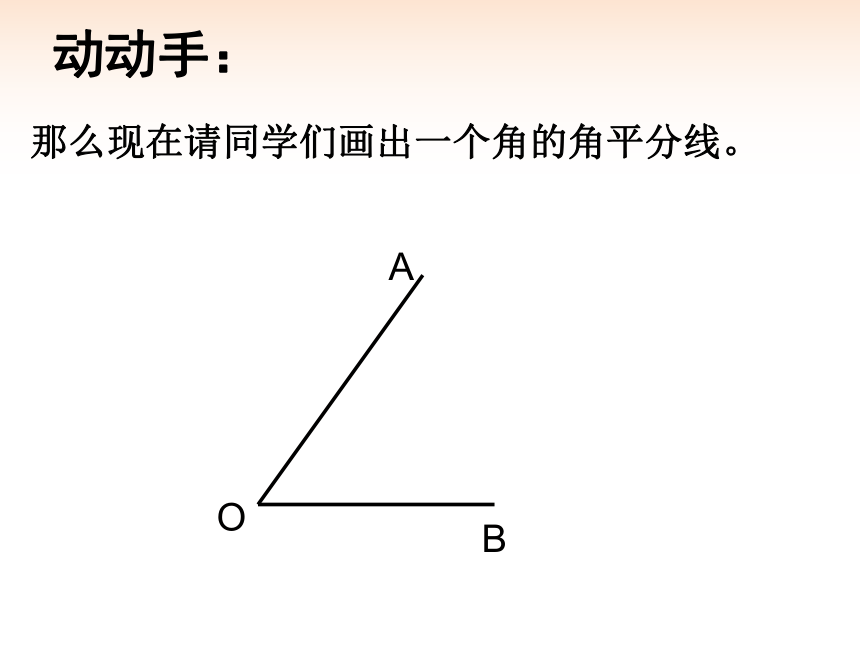
动动手:
那么现在请同学们画出一个角的角平分线。
A
O
B
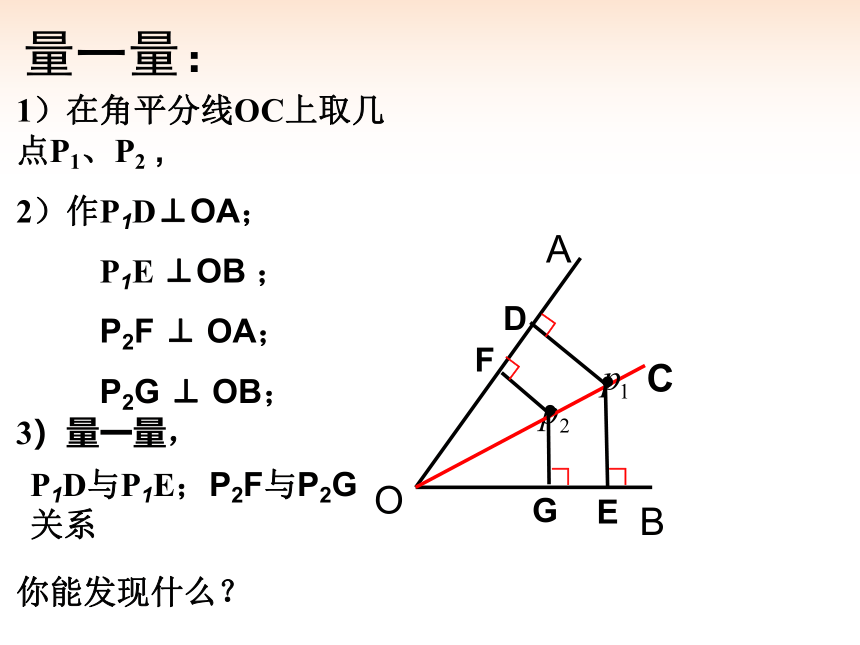
量一量:
A
O
B
C
1)在角平分线OC上取几点P1、P2 ,
2)作P1D⊥OA;
P1E ⊥OB ;
P2F ⊥ OA;
P2G ⊥ OB;
3)量一量,
你能发现什么?
P1D与P1E;P2F与P2G关系
●
●
E
G
F
D
?
?
?
?
A
B
O
P
D
E
3
4
C
1
2
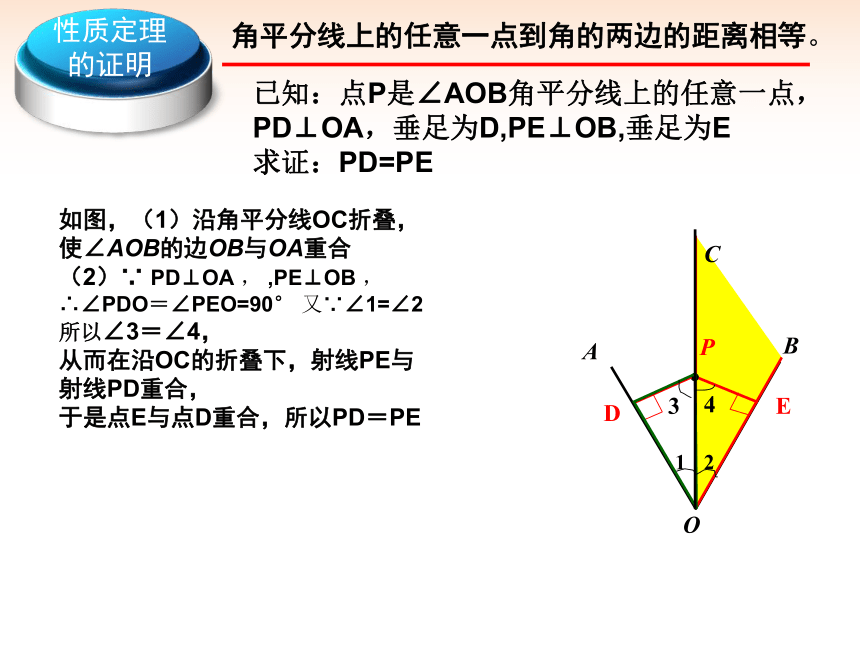
如图,(1)沿角平分线OC折叠,使∠AOB的边OB与OA重合
(2)∵ PD⊥OA , ,PE⊥OB , ∴∠PDO=∠PEO=90° 又∵∠1=∠2所以∠3=∠4,
从而在沿OC的折叠下,射线PE与射线PD重合,
于是点E与点D重合,所以PD=PE
已知:点P是∠AOB角平分线上的任意一点, PD⊥OA,垂足为D,PE⊥OB,垂足为E
求证:PD=PE
性质定理的证明
角平分线上的任意一点到角的两边的距离相等。
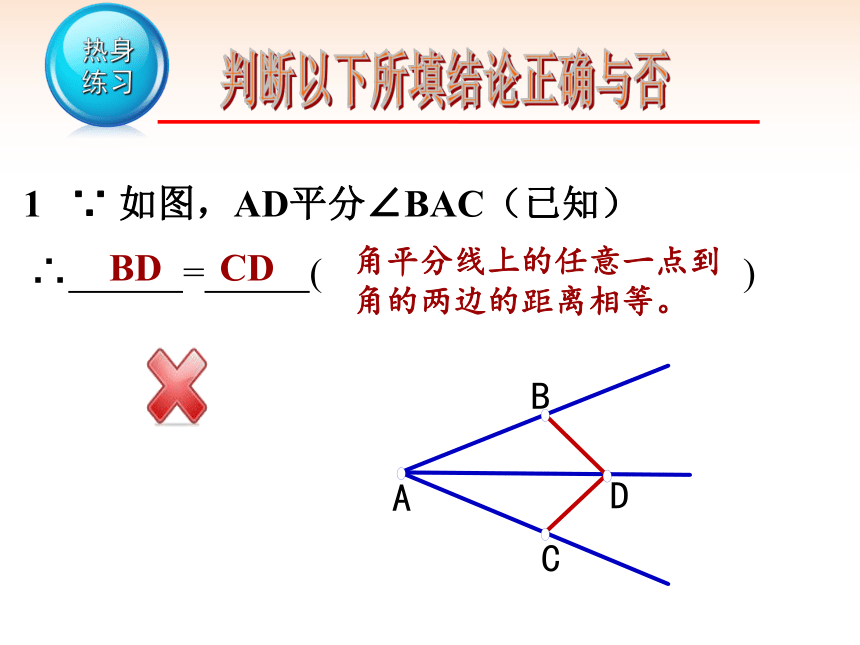
1 ∵ 如图,AD平分∠BAC(已知)
∴ = ( )
角平分线上的任意一点到角的两边的距离相等。
BD CD
热身
练习
判断以下所填结论正确与否
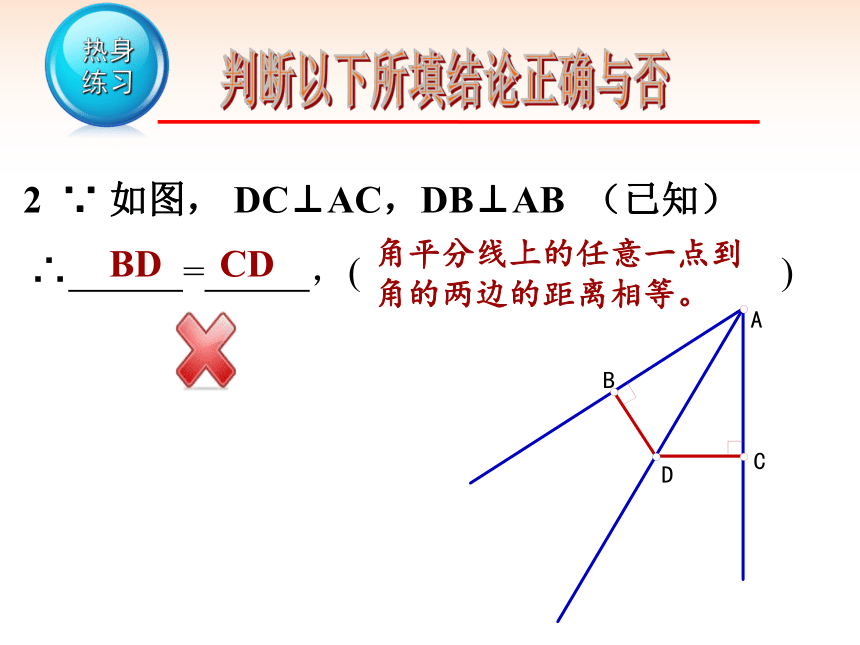
2 ∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的任意一点到角的两边的距离相等。
BD CD
热身
练习
判断以下所填结论正确与否
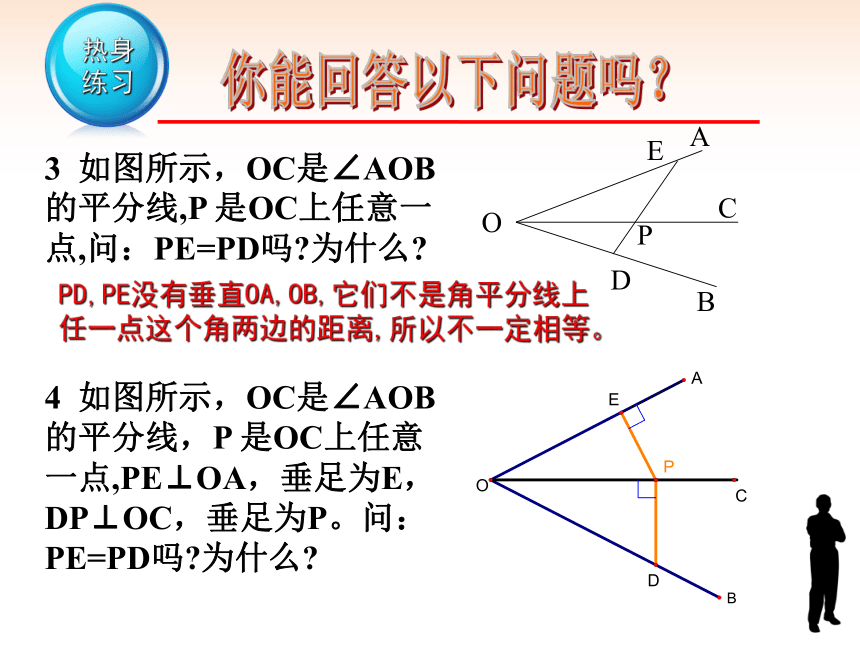
3 如图所示,OC是∠AOB 的平分线,P 是OC上任意一点,问:PE=PD吗?为什么?
O
A
B
E
D
C
P
PD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等。
热身
练习
你能回答以下问题吗?
4 如图所示,OC是∠AOB 的平分线,P 是OC上任意一点,PE⊥OA,垂足为E,DP⊥OC,垂足为P。问:PE=PD吗?为什么?
5 ∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = , ( )
DB
DC
角平分线上的任意一点到角的两边的距离相等。
热身
练习
判断以下所填结论正确与否
通过前面的练习,觉得自己有什么收获吗?
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去
B
A
D
O
P
E
C
性质应用所具备的条件:
角的平分线;
点在该平分线上;
该点到角两边的垂直距离。
性质的结论:
两垂直距离相等。
性质的书写格式:
OP 是 ∠AOB的平分线
\
PD = PE
(角平分线上的任意一点到这个角的两边的距离相等。)
∵
老师提醒:性质的三个条件必须齐全,缺一不可。
角平分线上的点到角的两边的距离相等。
提升认识
1、如图,在Rt△ABC 中,∠C=90°,BD是∠AB C的平分线 ,
A
B
C
DE⊥AB,垂足为E,
E
图中相等的线段有哪些?为什么?
D
∵ ∠C=90° (已知)
∴ DC⊥BC(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA(已知)
∴ DE=DC(角平分线上的任意点到角的两边的距离相等)
答: (1) DE=DC
做完本题后,你对角平分线,又增加了什么认识?
角平分线的性质,为我们证明两线段相等 又提供了新的方法与途径
例题
(2)BE=BC
3
1
2
4
1 如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且DB=10,则点D到AB的距离为_________。
2.如图,△ABC中,∠A=90°,BD平分∠ABC,AD=6,BC=16,DE⊥BC,求△BDC面积
做一做
5
解:∵ ∠A=90° (已知)
∴ DA⊥AB(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA DE⊥BC(已知)
∴ DE=AD=6(角平分线上的任意点到角的两边的距离相等)
E
如图,△ABC的角平分线BM,CN相交于点P,试问点P到三边AB,BC,CA的距离相等吗?为什么?
A
C
N
P
B
M
F
E
D
∵ BM是∠ABC的平分线 P在BM上
又 PE⊥BC PD⊥AB
∴ PE=PD
同理 PE=PF
∴ PE=PD=PF
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去
你能用一句话概括这个结论吗?这一结论和我们前面学习的哪个结论类似?
拓展
如图,P为△ABC中∠A的外角平分线上任一点,且PE⊥BA,PD ⊥AC,E,D分别是垂足,试探索BE+PD与PB的大小关系.
∵ AP是△ABC中∠A的外角平分线,
PE⊥BA,PD ⊥AC,(已知)
∴ PD=PE.(角平分线上的任意一点到角的两边的距离相等)
又 ∵ BE+PE>PB(三角形任意两边之和大于第三边)
∴ BE+PD>PB(等量代换)
A
C
P
B
D
E
解:
动脑筋
我来发言
对自己说:我这节课的收获是……
对同学说:我觉得这节课中的知识要注意
的地方是……
对老师说:我还有这些地方感到困惑……
课堂小结
谢谢 再见
教材130页 练习1,2
及习题A组 1,2
课后
作业
公路BC
B
C
公路AC
公路AB
A
批发
市场
位置?
学以
致用
如图,三条公路AB,BC,AC围成了一个三角形区域,今要在这三角形区域内建一果品批发市场,出于运输方面的考虑,要使果品市场到这三条公路的距离相等,试找出批发市场的位置。
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
课堂小结
1、这节课主要研究了什么问题?得出了哪些结论?
2、你有何体会?
A
B
C
P
三角形ABC的角平分线AP,BP相交于P点,试问P点到三条公路边的距离相等吗?为什么?
A
B
C
公路BC
公路AC
公路AB
批发
市场
F
E
N
老师期望:
养成用数学解释生活的习惯.
学以
致用
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
1△ABC有多少外角平分线?
练 习
2.角的平分线具有怎样的性质?
六 条
角平分线上的点到角两边距离相等
A
B
C
D
F
E
拓展
2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
老师期望:
养成用数学解释生活的习惯.
C●
D●
A
B
O
角平分线的概念
一条射线 将 一个角 分成为两个相等的角,这条射线就叫做这个角的角平分线。
回顾与思考
角平分线的性质
复习回顾:
1)什么是点到直线的距离?
②直线外一点到直线上的所有点的连线中,
垂线段的长度,叫做点到直线的距离
动动手:
那么现在请同学们画出一个角的角平分线。
A
O
B
量一量:
A
O
B
C
1)在角平分线OC上取几点P1、P2 ,
2)作P1D⊥OA;
P1E ⊥OB ;
P2F ⊥ OA;
P2G ⊥ OB;
3)量一量,
你能发现什么?
P1D与P1E;P2F与P2G关系
●
●
E
G
F
D
?
?
?
?
A
B
O
P
D
E
3
4
C
1
2
如图,(1)沿角平分线OC折叠,使∠AOB的边OB与OA重合
(2)∵ PD⊥OA , ,PE⊥OB , ∴∠PDO=∠PEO=90° 又∵∠1=∠2所以∠3=∠4,
从而在沿OC的折叠下,射线PE与射线PD重合,
于是点E与点D重合,所以PD=PE
已知:点P是∠AOB角平分线上的任意一点, PD⊥OA,垂足为D,PE⊥OB,垂足为E
求证:PD=PE
性质定理的证明
角平分线上的任意一点到角的两边的距离相等。
1 ∵ 如图,AD平分∠BAC(已知)
∴ = ( )
角平分线上的任意一点到角的两边的距离相等。
BD CD
热身
练习
判断以下所填结论正确与否
2 ∵ 如图, DC⊥AC,DB⊥AB (已知)
∴ = ,( )
角平分线上的任意一点到角的两边的距离相等。
BD CD
热身
练习
判断以下所填结论正确与否
3 如图所示,OC是∠AOB 的平分线,P 是OC上任意一点,问:PE=PD吗?为什么?
O
A
B
E
D
C
P
PD,PE没有垂直OA,OB,它们不是角平分线上任一点这个角两边的距离,所以不一定相等。
热身
练习
你能回答以下问题吗?
4 如图所示,OC是∠AOB 的平分线,P 是OC上任意一点,PE⊥OA,垂足为E,DP⊥OC,垂足为P。问:PE=PD吗?为什么?
5 ∵ AD平分∠BAC, DC⊥AC,DB⊥AB (已知)
∴ = , ( )
DB
DC
角平分线上的任意一点到角的两边的距离相等。
热身
练习
判断以下所填结论正确与否
通过前面的练习,觉得自己有什么收获吗?
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去
B
A
D
O
P
E
C
性质应用所具备的条件:
角的平分线;
点在该平分线上;
该点到角两边的垂直距离。
性质的结论:
两垂直距离相等。
性质的书写格式:
OP 是 ∠AOB的平分线
\
PD = PE
(角平分线上的任意一点到这个角的两边的距离相等。)
∵
老师提醒:性质的三个条件必须齐全,缺一不可。
角平分线上的点到角的两边的距离相等。
提升认识
1、如图,在Rt△ABC 中,∠C=90°,BD是∠AB C的平分线 ,
A
B
C
DE⊥AB,垂足为E,
E
图中相等的线段有哪些?为什么?
D
∵ ∠C=90° (已知)
∴ DC⊥BC(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA(已知)
∴ DE=DC(角平分线上的任意点到角的两边的距离相等)
答: (1) DE=DC
做完本题后,你对角平分线,又增加了什么认识?
角平分线的性质,为我们证明两线段相等 又提供了新的方法与途径
例题
(2)BE=BC
3
1
2
4
1 如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线交BC于D,BC=15,且DB=10,则点D到AB的距离为_________。
2.如图,△ABC中,∠A=90°,BD平分∠ABC,AD=6,BC=16,DE⊥BC,求△BDC面积
做一做
5
解:∵ ∠A=90° (已知)
∴ DA⊥AB(垂直的定义)
又∵ BD是∠ABC的平分线
∵ DE⊥BA DE⊥BC(已知)
∴ DE=AD=6(角平分线上的任意点到角的两边的距离相等)
E
如图,△ABC的角平分线BM,CN相交于点P,试问点P到三边AB,BC,CA的距离相等吗?为什么?
A
C
N
P
B
M
F
E
D
∵ BM是∠ABC的平分线 P在BM上
又 PE⊥BC PD⊥AB
∴ PE=PD
同理 PE=PF
∴ PE=PD=PF
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去
你能用一句话概括这个结论吗?这一结论和我们前面学习的哪个结论类似?
拓展
如图,P为△ABC中∠A的外角平分线上任一点,且PE⊥BA,PD ⊥AC,E,D分别是垂足,试探索BE+PD与PB的大小关系.
∵ AP是△ABC中∠A的外角平分线,
PE⊥BA,PD ⊥AC,(已知)
∴ PD=PE.(角平分线上的任意一点到角的两边的距离相等)
又 ∵ BE+PE>PB(三角形任意两边之和大于第三边)
∴ BE+PD>PB(等量代换)
A
C
P
B
D
E
解:
动脑筋
我来发言
对自己说:我这节课的收获是……
对同学说:我觉得这节课中的知识要注意
的地方是……
对老师说:我还有这些地方感到困惑……
课堂小结
谢谢 再见
教材130页 练习1,2
及习题A组 1,2
课后
作业
公路BC
B
C
公路AC
公路AB
A
批发
市场
位置?
学以
致用
如图,三条公路AB,BC,AC围成了一个三角形区域,今要在这三角形区域内建一果品批发市场,出于运输方面的考虑,要使果品市场到这三条公路的距离相等,试找出批发市场的位置。
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
课堂小结
1、这节课主要研究了什么问题?得出了哪些结论?
2、你有何体会?
A
B
C
P
三角形ABC的角平分线AP,BP相交于P点,试问P点到三条公路边的距离相等吗?为什么?
A
B
C
公路BC
公路AC
公路AB
批发
市场
F
E
N
老师期望:
养成用数学解释生活的习惯.
学以
致用
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.
A
B
C
D
E
P
F
G
H
B
P
1△ABC有多少外角平分线?
练 习
2.角的平分线具有怎样的性质?
六 条
角平分线上的点到角两边距离相等
A
B
C
D
F
E
拓展
2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
老师期望:
养成用数学解释生活的习惯.
C●
D●
A
B
O
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
