2020--2021学年八年级数学北师大版下册第二章2.6 一元一次不等式组(第2课时)课件(30张)
文档属性
| 名称 | 2020--2021学年八年级数学北师大版下册第二章2.6 一元一次不等式组(第2课时)课件(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 548.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 13:18:05 | ||
图片预览








文档简介
2.6 一元一次不等式组
(第2课时)
北师大版 八年级 数学 下册
为了美化环境,培养中学生的爱国主义情操,团省委组织部分中学的团员去西山植树,某校团委领到一批树苗,若每人植4棵,还剩37棵,若每人植6棵,最后一人有树植,但不足3棵,这批树苗共有________棵.?
121
导入新知
你是怎么计算的?
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意.
素养目标
思考:在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
所以,x的取值范围为4利用三角形三边关系可知:
知识点 1
较复杂的一元一次不等式组的解法
探究新知
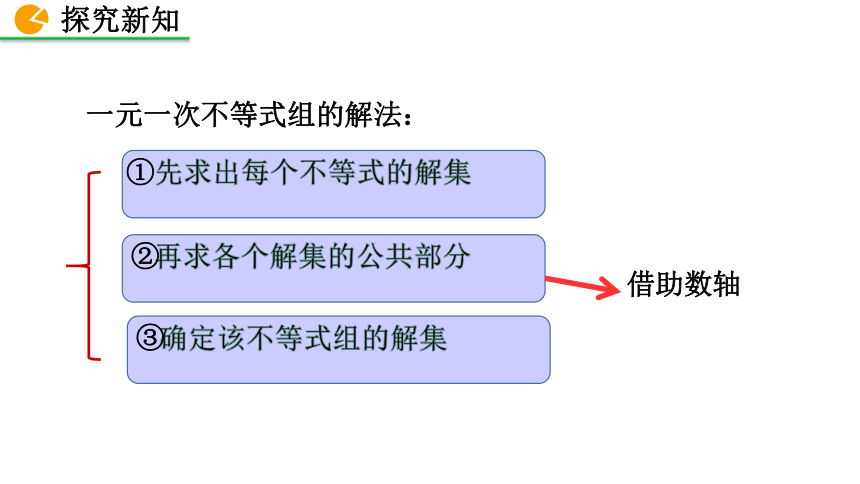
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
探究新知
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式①②的解集
所以,该不等式组的解集是
探究新知
①
②
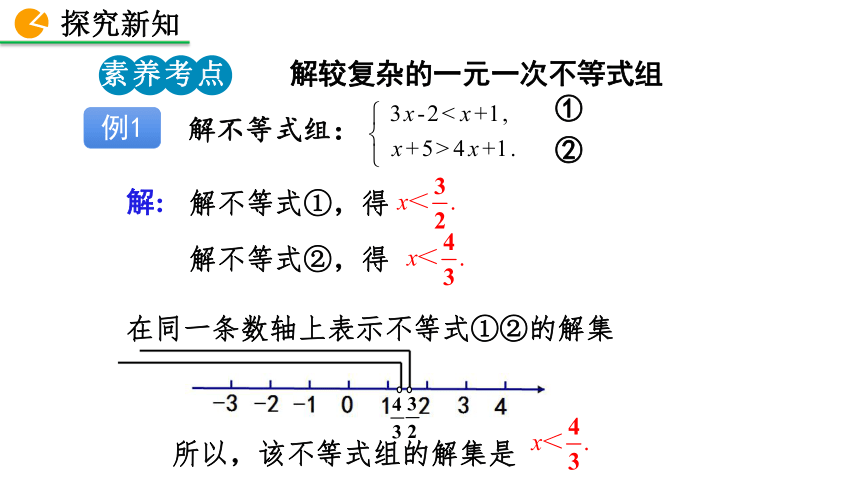
解不等式组:
例1
素养考点 1
解较复杂的一元一次不等式组
解:
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式①②的解集
所以,该不等式组的解集是
探究新知
解不等式组:
①
②
例2
解:
●
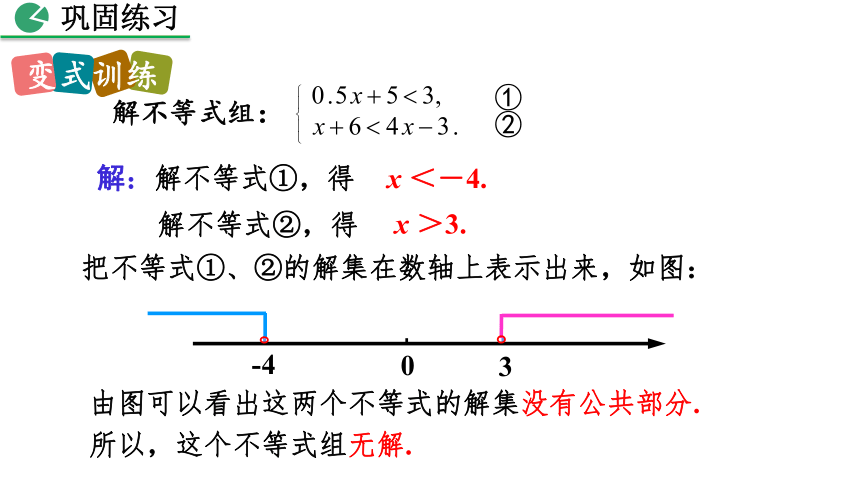
解:解不等式①,得
x <-4.
解不等式②,得
x >3.
解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-4
3
巩固练习
变式训练
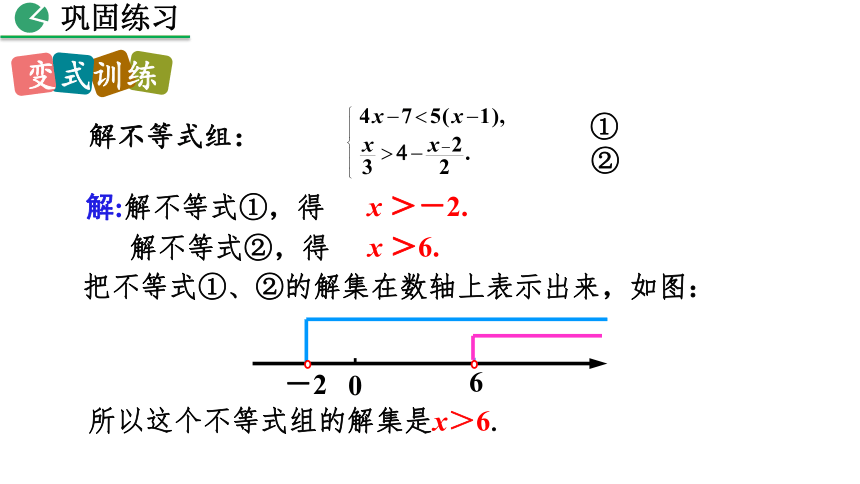
解不等式组:
①
②
解:解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
所以这个不等式组的解集是x>6.
巩固练习
变式训练
B
探究新知
不等式组 有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6C.-6例3
探究新知
方法总结
已知不等式组的解集求未知系数的方法
(1)求出不等式组中各个不等式的解(用未知系数表示).
(2)根据原不等式组解集的情况列出关于未知系数的不等式(组)(尤其考虑是否带有等号).
(3)解不等式求出未知系数的范围.
若关于x的不等式组 的所有整数解的和是-7,则m的取值范围是_____________________.?
-3变式训练
巩固练习
思考:已知三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,你能确定a的取值范围吗?
由题意,得
解不等式①得 ,
解不等式②得 ,
所以,该不等式组的解集是
小
大
解:
探究新知
知识点 2
一元一次不等式组的应用
已知点 在第二象限,则m 的取值范围是什么?
由题意,得
解不等式①,得
解不等式②,得
所以,该不等式组的解集是m>1
解:
探究新知
思考:
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例1 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
探究新知
素养考点 2
一元一次不等式组的应用
村庄
清理养鱼
网箱人数/人
清理捕鱼
网箱人数/人
总支出/元
A
15
9
57 000
B
10
16
68 000
探究新知
“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如表所示:
例2
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元?
解:设清理养鱼网箱和捕鱼网箱的人均支出费用分别为x元、y元
根据题意,得
解得
答:清理养鱼网箱和捕鱼网箱的人均支出费用分别为2 000元,3 000元
探究新知
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调40人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过102 000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
解:设分配a人清理养鱼网箱,则分配(40-a)人清理捕鱼网箱根据题意,得
探究新知
解得18≤a<20.
∵a为正整数,∴a=18或19.
∴一共有2种分配方案,分别为:
方案一:分配18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:分配19人清理养鱼网箱,21人清理捕鱼网箱.
总结:
①列一元一次不等式组解实际问题的一般步骤:
审题——设元——列不等式(组)——求解——检验——作答.
②数学建模的思想方法.
③注意:要根据实际问题的意义确定数学模型的解.
探究新知
巩固练习
变式训练
阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧购买10盒蛋糕,花费的金额不超过2 500元.若她将蛋糕分给75位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?
解:设阿慧购买桂圆蛋糕x盒,则购买金爽蛋糕(10-x)盒.
由题意,得
∵x为整数,∴x=3,
答:阿慧花2450元购买蛋糕.
解得 ,
A
连接中考
(2020?襄阳)不等式组 中两个不等式的解集在数轴上表示正确的是( )
1.解下列不等式组:
解:
(1)
课堂检测
解不等式① ,得
解不等式②,得
所以,该不等式组的解集是
①
②
(2)
解不等式① ,得
解不等式②,得
所以,该不等式组的解集是
基础巩固题
①
②
(1)
(2)
2.已知不等式组 有解,则a的取值范围为( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
课堂检测
基础巩固题
3.在方程组 中,若-3≤x-y<0,则k的取值范围是___________.
?4.把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,则共有学生人数为 ( )
A.6人 B.5人
C.6人或5人 D.4人
A
课堂检测
基础巩固题
已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
所以 (a+1)(b-1)=2×(-3)=-6.
解得
b= -2
a= 1
课堂检测
能力提升题
我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36 kg,乙种制作材料29 kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料
需乙种材料
1件A型陶艺品
0.9 kg
0.3 kg
1件B型陶艺品
0.4 kg
1 kg
课堂检测
拓广探索题
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
课堂检测
解:(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500 .
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元?
课堂检测
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第2课时)
北师大版 八年级 数学 下册
为了美化环境,培养中学生的爱国主义情操,团省委组织部分中学的团员去西山植树,某校团委领到一批树苗,若每人植4棵,还剩37棵,若每人植6棵,最后一人有树植,但不足3棵,这批树苗共有________棵.?
121
导入新知
你是怎么计算的?
1.解较复杂的一元一次不等式组.
2.能根据具体问题中的数量关系,得出一元一次不等式组,解决简单的实际问题,并能根据实际问题的实际意义,检验结果是否符合题意.
素养目标
思考:在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形?
所以,x的取值范围为4
知识点 1
较复杂的一元一次不等式组的解法
探究新知
先求出每个不等式的解集
①
再求各个解集的公共部分
②
确定该不等式组的解集
③
借助数轴
一元一次不等式组的解法:
探究新知
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式①②的解集
所以,该不等式组的解集是
探究新知
①
②
解不等式组:
例1
素养考点 1
解较复杂的一元一次不等式组
解:
解不等式①,得
解不等式②,得
在同一条数轴上表示不等式①②的解集
所以,该不等式组的解集是
探究新知
解不等式组:
①
②
例2
解:
●
解:解不等式①,得
x <-4.
解不等式②,得
x >3.
解不等式组:
①
②
把不等式①、②的解集在数轴上表示出来,如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-4
3
巩固练习
变式训练
解不等式组:
①
②
解:解不等式①,得
x >-2.
解不等式②,得
x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
所以这个不等式组的解集是x>6.
巩固练习
变式训练
B
探究新知
不等式组 有3个整数解,则a的取值范围是( )
A.-6≤a<-5 B.-6
探究新知
方法总结
已知不等式组的解集求未知系数的方法
(1)求出不等式组中各个不等式的解(用未知系数表示).
(2)根据原不等式组解集的情况列出关于未知系数的不等式(组)(尤其考虑是否带有等号).
(3)解不等式求出未知系数的范围.
若关于x的不等式组 的所有整数解的和是-7,则m的取值范围是_____________________.?
-3
巩固练习
思考:已知三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,你能确定a的取值范围吗?
由题意,得
解不等式①得 ,
解不等式②得 ,
所以,该不等式组的解集是
小
大
解:
探究新知
知识点 2
一元一次不等式组的应用
已知点 在第二象限,则m 的取值范围是什么?
由题意,得
解不等式①,得
解不等式②,得
所以,该不等式组的解集是m>1
解:
探究新知
思考:
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例1 用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算:有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
探究新知
素养考点 2
一元一次不等式组的应用
村庄
清理养鱼
网箱人数/人
清理捕鱼
网箱人数/人
总支出/元
A
15
9
57 000
B
10
16
68 000
探究新知
“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如表所示:
例2
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元?
解:设清理养鱼网箱和捕鱼网箱的人均支出费用分别为x元、y元
根据题意,得
解得
答:清理养鱼网箱和捕鱼网箱的人均支出费用分别为2 000元,3 000元
探究新知
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调40人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过102 000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
解:设分配a人清理养鱼网箱,则分配(40-a)人清理捕鱼网箱根据题意,得
探究新知
解得18≤a<20.
∵a为正整数,∴a=18或19.
∴一共有2种分配方案,分别为:
方案一:分配18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:分配19人清理养鱼网箱,21人清理捕鱼网箱.
总结:
①列一元一次不等式组解实际问题的一般步骤:
审题——设元——列不等式(组)——求解——检验——作答.
②数学建模的思想方法.
③注意:要根据实际问题的意义确定数学模型的解.
探究新知
巩固练习
变式训练
阿慧在店内购买两种蛋糕当伴手礼,如图为蛋糕的价目表.已知阿慧购买10盒蛋糕,花费的金额不超过2 500元.若她将蛋糕分给75位同事,每人至少能拿到一个蛋糕,则阿慧花多少元购买蛋糕?
解:设阿慧购买桂圆蛋糕x盒,则购买金爽蛋糕(10-x)盒.
由题意,得
∵x为整数,∴x=3,
答:阿慧花2450元购买蛋糕.
解得 ,
A
连接中考
(2020?襄阳)不等式组 中两个不等式的解集在数轴上表示正确的是( )
1.解下列不等式组:
解:
(1)
课堂检测
解不等式① ,得
解不等式②,得
所以,该不等式组的解集是
①
②
(2)
解不等式① ,得
解不等式②,得
所以,该不等式组的解集是
基础巩固题
①
②
(1)
(2)
2.已知不等式组 有解,则a的取值范围为( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
课堂检测
基础巩固题
3.在方程组 中,若-3≤x-y<0,则k的取值范围是___________.
?
A.6人 B.5人
C.6人或5人 D.4人
A
课堂检测
基础巩固题
已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少?
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
所以 (a+1)(b-1)=2×(-3)=-6.
解得
b= -2
a= 1
课堂检测
能力提升题
我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36 kg,乙种制作材料29 kg,制作A,B两种型号的陶艺品用料情况如表所示:
需甲种材料
需乙种材料
1件A型陶艺品
0.9 kg
0.3 kg
1件B型陶艺品
0.4 kg
1 kg
课堂检测
拓广探索题
(1)设制作B型陶艺品x件,求x的取值范围.
(2)请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数.
解:(1)由题意知:
解不等式组得:18≤x≤20.
(2)A型32件,B型18件;A型31件,B型19件;A型30件,B型20件.
课堂检测
解:(3)设获得的总利润为y元,
由题意知:y=10(50-x)+15x=5x+500 .
∵5>0,∴y随x的增大而增大.
则当x=20时,y最大值=600元.
故制作A型陶艺品30件,B型陶艺品20件时,
获得的利润最大为600元.
(3)若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元?
课堂检测
一元一次不等式组
利用公共部分确定不等式组的解集
分步解不等式
去括号、去分母
解较复杂的一元一次不等式组
→
实际应用(整数解)
→
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
