5.2平行线及其判定 同步课时训练(含解析)
文档属性
| 名称 | 5.2平行线及其判定 同步课时训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 07:48:47 | ||
图片预览




文档简介
七年级下册5.2平行线及其判定课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
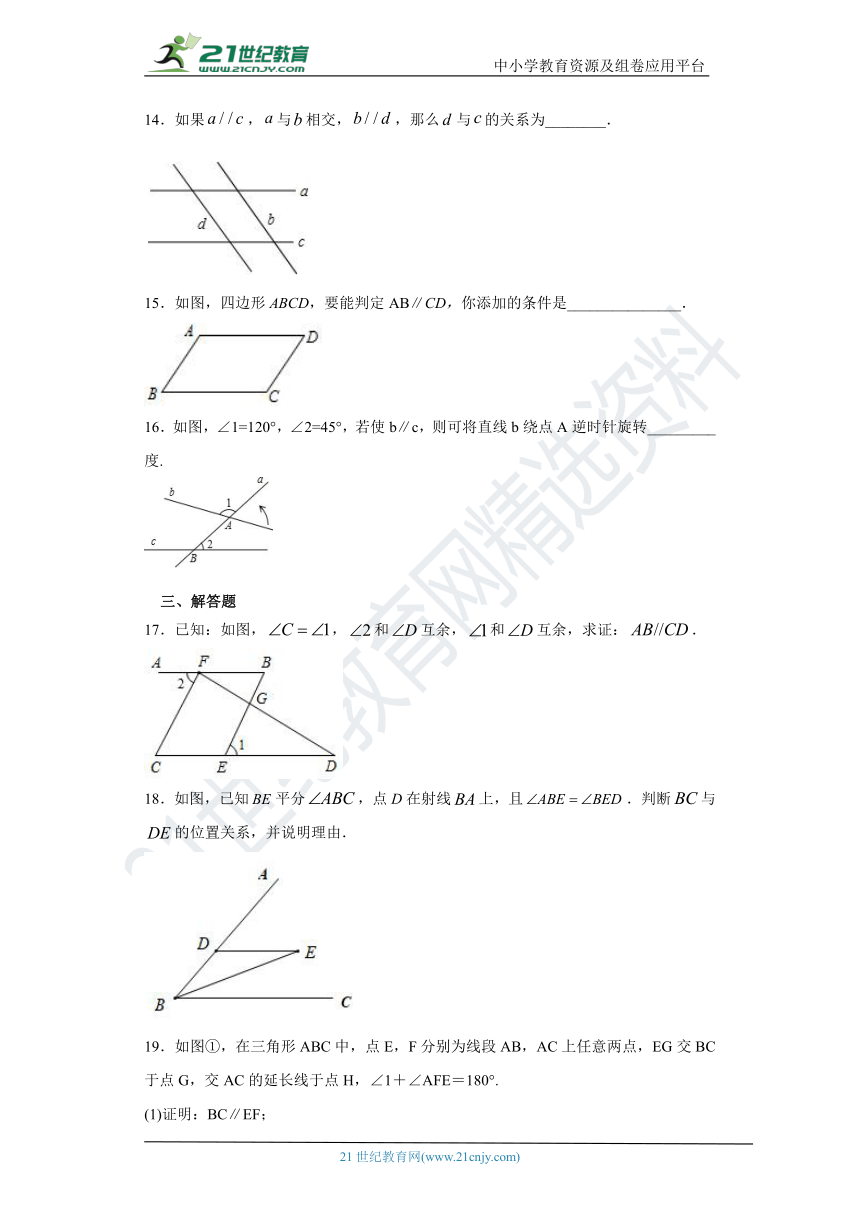
1.如图,能判断false的条件是( )
A.false B.false
C.false D.false
2.如图,下列条件能判断false的是( )
A.false B.false C.false D.false
3.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠3=∠5 B.∠4=∠7
C.∠2+∠3=180° D.∠1=∠3
4.如图,在下列给出的条件中,能判定false的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
5.如图,点E在false的延长线上,则下列条件中,不能判定false的是( )
A.false B.false C.false D.false
6.下列语句正确的个数是( )
①直线外一点与直线上各点连接的所有线段中,垂线段最短
②两点之间直线最短
③在同一平面内,两条不重合的直线位置关系不平行必相交
④两点确定一条直线
A.1 B.2 C.3 D.4
7.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
8.在同一平面内,两条直线的位置关系可能是( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
9.如图,直线a,b被直线c所截,现给出下列四个条件:(1)false;(2)false;(3)false;(4)false,其中能判定false的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
10.庆庆在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向左拐30°第二次向右拐30° B.第一次向右拐50°第二次向左拐130°
C.第一次向右拐50°第二次向右拐130° D.第一次向左拐50°第二次向左拐130°
二、填空题
11.如图,点false在false延长线上,四个条件中:①false;②false,③false;④false;⑤false,能判断false的是______.(填序号).
12.如图,点E在false的延长线上,下列四个条件:①false;②false;③false;④false.其中能判断false的是__________________(填写正确的序号即可).
13.给出下列说法:①同角的补角相等;②相等的角是对顶角;③两点确定一条直线;④过一点有且只有一条直线与已知直线平行,其中正确的有___个.
14.如果false,false与false相交,false,那么false与false的关系为________.
?
15.如图,四边形ABCD,要能判定AB∥CD,你添加的条件是_______________.
16.如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转_________度.
三、解答题
17.已知:如图,false,false和false互余,false和false互余,求证:false.
18.如图,已知false平分false,点D在射线false上,且false.判断false与false的位置关系,并说明理由.
19.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
20.如图,在false中,false是false边上的一点,false,false,将false沿false折叠得到false,false与false交于点false.
(1)求false和false的度数;
(2)若false,问:false//false吗,请说明理由.
参考答案
1.A
解:A、∵∠DAC=∠BCA,∴AD∥BC(内错角相等,两直线平行),故A能判断;
B、根据“∠DCB+∠ABC=180°”只能判定“DC∥AB”,而非AD∥BC,故B不能判断;
C、根据“∠ABD=∠BDC”只能判定“DC∥AB”,而非AD∥BC,故C不能判断;
D、根据“∠BAC=∠ACD”只能判定“DC∥AB”,而非AD∥BC,故D不能判断;
故选:A.
2.C
解:A、∠D+∠DAB=180°,则AB∥DC,故选项错误;
B、∠1=∠2,则AB∥DC,故选项错误;
C、∠3=∠4,AD∥BC,故选项正确;
D、∠4=∠5,不能判定,故选项错误;
故选:C.
3.A
解:A选项,
∵∠3=∠5(已知),
∴a∥b(内错角相等,两直线平行).
B选项,∠4=∠7,∠4与∠7无关系,不能判定平行;
C选项,∠2+∠3=180°,∠2与∠3为邻补角,不能判定平行;
D选项,∠1=∠3,∠1与∠3为对顶角,不能判定两直线平行;
故选:A.
4.C
解:A、∵∠4=∠3,∴DE∥AC,不符合题意;
B、∵∠1=∠A,∴DE∥AC,不符合题意;
C、∵∠1=∠3,∴DF∥AB,符合题意;
D、∵∠4+∠2=180°,∴DE∥AC,不符合题意;
故选:C.
5.B
解:A、如果false,那么false,故该项不符合题意;
B、如果false,那么AD∥BC,故该项符合题意;
C、如果false,那么false,故该项不符合题意;
D、如果false,那么false,故该项不符合题意;
故选:B.
6.C
解:①直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;
②两点之间直线最短,直线可以两边无限延伸不可测,该说法错误;
③在同一平面内,两条不重合的直线位置关系不平行必相交,正确;
④两点确定一条直线,正确.
正确的有:①③④,
故选:C.
7.D
解:∵∠1=∠2=60°,
∴a∥b,
∵∠2=∠3,
∴b∥c,
∴a∥c,
故选:D.
8.A
解:在同一平面内,两条直线只有两种位置关系:相交或平行,
故选:A.
9.A
解:false
false 故(1)可判定;
false
false
false 故(2)可判定;
false,不能判定false故(3)不能判定;
false,不能判定false故(4)不能判定.
故选:false
10.A
解:A、如图:两次拐弯后,行驶的方向与原来的方向相同,故本选项符合题意;
B、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项不符合题意;
C、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项不符合题意;
D、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项吧符合题意;
故选:A.
11.②③
解:①∵∠1=∠3,∴AD∥BC;
②∵∠2+∠5=180°,∵∠5=∠AGC,∴∠2+∠AGC=180°,∴AB∥DC;
③∵∠4=∠B,∴AB∥DC;
④∠B=∠D无法判断出AD∥BC;
⑤∵∠D+∠BCD=180°,∴AD∥BC.
故答案为:②③.
12.②③④
解:①∵false,∴AB∥CD;故①错误;
②∵false,∴false;故②正确;
③∵false,∴false;故③正确;
④∵false,∴false;故④正确;
故答案为:②③④;
13.2
解:同角的补角相等,故①符合题意;
对顶角相等,但相等的角不一定是对顶角,故②不符合题意;
两点确定一条直线,故③符合题意;
过直线外一点有且只有一条直线与已知直线平行,故④不符合题意;
故答案为:2.
14.相交
解:false和false的关系是:相交.
故答案为:相交.
15.false(或false)
解:条件为:∠A+∠D=180?或∠B+∠C=180 ?,
∵∠A+∠D=180?(已知),
∴AB∥CD(同旁内角互补,两直线平行).
或
∵∠B+∠C=180 ?(已知),
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:∠A+∠D=180?或∠B+∠C=180 ?,
16.15
解:如图:
∵∠1=120°,
∴∠3=60°,
∵∠2=45°,
∴当∠3=∠2=45°时,b∥c,
∴直线b绕点A逆时针旋转60°-45°=15°.
故答案为:15.
17.证明见详解
解:证明:∵∠1和∠D互余,∠2和∠D互余,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
18.BC∥DE;理由见解析
解:BC∥DE;理由如下:
因为false平分false,
所以∠ABE=∠CBE,
因为false,
所以∠CBE=∠BED,
所以BC∥DE.
19.(1)见解析;(2) 见解析.
解:证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
20.(1) 105°,30°;(2)平行,理由见解析
解:(1)由折叠前后对应的角相等可知,∠BAD=∠DAF=30°,
∴∠BAF=∠BAD+∠DAF=30°+30°=60°,
在△ABF中,由三角形内角和定理可知,∠AFB=180°-∠BAF-∠B=180°-60°-45°=75°,
∴∠AFC=180°-∠AFB=180°-75°=105°,
在△ABD中,由三角形内角和定理可知,∠ADB=180°-∠BAD-∠B=180°-30°-45°=105°,
∴∠ADF=180°-∠ADB=75°,
由折叠前后对应的角相等可知,∠ADE=∠ADB=105°,
∴∠EDF=∠ADE-∠ADF=105°-75°=30°,
故答案为:105°,30°;
(2) false//false,理由如下:
∵△ABD沿AD折叠得到△AED,∴∠B=∠E=45°,
∵∠E:∠C=3:2,∴∠C=30°,
∴∠C=∠EDF=30°,
∴DE∥AC.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,能判断false的条件是( )
A.false B.false
C.false D.false
2.如图,下列条件能判断false的是( )
A.false B.false C.false D.false
3.如图,直线a,b被直线c所截,下列条件能判断a∥b的是( )
A.∠3=∠5 B.∠4=∠7
C.∠2+∠3=180° D.∠1=∠3
4.如图,在下列给出的条件中,能判定false的是( )
A.∠4=∠3 B.∠1=∠A C.∠1=∠4 D.∠4+∠2=180°
5.如图,点E在false的延长线上,则下列条件中,不能判定false的是( )
A.false B.false C.false D.false
6.下列语句正确的个数是( )
①直线外一点与直线上各点连接的所有线段中,垂线段最短
②两点之间直线最短
③在同一平面内,两条不重合的直线位置关系不平行必相交
④两点确定一条直线
A.1 B.2 C.3 D.4
7.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
8.在同一平面内,两条直线的位置关系可能是( )
A.相交或平行 B.相交或垂直 C.平行或垂直 D.不能确定
9.如图,直线a,b被直线c所截,现给出下列四个条件:(1)false;(2)false;(3)false;(4)false,其中能判定false的条件的序号是( )
A.(1),(2) B.(1),(3) C.(1),(4) D.(3),(4)
10.庆庆在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来的方向相同,这两次拐弯的角度可能是( )
A.第一次向左拐30°第二次向右拐30° B.第一次向右拐50°第二次向左拐130°
C.第一次向右拐50°第二次向右拐130° D.第一次向左拐50°第二次向左拐130°
二、填空题
11.如图,点false在false延长线上,四个条件中:①false;②false,③false;④false;⑤false,能判断false的是______.(填序号).
12.如图,点E在false的延长线上,下列四个条件:①false;②false;③false;④false.其中能判断false的是__________________(填写正确的序号即可).
13.给出下列说法:①同角的补角相等;②相等的角是对顶角;③两点确定一条直线;④过一点有且只有一条直线与已知直线平行,其中正确的有___个.
14.如果false,false与false相交,false,那么false与false的关系为________.
?
15.如图,四边形ABCD,要能判定AB∥CD,你添加的条件是_______________.
16.如图,∠1=120°,∠2=45°,若使b∥c,则可将直线b绕点A逆时针旋转_________度.
三、解答题
17.已知:如图,false,false和false互余,false和false互余,求证:false.
18.如图,已知false平分false,点D在射线false上,且false.判断false与false的位置关系,并说明理由.
19.如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
20.如图,在false中,false是false边上的一点,false,false,将false沿false折叠得到false,false与false交于点false.
(1)求false和false的度数;
(2)若false,问:false//false吗,请说明理由.
参考答案
1.A
解:A、∵∠DAC=∠BCA,∴AD∥BC(内错角相等,两直线平行),故A能判断;
B、根据“∠DCB+∠ABC=180°”只能判定“DC∥AB”,而非AD∥BC,故B不能判断;
C、根据“∠ABD=∠BDC”只能判定“DC∥AB”,而非AD∥BC,故C不能判断;
D、根据“∠BAC=∠ACD”只能判定“DC∥AB”,而非AD∥BC,故D不能判断;
故选:A.
2.C
解:A、∠D+∠DAB=180°,则AB∥DC,故选项错误;
B、∠1=∠2,则AB∥DC,故选项错误;
C、∠3=∠4,AD∥BC,故选项正确;
D、∠4=∠5,不能判定,故选项错误;
故选:C.
3.A
解:A选项,
∵∠3=∠5(已知),
∴a∥b(内错角相等,两直线平行).
B选项,∠4=∠7,∠4与∠7无关系,不能判定平行;
C选项,∠2+∠3=180°,∠2与∠3为邻补角,不能判定平行;
D选项,∠1=∠3,∠1与∠3为对顶角,不能判定两直线平行;
故选:A.
4.C
解:A、∵∠4=∠3,∴DE∥AC,不符合题意;
B、∵∠1=∠A,∴DE∥AC,不符合题意;
C、∵∠1=∠3,∴DF∥AB,符合题意;
D、∵∠4+∠2=180°,∴DE∥AC,不符合题意;
故选:C.
5.B
解:A、如果false,那么false,故该项不符合题意;
B、如果false,那么AD∥BC,故该项符合题意;
C、如果false,那么false,故该项不符合题意;
D、如果false,那么false,故该项不符合题意;
故选:B.
6.C
解:①直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;
②两点之间直线最短,直线可以两边无限延伸不可测,该说法错误;
③在同一平面内,两条不重合的直线位置关系不平行必相交,正确;
④两点确定一条直线,正确.
正确的有:①③④,
故选:C.
7.D
解:∵∠1=∠2=60°,
∴a∥b,
∵∠2=∠3,
∴b∥c,
∴a∥c,
故选:D.
8.A
解:在同一平面内,两条直线只有两种位置关系:相交或平行,
故选:A.
9.A
解:false
false 故(1)可判定;
false
false
false 故(2)可判定;
false,不能判定false故(3)不能判定;
false,不能判定false故(4)不能判定.
故选:false
10.A
解:A、如图:两次拐弯后,行驶的方向与原来的方向相同,故本选项符合题意;
B、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项不符合题意;
C、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项不符合题意;
D、如图:两次拐弯后,行驶的方向与原来的方向不相同,故本选项吧符合题意;
故选:A.
11.②③
解:①∵∠1=∠3,∴AD∥BC;
②∵∠2+∠5=180°,∵∠5=∠AGC,∴∠2+∠AGC=180°,∴AB∥DC;
③∵∠4=∠B,∴AB∥DC;
④∠B=∠D无法判断出AD∥BC;
⑤∵∠D+∠BCD=180°,∴AD∥BC.
故答案为:②③.
12.②③④
解:①∵false,∴AB∥CD;故①错误;
②∵false,∴false;故②正确;
③∵false,∴false;故③正确;
④∵false,∴false;故④正确;
故答案为:②③④;
13.2
解:同角的补角相等,故①符合题意;
对顶角相等,但相等的角不一定是对顶角,故②不符合题意;
两点确定一条直线,故③符合题意;
过直线外一点有且只有一条直线与已知直线平行,故④不符合题意;
故答案为:2.
14.相交
解:false和false的关系是:相交.
故答案为:相交.
15.false(或false)
解:条件为:∠A+∠D=180?或∠B+∠C=180 ?,
∵∠A+∠D=180?(已知),
∴AB∥CD(同旁内角互补,两直线平行).
或
∵∠B+∠C=180 ?(已知),
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:∠A+∠D=180?或∠B+∠C=180 ?,
16.15
解:如图:
∵∠1=120°,
∴∠3=60°,
∵∠2=45°,
∴当∠3=∠2=45°时,b∥c,
∴直线b绕点A逆时针旋转60°-45°=15°.
故答案为:15.
17.证明见详解
解:证明:∵∠1和∠D互余,∠2和∠D互余,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
18.BC∥DE;理由见解析
解:BC∥DE;理由如下:
因为false平分false,
所以∠ABE=∠CBE,
因为false,
所以∠CBE=∠BED,
所以BC∥DE.
19.(1)见解析;(2) 见解析.
解:证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
20.(1) 105°,30°;(2)平行,理由见解析
解:(1)由折叠前后对应的角相等可知,∠BAD=∠DAF=30°,
∴∠BAF=∠BAD+∠DAF=30°+30°=60°,
在△ABF中,由三角形内角和定理可知,∠AFB=180°-∠BAF-∠B=180°-60°-45°=75°,
∴∠AFC=180°-∠AFB=180°-75°=105°,
在△ABD中,由三角形内角和定理可知,∠ADB=180°-∠BAD-∠B=180°-30°-45°=105°,
∴∠ADF=180°-∠ADB=75°,
由折叠前后对应的角相等可知,∠ADE=∠ADB=105°,
∴∠EDF=∠ADE-∠ADF=105°-75°=30°,
故答案为:105°,30°;
(2) false//false,理由如下:
∵△ABD沿AD折叠得到△AED,∴∠B=∠E=45°,
∵∠E:∠C=3:2,∴∠C=30°,
∴∠C=∠EDF=30°,
∴DE∥AC.
