7.2坐标方法的简单应用 同步课时训练(含解析)
文档属性
| 名称 | 7.2坐标方法的简单应用 同步课时训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 835.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 07:54:50 | ||
图片预览



文档简介
7.2坐标方法的简单应用课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在平面直角坐标系中,把点false向右平移1个单位后所得的点的坐标是( )
A.false B.false C.false D.false
2.在平面直角坐标系中,若点P(-3,-1)向右平移4个单位得到点Q,则点Q在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
3.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
4.如图,false、false的坐标分别为false、false,若将线段false平移到至false,false的坐标为false,则false的坐标为( )
A.false B.false C.false D.false
5.如图,在平面直角坐标系中,线段false的两个端点是false,false.将线段false沿某一方向平移后,若点false的对应点false的坐标为false,则点false的对应点false的坐标为( )
A.false B.false C.false D.false
6.如图,三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,若∠C的度数为x,则∠A1OC的度数为( )
A.x B.90°﹣x C.180°﹣x D.90°+x
7.下列叙述中,不能确定位置的是( )
A.小华在某会场的座位是5排8号 B.某城市位于东经108°,北纬39°
C.A城与B城相距15 km D.船C在观测点A北偏东40°方向上30 km处
8.false三个顶点的坐标分别为false,将false先向左平移1个单位,再向上平移3个单位得到false.则点B的对应点false的坐标为( )
A.false B.false C.false D.false
9.在平面直角坐标系中,将三角形各顶点的纵坐标都加上false,横坐标保持不变,所得图形的位置与原图形相比( )
A.向上平移false个单位 B.向下平移false个单位
C.向右平移false个单位 D.向左平移false个单位
10.在平面直角坐标系中,将点(﹣2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
二、填空题
11.如图,在平面直角坐标系false中,将四边形false先向下平移,再向右平移,得到四边形false,已知点false,点false,点false,则点false的坐标为___.
12.把直线false向上平移后得到直线false,若直线false经过点false,且false则直线false的表达式为_______
13.将点false向右平移4个单位得到点false,则点false的坐标为__________.
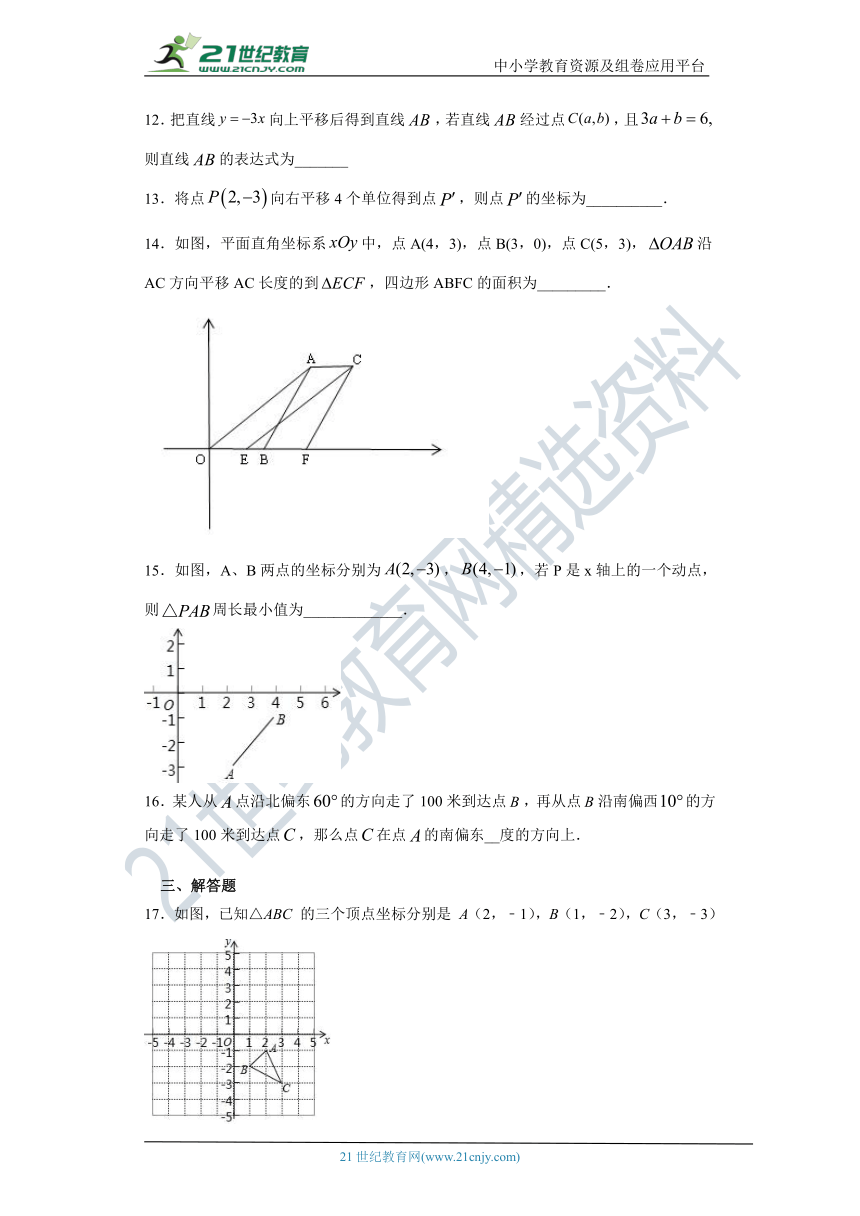
14.如图,平面直角坐标系false中,点A(4,3),点B(3,0),点C(5,3),false沿AC方向平移AC长度的到false,四边形ABFC的面积为_________.
15.如图,A、B两点的坐标分别为false,false,若P是x轴上的一个动点,则false周长最小值为_____________.
16.某人从false点沿北偏东false的方向走了100米到达点false,再从点false沿南偏西false的方向走了100米到达点false,那么点false在点false的南偏东__度的方向上.
三、解答题
17.如图,已知△ABC 的三个顶点坐标分别是 A(2,﹣1),B(1,﹣2),C(3,﹣3)
(1)将△ABC 向上平移 4 个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请写出 B1 坐标,并用恰当的方式表示线段 BB1 上任意一点的坐标;
(3)求△ABC 的面积.
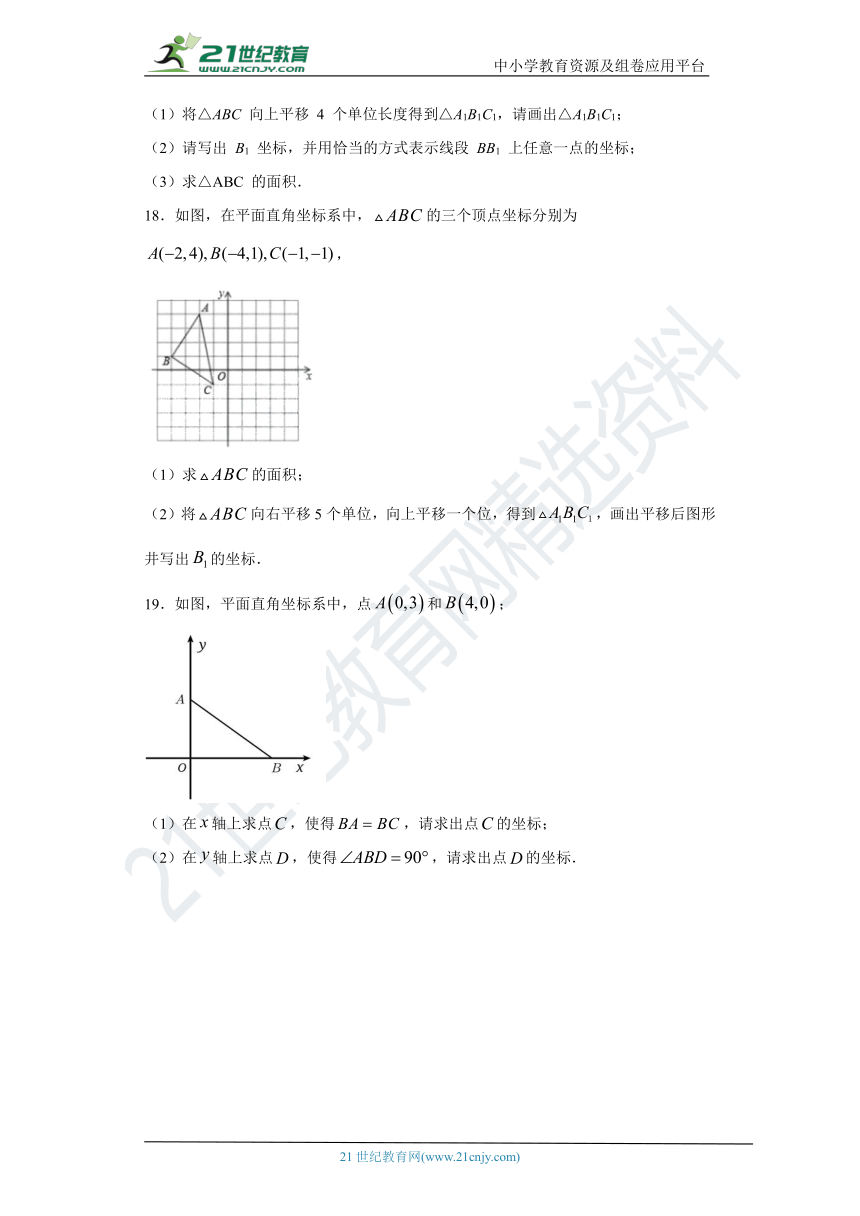
18.如图,在平面直角坐标系中,false的三个顶点坐标分别为false,
(1)求false的面积;
(2)将false向右平移5个单位,向上平移一个位,得到false,画出平移后图形井写出false的坐标.
19.如图,平面直角坐标系中,点false和false;
(1)在false轴上求点false,使得false,请求出点false的坐标;
(2)在false轴上求点false,使得false,请求出点false的坐标.
参考答案
1.D
解:点(2,?1)向右平移 1个单位得到的坐标为(3,-1),
故选D.
2.A
解:∵点P(false3,false1)向右平移4个单位得到点Q,
∴点Q为(1,false1),
∴点Q在第四象限,
故选:A.
3.A
解:∵点false(1,2),
∴先向右平移2个单位长度,再向下平移1个单位长度后的坐标为(1+2,2-1),
即:(3,1).
故选:false.
4.B
解:∵false、false的坐标分别为false、false,
平移后falsefalse,
∴ 线段AB向右平移1个单位,向上平移1个单位,
∴falsefalse向右平移1个单位,向上平移1个单位后
false的坐标的横坐标为:0+1=1,
false的坐标的纵坐标为:2+1=3,
∴ 点falsefalse.
故选:B.
5.C
解:false平移后得到falsefalse
横坐标减小3,纵坐标减小3,
false
即false
故选:C.
6.C
解:∵三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,
∴∠C1=∠C,false,
∴∠COC1=∠C1(两直线平行内错角相等),
∴∠A1OC=180°﹣x,
故选:C.
7.C
解:在平面内,一对有序实数确定一个点的位置,
A.小华在某会场的座位是5排8号,能确定位置,故不符合题意;
B.某城市位于东经108°,北纬39°,能确定位置,故不符合题意;
C. A城与B城相距15 km,没有明确方向,故不能确定其位置,符合题意;
D. 船C在观测点A北偏东40°方向上30 km处,能确定位置,故不符合题意.
故选:C.
8.A
解:∵B(-3,1),向左平移1个单位,再向上平移3个单位得B1(-4,4),
故选:A.
9.A
解:将三角形各顶点的纵坐标都加上3,横坐标保持不变,所得图形的位置与原图形相比向上平移3个单位;
故选:A.
10.C
解:将点P(﹣2,3)向右平移4个单位长度,再向下平移2个单位长度所得到的点坐标为(﹣2+4,3﹣2),即(2,1).
故选:C.
11.(2,1)
解:由A(-3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(-4,3),
∴B1的坐标为(2,1),
故答案为:(2,1).
12.false.
解:设直线y= -3x向上平移了m个单位,
∴直线的解析式为y= -3x+m,
∵直线false经过点false,
∴b=-3a+m,
∵false
∴b=-3a+6,
∴-3a+m=-3a+6,
∴m=6,
∴直线AB的解析式为y=-3x+6,
故答案为:y=-3x+6.
13.false
解:将点P(2,﹣3)向右平移4个单位长度得点P′,
则点P′的坐标为(6,﹣3).
故答案为:(6,﹣3).
14.3
解:∵A(4,3),点C(5,3),
∴AC=5-4=1,false,
∵false沿AC方向平移AC长度的到false,
∴AC=BF,
∴四边形ABFC为平行四边形,
∴四边形ABFC的高为C点到x轴的距离,
∴false,
故答案为:3.
15.false
解:如图,作点B关于x轴的对称点B',连接AB'交x轴于点P,连接PB,
∵点B关于x轴的对称点为点B',点B的坐标为(4,?1),
∴PB=PB',点B'的坐标为(4,1).
∴PA+PB=PA+PB'=AB'.
由两点之间线段最短可知,此时PA+PB的值最小,
∵AB的长不变,
∴△PAB的周长的最小.
∵A(2,?3),B(4,?1),B'(4,1),
∴AB=false,
AB'=false.
∴△PAB的周长的最小值=PA+PB+AB=AB'+AB=false.
故答案为:false.
16.55
解:根据题意作图:
∵从A点沿北偏东60°的方向走了100米到达点B,从点B沿南偏西10°的方向走了100米到达点C,
∴∠1+∠2=60°,AB=BC=100,
∴∠2=50°,且△ABC是等腰三角形,
∴∠BAC=false=65°,
∴∠5=180°-65°-60°=55°,
∴点C在点A的南偏东55°的方向上.
故答案为:55.
17.(1)答案见解析;(2)(1,y)(false);(3)false.
解:(1)如图,false即为所画.
(2)线段false上任意一点的坐标为(1,y)(false).
(3)取点D(1,-3)、E(3,-1)、F(1,-1),分别连接CD、CE、DF、EF.则四边形CDFE为边长为2的正方形,AF=BF=AE=BD=1、CD=CE=2.
∴false.
18.(1)false;(2)图见解析,false
解:(1)false;
(2)平移后如图所示,false.
19.(1)(-1,0)或(9,0);(2)(0,-false).
解:(1)平面直角坐标系中,点false和false,
OA=3,OB=4,∠AOB=90 ?,
在Rt△AOB中,由勾股定理AB=false ,
以B为圆心,AB长为半径在x轴上截取两点C1、C2,
△ABC1是等腰三角形,AB=BC1=5,OC1=BC1-OB=5-4=1,则C1坐标为(-1,0),
△ABC2是等腰三角形,AB=BC2=5,OC2=BC2+OB=5+4=9,则C1坐标为(9,0),
则C点坐标为(-1,0)或(9,0),
(2)设OD=x,
∠BOD=90?,
在Rt△BOD中BD2=OB2+OD2=16+x2,
由false,
AD=3+x,
由勾股定理AD2=AB2+BD2,
false,
解这个方程得false,
则D点的坐标为(0,-false).
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在平面直角坐标系中,把点false向右平移1个单位后所得的点的坐标是( )
A.false B.false C.false D.false
2.在平面直角坐标系中,若点P(-3,-1)向右平移4个单位得到点Q,则点Q在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
3.在平面直角坐标系内,将点A(1,2)先向右平移2个单位长度,再向下平移1个单位长度,则平移后所得点的坐标是( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
4.如图,false、false的坐标分别为false、false,若将线段false平移到至false,false的坐标为false,则false的坐标为( )
A.false B.false C.false D.false
5.如图,在平面直角坐标系中,线段false的两个端点是false,false.将线段false沿某一方向平移后,若点false的对应点false的坐标为false,则点false的对应点false的坐标为( )
A.false B.false C.false D.false
6.如图,三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,若∠C的度数为x,则∠A1OC的度数为( )
A.x B.90°﹣x C.180°﹣x D.90°+x
7.下列叙述中,不能确定位置的是( )
A.小华在某会场的座位是5排8号 B.某城市位于东经108°,北纬39°
C.A城与B城相距15 km D.船C在观测点A北偏东40°方向上30 km处
8.false三个顶点的坐标分别为false,将false先向左平移1个单位,再向上平移3个单位得到false.则点B的对应点false的坐标为( )
A.false B.false C.false D.false
9.在平面直角坐标系中,将三角形各顶点的纵坐标都加上false,横坐标保持不变,所得图形的位置与原图形相比( )
A.向上平移false个单位 B.向下平移false个单位
C.向右平移false个单位 D.向左平移false个单位
10.在平面直角坐标系中,将点(﹣2,3)先向右平移4个单位长度,再向下平移2个单位长度,得到的点的坐标为( )
A.(2,5) B.(﹣6,5) C.(2,1) D.(﹣6,1)
二、填空题
11.如图,在平面直角坐标系false中,将四边形false先向下平移,再向右平移,得到四边形false,已知点false,点false,点false,则点false的坐标为___.
12.把直线false向上平移后得到直线false,若直线false经过点false,且false则直线false的表达式为_______
13.将点false向右平移4个单位得到点false,则点false的坐标为__________.
14.如图,平面直角坐标系false中,点A(4,3),点B(3,0),点C(5,3),false沿AC方向平移AC长度的到false,四边形ABFC的面积为_________.
15.如图,A、B两点的坐标分别为false,false,若P是x轴上的一个动点,则false周长最小值为_____________.
16.某人从false点沿北偏东false的方向走了100米到达点false,再从点false沿南偏西false的方向走了100米到达点false,那么点false在点false的南偏东__度的方向上.
三、解答题
17.如图,已知△ABC 的三个顶点坐标分别是 A(2,﹣1),B(1,﹣2),C(3,﹣3)
(1)将△ABC 向上平移 4 个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请写出 B1 坐标,并用恰当的方式表示线段 BB1 上任意一点的坐标;
(3)求△ABC 的面积.
18.如图,在平面直角坐标系中,false的三个顶点坐标分别为false,
(1)求false的面积;
(2)将false向右平移5个单位,向上平移一个位,得到false,画出平移后图形井写出false的坐标.
19.如图,平面直角坐标系中,点false和false;
(1)在false轴上求点false,使得false,请求出点false的坐标;
(2)在false轴上求点false,使得false,请求出点false的坐标.
参考答案
1.D
解:点(2,?1)向右平移 1个单位得到的坐标为(3,-1),
故选D.
2.A
解:∵点P(false3,false1)向右平移4个单位得到点Q,
∴点Q为(1,false1),
∴点Q在第四象限,
故选:A.
3.A
解:∵点false(1,2),
∴先向右平移2个单位长度,再向下平移1个单位长度后的坐标为(1+2,2-1),
即:(3,1).
故选:false.
4.B
解:∵false、false的坐标分别为false、false,
平移后falsefalse,
∴ 线段AB向右平移1个单位,向上平移1个单位,
∴falsefalse向右平移1个单位,向上平移1个单位后
false的坐标的横坐标为:0+1=1,
false的坐标的纵坐标为:2+1=3,
∴ 点falsefalse.
故选:B.
5.C
解:false平移后得到falsefalse
横坐标减小3,纵坐标减小3,
false
即false
故选:C.
6.C
解:∵三角形ABC沿AB方向向右平移后到达三角形A1B1C1的位置,BC与A1C1相交于点O,
∴∠C1=∠C,false,
∴∠COC1=∠C1(两直线平行内错角相等),
∴∠A1OC=180°﹣x,
故选:C.
7.C
解:在平面内,一对有序实数确定一个点的位置,
A.小华在某会场的座位是5排8号,能确定位置,故不符合题意;
B.某城市位于东经108°,北纬39°,能确定位置,故不符合题意;
C. A城与B城相距15 km,没有明确方向,故不能确定其位置,符合题意;
D. 船C在观测点A北偏东40°方向上30 km处,能确定位置,故不符合题意.
故选:C.
8.A
解:∵B(-3,1),向左平移1个单位,再向上平移3个单位得B1(-4,4),
故选:A.
9.A
解:将三角形各顶点的纵坐标都加上3,横坐标保持不变,所得图形的位置与原图形相比向上平移3个单位;
故选:A.
10.C
解:将点P(﹣2,3)向右平移4个单位长度,再向下平移2个单位长度所得到的点坐标为(﹣2+4,3﹣2),即(2,1).
故选:C.
11.(2,1)
解:由A(-3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(-4,3),
∴B1的坐标为(2,1),
故答案为:(2,1).
12.false.
解:设直线y= -3x向上平移了m个单位,
∴直线的解析式为y= -3x+m,
∵直线false经过点false,
∴b=-3a+m,
∵false
∴b=-3a+6,
∴-3a+m=-3a+6,
∴m=6,
∴直线AB的解析式为y=-3x+6,
故答案为:y=-3x+6.
13.false
解:将点P(2,﹣3)向右平移4个单位长度得点P′,
则点P′的坐标为(6,﹣3).
故答案为:(6,﹣3).
14.3
解:∵A(4,3),点C(5,3),
∴AC=5-4=1,false,
∵false沿AC方向平移AC长度的到false,
∴AC=BF,
∴四边形ABFC为平行四边形,
∴四边形ABFC的高为C点到x轴的距离,
∴false,
故答案为:3.
15.false
解:如图,作点B关于x轴的对称点B',连接AB'交x轴于点P,连接PB,
∵点B关于x轴的对称点为点B',点B的坐标为(4,?1),
∴PB=PB',点B'的坐标为(4,1).
∴PA+PB=PA+PB'=AB'.
由两点之间线段最短可知,此时PA+PB的值最小,
∵AB的长不变,
∴△PAB的周长的最小.
∵A(2,?3),B(4,?1),B'(4,1),
∴AB=false,
AB'=false.
∴△PAB的周长的最小值=PA+PB+AB=AB'+AB=false.
故答案为:false.
16.55
解:根据题意作图:
∵从A点沿北偏东60°的方向走了100米到达点B,从点B沿南偏西10°的方向走了100米到达点C,
∴∠1+∠2=60°,AB=BC=100,
∴∠2=50°,且△ABC是等腰三角形,
∴∠BAC=false=65°,
∴∠5=180°-65°-60°=55°,
∴点C在点A的南偏东55°的方向上.
故答案为:55.
17.(1)答案见解析;(2)(1,y)(false);(3)false.
解:(1)如图,false即为所画.
(2)线段false上任意一点的坐标为(1,y)(false).
(3)取点D(1,-3)、E(3,-1)、F(1,-1),分别连接CD、CE、DF、EF.则四边形CDFE为边长为2的正方形,AF=BF=AE=BD=1、CD=CE=2.
∴false.
18.(1)false;(2)图见解析,false
解:(1)false;
(2)平移后如图所示,false.
19.(1)(-1,0)或(9,0);(2)(0,-false).
解:(1)平面直角坐标系中,点false和false,
OA=3,OB=4,∠AOB=90 ?,
在Rt△AOB中,由勾股定理AB=false ,
以B为圆心,AB长为半径在x轴上截取两点C1、C2,
△ABC1是等腰三角形,AB=BC1=5,OC1=BC1-OB=5-4=1,则C1坐标为(-1,0),
△ABC2是等腰三角形,AB=BC2=5,OC2=BC2+OB=5+4=9,则C1坐标为(9,0),
则C点坐标为(-1,0)或(9,0),
(2)设OD=x,
∠BOD=90?,
在Rt△BOD中BD2=OB2+OD2=16+x2,
由false,
AD=3+x,
由勾股定理AD2=AB2+BD2,
false,
解这个方程得false,
则D点的坐标为(0,-false).
