1.1等腰三角形 随堂小练笔（含答案）

中小学教育资源及组卷应用平台
威宁自治县保家中学
八年级数字
1.1等腰三角形
配套练习
知识梳理
1.______分别相等且其中一组等角的_______相等的两个三角形全等.
2.全等三角形的对应边
，对应角
。
3.等腰三角形的两底角
（简称为
)
4.等腰三角形
、
及
互相重合。
随堂练习
一、选择题
1.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是（
）
A.AC=BD
B.∠CAB=∠DBA
C.∠C=∠D
D.
BC=
AD
2.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD、CE交于点H,已知EH=EB=3,AE=5,则CH的长是（
）
A.2
B.2.5
C.1.5
D.1
3.在△ABC中，AB=AC,若∠A=，则∠C等于多少度（
）
A.
B.
C.
D.
4.下列结论不正确的是（
）
A.等腰三角形底边上的中线与底边上的高相等
B.顶角相等的两个等腰三角形全等
C.等腰三角形顶角的外角是底角的2倍
D.等腰三角形的两底角相等
5.如图，已知：∥，AB=CD，若要使△ABE≌△CDF,仍需添加一个条件，下
列条件中，哪一个不能使△ABE≌△CDF的是（
）
A.∠A=∠B
B.BF=CE
C.AE∥DF
D.AE=DF
6.如图，△ABC≌△BAD.若AB＝6，AC＝4，BC＝5，则AD的长为(
)
A．4　
B．5　　
C．6　
　
　D．以上都不对
7.已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为(
)
A．13
B．17
C．13或17
D．13或10
8.等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（　　）
A．
60°
B．
120°
C．
60°或150°
D．
60°或120°
二、解答题
9.已知如图，△ABC中AB＝AC，点D、E在BC上且AD=AE，求证：BD=CE
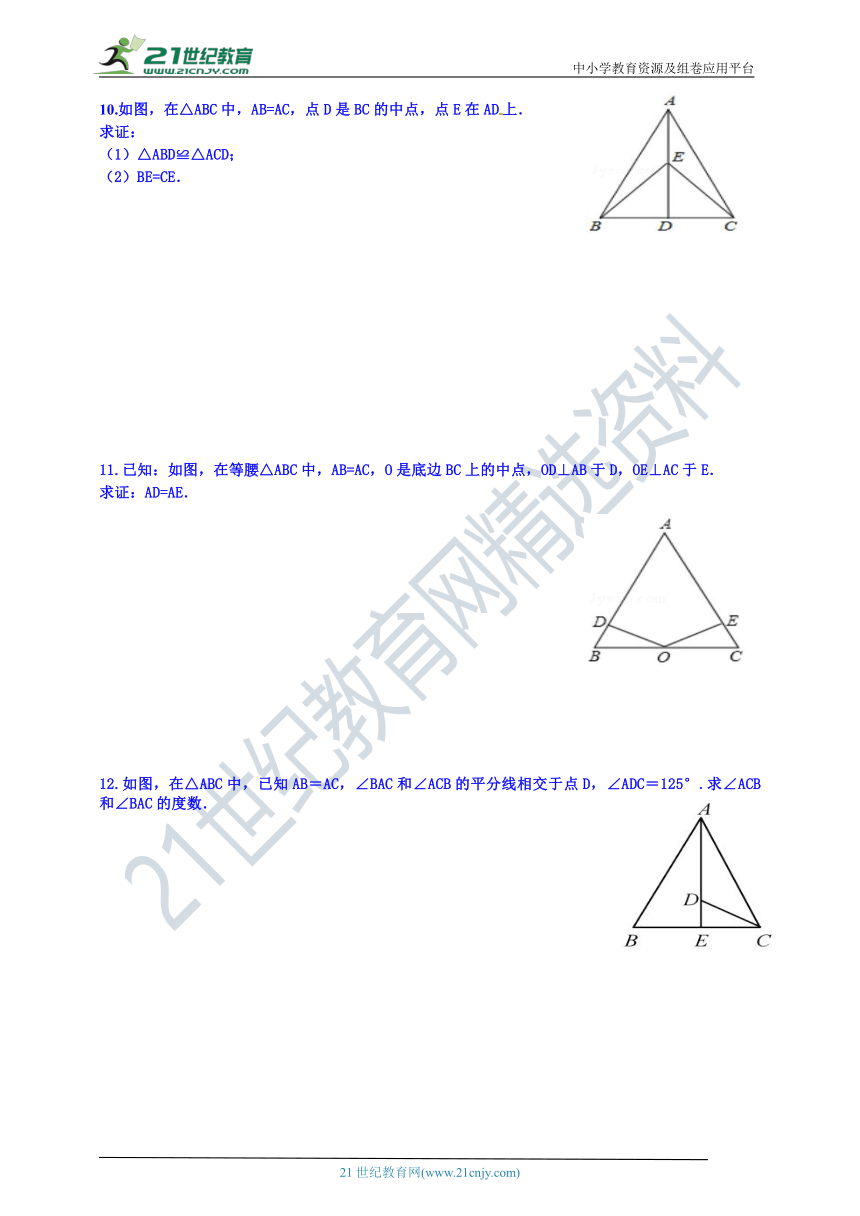
10.如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．
求证：
（1）△ABD≌△ACD；
（2）BE=CE．
11.已知：如图，在等腰△ABC中，AB=AC，O是底边BC上的中点，OD⊥AB于D，OE⊥AC于E．
求证：AD=AE．
12.如图，在△ABC中，已知AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝125°.求∠ACB和∠BAC的度数．
参考答案
知识梳理
两角；对边；
相等；相等；
相等；等边对等角；
顶角的角平分线；底边上的中线；底边上的高；
一、选择题
1.A
2.A
3.A
4.B
5.D
6.B
7.B
8.D
二、解答题
9.证明：作AF⊥BC于F,
∵
AB="AC,"
AF⊥BC于F,
∴
BF=CF
∵
AD="AE,"
AF⊥BC于F,
∴
DF=EF,????????
∴
BF-DF=CF-EF即
BD=CE??
10.证明：（1）∵D是BC的中点，
∴BD=CD，
在△ABD和△ACD中，
，
∴△ABD≌△ACD（SSS）
（2）由（1）知△ABD≌△ACD，
∴∠BAD=∠CAD，即∠BAE=∠CAE，
在△ABE和△ACE中，
∴△ABE≌△ACE
（SAS），
∴BE=CE。
11.证明：∵AB=AC，
∴∠B=∠C．
∵OD⊥AB，OE⊥AC，
∴∠ODB=∠OEC=90°．
∵O是底边BC上的中点，
∴OB=OC，
在△OBD与△OCE中，
∵
∠ODB=∠OEC
∠B=∠C
OB=OC
∴△OBD≌△OCE（AAS）．
∴BD=CE．
∵AB=AC，
∴AB-BD=AC-CE．
即AD=AE。
12.∵AB=AC，AE平分∠BAC，
∴AE⊥BC（等腰三角形三线合一），
∵∠ADC=125°，
∴∠CDE=55°，
∴∠DCE=90°-∠CDE=35°，
又∵CD平分∠ACB，
∴∠ACB=2∠DCE=70°．
又∵AB=AC，
∴∠B=∠ACB=70°，
∴∠BAC=180-（∠B+∠ACB）=40°
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)