【同步备课】北师大四下第二单元认识三角形和四边形单元检测B卷
文档属性
| 名称 | 【同步备课】北师大四下第二单元认识三角形和四边形单元检测B卷 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大四下第二单元认识三角形和四边形单元题
一.选择题(满分16分,每小题2分)
1.在下列长度的四根小棒中,能与、长的两根小棒钉成一个三角形的是
A. B. C.
2.梯形是只有 组对边平行的四边形.
A.0 B.2 C.1
3.下面三根小棒不能围成三角形的是 (单位:厘米)
A.3、6、8 B.5、3、4 C.5、6、12
4.房子的屋顶有很多三角形,其中很重要的原因是利用了三角形的
A.稳定性 B.内角和是180度
C.任意两边之和大于第三边
5.如果一个三角形的两条边分别是4厘米和7厘米,那么另一条边可能是 厘米.
A.2 B.3 C.7
6.图中最有稳定性的图形是
A. B.
C.
7.一个钝角三角形的三个内角中,最多有 个钝角.
A.1 B.2 C.3
8.把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是
A.和 B.和 C.和
二.填空题(满分16分,每小题2分)
9.在能围成三角形的各组小棒后面画“”.
(1)3厘米、5厘米、9厘米 ; (2)6厘米、6厘米、6厘米 ;
(3)5厘米、5厘米、9厘米 ; (4)12厘米、4厘米、8厘米 .
10.三角形_???è§?????????????_ 三角形、 三角形、 三角形.三条边相等的三角形叫做 三角形,又叫做 三角形.等腰三角形的两个底角 .
11.古代的木屋的屋顶架都制成三角形就是应用了三角形的 来设计的.
12.只有一组对边平行的四边形是 .生活中常见的伸缩门、升降机等都是应用了平行四边形 的特点.21·cn·jy·com
13.把一根长15分米的铁丝剪成三段,围成一个三角形,这三段都是整分米数,它们的长度可能分别是 分米、 分米、 分米.【来源:21·世纪·教育·网】
14.找一找如图中,哪些是平行四边形,哪些是梯形,并将序号填在相应的框里.
平行四边形
梯形 .
15.正方形是特殊的 ,长方形是特殊的 ,平行四边形是特殊的 .
16.正方形有 条边,每条边的长度 ,有 个角,每个角都是 角.
三.判断题(满分8分,每小题2分)
17.梯形和平行四边形都具有稳定性. .(判断对错)
18.在平行四边形中,有一个角是直角,这个四边形一定是长方形 .(判断对错)
19.把一个大三角形切成两个小三角形,这两个小三角形各自的内角和都小于 .(判断对错)
20.在钝角三角形中,一个钝角比两个锐角的和大. .(判断对错)
四.操作题(满分24分,每小题6分)
21.(6分)接着画出平行四边形.
22.(6分)标出下列图形中各部分的名称.
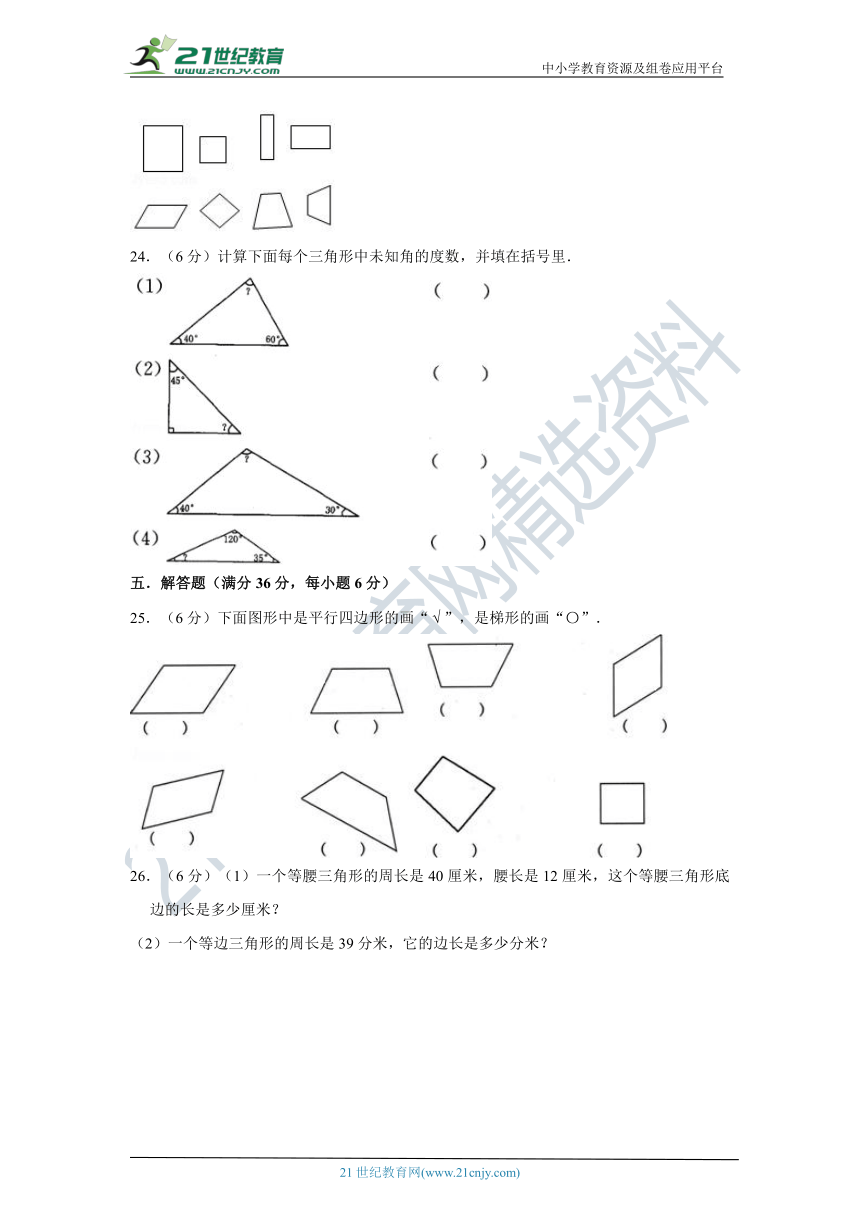
23.(6分)把下面的图形分类(把你认为是一类的用圈圈起来)
24.(6分)计算下面每个三角形中未知角的度数,并填在括号里.
五.解答题(满分36分,每小题6分)
25.(6分)下面图形中是平行四边形的画“”,是梯形的画“〇”.
26.(6分)(1)一个等腰三角形的周长是40厘米,腰长是12厘米,这个等腰三角形底边的长是多少厘米?21cnjy.com
(2)一个等边三角形的周长是39分米,它的边长是多少分米?
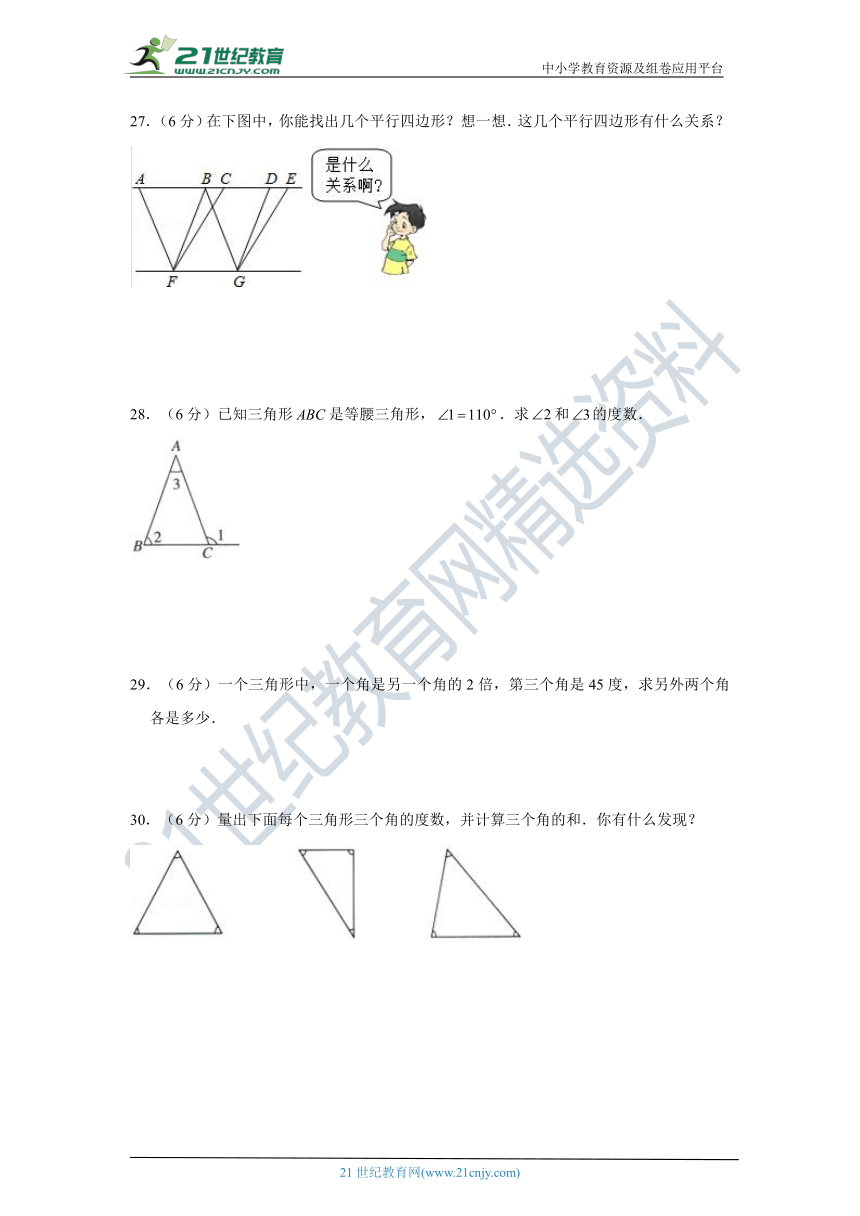
27.(6分)在下图中,你能找出几个平行四边形?想一想.这几个平行四边形有什么关系?
28.(6分)已知三角形是等腰三角形,.求和的度数.
29.(6分)一个三角形中,一个角是另一个角的2倍,第三个角是45度,求另外两个角各是多少.
30.(6分)量出下面每个三角形三个角的度数,并计算三个角的和.你有什么发现?
北师大四下第二单元认识三角形和四边形单元题
参考答案
一.选择题
1.解:
所以第三条线段的长度在厘米之间(不包括5和13厘米),结合选项可知:9厘米符合题意;
答案:.
2.解:梯形是只有一组对边平行的四边形;
答案:.
3.解:、,能围成三角形;
、,所以能围成三角形;
、,所以不能围成三角形;
、,所以能围成三角形;
答案:.
4.解:房子的屋顶有很多三角形,其中很重要的原因是利用了三角形的稳定性.
答案:.
5.解:第三边,
第三边,那么第三边的长度可能是厘米(不包括3厘米和11厘米),
所以第三条边可能是4、5、6、7、8、9、10厘米.
答案:.
6.解:因为在三角形中,任取三角形两条边,则两条边的非公共端点被第三条边连接,第三条边不可伸缩或弯折,因此三角形具有稳定性;21世纪教育网版权所有
而平行四边形、正方形、长方形都不具备这一特点,所以说它们不如三角形稳定;
答案:。
7.解:假设钝角三角形中不只1个钝角,则根据钝角的意义可知,三角形的三个内角的和大于,与三角形内角和定理矛盾,所以一个钝角三角形的三个内角中,最多有1个钝角。21·世纪*教育网
答案:。
8.解:把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是和。
答案:。
二.填空题
9.解:(1)因为厘米,
所以不能拼成三角形;
(2)因为,
所以能拼成三角形;
(3)因为,
所以能拼成三角形.
(4)因为
所以不能拼成三角形.
所以(1)3厘米、5厘米、9厘米; (2)6厘米、6厘米、6厘米;
(3)5厘米、5厘米、9厘米; (4)12厘米、4厘米、8厘米
答案:,,,.
10.解:根据三角形的_????±?????????????_角形按角的大小分可以分为锐角三角形、直角三角形、钝角三角形;三角形按边可以分为等边三角形和等腰三角形,三条边相等的三角形叫做等边三角形,又叫做正三角形.等腰三角形的两个底角相等.21教育网
答案:锐角、钝角、直角、等边、正、相等.
11.解:古代的木屋的屋顶架都制成三角形就是应用了三角形的稳定性来设计的.
答案:稳定性.
12.解:只有一组对边平行的四边形是 梯形.生活中常见的伸缩门、升降机等都是应用了平行四边形 不稳定性的特点.www.21-cn-jy.com
答案:梯形、不稳定性.
13.解:根据三角形的三边关系可知:把一根长15厘米的铁丝剪成7厘米、6厘米、2厘米的三段就能围成一个三角形.2·1·c·n·j·y
答案:7,6,2(答案不唯一).
14.解:④,⑤,⑦是平行四边形,①,③,⑥是梯形;
答案:④,⑤,⑦;①,③,⑥.
15.解:正方形是特殊的长方形,长方形是特殊的平行四边形,平行四边形是特殊的菱形.
答案:长方形、平行四边形、菱形.
16.解:正方形有4条边,每条边的长度都相等,有4个角,每个角都是直角.
答案:4、都相等、4、直角.
三.判断题
17.解:平行四边形具有稳定性,是错误的,它具有不稳定性;
答案:.
18.解:根据长方形和平行四边形的特征,在平行四边形中,有一个角是直角,这个四边形一定是长方形;
答案:.
19.解:根据题干分析可得:把一个大三角形切成两个小三角形,这两个小三角形各自的内角和都等于180度,原题说法错误.www-2-1-cnjy-com
答案:.
20.解:因为三角形的内角和是180度,其中已经有一个角是大于90度的,
所以剩下两个锐角的和小于90度;
所以题干说法正确.
答案:.
四.操作题
21.解:作图如下:
22.解:根据分析可作图如下:
23.解:第一行前两个是正方形,后两个是长方形,
第二行前两个是平行四边形,后两个是梯形,
24.解:(1)
(2)
(3)
(4)
如图:
五.解答题
25.解:分类后如下:
26.解:(1)(厘米);
答:这个等腰三角形底边的长是16厘米.
(2)(分米);
答:它的边长是13分米.
27.解:图中的平行四边形有:,,共3个;
答:图中的平行四边形有:,,共3个,这几个平行四边形等底等高.
28.解:因为,则,
;
答:是,是.
29.解:设一个角的度数为,则另一个角的度数为,
,
,
,
;
答:另外两个角各是、.
30.解:图一:三个角都是60度,内角和是:(度;
图二:三个角分别是90度、60度、30度,所以内角和是:(度;
图三:三个角分别是80度、45度、55度,所以内角和是:(度;
得出:三角形的三个内角的度数之和为.
_21?????????è?????(www.21cnjy.com)_
北师大四下第二单元认识三角形和四边形单元题
一.选择题(满分16分,每小题2分)
1.在下列长度的四根小棒中,能与、长的两根小棒钉成一个三角形的是
A. B. C.
2.梯形是只有 组对边平行的四边形.
A.0 B.2 C.1
3.下面三根小棒不能围成三角形的是 (单位:厘米)
A.3、6、8 B.5、3、4 C.5、6、12
4.房子的屋顶有很多三角形,其中很重要的原因是利用了三角形的
A.稳定性 B.内角和是180度
C.任意两边之和大于第三边
5.如果一个三角形的两条边分别是4厘米和7厘米,那么另一条边可能是 厘米.
A.2 B.3 C.7
6.图中最有稳定性的图形是
A. B.
C.
7.一个钝角三角形的三个内角中,最多有 个钝角.
A.1 B.2 C.3
8.把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是
A.和 B.和 C.和
二.填空题(满分16分,每小题2分)
9.在能围成三角形的各组小棒后面画“”.
(1)3厘米、5厘米、9厘米 ; (2)6厘米、6厘米、6厘米 ;
(3)5厘米、5厘米、9厘米 ; (4)12厘米、4厘米、8厘米 .
10.三角形_???è§?????????????_ 三角形、 三角形、 三角形.三条边相等的三角形叫做 三角形,又叫做 三角形.等腰三角形的两个底角 .
11.古代的木屋的屋顶架都制成三角形就是应用了三角形的 来设计的.
12.只有一组对边平行的四边形是 .生活中常见的伸缩门、升降机等都是应用了平行四边形 的特点.21·cn·jy·com
13.把一根长15分米的铁丝剪成三段,围成一个三角形,这三段都是整分米数,它们的长度可能分别是 分米、 分米、 分米.【来源:21·世纪·教育·网】
14.找一找如图中,哪些是平行四边形,哪些是梯形,并将序号填在相应的框里.
平行四边形
梯形 .
15.正方形是特殊的 ,长方形是特殊的 ,平行四边形是特殊的 .
16.正方形有 条边,每条边的长度 ,有 个角,每个角都是 角.
三.判断题(满分8分,每小题2分)
17.梯形和平行四边形都具有稳定性. .(判断对错)
18.在平行四边形中,有一个角是直角,这个四边形一定是长方形 .(判断对错)
19.把一个大三角形切成两个小三角形,这两个小三角形各自的内角和都小于 .(判断对错)
20.在钝角三角形中,一个钝角比两个锐角的和大. .(判断对错)
四.操作题(满分24分,每小题6分)
21.(6分)接着画出平行四边形.
22.(6分)标出下列图形中各部分的名称.
23.(6分)把下面的图形分类(把你认为是一类的用圈圈起来)
24.(6分)计算下面每个三角形中未知角的度数,并填在括号里.
五.解答题(满分36分,每小题6分)
25.(6分)下面图形中是平行四边形的画“”,是梯形的画“〇”.
26.(6分)(1)一个等腰三角形的周长是40厘米,腰长是12厘米,这个等腰三角形底边的长是多少厘米?21cnjy.com
(2)一个等边三角形的周长是39分米,它的边长是多少分米?
27.(6分)在下图中,你能找出几个平行四边形?想一想.这几个平行四边形有什么关系?
28.(6分)已知三角形是等腰三角形,.求和的度数.
29.(6分)一个三角形中,一个角是另一个角的2倍,第三个角是45度,求另外两个角各是多少.
30.(6分)量出下面每个三角形三个角的度数,并计算三个角的和.你有什么发现?
北师大四下第二单元认识三角形和四边形单元题
参考答案
一.选择题
1.解:
所以第三条线段的长度在厘米之间(不包括5和13厘米),结合选项可知:9厘米符合题意;
答案:.
2.解:梯形是只有一组对边平行的四边形;
答案:.
3.解:、,能围成三角形;
、,所以能围成三角形;
、,所以不能围成三角形;
、,所以能围成三角形;
答案:.
4.解:房子的屋顶有很多三角形,其中很重要的原因是利用了三角形的稳定性.
答案:.
5.解:第三边,
第三边,那么第三边的长度可能是厘米(不包括3厘米和11厘米),
所以第三条边可能是4、5、6、7、8、9、10厘米.
答案:.
6.解:因为在三角形中,任取三角形两条边,则两条边的非公共端点被第三条边连接,第三条边不可伸缩或弯折,因此三角形具有稳定性;21世纪教育网版权所有
而平行四边形、正方形、长方形都不具备这一特点,所以说它们不如三角形稳定;
答案:。
7.解:假设钝角三角形中不只1个钝角,则根据钝角的意义可知,三角形的三个内角的和大于,与三角形内角和定理矛盾,所以一个钝角三角形的三个内角中,最多有1个钝角。21·世纪*教育网
答案:。
8.解:把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是和。
答案:。
二.填空题
9.解:(1)因为厘米,
所以不能拼成三角形;
(2)因为,
所以能拼成三角形;
(3)因为,
所以能拼成三角形.
(4)因为
所以不能拼成三角形.
所以(1)3厘米、5厘米、9厘米; (2)6厘米、6厘米、6厘米;
(3)5厘米、5厘米、9厘米; (4)12厘米、4厘米、8厘米
答案:,,,.
10.解:根据三角形的_????±?????????????_角形按角的大小分可以分为锐角三角形、直角三角形、钝角三角形;三角形按边可以分为等边三角形和等腰三角形,三条边相等的三角形叫做等边三角形,又叫做正三角形.等腰三角形的两个底角相等.21教育网
答案:锐角、钝角、直角、等边、正、相等.
11.解:古代的木屋的屋顶架都制成三角形就是应用了三角形的稳定性来设计的.
答案:稳定性.
12.解:只有一组对边平行的四边形是 梯形.生活中常见的伸缩门、升降机等都是应用了平行四边形 不稳定性的特点.www.21-cn-jy.com
答案:梯形、不稳定性.
13.解:根据三角形的三边关系可知:把一根长15厘米的铁丝剪成7厘米、6厘米、2厘米的三段就能围成一个三角形.2·1·c·n·j·y
答案:7,6,2(答案不唯一).
14.解:④,⑤,⑦是平行四边形,①,③,⑥是梯形;
答案:④,⑤,⑦;①,③,⑥.
15.解:正方形是特殊的长方形,长方形是特殊的平行四边形,平行四边形是特殊的菱形.
答案:长方形、平行四边形、菱形.
16.解:正方形有4条边,每条边的长度都相等,有4个角,每个角都是直角.
答案:4、都相等、4、直角.
三.判断题
17.解:平行四边形具有稳定性,是错误的,它具有不稳定性;
答案:.
18.解:根据长方形和平行四边形的特征,在平行四边形中,有一个角是直角,这个四边形一定是长方形;
答案:.
19.解:根据题干分析可得:把一个大三角形切成两个小三角形,这两个小三角形各自的内角和都等于180度,原题说法错误.www-2-1-cnjy-com
答案:.
20.解:因为三角形的内角和是180度,其中已经有一个角是大于90度的,
所以剩下两个锐角的和小于90度;
所以题干说法正确.
答案:.
四.操作题
21.解:作图如下:
22.解:根据分析可作图如下:
23.解:第一行前两个是正方形,后两个是长方形,
第二行前两个是平行四边形,后两个是梯形,
24.解:(1)
(2)
(3)
(4)
如图:
五.解答题
25.解:分类后如下:
26.解:(1)(厘米);
答:这个等腰三角形底边的长是16厘米.
(2)(分米);
答:它的边长是13分米.
27.解:图中的平行四边形有:,,共3个;
答:图中的平行四边形有:,,共3个,这几个平行四边形等底等高.
28.解:因为,则,
;
答:是,是.
29.解:设一个角的度数为,则另一个角的度数为,
,
,
,
;
答:另外两个角各是、.
30.解:图一:三个角都是60度,内角和是:(度;
图二:三个角分别是90度、60度、30度,所以内角和是:(度;
图三:三个角分别是80度、45度、55度,所以内角和是:(度;
得出:三角形的三个内角的度数之和为.
_21?????????è?????(www.21cnjy.com)_
