苏教版选修2-2第一章导数及其应用复习教案
文档属性
| 名称 | 苏教版选修2-2第一章导数及其应用复习教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 182.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-03 00:00:00 | ||
图片预览





文档简介
本章总结提升
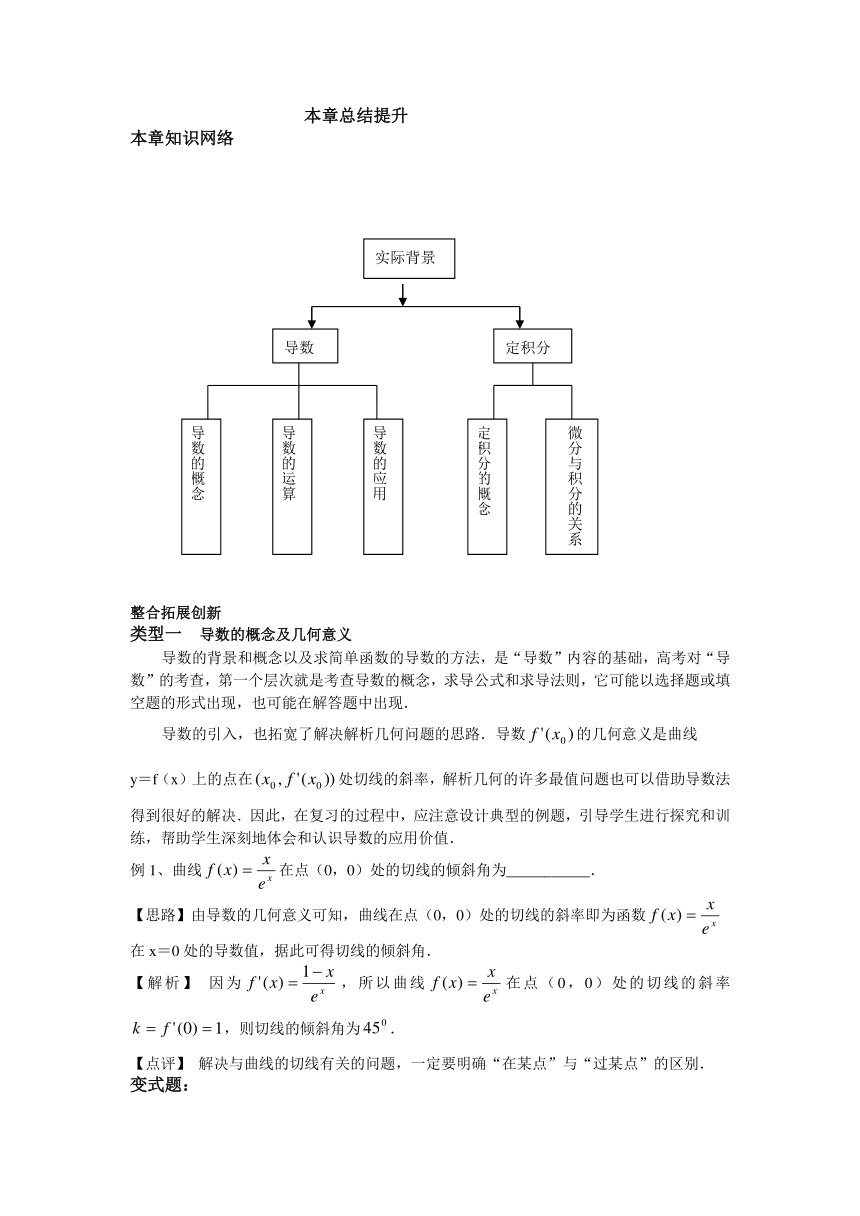
本章知识网络
整合拓展创新
类型一 导数的概念及几何意义
导数的背景和概念以及求简单函数的导数的方法,是“导数”内容的基础,高考对“导
数”的考查,第一个层次就是考查导数的概念,求导公式和求导法则,它可能以选择题或填空题的形式出现,也可能在解答题中出现.
导数的引入,也拓宽了解决解析几何问题的思路.导数的几何意义是曲线
y=f(x)上的点在处切线的斜率,解析几何的许多最值问题也可以借助导数法得到很好的解决.因此,在复习的过程中,应注意设计典型的例题,引导学生进行探究和训练,帮助学生深刻地体会和认识导数的应用价值.
例1、曲线在点(0,0)处的切线的倾斜角为___________.
【思路】由导数的几何意义可知,曲线在点(0,0)处的切线的斜率即为函数
在x=0处的导数值,据此可得切线的倾斜角.
【解析】 因为,所以曲线在点(0,0)处的切线的斜率,则切线的倾斜角为.
【点评】 解决与曲线的切线有关的问题,一定要明确“在某点”与“过某点”的区别.
变式题:
曲线在点处的切线与坐标轴所围三角形的面积是___________.
【答案】
【解析】因为,所以曲线在点处的切线的斜率为,则切线方程为,即,切线与x轴和y轴的交点坐标分别为A(1,0)、,则切线于坐标轴围成的三角形OAB的面积为.
类型二 利用导数的研究函数的单调性、求函数的最值、极值
应用导数研究函数单调性的基本方法,往往涉及分类讨论思想、数形结合思想等,考
查综合应用数学知识解决问题的能力,因此,在复习应用导数求函数单调性的相关问题时,要注意加强对前面章节知识的复习和巩固,强化小综合的应用问题,拓展解决问题的思路.
借助于导数研究函数的极值、最值简洁明快,充分体现了利用导数解题的优越性,是高考考查的一个重要方面.同学们复习时要注意取得极值的条件和求最值的方法.
例2.设,讨论定义在的函数的单调性.
【思路】由于求导后,导函数含有参数,所以如何有条理的分类讨论是解决本题的关键.
【解析】
(1)若,则当时,,单调递减;当时,,单调递增.
(2)若时,则
(ⅰ)若,则当时,,单调递增;当时,,单调递减;当时,,单调递增.
(ⅱ)若,则当时,,单调递减;当时,,单调递增.
(ⅲ)若,则当时, ,单调递减; 当时,,单调递增;当时,,单调递减.
综上所述,当时,的单调增区间是、,单调减区间是;
当时,的单调增区间是,单调减区间是;
当时,的单调增区间是,单调减区间是、.
【点评】导数研究函数的单调性是高考中最常见的考查方式,对函数性质的研究涉及到方方面面,涉及方法思想较多,数形结合思想、分类讨论思想、逆向思维等等.
例3、已知函数在点处取得极小值,其导函数的图象经过(-1,0),(5,0),如图,
求:(1)的值;(2)a,b,c的值.
【思路】本题属于对函数的逆向考查,已知极值求参数问题,对于函数极大(小)值的条件,一定要既考虑,又考虑点左右两侧导函数值的正负.
【解析】
观察图象,我们可发现当或时,,
此时,f(x)为减函数;当时,,此时,f(x)为增函数.列表如下:
x -1 5
- 0 + 0 -
↘ 极小值 ↗ 极大值 ↘
因此,在x=-1处函数取得极小值,结合已知,可得=-1.
(2)由(1)知,即,再结合的图象可知,方程
=0的两根分别为-1,5,那么即,
结合,得a=1,b=-4,c=-5.
【点评】本题将函数的解析式、极值、函数单调性,及二次方程根与系数的关系融为一体,涉及知识点较多,只有细心运算,才能确保结论的正确性.
变式题 函数在x=1时有极值10,则a的值为_________.
【解析】,由于当x=1时函数取得极值10,
故必有……(1),……(2),
联立(1)(2),得a=-3或a=4,但当a=-3时,b=3,
此时,虽有,但由极值定义可知当x=1时函数值不是极值,故a=4.
类型三 导数在实际问题中的应用
能用导数的方法求解科学技术、经济活动以及生产与生活实际中的有关使利润最大、用料最省、效率最高等最优化问题,了解导数在解决实际问题中的作用,是新课程对导数提出的教学要求之一,也是新课程的高考要求考生必须掌握的内容之一.在复习教学中,要注意运用学生熟悉的数学问题以及生产、生活实际中的问题,使学生充分感受导数在解决数学问题和实际问题中的应用,帮助学生增强数学应用的意识.
例4.烟囱向其周围地区散落烟尘造成环境污染. 已知A、B两座烟囱相距20km,其中B烟囱喷出的烟尘量是A烟囱的8倍,经环境检测表明:落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比.(比例系数为k).若C是AB连线上的点,设AC=x km,C点的烟尘浓度记为y.
(Ⅰ)写出y关于x的函数表达式;
(Ⅱ)是否存在这样的点C,使该点的烟尘浓度最低?若存在,求出AC的距离;若不存在,说明理由.
【思路】解决应用问题的关键是建立正确的函数模型,再借助导数的工具作用求解.
【解析】(Ⅰ)不妨设A烟囱喷出的烟尘量为1,则B烟囱喷出的烟尘量为8,由AC=x,,可得BC=20-x;
依题意,点C处的烟尘浓度y的函数表达式为:
,
(Ⅱ)对(Ⅰ)中的函数表达式求导得
;
令,得;
又,∴.
∵当时,;当时,,
∴当时,y取最小值.
故存在点C,当km时,该点的烟尘浓度最低.
【点评】在利用导数解决这类优化问题时,其一般步骤是:(1)设出恰当的未知量,并确定未知量的取值范围(即函数定义域);(2)依题意将所求最值的量表示为未知量的函数;(3)求出函数的导数,令导数等于0,得到导数为0的点;(4)通过单调性确定出函数的最值点以及最值.
变式题:某厂生产某产品x吨的总成本(万元),已知产品单价的平方与产品吨数x成反比,生产100吨这种单价为50万元的产品,产量定为多少时总利润最大?
【解析】设单价为a万元,产品总利润为y万元.则,由,得k=250000,
所以,而y=ax-C(x),即,
得(),则,令,得x=25,
当025时,,此时函数递减.
因此,当x=25时,y有最大值,即产量定为25吨时,总利润最大,其利润为万元.
类型四 导数在方程、不等式中的应用
例5、已知函数 (x>0)在处取得极值,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式恒成立,求c的取值范围.
【思路】(1)由函数在处取得极值,从而得到,进而求得的值;由(1)的结论,利用导数讨论函数的单调区间;(3)对任意x>0,不等式恒成立即是,这样利用导数求得在上的最小值即可.
【解析】(I)由题意知,因此,从而.
又对求导得.
由题意,因此,解得.
(II)由(I)知(),令,解得.
当时,,此时为减函数;
当时,,此时为增函数.
因此的单调递减区间为,而的单调递增区间为.
(III)由(II)知,在处取得极小值,此极小值也是最小值,要使()恒成立,只需.
即,从而,
解得或.
所以的取值范围为.
【点评】本小题主要考查函数的单调性及极值、最值,考查运用导数研究函数单调性及极值、最值等基础知识,考查综合分析和解决问题的能力.求解中利用了恒成立的结论:在[a,b]上恒成立,只须;在[a,b]上恒成立,只须.
变式题: 设函数.
(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若对任意的不等式| f′(x)|≤a恒成立,求a的取值范围.
【解析】(Ⅰ)
令得的单调递增区间为(a,3a)
令得的单调递减区间为(-,a)和(3a,+)
∴当x=a时,极小值=
当x=3a时,极小值=b.
(Ⅱ)由||≤a,得-a≤-x2+4ax-3a2≤a.①
∵0∴a+1>2a.
∴上是减函数.
∴
于是,对任意,不等式①恒成立,等价于
又
∴
高考零距离
1、(2011,广东理12)12.函数在 处取得极小值.
2、(2011,湖南文7).曲线在点处的切线的斜率为( )
A. B. C. D.
答案:B
解析:,所以
。
3、(2011,福建文10).若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于
A.2 B.3 C.6 D.9
答案:D
4.(2011,江苏12).在平面直角坐标系中,已知点P是函数的图象上的动点,该图象在P处的切线交y轴于点M,过点P作的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________
答案:
解析:设则,过点P作的垂线
,
,所以,t在上单调增,在单调减,.
本题主要考查指数运算,指数函数图象、导数的概念,导数公式,导数的运算与几何意义、利用导数研究函数,导数的应用、直线方程及其斜率、直线的位置关系,运算求解能力,综合应用有关知识的能力,本题属难题.
5、(2011,安徽理(16)(本小题满分12分)
设,其中为正实数
(Ⅰ)当时,求的极值点;
(Ⅱ)若为上的单调函数,求的取值范围。
分析:本题考查导数的运算,极值点的判断,导数符号与函数单调变化之间的关系,求解二次不等式,考查运算能力,综合运用知识分析和解决问题的能力.
解:对求导得 ①
(I)当,若
综合①,可知
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
所以,是极小值点,是极大值点.
(II)若为R上的单调函数,则在R上不变号,结合①与条件a>0,知
在R上恒成立,因此由此并结合,知
6.(2011,江苏19).(本小题满分16分)已知a,b是实数,函数 和是的导函数,若在区间I上恒成立,则称和在区间I上单调性一致.
(1)设,若函数和在区间上单调性一致,求实数b的取值范围;
(2)设且,若函数和在以a,b为端点的开区间上单调性一致,求|a-b|的最大值.
答案:
因为函数和在区间上单调性一致,所以,
即
即实数b的取值范围是
由
若,则由,,和在区间上不是单调性一致,
所以.
;又.
所以要使,只有,
取,当时, 因此
当时,因为,函数和在区间(b,a)上单调性一致,所以,
即,
设,考虑点(b,a)的可行域,函数的斜率为1的切线的切
点设为
则;
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即,
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即而x=0时,不符合题意,
当时,由题意:
综上可知,。
解析:本题主要考查单调性概念、导数运算及应用、含参不等式恒成立问题,综合考查、线性规划、解二次不等式、二次函数、化归及数形结合的思想,考查用分类讨论思想进行探索分析和解决问题的综合能力.(1)中档题;(2)难题.
导数
定积分
导数的概念
导数的运算
导数的应用
定积分的概念
微分与积分的关系
实际背景
A
B
·
C
本章知识网络
整合拓展创新
类型一 导数的概念及几何意义
导数的背景和概念以及求简单函数的导数的方法,是“导数”内容的基础,高考对“导
数”的考查,第一个层次就是考查导数的概念,求导公式和求导法则,它可能以选择题或填空题的形式出现,也可能在解答题中出现.
导数的引入,也拓宽了解决解析几何问题的思路.导数的几何意义是曲线
y=f(x)上的点在处切线的斜率,解析几何的许多最值问题也可以借助导数法得到很好的解决.因此,在复习的过程中,应注意设计典型的例题,引导学生进行探究和训练,帮助学生深刻地体会和认识导数的应用价值.
例1、曲线在点(0,0)处的切线的倾斜角为___________.
【思路】由导数的几何意义可知,曲线在点(0,0)处的切线的斜率即为函数
在x=0处的导数值,据此可得切线的倾斜角.
【解析】 因为,所以曲线在点(0,0)处的切线的斜率,则切线的倾斜角为.
【点评】 解决与曲线的切线有关的问题,一定要明确“在某点”与“过某点”的区别.
变式题:
曲线在点处的切线与坐标轴所围三角形的面积是___________.
【答案】
【解析】因为,所以曲线在点处的切线的斜率为,则切线方程为,即,切线与x轴和y轴的交点坐标分别为A(1,0)、,则切线于坐标轴围成的三角形OAB的面积为.
类型二 利用导数的研究函数的单调性、求函数的最值、极值
应用导数研究函数单调性的基本方法,往往涉及分类讨论思想、数形结合思想等,考
查综合应用数学知识解决问题的能力,因此,在复习应用导数求函数单调性的相关问题时,要注意加强对前面章节知识的复习和巩固,强化小综合的应用问题,拓展解决问题的思路.
借助于导数研究函数的极值、最值简洁明快,充分体现了利用导数解题的优越性,是高考考查的一个重要方面.同学们复习时要注意取得极值的条件和求最值的方法.
例2.设,讨论定义在的函数的单调性.
【思路】由于求导后,导函数含有参数,所以如何有条理的分类讨论是解决本题的关键.
【解析】
(1)若,则当时,,单调递减;当时,,单调递增.
(2)若时,则
(ⅰ)若,则当时,,单调递增;当时,,单调递减;当时,,单调递增.
(ⅱ)若,则当时,,单调递减;当时,,单调递增.
(ⅲ)若,则当时, ,单调递减; 当时,,单调递增;当时,,单调递减.
综上所述,当时,的单调增区间是、,单调减区间是;
当时,的单调增区间是,单调减区间是;
当时,的单调增区间是,单调减区间是、.
【点评】导数研究函数的单调性是高考中最常见的考查方式,对函数性质的研究涉及到方方面面,涉及方法思想较多,数形结合思想、分类讨论思想、逆向思维等等.
例3、已知函数在点处取得极小值,其导函数的图象经过(-1,0),(5,0),如图,
求:(1)的值;(2)a,b,c的值.
【思路】本题属于对函数的逆向考查,已知极值求参数问题,对于函数极大(小)值的条件,一定要既考虑,又考虑点左右两侧导函数值的正负.
【解析】
观察图象,我们可发现当或时,,
此时,f(x)为减函数;当时,,此时,f(x)为增函数.列表如下:
x -1 5
- 0 + 0 -
↘ 极小值 ↗ 极大值 ↘
因此,在x=-1处函数取得极小值,结合已知,可得=-1.
(2)由(1)知,即,再结合的图象可知,方程
=0的两根分别为-1,5,那么即,
结合,得a=1,b=-4,c=-5.
【点评】本题将函数的解析式、极值、函数单调性,及二次方程根与系数的关系融为一体,涉及知识点较多,只有细心运算,才能确保结论的正确性.
变式题 函数在x=1时有极值10,则a的值为_________.
【解析】,由于当x=1时函数取得极值10,
故必有……(1),……(2),
联立(1)(2),得a=-3或a=4,但当a=-3时,b=3,
此时,虽有,但由极值定义可知当x=1时函数值不是极值,故a=4.
类型三 导数在实际问题中的应用
能用导数的方法求解科学技术、经济活动以及生产与生活实际中的有关使利润最大、用料最省、效率最高等最优化问题,了解导数在解决实际问题中的作用,是新课程对导数提出的教学要求之一,也是新课程的高考要求考生必须掌握的内容之一.在复习教学中,要注意运用学生熟悉的数学问题以及生产、生活实际中的问题,使学生充分感受导数在解决数学问题和实际问题中的应用,帮助学生增强数学应用的意识.
例4.烟囱向其周围地区散落烟尘造成环境污染. 已知A、B两座烟囱相距20km,其中B烟囱喷出的烟尘量是A烟囱的8倍,经环境检测表明:落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比,而与烟囱喷出的烟尘量成正比.(比例系数为k).若C是AB连线上的点,设AC=x km,C点的烟尘浓度记为y.
(Ⅰ)写出y关于x的函数表达式;
(Ⅱ)是否存在这样的点C,使该点的烟尘浓度最低?若存在,求出AC的距离;若不存在,说明理由.
【思路】解决应用问题的关键是建立正确的函数模型,再借助导数的工具作用求解.
【解析】(Ⅰ)不妨设A烟囱喷出的烟尘量为1,则B烟囱喷出的烟尘量为8,由AC=x,,可得BC=20-x;
依题意,点C处的烟尘浓度y的函数表达式为:
,
(Ⅱ)对(Ⅰ)中的函数表达式求导得
;
令,得;
又,∴.
∵当时,;当时,,
∴当时,y取最小值.
故存在点C,当km时,该点的烟尘浓度最低.
【点评】在利用导数解决这类优化问题时,其一般步骤是:(1)设出恰当的未知量,并确定未知量的取值范围(即函数定义域);(2)依题意将所求最值的量表示为未知量的函数;(3)求出函数的导数,令导数等于0,得到导数为0的点;(4)通过单调性确定出函数的最值点以及最值.
变式题:某厂生产某产品x吨的总成本(万元),已知产品单价的平方与产品吨数x成反比,生产100吨这种单价为50万元的产品,产量定为多少时总利润最大?
【解析】设单价为a万元,产品总利润为y万元.则,由,得k=250000,
所以,而y=ax-C(x),即,
得(),则,令,得x=25,
当0
因此,当x=25时,y有最大值,即产量定为25吨时,总利润最大,其利润为万元.
类型四 导数在方程、不等式中的应用
例5、已知函数 (x>0)在处取得极值,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式恒成立,求c的取值范围.
【思路】(1)由函数在处取得极值,从而得到,进而求得的值;由(1)的结论,利用导数讨论函数的单调区间;(3)对任意x>0,不等式恒成立即是,这样利用导数求得在上的最小值即可.
【解析】(I)由题意知,因此,从而.
又对求导得.
由题意,因此,解得.
(II)由(I)知(),令,解得.
当时,,此时为减函数;
当时,,此时为增函数.
因此的单调递减区间为,而的单调递增区间为.
(III)由(II)知,在处取得极小值,此极小值也是最小值,要使()恒成立,只需.
即,从而,
解得或.
所以的取值范围为.
【点评】本小题主要考查函数的单调性及极值、最值,考查运用导数研究函数单调性及极值、最值等基础知识,考查综合分析和解决问题的能力.求解中利用了恒成立的结论:在[a,b]上恒成立,只须;在[a,b]上恒成立,只须.
变式题: 设函数.
(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若对任意的不等式| f′(x)|≤a恒成立,求a的取值范围.
【解析】(Ⅰ)
令得的单调递增区间为(a,3a)
令得的单调递减区间为(-,a)和(3a,+)
∴当x=a时,极小值=
当x=3a时,极小值=b.
(Ⅱ)由||≤a,得-a≤-x2+4ax-3a2≤a.①
∵0
∴上是减函数.
∴
于是,对任意,不等式①恒成立,等价于
又
∴
高考零距离
1、(2011,广东理12)12.函数在 处取得极小值.
2、(2011,湖南文7).曲线在点处的切线的斜率为( )
A. B. C. D.
答案:B
解析:,所以
。
3、(2011,福建文10).若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于
A.2 B.3 C.6 D.9
答案:D
4.(2011,江苏12).在平面直角坐标系中,已知点P是函数的图象上的动点,该图象在P处的切线交y轴于点M,过点P作的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________
答案:
解析:设则,过点P作的垂线
,
,所以,t在上单调增,在单调减,.
本题主要考查指数运算,指数函数图象、导数的概念,导数公式,导数的运算与几何意义、利用导数研究函数,导数的应用、直线方程及其斜率、直线的位置关系,运算求解能力,综合应用有关知识的能力,本题属难题.
5、(2011,安徽理(16)(本小题满分12分)
设,其中为正实数
(Ⅰ)当时,求的极值点;
(Ⅱ)若为上的单调函数,求的取值范围。
分析:本题考查导数的运算,极值点的判断,导数符号与函数单调变化之间的关系,求解二次不等式,考查运算能力,综合运用知识分析和解决问题的能力.
解:对求导得 ①
(I)当,若
综合①,可知
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗
所以,是极小值点,是极大值点.
(II)若为R上的单调函数,则在R上不变号,结合①与条件a>0,知
在R上恒成立,因此由此并结合,知
6.(2011,江苏19).(本小题满分16分)已知a,b是实数,函数 和是的导函数,若在区间I上恒成立,则称和在区间I上单调性一致.
(1)设,若函数和在区间上单调性一致,求实数b的取值范围;
(2)设且,若函数和在以a,b为端点的开区间上单调性一致,求|a-b|的最大值.
答案:
因为函数和在区间上单调性一致,所以,
即
即实数b的取值范围是
由
若,则由,,和在区间上不是单调性一致,
所以.
;又.
所以要使,只有,
取,当时, 因此
当时,因为,函数和在区间(b,a)上单调性一致,所以,
即,
设,考虑点(b,a)的可行域,函数的斜率为1的切线的切
点设为
则;
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即,
当时,因为,函数和在区间(a, b)上单调性一致,所以,
即而x=0时,不符合题意,
当时,由题意:
综上可知,。
解析:本题主要考查单调性概念、导数运算及应用、含参不等式恒成立问题,综合考查、线性规划、解二次不等式、二次函数、化归及数形结合的思想,考查用分类讨论思想进行探索分析和解决问题的综合能力.(1)中档题;(2)难题.
导数
定积分
导数的概念
导数的运算
导数的应用
定积分的概念
微分与积分的关系
实际背景
A
B
·
C
