八年级数学春季专题一 勾股定理与逆定理拓展 学案
文档属性
| 名称 | 八年级数学春季专题一 勾股定理与逆定理拓展 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 530.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021春八年级数学专题讲义
专题一
勾股定理与逆定理的思维提升
一、勾股定理中的常考题型
题型1
利用勾股定理求三角形中的边角问题
【例1】如图,已知E是矩形ABCD一边AD的中点,延长AB至点F连接CE,EF,CF,得到△CEF.且CD=1,AF=2,CF=3.
求CE的长.
【例2】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,
请直接写出BP的长.
题型2
利用勾股定理中的方程思维求线段长
【例3】如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,求DE的长.
题型3
利用勾股定理解决实际问题
【例4】(古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
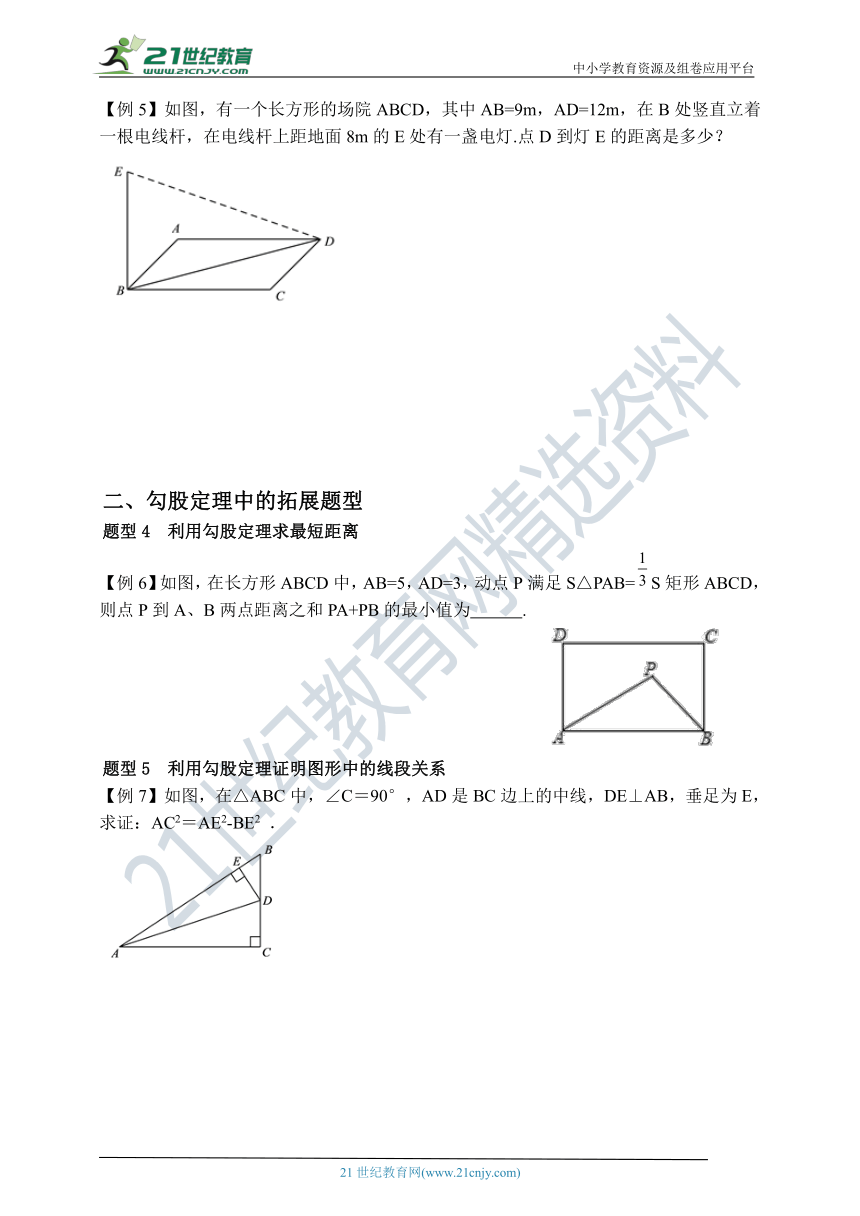
【例5】如图,有一个长方形的场院ABCD,其中AB=9m,AD=12m,在B处竖直立着一根电线杆,在电线杆上距地面8m的E处有一盏电灯.点D到灯E的距离是多少?
二、勾股定理中的拓展题型
题型4
利用勾股定理求最短距离
【例6】如图,在长方形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为
.
题型5
利用勾股定理证明图形中的线段关系
【例7】如图,在△ABC中,∠C=90°,AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2
.
题型6
利用勾股定理求动点中的线段长
【例8】如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
题型7
利用勾股定理解三角形中的综合图形问题
【例9】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB,BC与点D,E,AP平分∠BAC,与DE的延长线交于点P.
(1)求PD的长度;
(2)连接PC,求PC的长度.
【例10】已知正方形ABCD中AC与BD交于点O,点M在线段BD上,作直线AM交直线DC于点E,过D作DH⊥AE于H,设直线DH交AC于点N.
(1)如图1,当M在线段BO上时,求证:OM=ON;
(2)如图2,当M在线段OD上,连接NE和MN,当ENBD时,求证:四边形DENM是菱形;
(3)在(2)的条件下,若正方形边长为4,求EC的长.
【配题练习】
1.将一根的筷子,置于底面直径为,高的圆柱形水杯中,
如图所示,设筷子露在杯子外面的长度,则的取值范围是(???
)
A.????????????????????
B.????????????????????
C.????????????
D.?
2.如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为________.
第2题图
第3题图
第4题图
3.如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,且AH:AE=3:4,那么AH等于
.
4.如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为
.
5.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为
.
6.如图,四边形ABCD中AB=BC=1,CD=,AD=1,且∠B=90°.试求∠BAD的度数.
7.如图,在长方形ABCD中,AB=3,BC=5,在CD上取一点E,连结BE.将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,求CE的长.
8.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
9.图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,
∠ACB=15°,AC=40cm,求支架BC的长.(结果精确到1cm,参考数据:
,
,
)
??????
10.意大利著名画家达?芬奇用如图所示的方法证明了勾股定理,其中左图的空白部分是由两个正方形和两个直角三角形组成,右图的空白部分由两个直角三角形和一个正方形组成.设左图中空白部分的面积为S1,右图中空白部分的面积为S2
.
(1)请用含a,b,c的代数式分别表示S1,S2;
(2)请利用达?芬奇的方法证明勾股定理.
答案解析部分
一、勾股定理中的常考题型
【例1】【答案】
解:
四边形
是矩形,
,
,
,
,,
中,
,
,
,
根据勾股定理得
,
,
∴矩形
中,
,
是
的中点,
,
中,
,
,
,
根据勾股定理得,
.
【例2】【答案】
(1)证明:
∵AD⊥BC,AD=4,BD=2,CD=8,
∴
在Rt△ABD中,由勾股定理得:AB2=AD2+BD2=20.
同理可得:
AC2=CD2+AD2=80.
∵BC=CD+BD=10,
∴BC2=100.
∴AC2+AB2=100=BC2.
∴△ABC是直角三角形.
∴∠BAC=90°.
(2)解:若
为等腰三角形,BP的长可从以下三种情况进行计算:
①当BP=AB时,
∵AD⊥BC,
∴AB=
,
∴BP=AB=
;
②当BP=AP时,
∵△ABC是直角三角形,
∴
∠B+∠C=90°,∠BAP+∠PAC=90°.
∵∠B=∠BAP,
∴∠C=∠PAC.
∴AP=PC.
∴BP=
BC=5.
③当AP=AB时,
∵AD⊥BC,∴
BP=2BD=4.
综上所述:BP的长为
或5或4.
【分析】(1)先利用勾股定理算出AB2及AC2,根据
AC2+AB2=100=BC2利用勾股定理的逆定理进行判定即可;(2)
若为等腰三角形,分三种情况:①当BP=AB时,②当BP=AP时,③当AP=AB时,据此分别解答即可.
【例3】【答案】
解:如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
∵
,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6﹣x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:(6﹣x)2+9=(x+3)2
,
解得x=2.
则DE=2.
【例4】【答案】
解:设水深x尺,则荷花茎的长度为x+0.5,
根据勾股定理得:(x+0.5)2=x2+4
解得:x=3.75.
答:湖水深3.75尺.
【例5】【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
在Rt△BAD中,∠BAD=90°,BD=
=
=15米,
在Rt△EBD中,∠EBD=90°,ED=
=
=17米.
故点D到灯E的距离是17米.
二、勾股定理中的拓展题型
【例6】
【例7】【答案】
证明:∵
∵AD是BC边上的中线,∴BD=CD,∴
,
∵DE⊥AB,∴
,
∴
,
∴
.
【例8】
【例9】
【例10】【答案】
(1)证明:∵DH⊥AE,
∴∠DHA=90°,
∴∠NAH+∠ANH=90°,
∵∠ODN+∠DNO=90°,∠ANH=∠DNO,
∴∠ODN=∠NAH,
在
和
中,
?,
∴
(AAS),
∴OM=ON;
(2)证明:
正方形
,
?
?
由(1)可知,
,
∴OM=ON,
∴∠NMO=45°=∠CDO,
∴ED∥NM,
∵EN∥DM,
∴四边形DENM是平行四边形,
∵DN⊥AE,
∴平行四边形DENM是菱形;
(3)解:∵四边形ABCD为正方形,AD=4,
∴AC=
,
∵四边形DENM是菱形,
∴AH是DN的垂直平分线,
∴AN=AD=4,
∴NC=
,
∵EN∥DM,
∴∠ENC=∠DOC=90°,
∵∠ECN=45°,
∴EC=
.
【配题练习】
1.【答案】
D
2.【答案】
3.【答案】
6
4.【答案】
135
5.【答案】
10
6.【答案】
135°
7.【答案】
8.【答案】解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
9.【答案】
解:过点C作CD⊥MN,垂足为D,
∵∠MAC=60°,∠ACB=15°,
∴∠ABC=60°-15°=45°,∠ACD=30°,
∴△BCD是等腰直角三角形,
∵AC=40cm,
∴在Rt△ACD中,AD=
AC=20cm,
∴CD=
cm,
∴在Rt△BCD中,BC=
cm,
∴支架BC的长为49cm.
10.【答案】
(1)解:
?
(2)解:由
?得
?
?所以
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2021春八年级数学专题讲义
专题一
勾股定理与逆定理的思维提升
一、勾股定理中的常考题型
题型1
利用勾股定理求三角形中的边角问题
【例1】如图,已知E是矩形ABCD一边AD的中点,延长AB至点F连接CE,EF,CF,得到△CEF.且CD=1,AF=2,CF=3.
求CE的长.
【例2】如图,在△ABC中,AD⊥BC,垂足为D,AD=4,BD=2,CD=8.
(1)求证:∠BAC=90°;
(2)P为BC边上一点,连接AP,若△ABP为等腰三角形,
请直接写出BP的长.
题型2
利用勾股定理中的方程思维求线段长
【例3】如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,求DE的长.
题型3
利用勾股定理解决实际问题
【例4】(古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
【例5】如图,有一个长方形的场院ABCD,其中AB=9m,AD=12m,在B处竖直立着一根电线杆,在电线杆上距地面8m的E处有一盏电灯.点D到灯E的距离是多少?
二、勾股定理中的拓展题型
题型4
利用勾股定理求最短距离
【例6】如图,在长方形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为
.
题型5
利用勾股定理证明图形中的线段关系
【例7】如图,在△ABC中,∠C=90°,AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2
.
题型6
利用勾股定理求动点中的线段长
【例8】如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
题型7
利用勾股定理解三角形中的综合图形问题
【例9】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,DE垂直平分AB,分别交AB,BC与点D,E,AP平分∠BAC,与DE的延长线交于点P.
(1)求PD的长度;
(2)连接PC,求PC的长度.
【例10】已知正方形ABCD中AC与BD交于点O,点M在线段BD上,作直线AM交直线DC于点E,过D作DH⊥AE于H,设直线DH交AC于点N.
(1)如图1,当M在线段BO上时,求证:OM=ON;
(2)如图2,当M在线段OD上,连接NE和MN,当ENBD时,求证:四边形DENM是菱形;
(3)在(2)的条件下,若正方形边长为4,求EC的长.
【配题练习】
1.将一根的筷子,置于底面直径为,高的圆柱形水杯中,
如图所示,设筷子露在杯子外面的长度,则的取值范围是(???
)
A.????????????????????
B.????????????????????
C.????????????
D.?
2.如图,有一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10,如图,在OA上取一点E,将△EOC沿EC折叠,使O点落在AB边上的D点处,则点E的坐标为________.
第2题图
第3题图
第4题图
3.如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,且AH:AE=3:4,那么AH等于
.
4.如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为
.
5.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为
.
6.如图,四边形ABCD中AB=BC=1,CD=,AD=1,且∠B=90°.试求∠BAD的度数.
7.如图,在长方形ABCD中,AB=3,BC=5,在CD上取一点E,连结BE.将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,求CE的长.
8.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
9.图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,
∠ACB=15°,AC=40cm,求支架BC的长.(结果精确到1cm,参考数据:
,
,
)
??????
10.意大利著名画家达?芬奇用如图所示的方法证明了勾股定理,其中左图的空白部分是由两个正方形和两个直角三角形组成,右图的空白部分由两个直角三角形和一个正方形组成.设左图中空白部分的面积为S1,右图中空白部分的面积为S2
.
(1)请用含a,b,c的代数式分别表示S1,S2;
(2)请利用达?芬奇的方法证明勾股定理.
答案解析部分
一、勾股定理中的常考题型
【例1】【答案】
解:
四边形
是矩形,
,
,
,
,,
中,
,
,
,
根据勾股定理得
,
,
∴矩形
中,
,
是
的中点,
,
中,
,
,
,
根据勾股定理得,
.
【例2】【答案】
(1)证明:
∵AD⊥BC,AD=4,BD=2,CD=8,
∴
在Rt△ABD中,由勾股定理得:AB2=AD2+BD2=20.
同理可得:
AC2=CD2+AD2=80.
∵BC=CD+BD=10,
∴BC2=100.
∴AC2+AB2=100=BC2.
∴△ABC是直角三角形.
∴∠BAC=90°.
(2)解:若
为等腰三角形,BP的长可从以下三种情况进行计算:
①当BP=AB时,
∵AD⊥BC,
∴AB=
,
∴BP=AB=
;
②当BP=AP时,
∵△ABC是直角三角形,
∴
∠B+∠C=90°,∠BAP+∠PAC=90°.
∵∠B=∠BAP,
∴∠C=∠PAC.
∴AP=PC.
∴BP=
BC=5.
③当AP=AB时,
∵AD⊥BC,∴
BP=2BD=4.
综上所述:BP的长为
或5或4.
【分析】(1)先利用勾股定理算出AB2及AC2,根据
AC2+AB2=100=BC2利用勾股定理的逆定理进行判定即可;(2)
若为等腰三角形,分三种情况:①当BP=AB时,②当BP=AP时,③当AP=AB时,据此分别解答即可.
【例3】【答案】
解:如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
∵
,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6﹣x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:(6﹣x)2+9=(x+3)2
,
解得x=2.
则DE=2.
【例4】【答案】
解:设水深x尺,则荷花茎的长度为x+0.5,
根据勾股定理得:(x+0.5)2=x2+4
解得:x=3.75.
答:湖水深3.75尺.
【例5】【答案】
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
在Rt△BAD中,∠BAD=90°,BD=
=
=15米,
在Rt△EBD中,∠EBD=90°,ED=
=
=17米.
故点D到灯E的距离是17米.
二、勾股定理中的拓展题型
【例6】
【例7】【答案】
证明:∵
∵AD是BC边上的中线,∴BD=CD,∴
,
∵DE⊥AB,∴
,
∴
,
∴
.
【例8】
【例9】
【例10】【答案】
(1)证明:∵DH⊥AE,
∴∠DHA=90°,
∴∠NAH+∠ANH=90°,
∵∠ODN+∠DNO=90°,∠ANH=∠DNO,
∴∠ODN=∠NAH,
在
和
中,
?,
∴
(AAS),
∴OM=ON;
(2)证明:
正方形
,
?
?
由(1)可知,
,
∴OM=ON,
∴∠NMO=45°=∠CDO,
∴ED∥NM,
∵EN∥DM,
∴四边形DENM是平行四边形,
∵DN⊥AE,
∴平行四边形DENM是菱形;
(3)解:∵四边形ABCD为正方形,AD=4,
∴AC=
,
∵四边形DENM是菱形,
∴AH是DN的垂直平分线,
∴AN=AD=4,
∴NC=
,
∵EN∥DM,
∴∠ENC=∠DOC=90°,
∵∠ECN=45°,
∴EC=
.
【配题练习】
1.【答案】
D
2.【答案】
3.【答案】
6
4.【答案】
135
5.【答案】
10
6.【答案】
135°
7.【答案】
8.【答案】解:由题意,AB=15,AC=DE=9,CD=AE=2,BD⊥AC,
在Rt△ACB中,由勾股定理得:
,
∴BD=BC+CD=14(米),
答:发生火灾的住户窗口距离地面14米.
9.【答案】
解:过点C作CD⊥MN,垂足为D,
∵∠MAC=60°,∠ACB=15°,
∴∠ABC=60°-15°=45°,∠ACD=30°,
∴△BCD是等腰直角三角形,
∵AC=40cm,
∴在Rt△ACD中,AD=
AC=20cm,
∴CD=
cm,
∴在Rt△BCD中,BC=
cm,
∴支架BC的长为49cm.
10.【答案】
(1)解:
?
(2)解:由
?得
?
?所以
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
