北师大版八年级数学下册1.1 等腰三角形课件(第3课时 30张)
文档属性
| 名称 | 北师大版八年级数学下册1.1 等腰三角形课件(第3课时 30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 415.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 20:59:50 | ||
图片预览







文档简介
1.1 等腰三角形
(第3课时)
北师大版 八年级 数学 下册
1、问题1:等腰三角形有哪些性质定理及推论?
等腰三角形的两底角相等(简写成 ‘‘等边对等角”).
等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(简写成 ‘‘三线合一”)
问题2:等腰三角形的“等边对等角”的题设和结论分别是什么?
题设:一个三角形是等腰三角形
结论:相等的两边所对应的角相等
导入新知
它的逆命题成立吗?
导入新知
2、思考:如图,在△ABC中,如果∠B
=∠C,那么AB与AC之间有什么关系吗?
3cm
3cm
测量后发现AB与AC相等.
1. 掌握等腰三角形的判定定理及其运用.
2. 理解并掌握反证法的思想,能够运用反证法进行证明.
素养目标
等腰三角形性质定理:______________.
思考:我们把性质定理的条件和结论反过来还成立吗?
即:如果一个三角形有两个角相等,那么这个三角形是等腰三角形吗?
等边对等角
C
B
A
探究新知
知识点 1
等腰三角形的判定
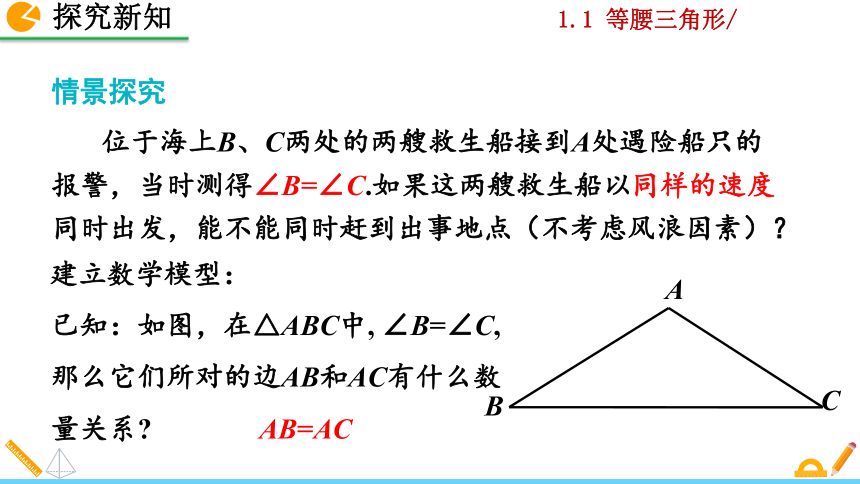
位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
探究新知
情景探究
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
建立数学模型:
C
A
B
AB=AC
做一做:画一个△ABC,其中∠B=∠C=30°.
请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
AB=AC
你能验证你的结论吗?
探究新知
探究新知
已知:
求证:
AB=AC.
如图, 在△ABC中, ∠B=∠C.
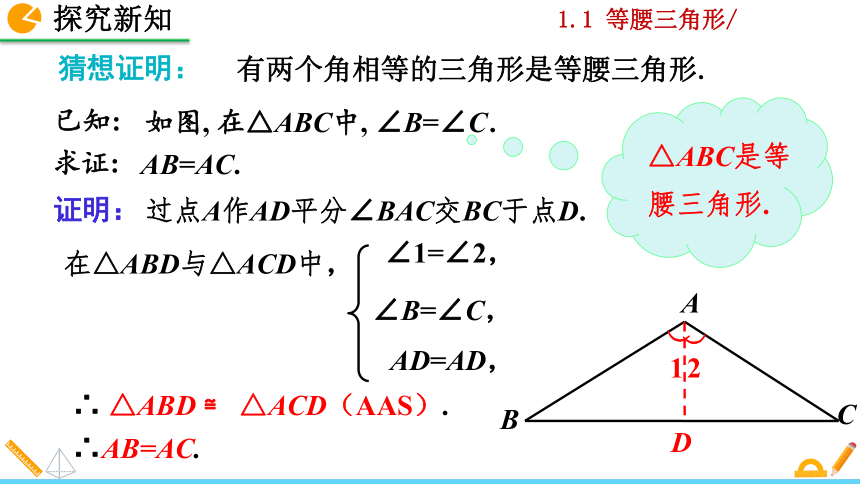
猜想证明:
有两个角相等的三角形是等腰三角形.
在△ABD与△ACD中,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过点A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
△ABC是等腰三角形.
有两个角相等的三角形是等腰三角形.
简述为:“等角对等边”
结论
探究新知
等腰三角形的判定定理:
在△ABC中,
∵∠B=∠C,
应用格式:
∴AB=AC(等角对等边).
A
C
B
A
B
C
D
2
1
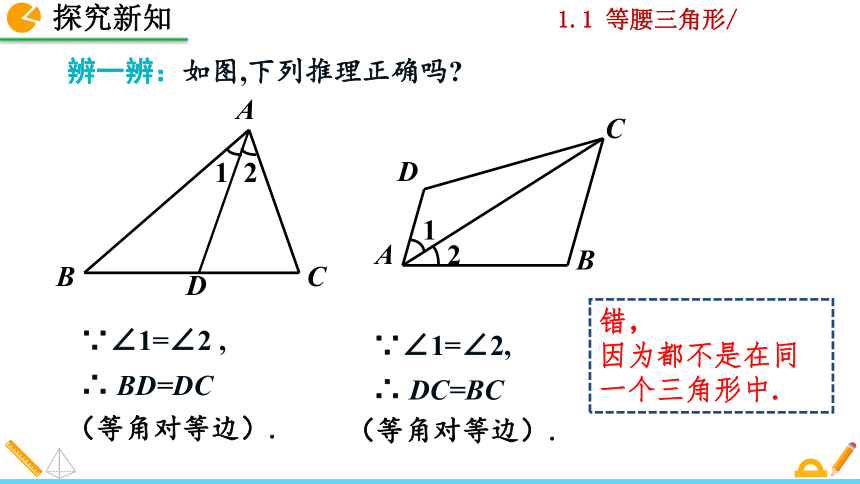
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,
因为都不是在同一个三角形中.
辨一辨:如图,下列推理正确吗?
探究新知
等腰三角形的判定
素养考点 1
探究新知
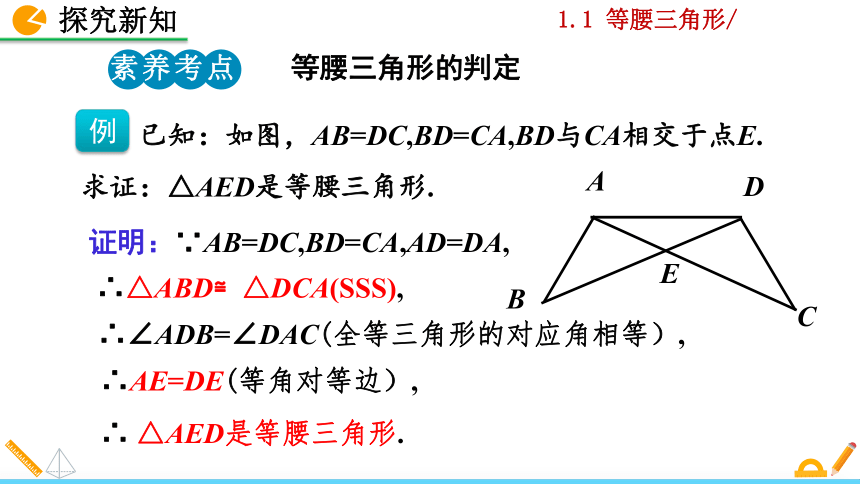
例
已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
巩固练习
变式训练
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4 cm,则CD等于 ( )
A.3 cm B.4 cm
C.1.5 cm D.2 cm
B
如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE相交于点O,给出四个条件:
①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.
上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
A.2种 B.3种 C.4种 D.6种
C
巩固练习
变式训练
探究新知
知识点 2
反证法
想一想:小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
即在△ABC中, 如果∠B≠∠C,那么AB≠AC.
A
B
C
探究新知
C
A
B
如图,在△ABC中,已知∠B≠∠C,
此时, AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等边对等角”定理可得∠B=∠C,
但已知条件是 ∠B≠∠C,“∠B=∠C”与“∠B≠∠C”相矛盾,因此AB≠AC.
小明是这样想的:
你能理解他的推理过程吗?
利用了“反证法”
探究新知
结论
在证明时,先假设命题的结论不成立,然后由此推导出与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
探究新知
①假设: 先假设命题的结论不成立;
②归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
③结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
用反证法证题的一般步骤:
用反证法证明:一个三角形中不能有两个角是直角.
证明:假设∠A、∠B、∠C中有两个角是直角,
不妨设∠A和∠B是直角,即∠A=90°,∠B=90°.
则∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,
所以“∠A和∠B是直角”的假设不成立.
所以一个三角形中不能有两个角是直角.
反证法
素养考点 2
例
探究新知
已知:△ABC.
求证:∠A、∠B、∠C中不能有两个角是直角.
巩固练习
变式训练
用反证法证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
已知:如图,直线l1,l2被l3所截,∠1+∠2=180°.
求证:l1∥l2.
证明:假设l1不平行于l2,即l1与l2相交于一点P.
则∠1+∠2+∠P=180°, 所以∠1+∠2<180°,
这与已知矛盾,故假设不成立.
所以l1∥l2.
巩固练习
变式训练
1.用反证法证明“a>b”时,应假设 ( )
A. a2.用反证法证明命题“四边形的四个内角中至少有一个角大于等于90°”,我们应该假设 ( )
A.四个角都小于90°
B.最多有一个角大于或等于90°
C.有两个角小于90°
D.四个角都大于或等于90°
B
A
连接中考
(2020·南充)如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= ( )
A. B.
C. a-b D. b-a
C
E
2
1
A
B
C
D
72°
36°
③如果AD=4cm,则
1.已知:如图,∠A=36°,
∠DBC=36°,∠C=72°,
①∠1= , ∠2= ;
②图中有 个等腰三角形;
BC= cm;
72°
36°
3
4
个等腰三角形.
④如果过点D作DE∥BC,
交AB于点E,则图中有
5
课堂检测
基础巩固题
2.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,
下列条件中,不能判定△ABC是等腰三角形的是( )
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
D
课堂检测
基础巩固题
3、如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=
∠DBC=36°,则图中等腰三角形的个数是 ( )
A.2 B.3
C.4 D.5
D
课堂检测
基础巩固题
4、如图,在平面直角坐标系中,点B,A分别在x轴,y轴上,
∠BAO=60°,在坐标轴上找一点P,使得△ABP是等腰三
角形,则符合条件的等腰三角形ABP有______个.?
6
课堂检测
基础巩固题
5、如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E.求证:BD+EC=DE.
证明:∵BF平分∠ABC,∴∠1=∠2,
又DE∥BC,∴∠2=∠3,
∴∠1=∠3,
∴DB=DF(等角对等边),
同理可得:EC=EF,
∵DF+EF=DE,
∴BD+EC=DE.
课堂检测
基础巩固题
1、已知如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:AD垂直平分EF.
证明:∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∴∠1=∠2,
易得∠AED=∠AFD=90°,∴∠3=∠4,
∴AE=AF,
∵AD是等腰△AEF的顶角平分线,
∴AD垂直平分EF.
课堂检测
能力提升题
2、如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
证明:∵DE∥AC,∴∠CAD=∠EDA,
∵AD平分∠BAC,∴∠CAD=∠EAD,
∴∠EAD=∠EDA,
∵AD⊥BD,∴∠EAD+∠B=90°,∠EDA+∠BDE=90°,
∴∠B=∠BDE,∴△BDE是等腰三角形.
课堂检测
能力提升题
如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.
求证:△AEF是等腰三角形.
证明:∵FD∥AC,∴∠PFD=∠E,∠FDB= ∠C,
∵AB=AC,∴ ∠B = ∠C,∴∠FDB=∠B,∴FB=FD,
∵FB=FD,EP⊥BC,∴∠PFB=∠PFD,
∵∠PFB=∠AFE,∴∠PFD=∠AFE,
∵∠PFD=∠E,∴∠E=∠AFE, ∴AE=AF, ?
即△AEF是等腰三角形.
课堂检测
拓广探索题
课堂小结
等腰三角形的判定和反正法
有两个角相等的三角形是等腰三角形
假设→归谬→结论
等角对等边
反证法
(第3课时)
北师大版 八年级 数学 下册
1、问题1:等腰三角形有哪些性质定理及推论?
等腰三角形的两底角相等(简写成 ‘‘等边对等角”).
等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合(简写成 ‘‘三线合一”)
问题2:等腰三角形的“等边对等角”的题设和结论分别是什么?
题设:一个三角形是等腰三角形
结论:相等的两边所对应的角相等
导入新知
它的逆命题成立吗?
导入新知
2、思考:如图,在△ABC中,如果∠B
=∠C,那么AB与AC之间有什么关系吗?
3cm
3cm
测量后发现AB与AC相等.
1. 掌握等腰三角形的判定定理及其运用.
2. 理解并掌握反证法的思想,能够运用反证法进行证明.
素养目标
等腰三角形性质定理:______________.
思考:我们把性质定理的条件和结论反过来还成立吗?
即:如果一个三角形有两个角相等,那么这个三角形是等腰三角形吗?
等边对等角
C
B
A
探究新知
知识点 1
等腰三角形的判定
位于海上B、C两处的两艘救生船接到A处遇险船只的报警,当时测得∠B=∠C.如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
探究新知
情景探究
已知:如图,在△ABC中, ∠B=∠C,那么它们所对的边AB和AC有什么数量关系?
建立数学模型:
C
A
B
AB=AC
做一做:画一个△ABC,其中∠B=∠C=30°.
请你量一量AB与AC的长度,它们之间有什么数量关系,你能得出什么结论?
AB=AC
你能验证你的结论吗?
探究新知
探究新知
已知:
求证:
AB=AC.
如图, 在△ABC中, ∠B=∠C.
猜想证明:
有两个角相等的三角形是等腰三角形.
在△ABD与△ACD中,
∠1=∠2,
∴ △ABD ≌ △ACD(AAS).
∠B=∠C,
AD=AD,
∴AB=AC.
过点A作AD平分∠BAC交BC于点D.
证明:
C
A
B
2
1
D
(
(
△ABC是等腰三角形.
有两个角相等的三角形是等腰三角形.
简述为:“等角对等边”
结论
探究新知
等腰三角形的判定定理:
在△ABC中,
∵∠B=∠C,
应用格式:
∴AB=AC(等角对等边).
A
C
B
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,
因为都不是在同一个三角形中.
辨一辨:如图,下列推理正确吗?
探究新知
等腰三角形的判定
素养考点 1
探究新知
例
已知:如图,AB=DC,BD=CA,BD与CA相交于点E.
求证:△AED是等腰三角形.
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS),
∴∠ADB=∠DAC(全等三角形的对应角相等),
∴AE=DE(等角对等边),
∴ △AED是等腰三角形.
巩固练习
变式训练
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4 cm,则CD等于 ( )
A.3 cm B.4 cm
C.1.5 cm D.2 cm
B
如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE相交于点O,给出四个条件:
①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.
上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有( )
A.2种 B.3种 C.4种 D.6种
C
巩固练习
变式训练
探究新知
知识点 2
反证法
想一想:小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
即在△ABC中, 如果∠B≠∠C,那么AB≠AC.
A
B
C
探究新知
C
A
B
如图,在△ABC中,已知∠B≠∠C,
此时, AB与AC要么相等,要么不相等.
假设AB=AC, 那么根据“等边对等角”定理可得∠B=∠C,
但已知条件是 ∠B≠∠C,“∠B=∠C”与“∠B≠∠C”相矛盾,因此AB≠AC.
小明是这样想的:
你能理解他的推理过程吗?
利用了“反证法”
探究新知
结论
在证明时,先假设命题的结论不成立,然后由此推导出与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
探究新知
①假设: 先假设命题的结论不成立;
②归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
③结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
用反证法证题的一般步骤:
用反证法证明:一个三角形中不能有两个角是直角.
证明:假设∠A、∠B、∠C中有两个角是直角,
不妨设∠A和∠B是直角,即∠A=90°,∠B=90°.
则∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,
所以“∠A和∠B是直角”的假设不成立.
所以一个三角形中不能有两个角是直角.
反证法
素养考点 2
例
探究新知
已知:△ABC.
求证:∠A、∠B、∠C中不能有两个角是直角.
巩固练习
变式训练
用反证法证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
已知:如图,直线l1,l2被l3所截,∠1+∠2=180°.
求证:l1∥l2.
证明:假设l1不平行于l2,即l1与l2相交于一点P.
则∠1+∠2+∠P=180°, 所以∠1+∠2<180°,
这与已知矛盾,故假设不成立.
所以l1∥l2.
巩固练习
变式训练
1.用反证法证明“a>b”时,应假设 ( )
A. a2.用反证法证明命题“四边形的四个内角中至少有一个角大于等于90°”,我们应该假设 ( )
A.四个角都小于90°
B.最多有一个角大于或等于90°
C.有两个角小于90°
D.四个角都大于或等于90°
B
A
连接中考
(2020·南充)如图,在等腰△ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= ( )
A. B.
C. a-b D. b-a
C
E
2
1
A
B
C
D
72°
36°
③如果AD=4cm,则
1.已知:如图,∠A=36°,
∠DBC=36°,∠C=72°,
①∠1= , ∠2= ;
②图中有 个等腰三角形;
BC= cm;
72°
36°
3
4
个等腰三角形.
④如果过点D作DE∥BC,
交AB于点E,则图中有
5
课堂检测
基础巩固题
2.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,
下列条件中,不能判定△ABC是等腰三角形的是( )
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
D
课堂检测
基础巩固题
3、如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=
∠DBC=36°,则图中等腰三角形的个数是 ( )
A.2 B.3
C.4 D.5
D
课堂检测
基础巩固题
4、如图,在平面直角坐标系中,点B,A分别在x轴,y轴上,
∠BAO=60°,在坐标轴上找一点P,使得△ABP是等腰三
角形,则符合条件的等腰三角形ABP有______个.?
6
课堂检测
基础巩固题
5、如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E.求证:BD+EC=DE.
证明:∵BF平分∠ABC,∴∠1=∠2,
又DE∥BC,∴∠2=∠3,
∴∠1=∠3,
∴DB=DF(等角对等边),
同理可得:EC=EF,
∵DF+EF=DE,
∴BD+EC=DE.
课堂检测
基础巩固题
1、已知如图,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F.求证:AD垂直平分EF.
证明:∵AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∴∠1=∠2,
易得∠AED=∠AFD=90°,∴∠3=∠4,
∴AE=AF,
∵AD是等腰△AEF的顶角平分线,
∴AD垂直平分EF.
课堂检测
能力提升题
2、如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.
求证:△BDE是等腰三角形.
证明:∵DE∥AC,∴∠CAD=∠EDA,
∵AD平分∠BAC,∴∠CAD=∠EAD,
∴∠EAD=∠EDA,
∵AD⊥BD,∴∠EAD+∠B=90°,∠EDA+∠BDE=90°,
∴∠B=∠BDE,∴△BDE是等腰三角形.
课堂检测
能力提升题
如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.
求证:△AEF是等腰三角形.
证明:∵FD∥AC,∴∠PFD=∠E,∠FDB= ∠C,
∵AB=AC,∴ ∠B = ∠C,∴∠FDB=∠B,∴FB=FD,
∵FB=FD,EP⊥BC,∴∠PFB=∠PFD,
∵∠PFB=∠AFE,∴∠PFD=∠AFE,
∵∠PFD=∠E,∴∠E=∠AFE, ∴AE=AF, ?
即△AEF是等腰三角形.
课堂检测
拓广探索题
课堂小结
等腰三角形的判定和反正法
有两个角相等的三角形是等腰三角形
假设→归谬→结论
等角对等边
反证法
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
