北师大版八年级数学下册1.1 等腰三角形课件(第1课时 33张)
文档属性
| 名称 | 北师大版八年级数学下册1.1 等腰三角形课件(第1课时 33张) |  | |
| 格式 | pptx | ||
| 文件大小 | 769.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:01:28 | ||
图片预览









文档简介
1.1 等腰三角形
(第1课时)
北师大版 八年级 数学 下册
1、图中有你熟悉的图形吗?它们有什么共同特点?
斜拉桥梁
埃及金字塔
体育观看台架
导入新知
2、在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
①两点确定一条直线;
②两点之间线段最短;
③同一平面内,过一点有且只有一条直线与已知直线垂直;
④同位角相等,两直线平行;
⑤过直线外一点有且只有一条直线与这条直线平行;
⑥两边及其夹角分别相等的两个三角形全等;
⑦两角及其夹边分别相等的两个三角形全等;
⑧三边分别相等的两个三角形全等.
导入新知
1. 回顾全等三角形的判定和性质.
2. 理解并掌握等腰三角形的性质及其推论.
素养目标
3. 能运用等腰三角形的性质及其推论解决基本的几何问题.
探究新知
知识点 1
全等三角形的判定和性质
两角分别相等且其中一组等角的对边相等的两个三角形全等.
在“平行线的证明”这一章中,我们学了8条基本事实定理.运用这些基本事实和已学习的定理,你能证明有关三角形全等的一些结论吗?
比如:
探究新知
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
思考:证明命题的步骤是什么?
探究新知
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知), ∴∠C=∠F(等量代换).
∵BC=EF(已知),∴△ABC≌△DEF(ASA).
探究新知
结论
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.
根据全等三角形的定义,我们可以得到:
全等三角形的对应边相等,对应角相等.
结论
全等三角形的判定与性质
素养考点 1
探究新知
例 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
D
方法总结
判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS.
注意:AAA,SSA不能判定两个三角形全等,判定两个三角
形全等时,必须有边的参与,若有两边一角对应相等时,角
必须是两边的夹角.
探究新知
巩固练习
变式训练
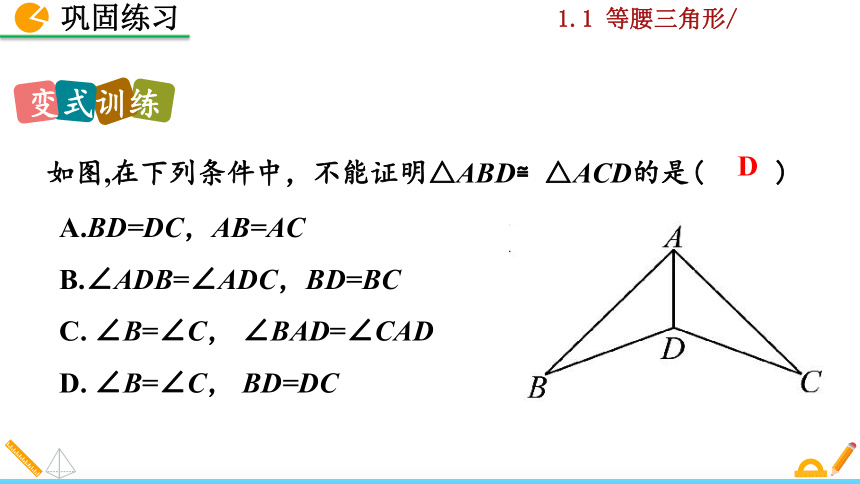
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=BC
C. ∠B=∠C, ∠BAD=∠CAD
D. ∠B=∠C, BD=DC
D
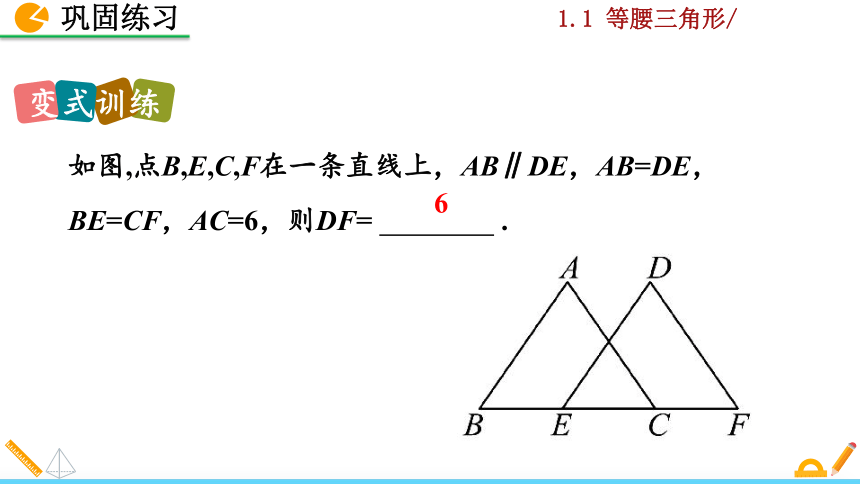
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= .
6
巩固练习
变式训练
探究新知
知识点 2
等腰三角形的性质定理及其推论
你还记得我们探索过的等腰三角形的性质吗?
推论:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合.
思考2:你能利用已有的公理和定理证明这些结论吗?
定理:等腰三角形的两个底角相等.
思考1:
探究新知
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明定理:等腰三角形的两个底角相等.
A
B
C
思考:如何证明两个角相等呢?
在七下学习轴对称时,我们利用折叠的方法说明了等腰三角形是轴对称图形,且两个底角相等,如下图,实际上,折痕将等腰三角形分成了两个全等的三角形.由此,你得到了什么解题的启发?
探究新知
可以作一条辅助线,运用全等三角形的性质“对应角相等”来证.
思考:如何构造两个全等的三角形?
探究新知
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法一:作底边上的中线
探究新知
A
B
C
D
证明:
作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法二:作顶角的平分线
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
探究新知
结论
定理 等腰三角形的两个底角相等.
这一定理可简述为:“等边对等角”.
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?
探究新知
∵△BAD≌ △CAD,
∴由全等三角形的性质易得
BD=CD,
∠BAD=∠CAD,
∠ADB=∠ADC,
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90°.
A
B
C
D
AD是底边BC上的中线
AD是顶角∠BAC的
角平分线
AD是底边BC上
的高线
3、线段AD的性质
探究新知
结论
推论 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
(1)∵AB=AC,AD⊥BC
∴ (三线合一)
(2)∵AB=AC,BD=CD
∴_________________________(三线合一)
(3)∵AB=AC, ∠BAD=∠CAD
∴____________________ (三线合一)
BD=CD,∠BAD=∠CAD
AD⊥BC,∠BAD=∠CAD
AD⊥BC ,BD=CD
D
C
B
A
等腰三角形的性质定理
素养考点 1
探究新知
例1 (1)若等腰三角形的一个底角为72°,则这个等腰三角形的顶角为_________.?
(2)在△ABC中,AB=AC,∠A=40°,则∠B=_______°.
36°
70
如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A.50° B.60°
C.70° D.80°
B
巩固练习
变式训练
等腰三角形性质定理的推论
素养考点 2
探究新知
例2 如图,△ABC中,AB=AC,垂足为点D,若∠BAC=70°,则∠BAD= .
35°
巩固练习
变式训练
如图, 在△ABC中,AC=BC,用尺规作CF⊥AB,交AB于 点G,若∠BCG=50°,则∠A的度数为 ( )
A.40° B.45°
C.50° D.60°
A
连接中考
(2020·呼伦贝尔)如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 ( )
A.25° B.20°
C.30° D.15°
D
1.一个等腰三角形的顶角是50°,则它的底角是( )
A
A.65° B.70° C.75° D.100°
课堂检测
基础巩固题
2.如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
D
A.40° B.50° C.60° D.70°
3.如图,已知AD=BC,∠1=∠2,则下列说法正确的是 ( )
A.BD=AC B.∠D=∠C
C.∠DAB=∠CBA D.以上说法都不对
D
课堂检测
基础巩固题
4.如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是 .
AC=DF
课堂检测
基础巩固题
基础巩固题
5.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B=( )
A
A.70° B.30° C.40° D.20°
课堂检测
1.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与
BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度
数为( )
A.30° B.15° C.25° D.20°
D
课堂检测
能力提升题
能力提升题
2.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
A
课堂检测
拓广探索题
如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
解:∵AB=AC,∴∠ABC=∠C,
∵∠C=2∠A, 设∠A=x,则∠ABC=∠C=2x,
由x+2x+2x=180°得x=36°,
∴∠A=36°,∠C=72°,
∵BD是AC边上的高,∴BD⊥AC,即∠BDC=90°,
∴∠DBC=90°-∠C=18°.
课堂检测
等腰三角形
性质
等边对等角
课堂小结
推论
三线合一
全等三角形
判定
SSS,SAS,ASA,AAS
性质
对应边相等,对应角相等
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
(第1课时)
北师大版 八年级 数学 下册
1、图中有你熟悉的图形吗?它们有什么共同特点?
斜拉桥梁
埃及金字塔
体育观看台架
导入新知
2、在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
①两点确定一条直线;
②两点之间线段最短;
③同一平面内,过一点有且只有一条直线与已知直线垂直;
④同位角相等,两直线平行;
⑤过直线外一点有且只有一条直线与这条直线平行;
⑥两边及其夹角分别相等的两个三角形全等;
⑦两角及其夹边分别相等的两个三角形全等;
⑧三边分别相等的两个三角形全等.
导入新知
1. 回顾全等三角形的判定和性质.
2. 理解并掌握等腰三角形的性质及其推论.
素养目标
3. 能运用等腰三角形的性质及其推论解决基本的几何问题.
探究新知
知识点 1
全等三角形的判定和性质
两角分别相等且其中一组等角的对边相等的两个三角形全等.
在“平行线的证明”这一章中,我们学了8条基本事实定理.运用这些基本事实和已学习的定理,你能证明有关三角形全等的一些结论吗?
比如:
探究新知
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
思考:证明命题的步骤是什么?
探究新知
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.(AAS)
∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知), ∴∠C=∠F(等量代换).
∵BC=EF(已知),∴△ABC≌△DEF(ASA).
探究新知
结论
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.
根据全等三角形的定义,我们可以得到:
全等三角形的对应边相等,对应角相等.
结论
全等三角形的判定与性质
素养考点 1
探究新知
例 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE
C.BD=CE D.BE=CD
D
方法总结
判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS.
注意:AAA,SSA不能判定两个三角形全等,判定两个三角
形全等时,必须有边的参与,若有两边一角对应相等时,角
必须是两边的夹角.
探究新知
巩固练习
变式训练
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
A.BD=DC,AB=AC
B.∠ADB=∠ADC,BD=BC
C. ∠B=∠C, ∠BAD=∠CAD
D. ∠B=∠C, BD=DC
D
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF= .
6
巩固练习
变式训练
探究新知
知识点 2
等腰三角形的性质定理及其推论
你还记得我们探索过的等腰三角形的性质吗?
推论:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合.
思考2:你能利用已有的公理和定理证明这些结论吗?
定理:等腰三角形的两个底角相等.
思考1:
探究新知
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明定理:等腰三角形的两个底角相等.
A
B
C
思考:如何证明两个角相等呢?
在七下学习轴对称时,我们利用折叠的方法说明了等腰三角形是轴对称图形,且两个底角相等,如下图,实际上,折痕将等腰三角形分成了两个全等的三角形.由此,你得到了什么解题的启发?
探究新知
可以作一条辅助线,运用全等三角形的性质“对应角相等”来证.
思考:如何构造两个全等的三角形?
探究新知
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法一:作底边上的中线
探究新知
A
B
C
D
证明:
作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法二:作顶角的平分线
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
探究新知
结论
定理 等腰三角形的两个底角相等.
这一定理可简述为:“等边对等角”.
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?
探究新知
∵△BAD≌ △CAD,
∴由全等三角形的性质易得
BD=CD,
∠BAD=∠CAD,
∠ADB=∠ADC,
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90°.
A
B
C
D
AD是底边BC上的中线
AD是顶角∠BAC的
角平分线
AD是底边BC上
的高线
3、线段AD的性质
探究新知
结论
推论 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
(1)∵AB=AC,AD⊥BC
∴ (三线合一)
(2)∵AB=AC,BD=CD
∴_________________________(三线合一)
(3)∵AB=AC, ∠BAD=∠CAD
∴____________________ (三线合一)
BD=CD,∠BAD=∠CAD
AD⊥BC,∠BAD=∠CAD
AD⊥BC ,BD=CD
D
C
B
A
等腰三角形的性质定理
素养考点 1
探究新知
例1 (1)若等腰三角形的一个底角为72°,则这个等腰三角形的顶角为_________.?
(2)在△ABC中,AB=AC,∠A=40°,则∠B=_______°.
36°
70
如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A.50° B.60°
C.70° D.80°
B
巩固练习
变式训练
等腰三角形性质定理的推论
素养考点 2
探究新知
例2 如图,△ABC中,AB=AC,垂足为点D,若∠BAC=70°,则∠BAD= .
35°
巩固练习
变式训练
如图, 在△ABC中,AC=BC,用尺规作CF⊥AB,交AB于 点G,若∠BCG=50°,则∠A的度数为 ( )
A.40° B.45°
C.50° D.60°
A
连接中考
(2020·呼伦贝尔)如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 ( )
A.25° B.20°
C.30° D.15°
D
1.一个等腰三角形的顶角是50°,则它的底角是( )
A
A.65° B.70° C.75° D.100°
课堂检测
基础巩固题
2.如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
D
A.40° B.50° C.60° D.70°
3.如图,已知AD=BC,∠1=∠2,则下列说法正确的是 ( )
A.BD=AC B.∠D=∠C
C.∠DAB=∠CBA D.以上说法都不对
D
课堂检测
基础巩固题
4.如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是 .
AC=DF
课堂检测
基础巩固题
基础巩固题
5.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B=( )
A
A.70° B.30° C.40° D.20°
课堂检测
1.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与
BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度
数为( )
A.30° B.15° C.25° D.20°
D
课堂检测
能力提升题
能力提升题
2.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
A
课堂检测
拓广探索题
如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
解:∵AB=AC,∴∠ABC=∠C,
∵∠C=2∠A, 设∠A=x,则∠ABC=∠C=2x,
由x+2x+2x=180°得x=36°,
∴∠A=36°,∠C=72°,
∵BD是AC边上的高,∴BD⊥AC,即∠BDC=90°,
∴∠DBC=90°-∠C=18°.
课堂检测
等腰三角形
性质
等边对等角
课堂小结
推论
三线合一
全等三角形
判定
SSS,SAS,ASA,AAS
性质
对应边相等,对应角相等
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
