北师大版八年级数学下册1.2 直角三角形(第1课时)课件(39张)
文档属性
| 名称 | 北师大版八年级数学下册1.2 直角三角形(第1课时)课件(39张) |  | |
| 格式 | pptx | ||
| 文件大小 | 592.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:02:16 | ||
图片预览









文档简介
1.2 直角三角形
(第1课时)
北师大版 八年级 数学 下册
导入新知
(2)直角三角形的定义是什么?
(3)三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
思考:(1)三角形的分类?
锐角三角形,直角三角形,钝角三角形.
直角三角形的两个锐角互余.
这节课我们一起来证明直角三角形的判定与性质.
(4) 前面我们探究过直角三角形的哪些性质?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
导入新知
1.复习直角三角形的相关知识,归纳并掌握直角三角形的性质和判定.
2.学习并掌握勾股定理及其逆定理,能够运用其解决问题.
素养目标
3.结合具体事例理解互逆命题、互逆定理的概念,并体会原命题成立时,其逆命题不一定成立.
探究新知
知识点 1
直角三角形的性质与判定
思考:
(1)直角三角形的两个锐角有怎样的关系?
根据三角形的内角和定理,即可得到“直角三角形的两锐角互余”.
(2)如果一个三角形中有两个角互余,那么这个三角形是直角三角形吗?
是直角三角形.
已知:如图,在△ABC中, ∠A +∠B=90°.
求证: △ABC是直角三角形.
在△ABC中,
∵ ∠A +∠B +∠C=180°,
又∠A +∠B=90°,∴∠C=90°,
∴△ABC是直角三角形.
证明:
如果一个三角形中有两个角互余,那么这个三角形是直角三角形.
证明:
探究新知
性质定理 直角三角形的两锐角互余.
直角三角形的性质与判定
结论
判定定理 有两个角互余的三角形是直角三角形.
探究新知
直角三角形的性质与判定
素养考点 1
探究新知
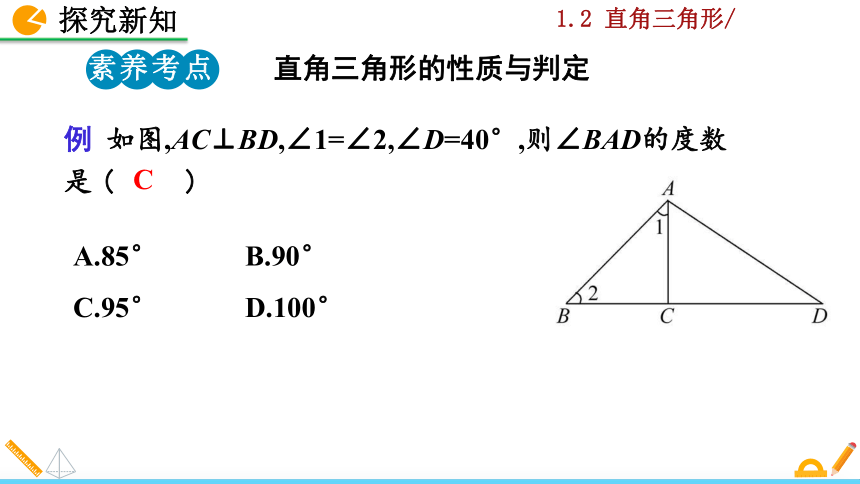
例 如图,AC⊥BD,∠1=∠2,∠D=40°,则∠BAD的度数是 ( )
A.85° B.90°
C.95° D.100°
C
巩固练习
变式训练
直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_________.
30°
知识点 2
勾股定理与逆定理
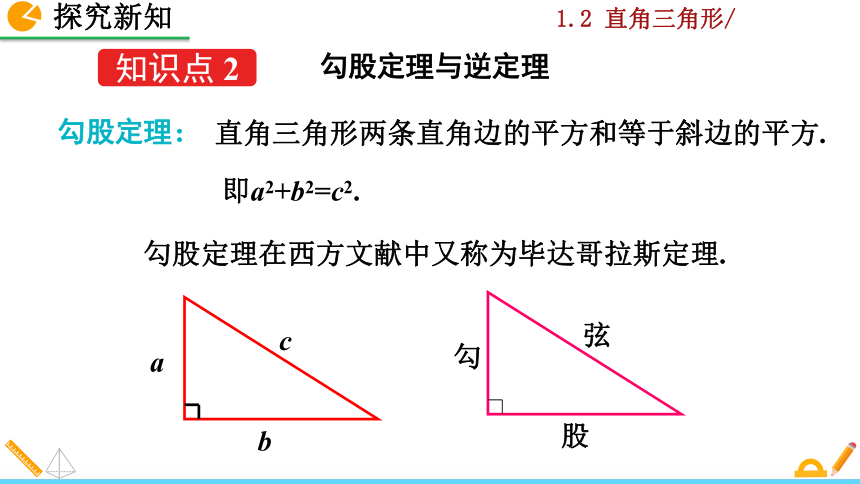
勾股定理:
直角三角形两条直角边的平方和等于斜边的平方.
即a2+b2=c2.
a
c
b
勾
弦
股
勾股定理在西方文献中又称为毕达哥拉斯定理.
探究新知
勾股定理的3种证明方法:
b
a
c
b
a
c
方法一:
探究新知
探究新知
方法二:
c
a
b
c
a
b
c
a
b
c
a
b
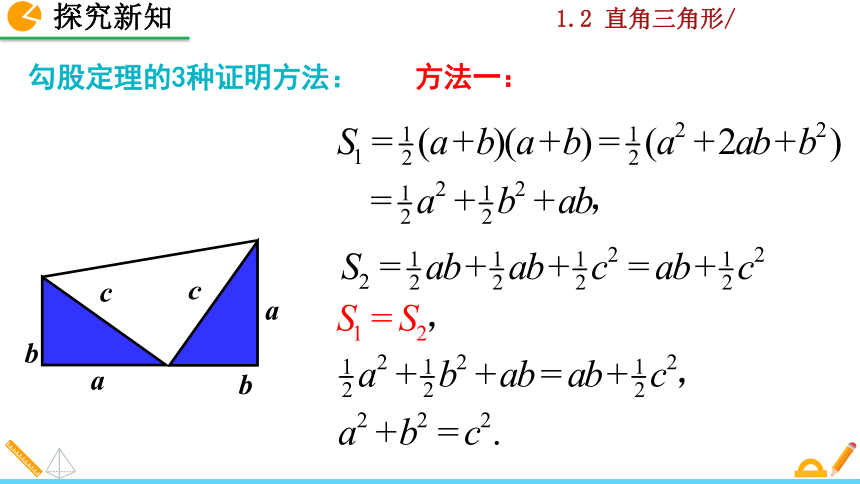
∵ (a+b)2 = c2+ ,
a2+2ab+b2 = c2+2ab,
∴a2+b2=c2.
大正方形的面积可以表示为 ;
也可以表示为 ;
(a+b)2
c2+
探究新知
探究新知
方法三:
c
∵ c2= +(b-a)2,
c2 =2ab+b2-2ab+a2,
c2 =a2+b2,
∴ a2+b2=c2.
大正方形的面积可以表示为 ;
也可以表示为 .
c2
+(b-a)2
c
a
c
a
c
b
a
a
b
b
b
探究新知
勾股定理的逆定理:
我们曾用度量的办法得出这个结论.
勾股定理反过来,怎么叙述呢?
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
思考:这个命题是真命题吗?为什么?
是否还有其他方法?
探究新知
勾股定理的逆定理的证明:
已知:如图,在△ABC中,AC2+BC2=AB2.
求证:△ABC是直角三角形.
分析:构造一个直角三角形与△ABC全等,你能自己写出证明过程吗?
A
B
C
证明:作Rt△DEF,使∠E=90°,
DE=AC,FE=BC,则DE2+EF2=DF2(勾股定理).
∵AC2+BC2=AB2(已知), DE=AC,FE=BC(作图),
∴AB2=DF2,∴AB=DF,
∴△ABC≌△DFE(SSS).
∴∠C=∠E=90°,
∴△ABC是直角三角形.
D
F
E
┏
A
B
C
探究新知
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理与逆定理
结论
逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
探究新知
小结
直角三角形的性质定理:
1.直角三角形的两个锐角互余.
2.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
直角三角形的判定定理:
1.有两个角互余的三角形是直角三角形
2.如果三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形.
直角三角形的性质与判定
探究新知
勾股定理与逆定理
素养考点 2
探究新知
例 已知△ABC的三边长分别为5、12、13,则△ABC的面积为 ( )
A.30 B.60
C.78 D.不能确定
A
巩固练习
变式训练
已知:如图,在△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长.
解:∵△ABC是直角三角形,AB=5cm,BC=3cm,
由勾股定理得AC2=AB2-BC2,∴AC=4cm,
又S△ABC= BC·AC= AB·CD,
CD=BC·AC÷AB=2.4cm,
∴CD的长是2.4cm.
探究新知
知识点 3
互逆命题与互逆定理
观察:
定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
下面两个定理的条件和结论有什么样的关系?
一个命题的条件和结论分别是另一个命题的结论和条件.
上面每组中两个命题的条件和结论也有类似的关系吗?
与同伴交流.
观察下面三组命题:
探究新知
探究新知
上面每两个命题的条件和结论恰好互换了位置.
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
注意:原命题是真命题,而逆命题不一定是真命题!
互逆命题:
探究新知
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,我们称它们为互逆定理.其中一个定理称为另一个定理的逆定理.
互逆定理:
注意:(1)逆命题、互逆命题不一定是真命题,但逆定理、互逆定理,一定是真命题.
(2)每个定理都有逆命题,但每个定理不一定有逆定理.
互逆命题与互逆定理
素养考点 3
探究新知
例 指出下列命题的条件和结论,并说出它们的逆命题.
条件:一个三角形是直角三角形.
结论:它的两个锐角互余.
逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形.
(1)如果一个三角形是直角三角形,那么它的两个锐角互余.
探究新知
条件:一个三角形是等边三角形.
结论:它的每个角都等于60°.
逆命题:如果一个三角形的每个角都等于60°,那么这个三角形是等边三角形.
(2)等边三角形的每个角都等于60°.
探究新知
条件:两个三角形是全等三角形.
结论:它们的对应角相等.
逆命题:如果两个三角形的对应角相等,那么这两个三角形全等.
(3)全等三角形的对应角相等.
巩固练习
变式训练
下列命题:
①直角三角形两条直角边的平方和等于斜边的平方;
②若a>b,则ac2>bc2;
③全等三角形对应角相等;
④直角三角形两锐角互余.
其中原命题与逆命题均为真命题的是( )
A.①②④ B.①④
C.③④ D.④
B
连接中考
(2020·荆门)△ABC中,AB=AC,∠BAC=120°,BC= ,D为BC的中点,AE= AB,则△EBD的面积为( )
B
A. B.
C. D.
1. 在一个直角三角形中,有一个锐角等于35°,则另一
个锐角的度数是( )
A.75° B.65° C.55° D.45°
C
课堂检测
基础巩固题
2. 如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
B
课堂检测
基础巩固题
3. 下列长度的三条线段能组成直角三角形的是 ( )
A.3,4,5 B.2,3,4
C.4,6,7 D.5,11,12
A
4.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形的形状是_________三角形.
直角
课堂检测
基础巩固题
5.“直角都相等”与“相等的角是直角”是 ( )
A.互为逆命题 B.互逆定理
C.公理 D.假命题
A
课堂检测
基础巩固题
1、如图,△ABC中,AB=AC,∠BAC=90°,D是BC上任一点.求证:BD2+CD2=2AD2.
证明:
过点A作AE⊥BC于E,
则在Rt△ADE中,AD2=DE2+AE2,
又∵AB=AC,∠BAC=90°,
∴AE=BE=CE,
∵BD2+CD2=(BE-DE)2+(CE+DE)2
=BE2+CE2+2DE2=2AE2+2DE2=2AD2,
即BD2+CD2=2AD2.
课堂检测
能力提升题
E
2、如图,直角三角形ABC中,∠ACB=90°,AC=12cm,BC=5cm,
AB=13 cm,过点C作CD⊥AB于点D.
解:(1)∵CD⊥AB(已知),
∴∠CDA=90°,∴∠A+∠1=90°,
∵∠1+∠2=90°,∴∠A=∠2.
同理可得,∠1=∠B.
(1)找出图中相等的锐角,并说明理由.
课堂检测
能力提升题
解:(2)点A到直线BC的距离为12 cm.
点C到直线AB的距离为线段CD的长度.
S△ABC= AC×BC= AB×CD.
∵AC=12 cm,BC=5 cm,AB=13 cm,
代入上式,解得CD= cm.
(2)求出点A到直线BC的距离以及点C到直线AB的距离.
课堂检测
如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
求四边形ABCD的面积.
解:连接AC,
∵∠B=90°,AB=BC=2,∴AC=2 ,
∵AD=1,CD=3,
∴AD2+AC2=12+(2 )2=9,CD2=9,
课堂检测
拓广探索题
∴AD2+AC2=CD2,
∴△ADC是直角三角形,∴∠DAC=90°,
在Rt△ABC中,S△ABC= BC·AB= ×2×2=2,
在Rt△ADC中,S△ADC= AD·AC= ×1×2 = ,
∴S四边形ABCD=S△ABC+S△ADC=2+ .
课堂检测
课堂小结
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形.
直角三角形
互逆命题与互逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
角的性质
边的性质
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件.
一个定理的逆命题也是定理,这两个定理叫做互逆定理
互逆命题
互逆定理
(第1课时)
北师大版 八年级 数学 下册
导入新知
(2)直角三角形的定义是什么?
(3)三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
思考:(1)三角形的分类?
锐角三角形,直角三角形,钝角三角形.
直角三角形的两个锐角互余.
这节课我们一起来证明直角三角形的判定与性质.
(4) 前面我们探究过直角三角形的哪些性质?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
导入新知
1.复习直角三角形的相关知识,归纳并掌握直角三角形的性质和判定.
2.学习并掌握勾股定理及其逆定理,能够运用其解决问题.
素养目标
3.结合具体事例理解互逆命题、互逆定理的概念,并体会原命题成立时,其逆命题不一定成立.
探究新知
知识点 1
直角三角形的性质与判定
思考:
(1)直角三角形的两个锐角有怎样的关系?
根据三角形的内角和定理,即可得到“直角三角形的两锐角互余”.
(2)如果一个三角形中有两个角互余,那么这个三角形是直角三角形吗?
是直角三角形.
已知:如图,在△ABC中, ∠A +∠B=90°.
求证: △ABC是直角三角形.
在△ABC中,
∵ ∠A +∠B +∠C=180°,
又∠A +∠B=90°,∴∠C=90°,
∴△ABC是直角三角形.
证明:
如果一个三角形中有两个角互余,那么这个三角形是直角三角形.
证明:
探究新知
性质定理 直角三角形的两锐角互余.
直角三角形的性质与判定
结论
判定定理 有两个角互余的三角形是直角三角形.
探究新知
直角三角形的性质与判定
素养考点 1
探究新知
例 如图,AC⊥BD,∠1=∠2,∠D=40°,则∠BAD的度数是 ( )
A.85° B.90°
C.95° D.100°
C
巩固练习
变式训练
直角三角形中,一个锐角等于另一个锐角的2倍,则较小的锐角是_________.
30°
知识点 2
勾股定理与逆定理
勾股定理:
直角三角形两条直角边的平方和等于斜边的平方.
即a2+b2=c2.
a
c
b
勾
弦
股
勾股定理在西方文献中又称为毕达哥拉斯定理.
探究新知
勾股定理的3种证明方法:
b
a
c
b
a
c
方法一:
探究新知
探究新知
方法二:
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2+ ,
a2+2ab+b2 = c2+2ab,
∴a2+b2=c2.
大正方形的面积可以表示为 ;
也可以表示为 ;
(a+b)2
c2+
探究新知
探究新知
方法三:
c
∵ c2= +(b-a)2,
c2 =2ab+b2-2ab+a2,
c2 =a2+b2,
∴ a2+b2=c2.
大正方形的面积可以表示为 ;
也可以表示为 .
c2
+(b-a)2
c
a
c
a
c
b
a
a
b
b
b
探究新知
勾股定理的逆定理:
我们曾用度量的办法得出这个结论.
勾股定理反过来,怎么叙述呢?
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
思考:这个命题是真命题吗?为什么?
是否还有其他方法?
探究新知
勾股定理的逆定理的证明:
已知:如图,在△ABC中,AC2+BC2=AB2.
求证:△ABC是直角三角形.
分析:构造一个直角三角形与△ABC全等,你能自己写出证明过程吗?
A
B
C
证明:作Rt△DEF,使∠E=90°,
DE=AC,FE=BC,则DE2+EF2=DF2(勾股定理).
∵AC2+BC2=AB2(已知), DE=AC,FE=BC(作图),
∴AB2=DF2,∴AB=DF,
∴△ABC≌△DFE(SSS).
∴∠C=∠E=90°,
∴△ABC是直角三角形.
D
F
E
┏
A
B
C
探究新知
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
勾股定理与逆定理
结论
逆定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
探究新知
小结
直角三角形的性质定理:
1.直角三角形的两个锐角互余.
2.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
直角三角形的判定定理:
1.有两个角互余的三角形是直角三角形
2.如果三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形.
直角三角形的性质与判定
探究新知
勾股定理与逆定理
素养考点 2
探究新知
例 已知△ABC的三边长分别为5、12、13,则△ABC的面积为 ( )
A.30 B.60
C.78 D.不能确定
A
巩固练习
变式训练
已知:如图,在△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长.
解:∵△ABC是直角三角形,AB=5cm,BC=3cm,
由勾股定理得AC2=AB2-BC2,∴AC=4cm,
又S△ABC= BC·AC= AB·CD,
CD=BC·AC÷AB=2.4cm,
∴CD的长是2.4cm.
探究新知
知识点 3
互逆命题与互逆定理
观察:
定理:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
下面两个定理的条件和结论有什么样的关系?
一个命题的条件和结论分别是另一个命题的结论和条件.
上面每组中两个命题的条件和结论也有类似的关系吗?
与同伴交流.
观察下面三组命题:
探究新知
探究新知
上面每两个命题的条件和结论恰好互换了位置.
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
注意:原命题是真命题,而逆命题不一定是真命题!
互逆命题:
探究新知
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,我们称它们为互逆定理.其中一个定理称为另一个定理的逆定理.
互逆定理:
注意:(1)逆命题、互逆命题不一定是真命题,但逆定理、互逆定理,一定是真命题.
(2)每个定理都有逆命题,但每个定理不一定有逆定理.
互逆命题与互逆定理
素养考点 3
探究新知
例 指出下列命题的条件和结论,并说出它们的逆命题.
条件:一个三角形是直角三角形.
结论:它的两个锐角互余.
逆命题:如果一个三角形的两个锐角互余,那么这个三角形是直角三角形.
(1)如果一个三角形是直角三角形,那么它的两个锐角互余.
探究新知
条件:一个三角形是等边三角形.
结论:它的每个角都等于60°.
逆命题:如果一个三角形的每个角都等于60°,那么这个三角形是等边三角形.
(2)等边三角形的每个角都等于60°.
探究新知
条件:两个三角形是全等三角形.
结论:它们的对应角相等.
逆命题:如果两个三角形的对应角相等,那么这两个三角形全等.
(3)全等三角形的对应角相等.
巩固练习
变式训练
下列命题:
①直角三角形两条直角边的平方和等于斜边的平方;
②若a>b,则ac2>bc2;
③全等三角形对应角相等;
④直角三角形两锐角互余.
其中原命题与逆命题均为真命题的是( )
A.①②④ B.①④
C.③④ D.④
B
连接中考
(2020·荆门)△ABC中,AB=AC,∠BAC=120°,BC= ,D为BC的中点,AE= AB,则△EBD的面积为( )
B
A. B.
C. D.
1. 在一个直角三角形中,有一个锐角等于35°,则另一
个锐角的度数是( )
A.75° B.65° C.55° D.45°
C
课堂检测
基础巩固题
2. 如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
B
课堂检测
基础巩固题
3. 下列长度的三条线段能组成直角三角形的是 ( )
A.3,4,5 B.2,3,4
C.4,6,7 D.5,11,12
A
4.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形的形状是_________三角形.
直角
课堂检测
基础巩固题
5.“直角都相等”与“相等的角是直角”是 ( )
A.互为逆命题 B.互逆定理
C.公理 D.假命题
A
课堂检测
基础巩固题
1、如图,△ABC中,AB=AC,∠BAC=90°,D是BC上任一点.求证:BD2+CD2=2AD2.
证明:
过点A作AE⊥BC于E,
则在Rt△ADE中,AD2=DE2+AE2,
又∵AB=AC,∠BAC=90°,
∴AE=BE=CE,
∵BD2+CD2=(BE-DE)2+(CE+DE)2
=BE2+CE2+2DE2=2AE2+2DE2=2AD2,
即BD2+CD2=2AD2.
课堂检测
能力提升题
E
2、如图,直角三角形ABC中,∠ACB=90°,AC=12cm,BC=5cm,
AB=13 cm,过点C作CD⊥AB于点D.
解:(1)∵CD⊥AB(已知),
∴∠CDA=90°,∴∠A+∠1=90°,
∵∠1+∠2=90°,∴∠A=∠2.
同理可得,∠1=∠B.
(1)找出图中相等的锐角,并说明理由.
课堂检测
能力提升题
解:(2)点A到直线BC的距离为12 cm.
点C到直线AB的距离为线段CD的长度.
S△ABC= AC×BC= AB×CD.
∵AC=12 cm,BC=5 cm,AB=13 cm,
代入上式,解得CD= cm.
(2)求出点A到直线BC的距离以及点C到直线AB的距离.
课堂检测
如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
求四边形ABCD的面积.
解:连接AC,
∵∠B=90°,AB=BC=2,∴AC=2 ,
∵AD=1,CD=3,
∴AD2+AC2=12+(2 )2=9,CD2=9,
课堂检测
拓广探索题
∴AD2+AC2=CD2,
∴△ADC是直角三角形,∴∠DAC=90°,
在Rt△ABC中,S△ABC= BC·AB= ×2×2=2,
在Rt△ADC中,S△ADC= AD·AC= ×1×2 = ,
∴S四边形ABCD=S△ABC+S△ADC=2+ .
课堂检测
课堂小结
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形.
直角三角形
互逆命题与互逆定理
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
角的性质
边的性质
第一个命题的条件是第二个命题的结论;
第一个命题的结论是第二个命题的条件.
一个定理的逆命题也是定理,这两个定理叫做互逆定理
互逆命题
互逆定理
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
