北师大版八年级数学下册1.1 等腰三角形课件(第4课时 33张)
文档属性
| 名称 | 北师大版八年级数学下册1.1 等腰三角形课件(第4课时 33张) |  | |
| 格式 | pptx | ||
| 文件大小 | 802.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:00:42 | ||
图片预览









文档简介
1.1 等腰三角形
(第4课时)
北师大版 八年级 数学 下册
导入新知
观察下面图片,说说它们都是由什么图形组成的?
思考:上节课我们学习了等腰三角形的判定定理,那等边三角形的判定定理是什么呢?
1. 能用所学的知识证明等边三角形的判定定理.
2. 掌握含30°角的直角三角形的性质并解决有关问题.
素养目标
探究新知
知识点 1
等边三角形的判定
(2) 一个三角形满足什么条件时是等边三角形?
(3)一个等腰三角形满足什么条件时是等边三角形?
有一个角是60°的等腰三角形是等边三角形.
三条边相等的三角形是等边三角形(定 义).
三个角相等的三角形是等边三角形.
(1)等边三角形有哪些性质?
等边三角形的三条边相等,三个角相等,“三线合一”.
思考:
你能证明这些定理吗?
探究新知
A
B
C
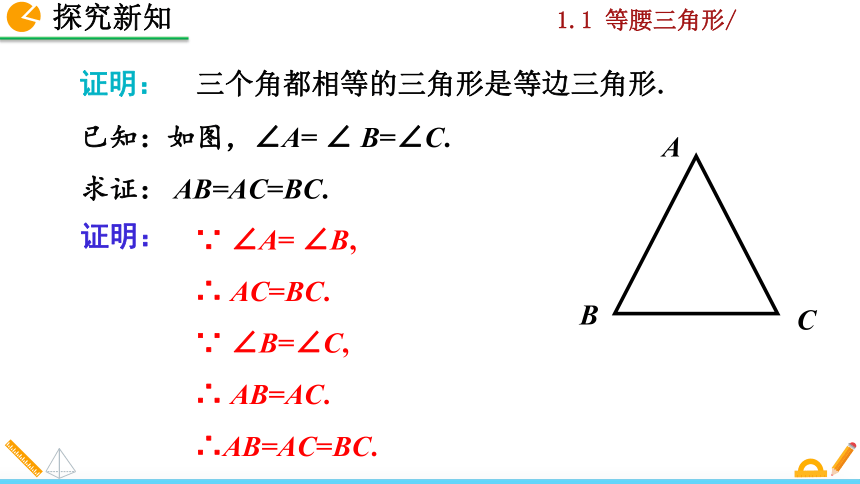
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠B,
∴ AC=BC.
∵ ∠B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
三个角都相等的三角形是等边三角形.
证明:
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
∵AB=AC , ∠A= 60 °,
∴∠B=∠C= (180°-∠A)÷2= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
证明:
有一个角是60°的等腰三角形是等边三角形.
证明:
证明完整吗?是不是还有另一种情形呢?
探究新知
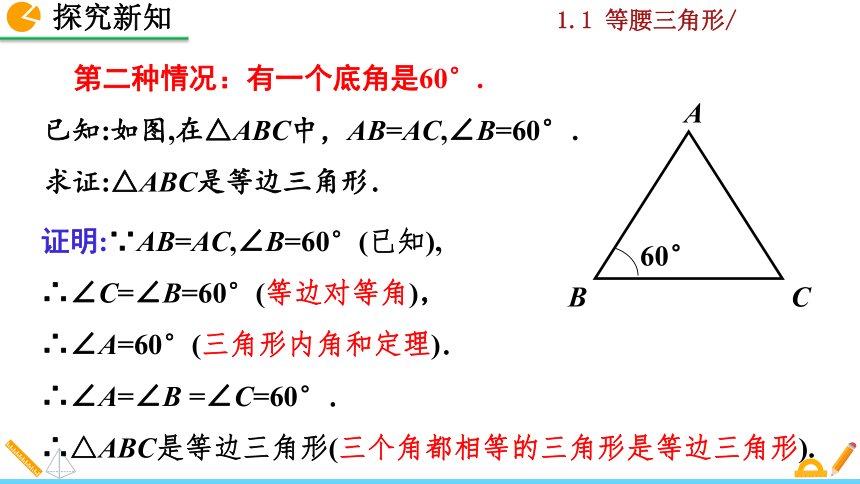
证明:∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(等边对等角),
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中,AB=AC,∠B=60°.
求证:△ABC是等边三角形.
第二种情况:有一个底角是60°.
A
C
B
60°
探究新知
1.定义:三条边都相等的三角形是等边三角形.
等边三角形的判定方法:
3.定理:有一个角等于60°的等腰三角形是等边三角形.
2.定理:三个角都相等的三角形是等边三角形.
推导过程:∵AB=BC=CA,∴ △ABC是等边三角形.
推导过程:∵∠A= ∠ B= ∠ C,∴ △ABC是等边三角形.
推导过程:∵AB=AC,∠A= 60°,∴ △ABC等边三角形.
C
B
A
结论
探究新知
等边
三角形
性质
判定的条件
三条边都相等
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是60°
三个角都相等的三角形是等边三角形
归纳总结
探究新知
三条边都相等的三角形是等边三角形
等边三角形的判定
素养考点 1
探究新知
例 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由.
解: △ODE是等边三角形.
理由:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE是等边三角形.
探究新知
(2)线段BD,DE,EC三者有什么关系?写出你的判断过程.
解:BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°,
∵OD∥AB,∴∠BOD=∠ABO=30°,
∴∠DBO=∠DOB,∴DB=DO,同理,EC=EO,
∵DE=OD=OE,∴BD=DE=EC.
方法总结
探究新知
选用等边三角形判定方法的技巧
(1)如果已知三边关系,则选用等边三角形定义来判定.
(2)若已知三角关系,则选用三角相等的三角形是等边三角形来判定.
(3)若已知是等腰三角形,则选用有一个角是60°的等腰三角形是等边三角形来判定.
巩固练习
变式训练
在△ABC中,∠A=60°,要使△ABC是等边三角形,则需添加的一个条件是 .
AB=AC或∠B=∠C
巩固练习
变式训练
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
巩固练习
变式训练
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE,
求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C=60°.
∵ AD=AE,
∴ △ADE是等腰三角形.
∴ △ADE是等边三角形.
又∵ ∠A=60°.
探究新知
知识点 2
含30°角的直角三角形的性质
操作:用两个含有30°角的三角板,你能拼成一个怎样的三角形?能拼出一个等边三角形吗 ?
猜想:在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?
30°
30°
30°
30°
30°角所对的直角边等于斜边的一半.
证明猜想:
在直角三角形中, 30°角所对的直角边等于斜边的一半.
已知:如图,在△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
A
30°
B
C
分析:证明“线段的倍、分”问题
转 化
“线段相等”问题
30°
30°
探究新知
∵ ∠ACB=90° (已知), ∴∠ACD=90°,
在△ABC与△ADC中,
BC=DC,(作图)
∠ACB=∠ACD,(已证)
AC=AC,(公共边)
∴△ABC≌△ADC(SAS) , ∴ AB=AD.
∵∠ACB=90°,∠BAC=30° (已知) , ∴∠B=60°,
∴△ABD是等边三角形, ∴BC= BD= AB.
30°
A
B
C
D
证明: 延长BC至D,使CD=BC,连接AD,
探究新知
探究新知
结论
定理 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
C
B
推导过程:Rt△ABC中
∵∠A=30°
∴ BC= AB
含30°角的直角三角形的性质
素养考点 2
探究新知
已知:如图,在△ABC中,AB=AC,∠B=15°, CD是腰AB上的高.
求证:CD= AB.
例
求证:如果等腰三角形的底角为15°,那么腰上的高是腰长的一半.
C
B
A
D
证明:∵AB=AC,∠B=15°, ∴∠B=∠ACB=15°,
∴∠DAC=∠B+∠ACB= 15°+15°=30°,
∵∠ADC=90°,∴CD= AC= AB.
探究新知
C
B
A
D
巩固练习
变式训练
如图,在△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E.如果AD=1,BC=6,那么CE等于 ( )
A.5 B.4 C.3 D.2
B
解析:∵在△ABC中,∠B=∠C=60°,
∴∠A=60°, ∴△ABC是等边三角形.
∵DE⊥AB,∴∠AED=30°,
∵AD=1,∴AE=2,
∵BC=6,∴AC=BC=6,
∴CE=AC-AE=6-2=4.
巩固练习
方法总结
含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质.
连接中考
(2020·恩施州)如图,直线l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2= .
40°
1.下列条件中,不能得到等边三角形的是 ( )
A.有两个内角是60°的三角形
B.三边都相等的三角形
C.有一个角是60°的等腰三角形
D.有两个外角相等的等腰三角形
D
课堂检测
基础巩固题
2. 三角形三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是 ( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
C
课堂检测
基础巩固题
3.如图,在正方体的两个面上画了两条对角线AB,AC,则
∠BAC等于( )
A.60° B.75°
C.90° D.135°
A
课堂检测
基础巩固题
4.在△ABC中,∠B=90°,∠C=30°,AB=3.
则AC=_____,BC=_______.
6
A
B
C
3
30°
课堂检测
5.在△ABC中,AB=AC=10 cm,BD是高,且∠ABD=30°,
则CD=________________.
5cm或15cm
基础巩固题
证明:∵∠A=30°,CD⊥AB,∠ACB=90°
∴BC= ∠B=60°,
∴BD= ∴BD=
1、已知:如图,在△ABC中,∠ACB=90°,
∠A=30°,CD⊥AB于D.
求证:BD=
D
A
C
B
30°
课堂检测
能力提升题
∴∠BCD=30°,
2、如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,
CD=4 cm,求BC的长.
证明:∵AD∥BC,∠A=120°,∴∠A+∠ABC=180°.
即∠ABC=180°-∠A=180°-120°=60°,
∴∠ABD=∠DBC=30°.
∴△BDC是直角三角形(∠BDC=90°).
又∵CD=4 cm,∴BC=2CD=2×4=8(cm).
课堂检测
能力提升题
又∵∠C=60°,
如图:△ABC是等边三角形,点D,E,F分别在BC,AB,CA边延长线上,且BE=AF=CD.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,AB=AC=BC,
∴∠EAF=∠EBD=120°,
∵BE=CD,∴BE+AB=BC+CD,即AE=BD,
课堂检测
拓广探索题
在△AEF和△BDE中,
∴△AEF≌△BDE(SAS),∴EF=ED,
同理可得△AEF≌△CFD,
∴EF=FD,∴EF=ED=FD,
∴△DEF为等边三角形.
课堂检测
课堂小结
等腰三角形的拓展
三条边都相等的三角形是等边三角形
等边三角形的判定
特殊的直角三角形的性质
三个角都相等的三角形是等边三角形
有一个角等于60°的等腰三角形是等边三角形
在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半
(第4课时)
北师大版 八年级 数学 下册
导入新知
观察下面图片,说说它们都是由什么图形组成的?
思考:上节课我们学习了等腰三角形的判定定理,那等边三角形的判定定理是什么呢?
1. 能用所学的知识证明等边三角形的判定定理.
2. 掌握含30°角的直角三角形的性质并解决有关问题.
素养目标
探究新知
知识点 1
等边三角形的判定
(2) 一个三角形满足什么条件时是等边三角形?
(3)一个等腰三角形满足什么条件时是等边三角形?
有一个角是60°的等腰三角形是等边三角形.
三条边相等的三角形是等边三角形(定 义).
三个角相等的三角形是等边三角形.
(1)等边三角形有哪些性质?
等边三角形的三条边相等,三个角相等,“三线合一”.
思考:
你能证明这些定理吗?
探究新知
A
B
C
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
∵ ∠A= ∠B,
∴ AC=BC.
∵ ∠B=∠C,
∴ AB=AC.
∴AB=AC=BC.
证明:
三个角都相等的三角形是等边三角形.
证明:
A
B
C
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
∵AB=AC , ∠A= 60 °,
∴∠B=∠C= (180°-∠A)÷2= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
证明:
有一个角是60°的等腰三角形是等边三角形.
证明:
证明完整吗?是不是还有另一种情形呢?
探究新知
证明:∵AB=AC,∠B=60°(已知),
∴∠C=∠B=60°(等边对等角),
∴∠A=60°(三角形内角和定理).
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中,AB=AC,∠B=60°.
求证:△ABC是等边三角形.
第二种情况:有一个底角是60°.
A
C
B
60°
探究新知
1.定义:三条边都相等的三角形是等边三角形.
等边三角形的判定方法:
3.定理:有一个角等于60°的等腰三角形是等边三角形.
2.定理:三个角都相等的三角形是等边三角形.
推导过程:∵AB=BC=CA,∴ △ABC是等边三角形.
推导过程:∵∠A= ∠ B= ∠ C,∴ △ABC是等边三角形.
推导过程:∵AB=AC,∠A= 60°,∴ △ABC等边三角形.
C
B
A
结论
探究新知
等边
三角形
性质
判定的条件
三条边都相等
“三线合一”,即等腰三角形顶角平分线,底边上的中线、高线互相重合
有一角是60°的等腰三角形是等边三角形
等边三角形三个内角都相等,且每个角都是60°
三个角都相等的三角形是等边三角形
归纳总结
探究新知
三条边都相等的三角形是等边三角形
等边三角形的判定
素养考点 1
探究新知
例 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由.
解: △ODE是等边三角形.
理由:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°,
∴△ODE是等边三角形.
探究新知
(2)线段BD,DE,EC三者有什么关系?写出你的判断过程.
解:BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°,
∵OD∥AB,∴∠BOD=∠ABO=30°,
∴∠DBO=∠DOB,∴DB=DO,同理,EC=EO,
∵DE=OD=OE,∴BD=DE=EC.
方法总结
探究新知
选用等边三角形判定方法的技巧
(1)如果已知三边关系,则选用等边三角形定义来判定.
(2)若已知三角关系,则选用三角相等的三角形是等边三角形来判定.
(3)若已知是等腰三角形,则选用有一个角是60°的等腰三角形是等边三角形来判定.
巩固练习
变式训练
在△ABC中,∠A=60°,要使△ABC是等边三角形,则需添加的一个条件是 .
AB=AC或∠B=∠C
巩固练习
变式训练
如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
巩固练习
变式训练
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE,
求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C=60°.
∵ AD=AE,
∴ △ADE是等腰三角形.
∴ △ADE是等边三角形.
又∵ ∠A=60°.
探究新知
知识点 2
含30°角的直角三角形的性质
操作:用两个含有30°角的三角板,你能拼成一个怎样的三角形?能拼出一个等边三角形吗 ?
猜想:在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?
30°
30°
30°
30°
30°角所对的直角边等于斜边的一半.
证明猜想:
在直角三角形中, 30°角所对的直角边等于斜边的一半.
已知:如图,在△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
A
30°
B
C
分析:证明“线段的倍、分”问题
转 化
“线段相等”问题
30°
30°
探究新知
∵ ∠ACB=90° (已知), ∴∠ACD=90°,
在△ABC与△ADC中,
BC=DC,(作图)
∠ACB=∠ACD,(已证)
AC=AC,(公共边)
∴△ABC≌△ADC(SAS) , ∴ AB=AD.
∵∠ACB=90°,∠BAC=30° (已知) , ∴∠B=60°,
∴△ABD是等边三角形, ∴BC= BD= AB.
30°
A
B
C
D
证明: 延长BC至D,使CD=BC,连接AD,
探究新知
探究新知
结论
定理 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
C
B
推导过程:Rt△ABC中
∵∠A=30°
∴ BC= AB
含30°角的直角三角形的性质
素养考点 2
探究新知
已知:如图,在△ABC中,AB=AC,∠B=15°, CD是腰AB上的高.
求证:CD= AB.
例
求证:如果等腰三角形的底角为15°,那么腰上的高是腰长的一半.
C
B
A
D
证明:∵AB=AC,∠B=15°, ∴∠B=∠ACB=15°,
∴∠DAC=∠B+∠ACB= 15°+15°=30°,
∵∠ADC=90°,∴CD= AC= AB.
探究新知
C
B
A
D
巩固练习
变式训练
如图,在△ABC中,∠B=∠C=60°,点D在AB边上,DE⊥AB,并与AC边交于点E.如果AD=1,BC=6,那么CE等于 ( )
A.5 B.4 C.3 D.2
B
解析:∵在△ABC中,∠B=∠C=60°,
∴∠A=60°, ∴△ABC是等边三角形.
∵DE⊥AB,∴∠AED=30°,
∵AD=1,∴AE=2,
∵BC=6,∴AC=BC=6,
∴CE=AC-AE=6-2=4.
巩固练习
方法总结
含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据,如果问题中出现探究线段倍分关系的结论时,要联想此性质.
连接中考
(2020·恩施州)如图,直线l1∥l2,点A在直线l1上,点B在直线l2上,AB=BC,∠C=30°,∠1=80°,则∠2= .
40°
1.下列条件中,不能得到等边三角形的是 ( )
A.有两个内角是60°的三角形
B.三边都相等的三角形
C.有一个角是60°的等腰三角形
D.有两个外角相等的等腰三角形
D
课堂检测
基础巩固题
2. 三角形三边长分别为a,b,c,它们满足(a-b)2+|b-c|=0,则该三角形是 ( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
C
课堂检测
基础巩固题
3.如图,在正方体的两个面上画了两条对角线AB,AC,则
∠BAC等于( )
A.60° B.75°
C.90° D.135°
A
课堂检测
基础巩固题
4.在△ABC中,∠B=90°,∠C=30°,AB=3.
则AC=_____,BC=_______.
6
A
B
C
3
30°
课堂检测
5.在△ABC中,AB=AC=10 cm,BD是高,且∠ABD=30°,
则CD=________________.
5cm或15cm
基础巩固题
证明:∵∠A=30°,CD⊥AB,∠ACB=90°
∴BC= ∠B=60°,
∴BD= ∴BD=
1、已知:如图,在△ABC中,∠ACB=90°,
∠A=30°,CD⊥AB于D.
求证:BD=
D
A
C
B
30°
课堂检测
能力提升题
∴∠BCD=30°,
2、如图,AD∥BC,BD平分∠ABC,∠A=120°,∠C=60°,
CD=4 cm,求BC的长.
证明:∵AD∥BC,∠A=120°,∴∠A+∠ABC=180°.
即∠ABC=180°-∠A=180°-120°=60°,
∴∠ABD=∠DBC=30°.
∴△BDC是直角三角形(∠BDC=90°).
又∵CD=4 cm,∴BC=2CD=2×4=8(cm).
课堂检测
能力提升题
又∵∠C=60°,
如图:△ABC是等边三角形,点D,E,F分别在BC,AB,CA边延长线上,且BE=AF=CD.
求证:△DEF是等边三角形.
证明:∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,AB=AC=BC,
∴∠EAF=∠EBD=120°,
∵BE=CD,∴BE+AB=BC+CD,即AE=BD,
课堂检测
拓广探索题
在△AEF和△BDE中,
∴△AEF≌△BDE(SAS),∴EF=ED,
同理可得△AEF≌△CFD,
∴EF=FD,∴EF=ED=FD,
∴△DEF为等边三角形.
课堂检测
课堂小结
等腰三角形的拓展
三条边都相等的三角形是等边三角形
等边三角形的判定
特殊的直角三角形的性质
三个角都相等的三角形是等边三角形
有一个角等于60°的等腰三角形是等边三角形
在直角三角形中, 如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
