北师大版八年级数学下册1.3 线段的垂直平分线课件(第2课时 30张)
文档属性
| 名称 | 北师大版八年级数学下册1.3 线段的垂直平分线课件(第2课时 30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 527.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:06:43 | ||
图片预览







文档简介
1.3 线段的垂直平分线
(第2课时)
北师大版 八年级 数学 下册
导入新知
A
B
C
D
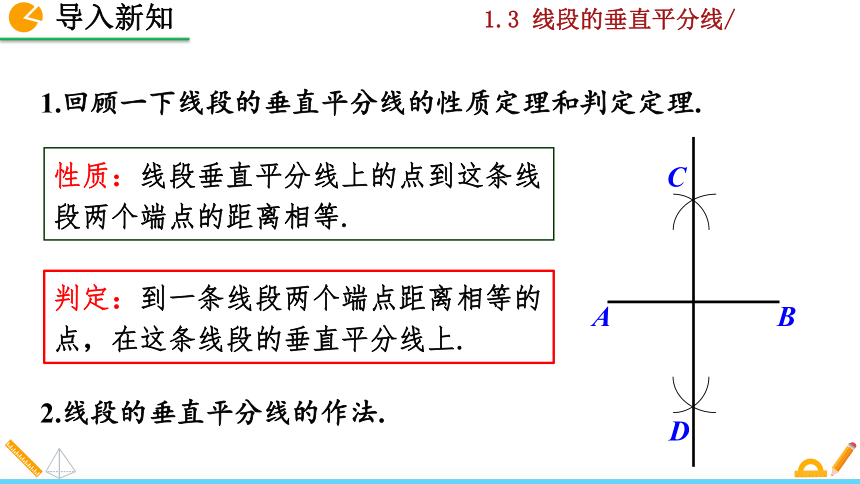
1.回顾一下线段的垂直平分线的性质定理和判定定理.
2.线段的垂直平分线的作法.
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
1. 理解并掌握三角形三边的垂直平分线的性质.
2. 能够运用三角形三边的垂直平分线的性质解决实际问题.
素养目标
3. 能够利用尺规作已知底边及底边上的高的等腰三角形.
画一画:
利用尺规作三角形三条边的垂直平分线,完成之后你发现了什么?
知识点1
三角形三边的垂直平分线的性质
发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.
探究新知
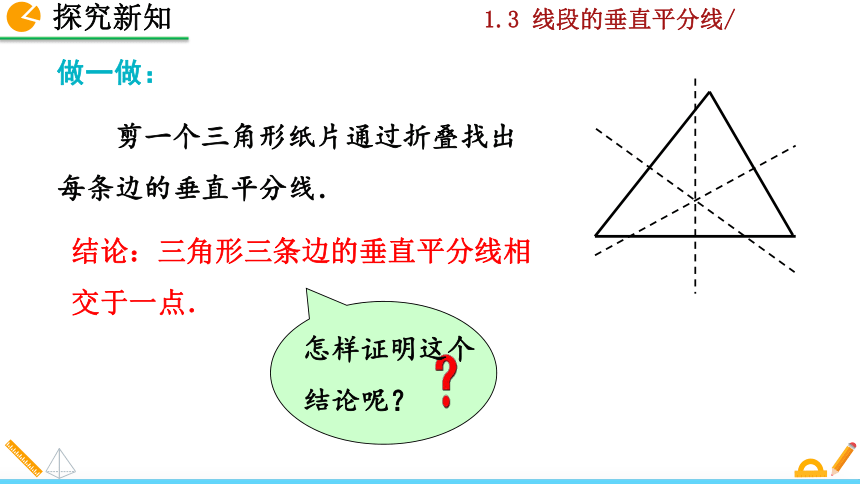
剪一个三角形纸片通过折叠找出每条边的垂直平分线.
结论:三角形三条边的垂直平分线相交于一点.
怎样证明这个结论呢?
探究新知
做一做:
点拨:要证明三条直线相交于一点,只要证明其中两条直线的交点在第三条直线上即可.
思路可表示如下:
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
l是AB的垂直平分线
m是BC的垂直平分线
PA=PB
PB=PC
PA=PC
点P在AC的垂直平分线上
结论证明:
探究新知
探究新知
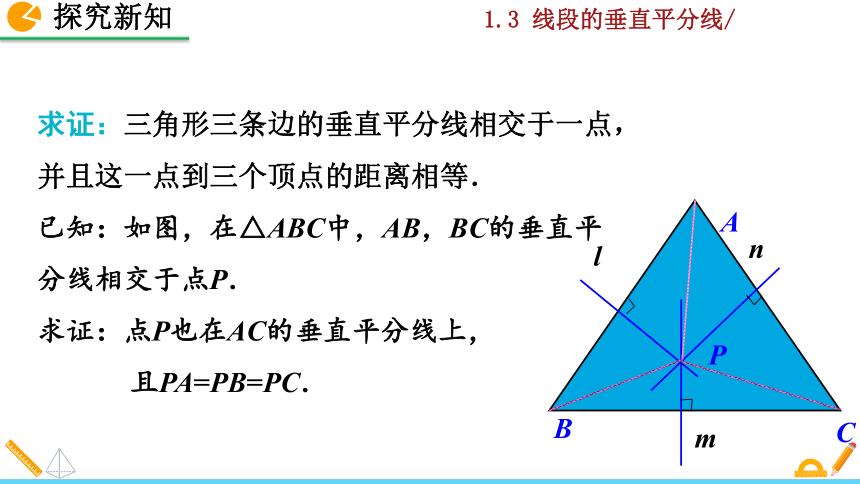
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P.
求证:点P也在AC的垂直平分线上,
且PA=PB=PC.
B
C
A
P
l
n
m
探究新知
证明:∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC (线段垂直平分线上 的点到线段两端距离相等).
同理,PB=PC,∴ PA=PB=PC,
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的
垂直平分线上).
即边AC的垂直平分线经过点P.
B
C
A
P
l
n
m
探究新知
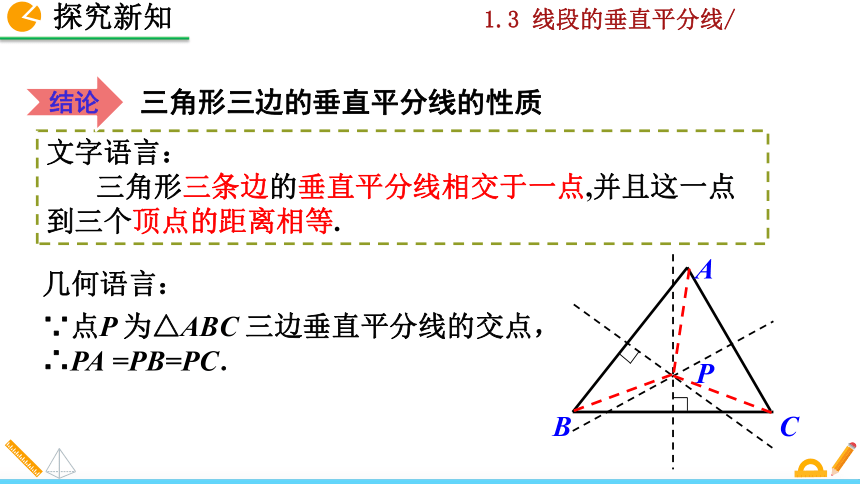
文字语言:
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
三角形三边的垂直平分线的性质
结论
几何语言:
∵点P 为△ABC 三边垂直平分线的交点,
∴PA =PB=PC.
A
B
C
P
三角形三边的垂直平分线的性质
素养考点 1
探究新知
如果三角形三条边的垂直平分线的交点在三角形的
外部,那么这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
例
C
巩固练习
变式训练
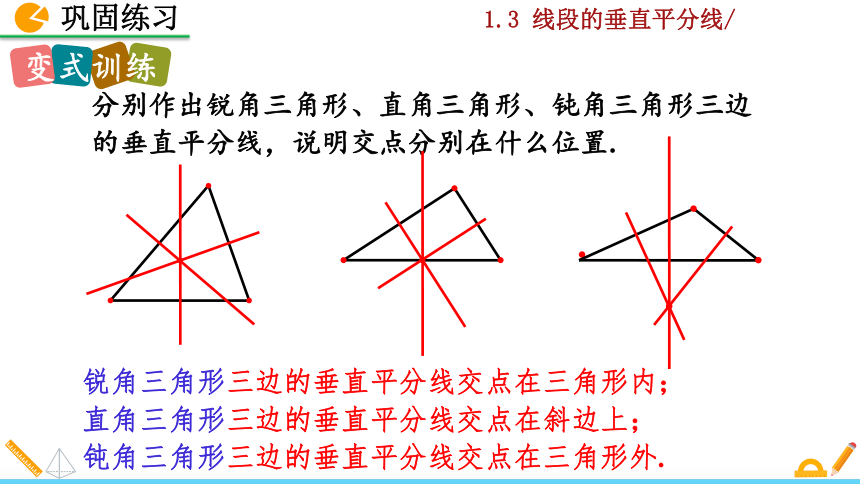
分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
探究新知
做一做:
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
知识点2
尺规作图
探究新知
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
能作出无数个这样的三角形,它们并不全等.
探究新知
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几个?所作出的三角形都全等吗?
这样的等腰三角形有无数多个.
根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
探究新知
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
探究新知
已知一个等腰三角形的底及底边上的高,求作这个等腰三角形.
已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
a
h
N
M
D
C
B
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
探究新知
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
尺规作图
素养考点
探究新知
作法:
①以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
②作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
A
B
C
P
l
例
已知直线l和l上一点P,利用尺规作 l 的垂线,使它经过点P.
巩固练习
变式训练
已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
B
A
作法:
①先以点P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于点A,B.
②分别以A、B为圆心,大于线段AB长度的一半为半径作圆,相交于C、D两点.
③过两交点作直线 l ',此直线为
l 过点P的垂线.
P
C
D
连接中考
(2020·宜昌)如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A
A. l是线段EH的垂直平分线
B. l是线段EQ的垂直平分线
C. l是线段FH的垂直平分线
D. EH是l的垂直平分线
1. 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70°
C.60° D.50°
C
B
A
D
E
C
课堂检测
基础巩固题
2. 已知:如图,在△ABC中,边AB,BC的垂直平分线交于点P.则下列结论一定成立的个数为( )
①PA=PB=PC.
②点P在AC的垂直平分线上.
③∠BPC=90°+ ∠BAC.
④∠BAP=∠CAP.
A.1个 B.2个 C.3个 D.4个
B
课堂检测
基础巩固题
3. 如图,有A,B,C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A.AC,BC两边高线的交点处
B.AC,BC两边垂直平分线的交点处
C.AC,BC两边中线的交点处
D.∠A,∠B两内角平分线的交点处
B
课堂检测
基础巩固题
4.如图,在△ABC中,点D是边AB,BC的垂直平分线交点,连接AD并延长交BC于点E,若∠AEC=3∠BAE=3α,则∠CAE=____________(用含α的式子表示).?
90°-2α
课堂检测
基础巩固题
C
5.如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.7 B.14
C.17 D.20
课堂检测
基础巩固题
1.如图,在△ABC中,点D为BC上一点,连接AD,点E在线段AD上,并且∠1=∠2,∠3=∠4,求证:AD垂直平分BC.
证明:∵∠1=∠2,∠3=∠4,
∴EB=EC,且∠1+∠3=∠2+∠4,
即∠ABC=∠ACB,∴AB=AC,
∴A与E都在线段BC的垂直平分线上,
则AD垂直平分BC.
课堂检测
能力提升题
2.如图,在△ABC中,D为BC的中点,E、F分别是AB、AC上的点,且DE⊥DF.求证:BE+CF>EF.
证明:延长FD到G,使DG=DF.连接EG、BG.
在△CDF和△BDG中,CD=BD,∠CDF=∠BDG,DF=DG,
∴△CDF≌△BDG(SAS),∴BG=CF.
∵DE⊥DF,DF=DG,
∴EG=EF.在△BEG中,BE+BG>EG,
∴BE+CF>EF.
课堂检测
能力提升题
如图,在△ABC中,AC边的垂直平分线DM交AC于点D,BC边
的垂直平分线EN交BC于点E,DM与EN相交于点F .
解:∵DM是AC边的垂直平分线,∴MA=MC,
∵EN是BC边的垂直平分线,∴NB=NC,
AB=AM+MN+NB=MC+MN+NC=△CMN的周长=20 cm.
(1)若△CMN的周长为20 cm,求AB的长.
课堂检测
拓广探索题
解:∵MD⊥AC,NE⊥BC,∴∠ACB=180°-∠MFN=110°,
∴∠A+∠B=70°,
∵MA=MC,NB=NC,∴∠MCA=∠A,∠NCB=∠B,
∴∠MCN=40°.
(2)若∠MFN=70°,求∠MCN的度数.
课堂检测
课堂小结
线段的垂直平分线
三角形三边的垂直平分线的性质
尺规作图
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等
(第2课时)
北师大版 八年级 数学 下册
导入新知
A
B
C
D
1.回顾一下线段的垂直平分线的性质定理和判定定理.
2.线段的垂直平分线的作法.
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
1. 理解并掌握三角形三边的垂直平分线的性质.
2. 能够运用三角形三边的垂直平分线的性质解决实际问题.
素养目标
3. 能够利用尺规作已知底边及底边上的高的等腰三角形.
画一画:
利用尺规作三角形三条边的垂直平分线,完成之后你发现了什么?
知识点1
三角形三边的垂直平分线的性质
发现:三角形三边的垂直平分线交于一点.这一点到三角形三个顶点的距离相等.
探究新知
剪一个三角形纸片通过折叠找出每条边的垂直平分线.
结论:三角形三条边的垂直平分线相交于一点.
怎样证明这个结论呢?
探究新知
做一做:
点拨:要证明三条直线相交于一点,只要证明其中两条直线的交点在第三条直线上即可.
思路可表示如下:
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
l是AB的垂直平分线
m是BC的垂直平分线
PA=PB
PB=PC
PA=PC
点P在AC的垂直平分线上
结论证明:
探究新知
探究新知
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P.
求证:点P也在AC的垂直平分线上,
且PA=PB=PC.
B
C
A
P
l
n
m
探究新知
证明:∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC (线段垂直平分线上 的点到线段两端距离相等).
同理,PB=PC,∴ PA=PB=PC,
∴点P在BC的垂直平分线上
(到线段两端距离相等的点在线段的
垂直平分线上).
即边AC的垂直平分线经过点P.
B
C
A
P
l
n
m
探究新知
文字语言:
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
三角形三边的垂直平分线的性质
结论
几何语言:
∵点P 为△ABC 三边垂直平分线的交点,
∴PA =PB=PC.
A
B
C
P
三角形三边的垂直平分线的性质
素养考点 1
探究新知
如果三角形三条边的垂直平分线的交点在三角形的
外部,那么这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
例
C
巩固练习
变式训练
分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边上;
钝角三角形三边的垂直平分线交点在三角形外.
探究新知
做一做:
(1)已知三角形的一条边及这条边上的高,你能作出三角形吗?如果能,能作几个?所作出的三角形都全等吗?
知识点2
尺规作图
探究新知
已知:三角形的一条边a和这边上的高h.
求作:△ABC,使BC=a,BC边上的高为h.
A1
D
C
B
A
a
h
(D)
C
B
A
a
h
A1
D
C
B
A
a
h
A1
能作出无数个这样的三角形,它们并不全等.
探究新知
(2)已知等腰三角形的底边,你能用尺规作出等腰三角形吗?如果能,能作几个?所作出的三角形都全等吗?
这样的等腰三角形有无数多个.
根据线段垂直平分线上的点到线段两个端点的距离相等,只要作底边的垂直平分线,取它上面除底边的中点外的任意一点,和底边的两个端点相连接,都可以得到一个等腰三角形.
如图所示,这些三角形不都全等.
探究新知
(3)已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
探究新知
已知一个等腰三角形的底及底边上的高,求作这个等腰三角形.
已知:线段a,h.
求作:△ABC,使AB=AC,BC=a,高AD=h.
a
h
N
M
D
C
B
A
作法:
1.作BC=a;
2.作线段BC的垂直平分线MN交BC于D点;
3.以D为圆心,h长为半径作弧交MN于A点;
4.连接AB,AC.
△ABC就是所求作的三角形.
探究新知
已知:直线 l 和 l 上一点P.
求作:PC⊥ l .
尺规作图
素养考点
探究新知
作法:
①以点P为圆心,以任意长为半径作弧,与直线 l 相交于点A和B.
②作线段AB的垂直平分线PC.
直线PC就是所求 l 的垂线.
A
B
C
P
l
例
已知直线l和l上一点P,利用尺规作 l 的垂线,使它经过点P.
巩固练习
变式训练
已知直线 l 和线外一点P,利用尺规作 l 的垂线,使它经过点P.
B
A
作法:
①先以点P为圆心,大于点P到直线 l 的垂直距离R为半径作圆,交直线 l 于点A,B.
②分别以A、B为圆心,大于线段AB长度的一半为半径作圆,相交于C、D两点.
③过两交点作直线 l ',此直线为
l 过点P的垂线.
P
C
D
连接中考
(2020·宜昌)如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A
A. l是线段EH的垂直平分线
B. l是线段EQ的垂直平分线
C. l是线段FH的垂直平分线
D. EH是l的垂直平分线
1. 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
A.80° B.70°
C.60° D.50°
C
B
A
D
E
C
课堂检测
基础巩固题
2. 已知:如图,在△ABC中,边AB,BC的垂直平分线交于点P.则下列结论一定成立的个数为( )
①PA=PB=PC.
②点P在AC的垂直平分线上.
③∠BPC=90°+ ∠BAC.
④∠BAP=∠CAP.
A.1个 B.2个 C.3个 D.4个
B
课堂检测
基础巩固题
3. 如图,有A,B,C三个居民小区,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在 ( )
A.AC,BC两边高线的交点处
B.AC,BC两边垂直平分线的交点处
C.AC,BC两边中线的交点处
D.∠A,∠B两内角平分线的交点处
B
课堂检测
基础巩固题
4.如图,在△ABC中,点D是边AB,BC的垂直平分线交点,连接AD并延长交BC于点E,若∠AEC=3∠BAE=3α,则∠CAE=____________(用含α的式子表示).?
90°-2α
课堂检测
基础巩固题
C
5.如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.7 B.14
C.17 D.20
课堂检测
基础巩固题
1.如图,在△ABC中,点D为BC上一点,连接AD,点E在线段AD上,并且∠1=∠2,∠3=∠4,求证:AD垂直平分BC.
证明:∵∠1=∠2,∠3=∠4,
∴EB=EC,且∠1+∠3=∠2+∠4,
即∠ABC=∠ACB,∴AB=AC,
∴A与E都在线段BC的垂直平分线上,
则AD垂直平分BC.
课堂检测
能力提升题
2.如图,在△ABC中,D为BC的中点,E、F分别是AB、AC上的点,且DE⊥DF.求证:BE+CF>EF.
证明:延长FD到G,使DG=DF.连接EG、BG.
在△CDF和△BDG中,CD=BD,∠CDF=∠BDG,DF=DG,
∴△CDF≌△BDG(SAS),∴BG=CF.
∵DE⊥DF,DF=DG,
∴EG=EF.在△BEG中,BE+BG>EG,
∴BE+CF>EF.
课堂检测
能力提升题
如图,在△ABC中,AC边的垂直平分线DM交AC于点D,BC边
的垂直平分线EN交BC于点E,DM与EN相交于点F .
解:∵DM是AC边的垂直平分线,∴MA=MC,
∵EN是BC边的垂直平分线,∴NB=NC,
AB=AM+MN+NB=MC+MN+NC=△CMN的周长=20 cm.
(1)若△CMN的周长为20 cm,求AB的长.
课堂检测
拓广探索题
解:∵MD⊥AC,NE⊥BC,∴∠ACB=180°-∠MFN=110°,
∴∠A+∠B=70°,
∵MA=MC,NB=NC,∴∠MCA=∠A,∠NCB=∠B,
∴∠MCN=40°.
(2)若∠MFN=70°,求∠MCN的度数.
课堂检测
课堂小结
线段的垂直平分线
三角形三边的垂直平分线的性质
尺规作图
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
