北师大版八年级数学下册1.4 角平分线课件(第2课时 31张)
文档属性
| 名称 | 北师大版八年级数学下册1.4 角平分线课件(第2课时 31张) |  | |
| 格式 | pptx | ||
| 文件大小 | 529.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:06:45 | ||
图片预览





文档简介
1.4 角平分线
(第2课时)
北师大版 八年级 数学 下册
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
导入新知
A
B
C
1.会证明和运用“三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等”.
2.经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.
素养目标
探究新知
知识点
三角形的内角平分线
画一画:
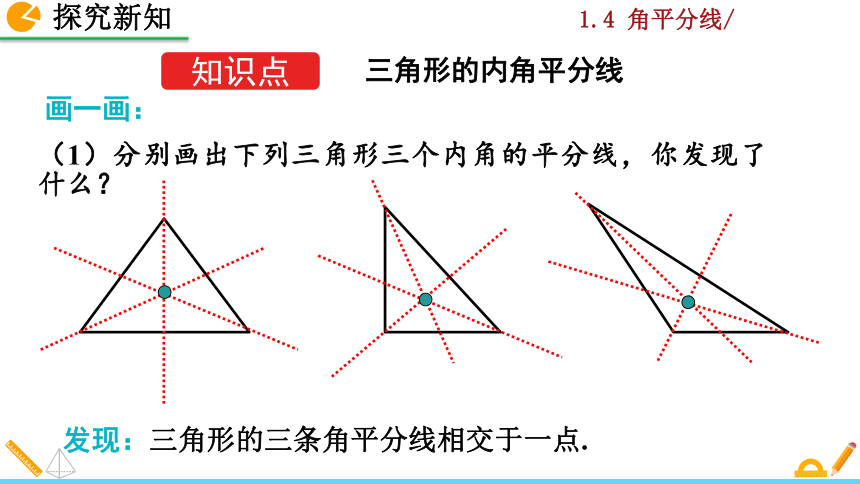
(1)分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点.
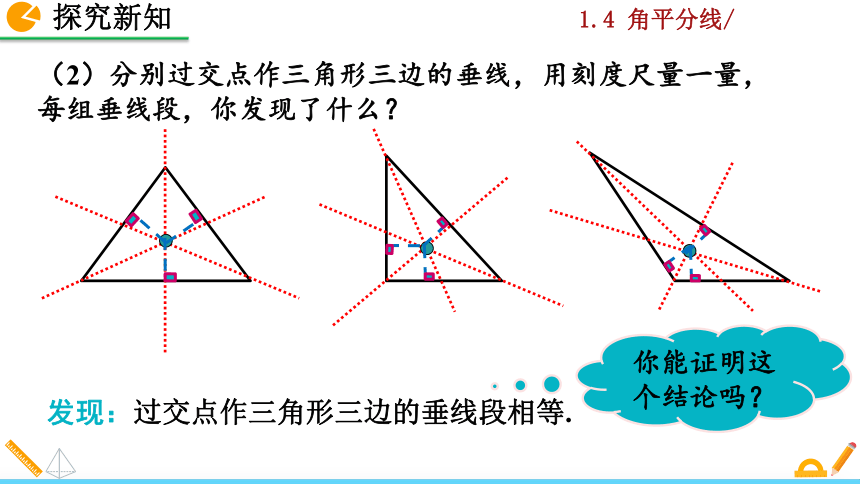
(2)分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
探究新知
做一做:
剪一个三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你是否发现同样的结论?与同伴交流.
结论:三角形的三条角平分线相交于一点.
怎样证明这个结论呢?
探究新知
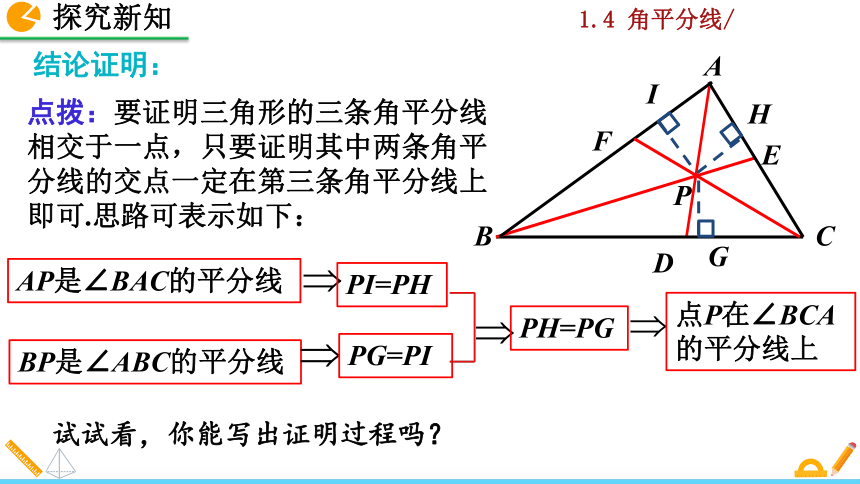
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你能写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
结论证明:
探究新知
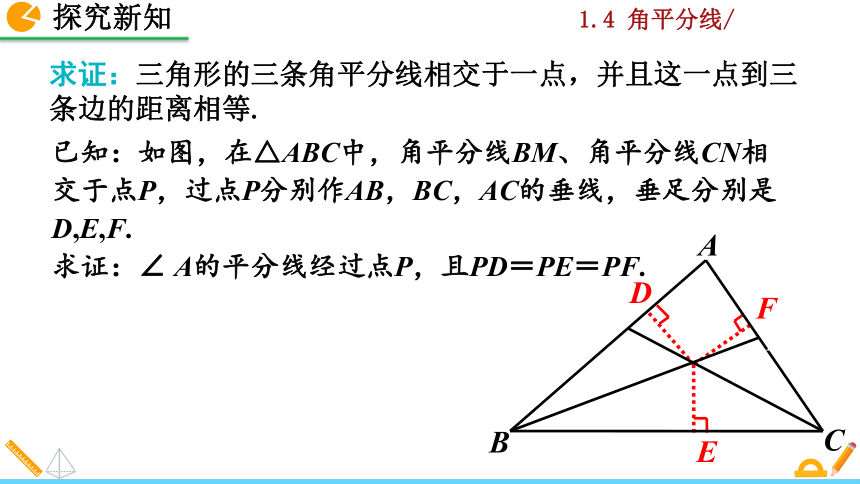
已知:如图,在△ABC中,角平分线BM、角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别是D,E,F.
求证:∠ A的平分线经过点P,且PD=PE=PF.
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
D
E
F
M
N
C
B
A
P
探究新知
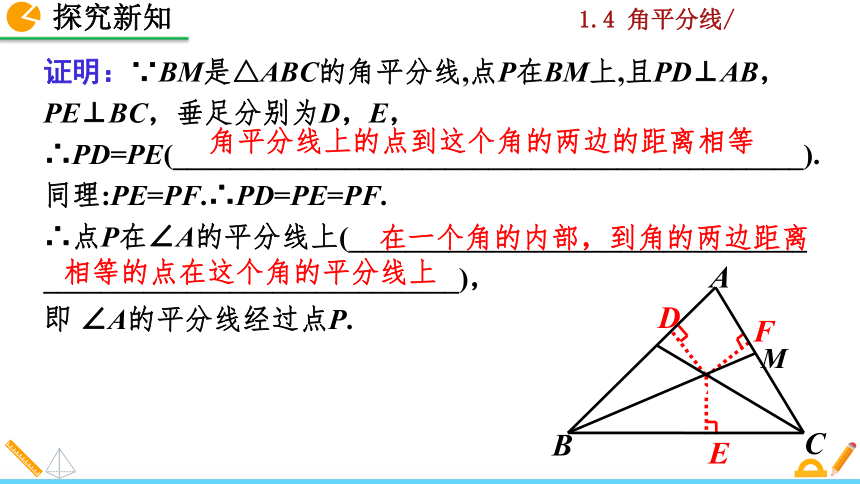
证明:∵BM是△ABC的角平分线,点P在BM上,且PD⊥AB,PE⊥BC,垂足分别为D,E,
∴PD=PE(____________________________________________).?
同理:PE=PF.∴PD=PE=PF.
∴点P在∠A的平分线上(________________________________ _____________________________),
即 ∠A的平分线经过点P.
角平分线上的点到这个角的两边的距离相等
在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D
E
F
M
N
C
B
A
P
探究新知
探究新知
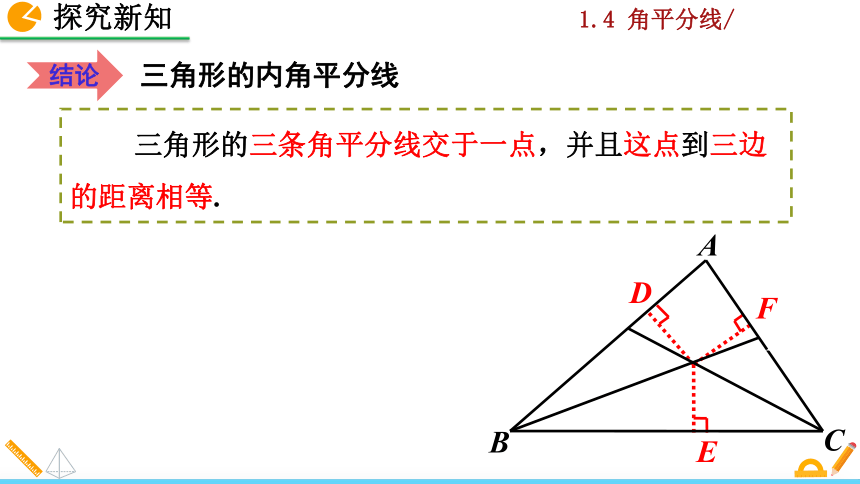
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
三角形的内角平分线
结论
D
E
F
M
N
C
B
A
P
在一块三角形的草坪上建一座凉亭,要使凉亭到草坪
三边的距离相等,凉亭的位置应选在( )
A.三角形的三条中线的交点处
B.三角形的三边的垂直平分线的交点处
C.三角形的三条角平分线的交点处
D.三角形的三条高所在直线的交点处
C
探究新知
做一做:
探究新知
三角形三边的垂直平分线和三条角平分线的区别
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形_______一点?
交于三角形
_______一点?
钝角三角形
交于三角形_______一点?
直角三角形
交于斜边的_________?
交点性质
到三角形_____________的距离相等?
到三角形_____
____的距离相等?
内
外
中点
内
三个顶点
三
边
总结:
三角形的内角平分线
素养考点
探究新知
解:
如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
例1
∵AD是△ABC的角平分线, DC⊥AC,
DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
E
D
A
B
C
(2)求证:AB=AC+CD.
由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
探究新知
证明:
E
D
A
B
C
如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
解:点O到△ABC三边的距离和为12.
巩固练习
变式训练
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
连接OC,
探究新知
解:
M
E
N
A
B
C
P
O
D
探究新知
如图,在△ABC中,∠ACB=90°,AO,CO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.
例2
解:连接OB,过O作OE⊥AB于E,OF⊥BC于F,
∵AO平分∠BAC,CO平分∠ACB,OE⊥AB,OF⊥BC,OD⊥AC,
∴OE=OD=OF, 设OE=OF=OD=R,
在△ABC中,∠ACB=90°,AB=10,BC=8,
由勾股定理得:AC=6,
探究新知
∵S△ABC=S△ABO+S△ACO+S△BCO,
∴ AC·BC= AB·OE+ AC·OD+ BC·OF,
∴6×8=10R+6R+8R,解得:R=2,
∴OD的长为2.
方法总结
探究新知
1.三角形三个内角平分线的交点与三角形三个顶点的连线把原三角形分割成了三个小三角形,利用三个小三角形面积之和等于原三角形的面积,即等积法即可求出交点到三边的距离.
2.已知角平分线上的点,要利用角平分线性质定理寻找线段相等关系,有时可结合全等三角形、直角三角形来求解.
如图所示,在△ABC中,∠B=90°,AB=7,BC=24,AC=25.
(1)△ABC内是否存在一点到各边的距离相等?如果存在,请作出这一点,并说明理由;
巩固练习
变式训练
解:如图,作∠BAC、∠ACB的平分线,它们的交点P即为符合要求的点.
作PE⊥AB,PF⊥BC,PG⊥AC,
垂足分别为E、F、G.
∵AP是∠BAC的平分线,∴PE=PG.
∵CP是∠ACB的平分线,∴PF=PG.
∴PE=PF=PG;
(2)求这点到各边的距离.
巩固练习
解:连接BP.设PE=PF=PG=x.
∵S△ABC=S△APB+S△BPC+S△APC,
∴0.5AB·BC=0.5AB·x+0.5BC·x+0.5AC·x.
∴7×24=(7+24+25)x.
解得x=3.
即这点到各边的距离为3.
连接中考
(2020·怀化)在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A
A.3 B.1.5
C.2 D.6
1. △ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线相交于点O,那么下列说法不正确的是 ( )
A.点O一定在△ABC的内部
B.∠C的平分线一定经过点O
C.点O到△ABC三边的距离一定相等
D.点O到△ABC的三个顶点的距离一定相等
D
课堂检测
基础巩固题
2. 如图,在Rt△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A
A.110° B.120°
C.130° D.140°
课堂检测
基础巩固题
3.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
B
课堂检测
基础巩固题
4. 如图, O是△ABC的角平分线的交点,△ABC的面积为2,周长为4,则点O到BC的距离为( )
A.1 B.2
C.3 D.无法确定
A
课堂检测
基础巩固题
F
A
E
D
B
1、已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF.
求证:CF=EB.
证明:∵AD平分∠CAB,
DE⊥AB,∠C=90°(已知),
∴ CD=DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
CD=ED(已证),
DF=DB (已知),
∴ Rt△CDF≌Rt△EDB (HL).
∴ CF=EB(全等三角形的对应边相等).
C
课堂检测
能力提升题
2、如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
课堂检测
能力提升题
P1
P2
P3
P4
l1
l2
l3
课堂检测
如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于 ( )
A.1∶1∶1 B.1∶2∶3
C.2∶3∶4 D.3∶4∶5
C
课堂检测
拓广探索题
课堂小结
三角形内角平分线的性质
性质:三角形的三条角平分线交于一点,并且这一点到三条边的距离相等.
应用:位置的选择问题.
(第2课时)
北师大版 八年级 数学 下册
在一个三角形居住区内修有一个学校P,P到AB、BC、CA三边的距离都相等,请在三角形居住区内标出学校P的位置,P在何处?
导入新知
A
B
C
1.会证明和运用“三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等”.
2.经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.
素养目标
探究新知
知识点
三角形的内角平分线
画一画:
(1)分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点.
(2)分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
探究新知
做一做:
剪一个三角形纸片,通过折叠找出每个角的角平分线,观察这三条角平分线,你是否发现同样的结论?与同伴交流.
结论:三角形的三条角平分线相交于一点.
怎样证明这个结论呢?
探究新知
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你能写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
结论证明:
探究新知
已知:如图,在△ABC中,角平分线BM、角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别是D,E,F.
求证:∠ A的平分线经过点P,且PD=PE=PF.
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
D
E
F
M
N
C
B
A
P
探究新知
证明:∵BM是△ABC的角平分线,点P在BM上,且PD⊥AB,PE⊥BC,垂足分别为D,E,
∴PD=PE(____________________________________________).?
同理:PE=PF.∴PD=PE=PF.
∴点P在∠A的平分线上(________________________________ _____________________________),
即 ∠A的平分线经过点P.
角平分线上的点到这个角的两边的距离相等
在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D
E
F
M
N
C
B
A
P
探究新知
探究新知
三角形的三条角平分线交于一点,并且这点到三边的距离相等.
三角形的内角平分线
结论
D
E
F
M
N
C
B
A
P
在一块三角形的草坪上建一座凉亭,要使凉亭到草坪
三边的距离相等,凉亭的位置应选在( )
A.三角形的三条中线的交点处
B.三角形的三边的垂直平分线的交点处
C.三角形的三条角平分线的交点处
D.三角形的三条高所在直线的交点处
C
探究新知
做一做:
探究新知
三角形三边的垂直平分线和三条角平分线的区别
三边垂直平分线
三条角平分线
三角形
锐角三角形
交于三角形_______一点?
交于三角形
_______一点?
钝角三角形
交于三角形_______一点?
直角三角形
交于斜边的_________?
交点性质
到三角形_____________的距离相等?
到三角形_____
____的距离相等?
内
外
中点
内
三个顶点
三
边
总结:
三角形的内角平分线
素养考点
探究新知
解:
如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
例1
∵AD是△ABC的角平分线, DC⊥AC,
DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
E
D
A
B
C
(2)求证:AB=AC+CD.
由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
探究新知
证明:
E
D
A
B
C
如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
解:点O到△ABC三边的距离和为12.
巩固练习
变式训练
M
E
N
A
B
C
P
O
D
(2)若△ABC的周长为32,求△ABC的面积.
连接OC,
探究新知
解:
M
E
N
A
B
C
P
O
D
探究新知
如图,在△ABC中,∠ACB=90°,AO,CO分别平分∠BAC和∠ACB,OD⊥AC于D.若AB=10,BC=8,试求线段OD的长度.
例2
解:连接OB,过O作OE⊥AB于E,OF⊥BC于F,
∵AO平分∠BAC,CO平分∠ACB,OE⊥AB,OF⊥BC,OD⊥AC,
∴OE=OD=OF, 设OE=OF=OD=R,
在△ABC中,∠ACB=90°,AB=10,BC=8,
由勾股定理得:AC=6,
探究新知
∵S△ABC=S△ABO+S△ACO+S△BCO,
∴ AC·BC= AB·OE+ AC·OD+ BC·OF,
∴6×8=10R+6R+8R,解得:R=2,
∴OD的长为2.
方法总结
探究新知
1.三角形三个内角平分线的交点与三角形三个顶点的连线把原三角形分割成了三个小三角形,利用三个小三角形面积之和等于原三角形的面积,即等积法即可求出交点到三边的距离.
2.已知角平分线上的点,要利用角平分线性质定理寻找线段相等关系,有时可结合全等三角形、直角三角形来求解.
如图所示,在△ABC中,∠B=90°,AB=7,BC=24,AC=25.
(1)△ABC内是否存在一点到各边的距离相等?如果存在,请作出这一点,并说明理由;
巩固练习
变式训练
解:如图,作∠BAC、∠ACB的平分线,它们的交点P即为符合要求的点.
作PE⊥AB,PF⊥BC,PG⊥AC,
垂足分别为E、F、G.
∵AP是∠BAC的平分线,∴PE=PG.
∵CP是∠ACB的平分线,∴PF=PG.
∴PE=PF=PG;
(2)求这点到各边的距离.
巩固练习
解:连接BP.设PE=PF=PG=x.
∵S△ABC=S△APB+S△BPC+S△APC,
∴0.5AB·BC=0.5AB·x+0.5BC·x+0.5AC·x.
∴7×24=(7+24+25)x.
解得x=3.
即这点到各边的距离为3.
连接中考
(2020·怀化)在Rt△ABC中,∠B=90°,AD平分∠BAC,交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A
A.3 B.1.5
C.2 D.6
1. △ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线相交于点O,那么下列说法不正确的是 ( )
A.点O一定在△ABC的内部
B.∠C的平分线一定经过点O
C.点O到△ABC三边的距离一定相等
D.点O到△ABC的三个顶点的距离一定相等
D
课堂检测
基础巩固题
2. 如图,在Rt△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A
A.110° B.120°
C.130° D.140°
课堂检测
基础巩固题
3.如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是( )
A.P为∠A,∠B两角平分线的交点
B.P为∠A的平分线与AB的垂直平分线的交点
C.P为AC,AB两边上的高的交点
D.P为AC,AB两边的垂直平分线的交点
B
课堂检测
基础巩固题
4. 如图, O是△ABC的角平分线的交点,△ABC的面积为2,周长为4,则点O到BC的距离为( )
A.1 B.2
C.3 D.无法确定
A
课堂检测
基础巩固题
F
A
E
D
B
1、已知:如图,△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB于E,F在AC上,BD=DF.
求证:CF=EB.
证明:∵AD平分∠CAB,
DE⊥AB,∠C=90°(已知),
∴ CD=DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
CD=ED(已证),
DF=DB (已知),
∴ Rt△CDF≌Rt△EDB (HL).
∴ CF=EB(全等三角形的对应边相等).
C
课堂检测
能力提升题
2、如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
课堂检测
能力提升题
P1
P2
P3
P4
l1
l2
l3
课堂检测
如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于 ( )
A.1∶1∶1 B.1∶2∶3
C.2∶3∶4 D.3∶4∶5
C
课堂检测
拓广探索题
课堂小结
三角形内角平分线的性质
性质:三角形的三条角平分线交于一点,并且这一点到三条边的距离相等.
应用:位置的选择问题.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
