北师大版八年级数学下册4.1 因式分解课件(29张)
文档属性
| 名称 | 北师大版八年级数学下册4.1 因式分解课件(29张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:49:36 | ||
图片预览








文档简介
4.1 因式分解
北师大版 八年级 数学 下册
1. 630可以被哪些整数整除?
导入新知
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
解决这个问题,需要对630进行分解质因数
????????????=????×????????×????×????
?
(1)单项式×单项式:3a?4b= .
(2)单项式×多项式:am+n= .
(3)多项式×多项式:a+bm+n= .
?
2.整式乘法类型
导入新知
12ab
?
am+an
?
am+an+bm+bn
?
(1)平方差公式: (a+b)(a?b?) = .
(2)完全平方公式: (a±b)2= .
?
3.特殊的整式乘法公式
a2±2ab+b2
a2-b2
1. 理解掌握因式分解的意义,会判断一个变形是否为因式分解.
2. 理解因式分解与整式乘法之间的联系与区别.
素养目标
1.?????????????????????能被100整除吗?
?
探究新知
知识点 1
因式分解的定义
小明是这样做的:
??????????????????????????
=????????×?????????????????????×????
=?????????????????????????
=????????×????????????????
=????????×????????×????????????.
所以,?????????????????????能被100整除.
?
你知道每一步的依据吗?
??????????????????????????
=????????×?????????????????????×????
=?????????????????????????
=????????×????????????????
=????????×????????×????????????.
所以,?????????????????????能被100整除.
?
?????????????????????还能被哪些正整数整除?
?
还能被98,99整除
探究新知
在这里,解决问题的关键是把一个数式
化成了几个数的积的形式.
2.将99换成其他任意一个大于1的整数,上述结论仍然成立吗?
探究新知
用a表示任意一个大于1的整数,则:
=????×?????????????
=????×?????????????
=????×????+????×?????????
= ?????????×????×????+????
?
?????????????
?
上面的式子化成了几个整式乘积的形式.
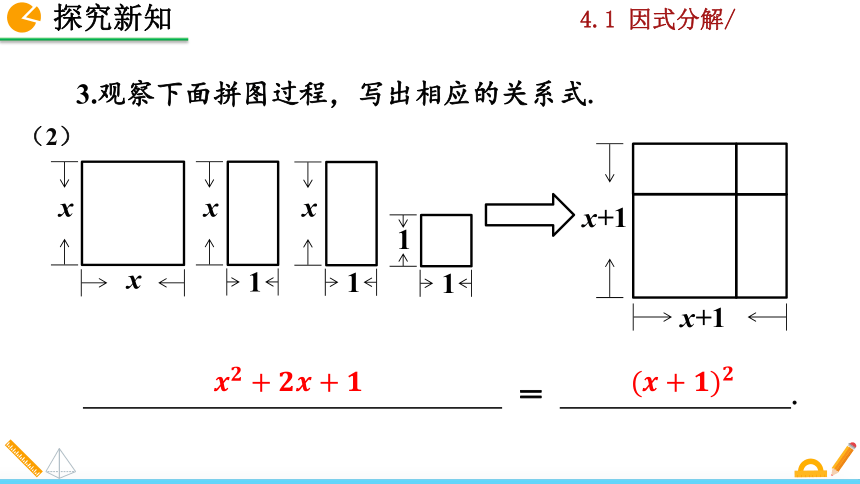
3.观察下面拼图过程,写出相应的关系式.
(1)
探究新知
m
m
m
m
a
b
c
a+b+c
= .
m(a+b+c)
?
am+bm+cm
?
3.观察下面拼图过程,写出相应的关系式.
(2)
探究新知
x
x
x+1
1
x+1
= .
x
x
1
1
1
(????+????)????
?
????????+????????+????
?
4.大家观察,这几个式子的变形有什么特点?
?????????????=????(????+????)(?????????),
????????+????????+????????=????(????+????+????),
????????+????????+????=(????+????)????.
?
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
①分解的对象必须是多项式;
②分解的结果一定是几个整式的乘积的形式,且每个因式的次数不能高于原来多项式的次数;
③必须分解到每个多项式都不能再分解为止.
结论
探究新知
注意:
例1????????????????????????????????????????能被45整除吗?
?
探究新知
解:??????????????????????????????????????
=(????????)?????(????????)?????(????????)????????
=??????????????????????????????????????
=????????????(??????????????????)
=?????????????????
=??????????????????????
=?????????????????????
?
∴ ??????????????????????????????????????能被45整除.
?
利用因式分解判断能否整除
素养考点 1
当n为整数时,
证明:(????????+????)?????(?????????????)????是8的倍数.
?
解:(????????+????)?????(?????????????)????
=(????????+????+?????????????)(????????+?????????????+????)
=?????????????
=????????
∴ (????????+????)?????(?????????????)????是8的倍数.
?
巩固练习
变式训练
A. ????????+????+????=????????+????????+????????
B. ????????+????????=????(????+????)
C. ????????+????????+????=????????+????+????
D. ????????+????=????(????+????????)
?
B
探究新知
下列各式从左到右的变形中,是分解因式的是( )
例2?
?
考查因式分解的概念
素养考点 2
判断下列等式从左到右的变形是否为因式分解?
(1)????+?????????????=?????????????
?
(2)????????????????????=?????????????????????????????????
?
(3)?????????????????????????=(????+????????????????)(?????????????????????)
?
(4) ????????????????=????????????????+????????????????
?
(5) ?????????????????=(????+????)(?????????????)
?
不是
不是
不是
不是
巩固练习
变式训练
不是
完成下列题目:
?????????????= .
????+?????????????= .
(????+????)????= .
?
探究新知
知识点 2
因式分解与整式乘法的关系
根据左面算式,解决下列问题:
?????????????????= (????????)(??????????????).
?????????????????= (????????????)(?????????????).
????????+????????+????= (????????????)????.
?
?????????????????
?
?????????????????
?
????????+????????+????
?
????
?
?????????
?
????+????
?
?????????
?
????+????
?
观察同一行中,左右两边的等式有什么区别和联系?
探究新知
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是整式乘法,右边一栏是因式分解,
他们的运算是相反的.
想一想:整式乘法与因式分解有什么关系?
????+?????????????
?
?????????????????
?
整式乘法
因式分解
是互逆的恒等变形,即
例 (1)若多项式????????+????????+????分解因式的结果为
(????+????)(?????????),则????+????的值为 .
(2)若????????+????+????=(????+????)????,则????= ,
????= .
?
探究新知
-3
14
?
12
?
因式分解与整式乘法的关系的应用
素养考点 3
已知2x2+4x-b的一个因式为x-1,则b=_____.
6
巩固练习
变式训练
解析:由题意知x-1是2x2+4x-b的一个因式,
即x=1时, 2x2+4x-b=0
将x=1代入上式,得2+4-b=0,解得b=6.
(2020?丹阳)下列各式从左到右的变形属于因式分解且分解正确的是( )
A. ????+?????????????=?????????????
B. ?????????+?????????????=?(?????????)????
C. ????????+????????+????=????????+????+????
D. ????????????+????????=(????????+????)(?????????)
?
连接中考
B
1. 下列等式中,从左到右的变形中是因式分解的是( )
A. ?????????????????????+????=(?????????????)????
B. ?????????????????+????=?????????????+????
C. ?????????????????=?????????????????????????
D. ????+????????=????+????+????????
?
A
课堂检测
基础巩固题
2. 如果多项式????????????????????+?????????????????????????????????????的一个因式是????????????????,那么另一个因式是( )
A. c?b+5ac B.c+b?5ac
C. 15ac D.15ac
?
B
课堂检测
基础巩固题
3. 若多项式????????+????????+????(????、????是常数)分解因式后,有一个因式是????+????,则?????????的值为 .
?
1
课堂检测
基础巩固题
4. 已知????,????,????是△ABC的三边,且?????????+????????????+??????????????????????????????+????=????,试判断△ABC的形状.
?
解:∵?????????+????????????+??????????????????????????????+????=????,
∴ ?????????+????????????+?????????????????????=????,
即 ?????????+????(?????????)????=????.
根据三角形三边关系可知?????????+????>????,∴ ?????????=????,
∴ ????=????,∴△ABC为等腰三角形.
?
课堂检测
基础巩固题
(1)求被墨水污染的一次式;
解:被墨水污染的一次式为
?????????????????+?????????????????+?????????????
=????????????+????????????????????????????????????????????????+????
=??????????????
?
1.下面是一个正确的因式分解,但是其中部分一次式被墨水污染看不清了:????????????+?????????????+????????????????????=(?????????)(????????+????).
?
课堂检测
能力提升题
(2)若被污染的一次式的值不小于2,求????的取值范围.
?
解:根据题意得:??????????????≥????,
解得:????≤?????,
即????的取值范围是????≤?????.
?
课堂检测
2.已知????,????,????是△ABC的三边,试判断(????????+?????????????????)?????????????????????????的正负性.
?
解:(????????+?????????????????)?????????????????????????
=(????????+?????????????????)?????(????????????)????
=????????+?????????????????+????????????????????+??????????????????????????????
=(????+????)?????????????(?????????)?????????????
=????+????+????????+??????????????????+??????????????????
?
课堂检测
∵ ????,????,????是△ABC的三边,
∴ ????+????+????>????,????+?????????>????,?????????+????>????,??????????????∴原式?
能力提升题
代数基本定理告诉我们,对于形如????????+?????????????????????+…+?????????????????+????????=????(其中????????,????????,…,????????为整数)这样的方程,如果有整数根的话,那么整数根必定是?????????的约数.
例如方程????????+?????????????????????????+????=????的整数根只可能为±????,±????,代入检验得????=????时等式成立,故????????+?????????????????????????+?????含有因式?????????,所以原方程可转化为:?????????????????+?????????????=????,进而可求得方程的所有解.
根据以上阅读材料,请你解方程????????+??????????????????????????=????
?
课堂检测
拓广探索题
解:取????=±????,±????代入方程,得到????=????适合方程,
则原方程可以分解为?????????????????+????????+????=????,
解得????=????或????=?????+????或????=??????????.
?
课堂检测
因式分解
定 义
与整式乘法运算的关系
把一个多项式化成几个整式的乘积的形式,叫做因式分解,也可称为分解因式.
课堂小结
因式分解
整式乘法
多项式化为整式乘积
因式分解与整式乘法是互逆的恒等变形.
整式乘积化为多项式
北师大版 八年级 数学 下册
1. 630可以被哪些整数整除?
导入新知
思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
解决这个问题,需要对630进行分解质因数
????????????=????×????????×????×????
?
(1)单项式×单项式:3a?4b= .
(2)单项式×多项式:am+n= .
(3)多项式×多项式:a+bm+n= .
?
2.整式乘法类型
导入新知
12ab
?
am+an
?
am+an+bm+bn
?
(1)平方差公式: (a+b)(a?b?) = .
(2)完全平方公式: (a±b)2= .
?
3.特殊的整式乘法公式
a2±2ab+b2
a2-b2
1. 理解掌握因式分解的意义,会判断一个变形是否为因式分解.
2. 理解因式分解与整式乘法之间的联系与区别.
素养目标
1.?????????????????????能被100整除吗?
?
探究新知
知识点 1
因式分解的定义
小明是这样做的:
??????????????????????????
=????????×?????????????????????×????
=?????????????????????????
=????????×????????????????
=????????×????????×????????????.
所以,?????????????????????能被100整除.
?
你知道每一步的依据吗?
??????????????????????????
=????????×?????????????????????×????
=?????????????????????????
=????????×????????????????
=????????×????????×????????????.
所以,?????????????????????能被100整除.
?
?????????????????????还能被哪些正整数整除?
?
还能被98,99整除
探究新知
在这里,解决问题的关键是把一个数式
化成了几个数的积的形式.
2.将99换成其他任意一个大于1的整数,上述结论仍然成立吗?
探究新知
用a表示任意一个大于1的整数,则:
=????×?????????????
=????×?????????????
=????×????+????×?????????
= ?????????×????×????+????
?
?????????????
?
上面的式子化成了几个整式乘积的形式.
3.观察下面拼图过程,写出相应的关系式.
(1)
探究新知
m
m
m
m
a
b
c
a+b+c
= .
m(a+b+c)
?
am+bm+cm
?
3.观察下面拼图过程,写出相应的关系式.
(2)
探究新知
x
x
x+1
1
x+1
= .
x
x
1
1
1
(????+????)????
?
????????+????????+????
?
4.大家观察,这几个式子的变形有什么特点?
?????????????=????(????+????)(?????????),
????????+????????+????????=????(????+????+????),
????????+????????+????=(????+????)????.
?
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
①分解的对象必须是多项式;
②分解的结果一定是几个整式的乘积的形式,且每个因式的次数不能高于原来多项式的次数;
③必须分解到每个多项式都不能再分解为止.
结论
探究新知
注意:
例1????????????????????????????????????????能被45整除吗?
?
探究新知
解:??????????????????????????????????????
=(????????)?????(????????)?????(????????)????????
=??????????????????????????????????????
=????????????(??????????????????)
=?????????????????
=??????????????????????
=?????????????????????
?
∴ ??????????????????????????????????????能被45整除.
?
利用因式分解判断能否整除
素养考点 1
当n为整数时,
证明:(????????+????)?????(?????????????)????是8的倍数.
?
解:(????????+????)?????(?????????????)????
=(????????+????+?????????????)(????????+?????????????+????)
=?????????????
=????????
∴ (????????+????)?????(?????????????)????是8的倍数.
?
巩固练习
变式训练
A. ????????+????+????=????????+????????+????????
B. ????????+????????=????(????+????)
C. ????????+????????+????=????????+????+????
D. ????????+????=????(????+????????)
?
B
探究新知
下列各式从左到右的变形中,是分解因式的是( )
例2?
?
考查因式分解的概念
素养考点 2
判断下列等式从左到右的变形是否为因式分解?
(1)????+?????????????=?????????????
?
(2)????????????????????=?????????????????????????????????
?
(3)?????????????????????????=(????+????????????????)(?????????????????????)
?
(4) ????????????????=????????????????+????????????????
?
(5) ?????????????????=(????+????)(?????????????)
?
不是
不是
不是
不是
巩固练习
变式训练
不是
完成下列题目:
?????????????= .
????+?????????????= .
(????+????)????= .
?
探究新知
知识点 2
因式分解与整式乘法的关系
根据左面算式,解决下列问题:
?????????????????= (????????)(??????????????).
?????????????????= (????????????)(?????????????).
????????+????????+????= (????????????)????.
?
?????????????????
?
?????????????????
?
????????+????????+????
?
????
?
?????????
?
????+????
?
?????????
?
????+????
?
观察同一行中,左右两边的等式有什么区别和联系?
探究新知
联系:左右两式是同一多项式的不同表现形式.
区别:左边一栏是整式乘法,右边一栏是因式分解,
他们的运算是相反的.
想一想:整式乘法与因式分解有什么关系?
????+?????????????
?
?????????????????
?
整式乘法
因式分解
是互逆的恒等变形,即
例 (1)若多项式????????+????????+????分解因式的结果为
(????+????)(?????????),则????+????的值为 .
(2)若????????+????+????=(????+????)????,则????= ,
????= .
?
探究新知
-3
14
?
12
?
因式分解与整式乘法的关系的应用
素养考点 3
已知2x2+4x-b的一个因式为x-1,则b=_____.
6
巩固练习
变式训练
解析:由题意知x-1是2x2+4x-b的一个因式,
即x=1时, 2x2+4x-b=0
将x=1代入上式,得2+4-b=0,解得b=6.
(2020?丹阳)下列各式从左到右的变形属于因式分解且分解正确的是( )
A. ????+?????????????=?????????????
B. ?????????+?????????????=?(?????????)????
C. ????????+????????+????=????????+????+????
D. ????????????+????????=(????????+????)(?????????)
?
连接中考
B
1. 下列等式中,从左到右的变形中是因式分解的是( )
A. ?????????????????????+????=(?????????????)????
B. ?????????????????+????=?????????????+????
C. ?????????????????=?????????????????????????
D. ????+????????=????+????+????????
?
A
课堂检测
基础巩固题
2. 如果多项式????????????????????+?????????????????????????????????????的一个因式是????????????????,那么另一个因式是( )
A. c?b+5ac B.c+b?5ac
C. 15ac D.15ac
?
B
课堂检测
基础巩固题
3. 若多项式????????+????????+????(????、????是常数)分解因式后,有一个因式是????+????,则?????????的值为 .
?
1
课堂检测
基础巩固题
4. 已知????,????,????是△ABC的三边,且?????????+????????????+??????????????????????????????+????=????,试判断△ABC的形状.
?
解:∵?????????+????????????+??????????????????????????????+????=????,
∴ ?????????+????????????+?????????????????????=????,
即 ?????????+????(?????????)????=????.
根据三角形三边关系可知?????????+????>????,∴ ?????????=????,
∴ ????=????,∴△ABC为等腰三角形.
?
课堂检测
基础巩固题
(1)求被墨水污染的一次式;
解:被墨水污染的一次式为
?????????????????+?????????????????+?????????????
=????????????+????????????????????????????????????????????????+????
=??????????????
?
1.下面是一个正确的因式分解,但是其中部分一次式被墨水污染看不清了:????????????+?????????????+????????????????????=(?????????)(????????+????).
?
课堂检测
能力提升题
(2)若被污染的一次式的值不小于2,求????的取值范围.
?
解:根据题意得:??????????????≥????,
解得:????≤?????,
即????的取值范围是????≤?????.
?
课堂检测
2.已知????,????,????是△ABC的三边,试判断(????????+?????????????????)?????????????????????????的正负性.
?
解:(????????+?????????????????)?????????????????????????
=(????????+?????????????????)?????(????????????)????
=????????+?????????????????+????????????????????+??????????????????????????????
=(????+????)?????????????(?????????)?????????????
=????+????+????????+??????????????????+??????????????????
?
课堂检测
∵ ????,????,????是△ABC的三边,
∴ ????+????+????>????,????+?????????>????,?????????+????>????,??????????????∴原式?
能力提升题
代数基本定理告诉我们,对于形如????????+?????????????????????+…+?????????????????+????????=????(其中????????,????????,…,????????为整数)这样的方程,如果有整数根的话,那么整数根必定是?????????的约数.
例如方程????????+?????????????????????????+????=????的整数根只可能为±????,±????,代入检验得????=????时等式成立,故????????+?????????????????????????+?????含有因式?????????,所以原方程可转化为:?????????????????+?????????????=????,进而可求得方程的所有解.
根据以上阅读材料,请你解方程????????+??????????????????????????=????
?
课堂检测
拓广探索题
解:取????=±????,±????代入方程,得到????=????适合方程,
则原方程可以分解为?????????????????+????????+????=????,
解得????=????或????=?????+????或????=??????????.
?
课堂检测
因式分解
定 义
与整式乘法运算的关系
把一个多项式化成几个整式的乘积的形式,叫做因式分解,也可称为分解因式.
课堂小结
因式分解
整式乘法
多项式化为整式乘积
因式分解与整式乘法是互逆的恒等变形.
整式乘积化为多项式
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
