北师大版八年级数学下册4.3 公式法课件(第1课时 26张)
文档属性
| 名称 | 北师大版八年级数学下册4.3 公式法课件(第1课时 26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 919.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览







文档简介
4.3 公式法
(第1课时)
北师大版 八年级 数学 下册
导入新知
a米
b米
b米
a米
(a-b)
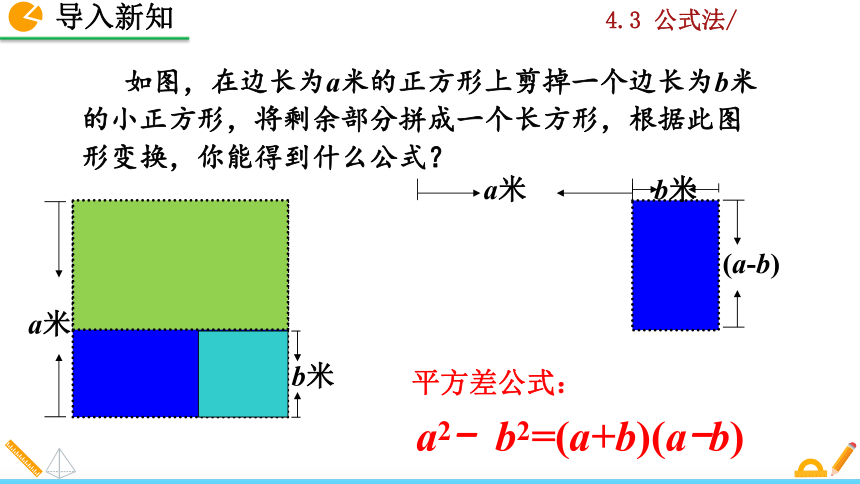
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
平方差公式:
1. 探索并运用平方差公式进行因式分解,体会逆向思维在数学中的作用.
2. 能综合运用提公因式法和平方差公式对多项式进行因式分解.
素养目标
探究新知
知识点 1
用平方差公式因式分解
计算下列各式:
????+?????????????= ;
????????+?????????????????= ;
????????+?????????????????????????= .
?
?????????????????
?
?????????????????????
?
?????????????????????????
?
思考:观察这些式子有什么共同特征?
结果都是二项式,其中每一项都是某数或式的平方,且两项符号相反(一正一负).
对下列各式进行因式分解:
探究新知
?????????????????= ;
?????????????????????= ;
?????????????????????????= .
?
????+?????????????
?
????????+?????????????????
?
????????+?????????????????????????
?
思考:观察这些式子有什么共同特征?
左边:是????,????两数的平方差的形式:
?
□-△
2
2
右边:是????,????两数之和与两数之差的积:
?
(□-△)(□+△)
探究新知
结论
文字语言:
两个数的平方差,等于这两个数的和与这两个数的差的积.这个公式就是平方差公式.
???????????=?(????+????)?(?????????)
?
平方差公式:
探究新知
?????????????????=?(????+????)(?????????)
?
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
形象地表示为:
①左边
②右边
相同项
相反项
探究新知
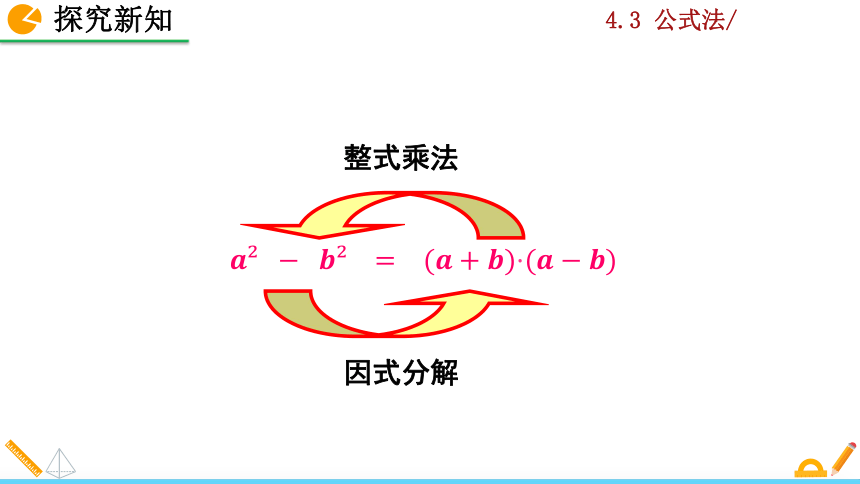
??????????????????=???(????+????)·(?????????)
?
整式乘法
因式分解
下列多项式可以用平方差公式因式分解吗?
(1)?????????????????????;
(2)????????????+????????;
(3)?????????????+????????;
(4)??????????????????????
?
√
×
√
×
注意:符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
探究新知
做一做:
探究新知
解:?(1)?????????????????????????=?????????(????????)????=(????+????????)(?????????????)
?
把下列各式因式分解:
例1
(1)?????????????????????????; (2)?????????????????????????????.
?
(2) ?????????????????????????????=(????????)?????(????????????)????=(????????+????????????)(?????????????????????)
?
????????????????=??(????+????)??(?????????)
?
用平方差公式因式分解
素养考点 1
把下列各式因式分解:
巩固练习
变式训练
解:?(1)?????????????????????????
=?????????????????????
=????????+?????????????????;
?
(1)?????????????????????????; (2)?????????????????+????????????????? .?
?
(2) ?????????????????+????????????????
=?????????????????????????????????
=?????????????????????????
=(????????+????????)(?????????????????) .
?
探究新知
素养考点 2
整体思想:整体用平方差公式
把下列各式因式分解:
例2
(1)????(????+????)?????(?????????)????
?
解:?(1)????(????+????)?????(?????????)????
=????(????+????)?????(?????????)????
=????????+????+(?????????)????????+?????(?????????)
=(????????+????????+?????????)(????????+?????????????+????)
=(????????+????????)(????????+????????)
=????(????????+????)(????+????????)
?
多项式
分解要彻底
探究新知
注意1:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
探究新知
(2)?????????????????????.
?
解:?(2)?????????????????????
=????????(?????????????)
=????????(?????????????????)
=????????(????+????)(?????????)
?
当多项式的各项含有公因式时,先提出公因式.
注意2:分解因式前应先分析多项式的特点,一般先提公因式,再套用公式.注意分解因式必须进行到每一个多项式都不能再分解因式为止.
分解因式:
巩固练习
变式训练
(1)??????????????????; (2)?????????????????????.
?
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
=ab(a+1)(a-1).
分解因式:
巩固练习
变式训练
(????????+????)?????(?????????????)????
?
解:(????????+????)?????(?????????????)????
=????????+????+?????????????????????+?????????+????????
=?????????????????+????????.
?
探究新知
素养考点 3
化简求值
例3 已知????????-????????=-????,????+????=????,求?????????,????,????的值.
?
∴????-????=-????②.
?
解:∵????????-????????=(????+????)(????-????)=-????,
?
????+????=????①,
?
联立①②组成二元一次方程组,
解得
????=-12
?
????=32
?
注意3:在与????????-????????,????±????有关的求代数式或未知数的值的问题中,通常需先因式分解,然后整体代入或联立方程组求值.
?
探究新知
巩固练习
变式训练
计算下列各题:
(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4 ×(53.52-46.52)
= 4 ×(53.5+46.5)(53.5-46.5)
=4×100×7=2800.
(2020?河北)若(?????????????)(?????????????????)????=????×????????×????????,
则????= .
?
连接中考
????????
?
解析:方程两边都乘以????,
得??????????????????????????????=????×????????×????????????,
∴????+?????????????????????+?????????????????=????×????????×????????????,
∴ ????????×????????????=????×????????×????????????,∴????=????????,
经检验, ????=????????是原方程的解,故????=????????.
?
1.下列多项式中能用平方差公式分解因式的是( )
A.????????+(?????)????? B.????????????-????????????????
C.-????????-???????? D.-????????+????
?
D
课堂检测
2.分解因式(????????+????)??????????2的结果是( )
A.3(????????+????????+????) B.????(????????+????????+????)
C.(????????+????)(????+????)??????????D.????(????+????)(????+????)?
?
D
基础巩固题
3.若????+????=????,?????????=????,则?????????????????的值为( )
?
A.-21 B.21 C.-10 D.10
A
4.若将(????????)?????????????分解成(????????????+????)(????????+????)(?????????????),则n的值是_____.
?
4
课堂检测
基础巩固题
5.如图,在边长为6.8 cm正方形钢板上,挖去4个边长为1.6 cm的小正方形,求剩余部分的面积.
解:根据题意,得
6.82-4×1.62
=6.82- (2×1.6)2
=6.82-3.22
=(6.8+3.2)(6.8 - 3.2)
=10×3.6
=36 (cm2)
答:剩余部分的面积为36 cm2.
课堂检测
基础巩固题
已知????????=????????+????, ????????=????????+????,????≠????,则
????????+????????????+????????的值为 .
?
16
解析:将????????=????????+????, ????????=????????+????相减,
得?????????????????=?????????????????,
∴????+?????????????=?????(?????????),
∴ ?????????????+????+????=????,
∵ ????≠????,∴ ????+????+????=????,即????+????=?????,
∴ ????????+????????????+????????=(????+????)????=????????.
?
课堂检测
能力提升题
一天,小明在纸上写了一个算式为4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”
课堂检测
解:
4x2+8x+11
=4(x2+2x)+11
=4(x2+2x+1-1)+11
=4(x+1)2-4+11
=4(x+1)2+7
∵4(x+1)2≥0,
即4x2+8x+11>0,所以小刚说得对.
∴4(x+1)2+7>0
拓广探索题
公 式 法
分 解 因 式
(平方差公式)
公 式
?????????????????=(????+????)(?????????)
?
课堂小结
一找 二套 三彻底
平方差公式因式分解的步骤
(第1课时)
北师大版 八年级 数学 下册
导入新知
a米
b米
b米
a米
(a-b)
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
平方差公式:
1. 探索并运用平方差公式进行因式分解,体会逆向思维在数学中的作用.
2. 能综合运用提公因式法和平方差公式对多项式进行因式分解.
素养目标
探究新知
知识点 1
用平方差公式因式分解
计算下列各式:
????+?????????????= ;
????????+?????????????????= ;
????????+?????????????????????????= .
?
?????????????????
?
?????????????????????
?
?????????????????????????
?
思考:观察这些式子有什么共同特征?
结果都是二项式,其中每一项都是某数或式的平方,且两项符号相反(一正一负).
对下列各式进行因式分解:
探究新知
?????????????????= ;
?????????????????????= ;
?????????????????????????= .
?
????+?????????????
?
????????+?????????????????
?
????????+?????????????????????????
?
思考:观察这些式子有什么共同特征?
左边:是????,????两数的平方差的形式:
?
□-△
2
2
右边:是????,????两数之和与两数之差的积:
?
(□-△)(□+△)
探究新知
结论
文字语言:
两个数的平方差,等于这两个数的和与这两个数的差的积.这个公式就是平方差公式.
???????????=?(????+????)?(?????????)
?
平方差公式:
探究新知
?????????????????=?(????+????)(?????????)
?
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
形象地表示为:
①左边
②右边
相同项
相反项
探究新知
??????????????????=???(????+????)·(?????????)
?
整式乘法
因式分解
下列多项式可以用平方差公式因式分解吗?
(1)?????????????????????;
(2)????????????+????????;
(3)?????????????+????????;
(4)??????????????????????
?
√
×
√
×
注意:符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
探究新知
做一做:
探究新知
解:?(1)?????????????????????????=?????????(????????)????=(????+????????)(?????????????)
?
把下列各式因式分解:
例1
(1)?????????????????????????; (2)?????????????????????????????.
?
(2) ?????????????????????????????=(????????)?????(????????????)????=(????????+????????????)(?????????????????????)
?
????????????????=??(????+????)??(?????????)
?
用平方差公式因式分解
素养考点 1
把下列各式因式分解:
巩固练习
变式训练
解:?(1)?????????????????????????
=?????????????????????
=????????+?????????????????;
?
(1)?????????????????????????; (2)?????????????????+????????????????? .?
?
(2) ?????????????????+????????????????
=?????????????????????????????????
=?????????????????????????
=(????????+????????)(?????????????????) .
?
探究新知
素养考点 2
整体思想:整体用平方差公式
把下列各式因式分解:
例2
(1)????(????+????)?????(?????????)????
?
解:?(1)????(????+????)?????(?????????)????
=????(????+????)?????(?????????)????
=????????+????+(?????????)????????+?????(?????????)
=(????????+????????+?????????)(????????+?????????????+????)
=(????????+????????)(????????+????????)
=????(????????+????)(????+????????)
?
多项式
分解要彻底
探究新知
注意1:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解.
探究新知
(2)?????????????????????.
?
解:?(2)?????????????????????
=????????(?????????????)
=????????(?????????????????)
=????????(????+????)(?????????)
?
当多项式的各项含有公因式时,先提出公因式.
注意2:分解因式前应先分析多项式的特点,一般先提公因式,再套用公式.注意分解因式必须进行到每一个多项式都不能再分解因式为止.
分解因式:
巩固练习
变式训练
(1)??????????????????; (2)?????????????????????.
?
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
=ab(a+1)(a-1).
分解因式:
巩固练习
变式训练
(????????+????)?????(?????????????)????
?
解:(????????+????)?????(?????????????)????
=????????+????+?????????????????????+?????????+????????
=?????????????????+????????.
?
探究新知
素养考点 3
化简求值
例3 已知????????-????????=-????,????+????=????,求?????????,????,????的值.
?
∴????-????=-????②.
?
解:∵????????-????????=(????+????)(????-????)=-????,
?
????+????=????①,
?
联立①②组成二元一次方程组,
解得
????=-12
?
????=32
?
注意3:在与????????-????????,????±????有关的求代数式或未知数的值的问题中,通常需先因式分解,然后整体代入或联立方程组求值.
?
探究新知
巩固练习
变式训练
计算下列各题:
(1)1012-992; (2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4 ×(53.52-46.52)
= 4 ×(53.5+46.5)(53.5-46.5)
=4×100×7=2800.
(2020?河北)若(?????????????)(?????????????????)????=????×????????×????????,
则????= .
?
连接中考
????????
?
解析:方程两边都乘以????,
得??????????????????????????????=????×????????×????????????,
∴????+?????????????????????+?????????????????=????×????????×????????????,
∴ ????????×????????????=????×????????×????????????,∴????=????????,
经检验, ????=????????是原方程的解,故????=????????.
?
1.下列多项式中能用平方差公式分解因式的是( )
A.????????+(?????)????? B.????????????-????????????????
C.-????????-???????? D.-????????+????
?
D
课堂检测
2.分解因式(????????+????)??????????2的结果是( )
A.3(????????+????????+????) B.????(????????+????????+????)
C.(????????+????)(????+????)??????????D.????(????+????)(????+????)?
?
D
基础巩固题
3.若????+????=????,?????????=????,则?????????????????的值为( )
?
A.-21 B.21 C.-10 D.10
A
4.若将(????????)?????????????分解成(????????????+????)(????????+????)(?????????????),则n的值是_____.
?
4
课堂检测
基础巩固题
5.如图,在边长为6.8 cm正方形钢板上,挖去4个边长为1.6 cm的小正方形,求剩余部分的面积.
解:根据题意,得
6.82-4×1.62
=6.82- (2×1.6)2
=6.82-3.22
=(6.8+3.2)(6.8 - 3.2)
=10×3.6
=36 (cm2)
答:剩余部分的面积为36 cm2.
课堂检测
基础巩固题
已知????????=????????+????, ????????=????????+????,????≠????,则
????????+????????????+????????的值为 .
?
16
解析:将????????=????????+????, ????????=????????+????相减,
得?????????????????=?????????????????,
∴????+?????????????=?????(?????????),
∴ ?????????????+????+????=????,
∵ ????≠????,∴ ????+????+????=????,即????+????=?????,
∴ ????????+????????????+????????=(????+????)????=????????.
?
课堂检测
能力提升题
一天,小明在纸上写了一个算式为4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”
课堂检测
解:
4x2+8x+11
=4(x2+2x)+11
=4(x2+2x+1-1)+11
=4(x+1)2-4+11
=4(x+1)2+7
∵4(x+1)2≥0,
即4x2+8x+11>0,所以小刚说得对.
∴4(x+1)2+7>0
拓广探索题
公 式 法
分 解 因 式
(平方差公式)
公 式
?????????????????=(????+????)(?????????)
?
课堂小结
一找 二套 三彻底
平方差公式因式分解的步骤
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
