北师大版八年级数学下册4.3 公式法课件(第2课时 29张)
文档属性
| 名称 | 北师大版八年级数学下册4.3 公式法课件(第2课时 29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 928.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览






文档简介
4.3 公式法
(第2课时)
北师大版 八年级 数学 下册
导入新知
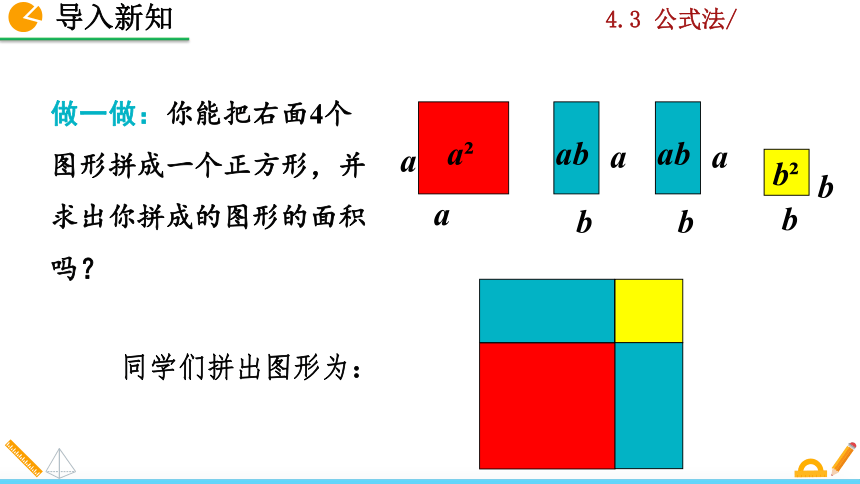
做一做:你能把右面4个图形拼成一个正方形,并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a?
b?
ab
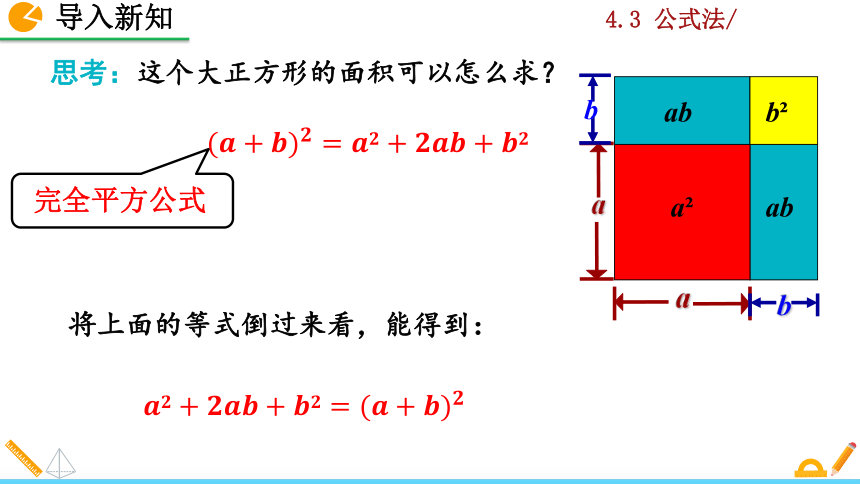
思考:这个大正方形的面积可以怎么求?
a
b
a
b
a?
ab
ab
b?
(????+????)????=????????+????????????+????????
?
将上面的等式倒过来看,能得到:
????????+????????????+????????=(????+????)????
?
完全平方公式
导入新知
1. 理解并掌握用完全平方公式分解因式.
2. 灵活应用各种方法分解因式,并能利用因式分解进行计算.
素养目标
判断下列各式从左到右的变形,是不是因式分解?
如果是,运用了哪种方法?
(1)(a?3)(a+3)=a2?9;
(2)x2+x=x(x+1);
(3)4x2?9=(2x+3)(2x?3);
(4)?x2+4x+4=(x+2)2.
?
探究新知
知识点 1
完全平方公式与完全平方式
不是,是整式乘法
是,运用提公因式法
是,运用平方差公式
是
完全平方公式
探究新知
整式乘法
因式分解
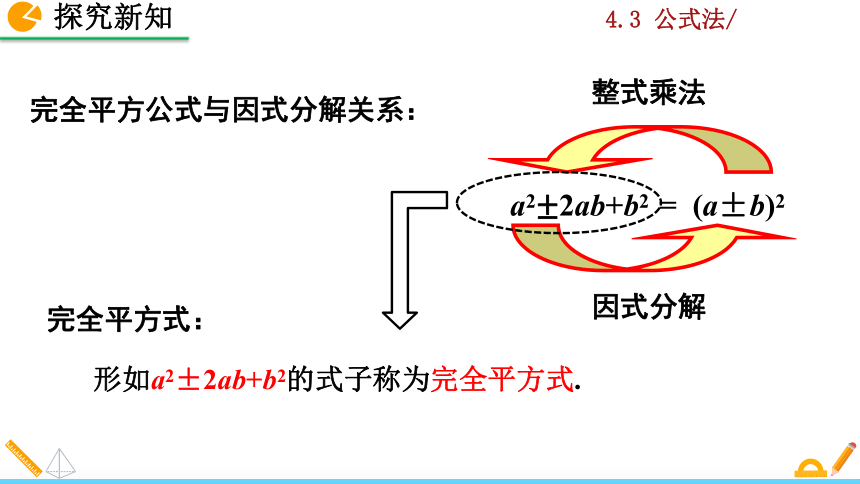
a2±2ab+b2??= (a±b)2
?
完全平方公式与因式分解关系:
形如a2±2ab+b2的式子称为完全平方式.
?
完全平方式:
探究新知
完全平方式的特点:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同.
是第一项和第三项底数的积的±2倍.
观察这两个式子:
a2+2ab+b2,a2?2ab+b2
?
结论
完全平方式的特点:
1. 三项式(或可以看成三项的);
2. 有两项为数或式的平方和;
3. 有一项为两数或式乘积的2倍,与符号无关.
探究新知
简记口诀:“首平方,尾平方,首尾两倍在中央”.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
探究新知
探究新知
完全平方式
素养考点 1
例 下列各式是不是完全平方式?
(1)????????-????????+????;
(2)????+?????????;
(3)????????????+?????????????;
(4)????????+????????+????????;
(5)????????+????+????.????????.
?
不是,它只有两项;
不是,?????????与?????的符号不统一;
?
不是,因为????????不是????与????的积的2倍;
?
是;
是.
巩固练习
变式训练
将前面例题的(2)(3)(4)变为完全平方式?
(2)????+?????????;
(3)????????????+?????????????;
(4)????????+????????+????????.
?
????+?????????+????????;
?
????????????+????????+????;
?
????????+????????????+????????.
?
探究新知
知识点 2
用完全平方公式因式分解
(3)a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
(2)m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
(1)x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
?
m
m - 3
3
x
2
m
3
以上等式即为利用完全平方公式得到的因式分解.
探究新知
素养考点 2
用完全平方公式因式分解
把下列完全平方式因式分解:
(1) ????????+????????????+????????; (2) ????+?????????????????+????+????.
?
例
解:?(1)????????+????????????+????????
=????????+??????????????+????????
=(????+????)????
?
?(2)????+?????????????????+????+????
=[????+?????????)]????
=(????+?????????)????
?
找到两个数或式是关键
分解因式:
(1)????????????????+????????????+????; (2)?????????+?????????????????????????.
?
巩固练习
变式训练
解: (1)????????????????+????????????+????
?
?=(????????+????)????;
?
=????????????+????·????????·????+(????)????
?
??(2)?????????+???????????????????????????
?
???=?(?????????????????????+????????????)
?
???=?(?????????????)????.
?
把下列完全平方公式分解因式:
(1)1002-2×100×99+99?;
(2)342+34×32+162.
巩固练习
变式训练
解:(1)原式=(100-99)?
(2)原式=(34+16)2
=1.
=2500.
探究新知
知识点 3
公式法
公式法分解因式
根据因式分解与整式乘法的关系,我们可以利用
乘法公式把某些多项式因式分解,这种因式分解的
方法叫做公式法.
完全平方公式
平方差公式
公式法
分解因式
提公因式法
一
先提公因式(有公因式)
二
平方差公式(剩余两项)
三
完全平方公式(剩余三项)
四
结果必须到不能分解为止
有一些可以用整体的思想看成两项或三项
因式分解的方法与步骤
探究新知
把下列各式因式分解:
(1)????????????????+????????????????+????????????????;(2)??????????????????????+????????????.
?
(1)????????????????+????????????????+????????????????
=????????????????+????????????+????????
=????????(????+????)????;
?
解:
(2)??????????????????????+????????????
=?????????+?????????????????????????
=????????????????????????????+????????????
=?(?????????????)????.
?
探究新知
素养考点 3
因式分解的综合运用
例1
因式分解:(1)-????????????????????+????????????????????-????????????????;
(2)(????????+????)????-????????????????.
?
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
巩固练习
变式训练
探究新知
例4 先分解因式,再计算求值:
已知?????????=????,????????=????,求?????????????????????????????????+????????????的值.
?
解: ?????????????????????????????????+????????????
=?????????????????????????????+????????
=????????(?????????)????
∵ ?????????=????,????????=????,
∴原式=2.
?
已知????????-????????+????????-????????????+????????=????,求????????????????+????????????+????的值.
?
=112=121.
解:∵x2-4x+y2-10y+29=0,
∴(????-????)????+(????-????)????=????.
?
∵(????-????)????≥????,(????-????)????≥????,
?
∴????-????=????,????-????=????,
?
∴????=????,????=????,
?
∴????????????????+????????????+????=(????????+????)????
?
变式训练
巩固练习
(2020?眉山)已知????????+????????????????=??????????????????,则?????????????????????的值为 .
?
连接中考
4
?
解析:由????????+????????????????=??????????????????,
得????????+?????????????????????????+????+????=????,
即?????????????????+????+????????????????+????+????=????,
∴(?????????)????+(????????????+????)????=????,可得????=????, ????=?????,
∴ ?????????????????????=????.
?
1.下列四个多项式中,能因式分解的是( )
A.????????+???? B.????????-????????+????
C.????????+???????? D.????????-????????
?
B
2.下列各式中,能用完全平方公式分解的是( )
A. ????????+????????+???????? B. ????????+?????????????????????
C. ?????????????????+???????????? D. ?????????????+????????+????????
?
D
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是( )
A . 11 B. 9 C. -11 D. -9
B
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
基础巩固题
5.利用因式分解计算????????????????????????+????????????+????= ________.
?
1100
?
课堂检测
基础巩固题
6.因式分解:
????(?????????)????+?????????????????????+????+????????+????????= .
?
5x?y????
?
因式分解:?????????????????????????????+?????????????????????.
?
解:分组分解法(方法不唯一):
?????????????????????????????+??????????????????????
=??????????????????????????????????????+????????????
=(?????????????????????????????)?(?????????????????????)
=????????(?????????????)?????(?????????????)
=(?????????????)(?????????????)
?
课堂检测
能力提升题
已知?????????=????,????????=?????????,
(1)求?????????????????????????的值;(2)求????????+????????的值;
?
解:(1) ∵?????????=????, ????????=?????????,
∴ ?????????????????????????=?????????????????=??????????????=?????????;
(2) ∵?????????=????, ????????=?????????,
∴ (?????????)????=????????,
∴ ?????????????????????+????????=????????, ∴ ????????+????????=????????;
?
课堂检测
拓广探索题
已知?????????=????,????????=?????????,
(3)求????+????的值.
?
解:(3) ∵????????+????????=????????,
∴(????+????)????=????????+????????????=?????????????????=????,
∴ ????+????=±????.
?
课堂检测
公 式 法
分 解 因 式
(完全平方公式)
公 式
a2±2ab+b2=(a±b)2
?
课堂小结
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
特 点
(第2课时)
北师大版 八年级 数学 下册
导入新知
做一做:你能把右面4个图形拼成一个正方形,并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a?
b?
ab
思考:这个大正方形的面积可以怎么求?
a
b
a
b
a?
ab
ab
b?
(????+????)????=????????+????????????+????????
?
将上面的等式倒过来看,能得到:
????????+????????????+????????=(????+????)????
?
完全平方公式
导入新知
1. 理解并掌握用完全平方公式分解因式.
2. 灵活应用各种方法分解因式,并能利用因式分解进行计算.
素养目标
判断下列各式从左到右的变形,是不是因式分解?
如果是,运用了哪种方法?
(1)(a?3)(a+3)=a2?9;
(2)x2+x=x(x+1);
(3)4x2?9=(2x+3)(2x?3);
(4)?x2+4x+4=(x+2)2.
?
探究新知
知识点 1
完全平方公式与完全平方式
不是,是整式乘法
是,运用提公因式法
是,运用平方差公式
是
完全平方公式
探究新知
整式乘法
因式分解
a2±2ab+b2??= (a±b)2
?
完全平方公式与因式分解关系:
形如a2±2ab+b2的式子称为完全平方式.
?
完全平方式:
探究新知
完全平方式的特点:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同.
是第一项和第三项底数的积的±2倍.
观察这两个式子:
a2+2ab+b2,a2?2ab+b2
?
结论
完全平方式的特点:
1. 三项式(或可以看成三项的);
2. 有两项为数或式的平方和;
3. 有一项为两数或式乘积的2倍,与符号无关.
探究新知
简记口诀:“首平方,尾平方,首尾两倍在中央”.
2
a
b
+b2
±
=(a ± b)?
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
探究新知
探究新知
完全平方式
素养考点 1
例 下列各式是不是完全平方式?
(1)????????-????????+????;
(2)????+?????????;
(3)????????????+?????????????;
(4)????????+????????+????????;
(5)????????+????+????.????????.
?
不是,它只有两项;
不是,?????????与?????的符号不统一;
?
不是,因为????????不是????与????的积的2倍;
?
是;
是.
巩固练习
变式训练
将前面例题的(2)(3)(4)变为完全平方式?
(2)????+?????????;
(3)????????????+?????????????;
(4)????????+????????+????????.
?
????+?????????+????????;
?
????????????+????????+????;
?
????????+????????????+????????.
?
探究新知
知识点 2
用完全平方公式因式分解
(3)a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
(2)m?-6m+9=( )? - 2· ( ) ·( )+( )? =( )?
(1)x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a?±2ab+b?=(a±b)?,填空:
?
m
m - 3
3
x
2
m
3
以上等式即为利用完全平方公式得到的因式分解.
探究新知
素养考点 2
用完全平方公式因式分解
把下列完全平方式因式分解:
(1) ????????+????????????+????????; (2) ????+?????????????????+????+????.
?
例
解:?(1)????????+????????????+????????
=????????+??????????????+????????
=(????+????)????
?
?(2)????+?????????????????+????+????
=[????+?????????)]????
=(????+?????????)????
?
找到两个数或式是关键
分解因式:
(1)????????????????+????????????+????; (2)?????????+?????????????????????????.
?
巩固练习
变式训练
解: (1)????????????????+????????????+????
?
?=(????????+????)????;
?
=????????????+????·????????·????+(????)????
?
??(2)?????????+???????????????????????????
?
???=?(?????????????????????+????????????)
?
???=?(?????????????)????.
?
把下列完全平方公式分解因式:
(1)1002-2×100×99+99?;
(2)342+34×32+162.
巩固练习
变式训练
解:(1)原式=(100-99)?
(2)原式=(34+16)2
=1.
=2500.
探究新知
知识点 3
公式法
公式法分解因式
根据因式分解与整式乘法的关系,我们可以利用
乘法公式把某些多项式因式分解,这种因式分解的
方法叫做公式法.
完全平方公式
平方差公式
公式法
分解因式
提公因式法
一
先提公因式(有公因式)
二
平方差公式(剩余两项)
三
完全平方公式(剩余三项)
四
结果必须到不能分解为止
有一些可以用整体的思想看成两项或三项
因式分解的方法与步骤
探究新知
把下列各式因式分解:
(1)????????????????+????????????????+????????????????;(2)??????????????????????+????????????.
?
(1)????????????????+????????????????+????????????????
=????????????????+????????????+????????
=????????(????+????)????;
?
解:
(2)??????????????????????+????????????
=?????????+?????????????????????????
=????????????????????????????+????????????
=?(?????????????)????.
?
探究新知
素养考点 3
因式分解的综合运用
例1
因式分解:(1)-????????????????????+????????????????????-????????????????;
(2)(????????+????)????-????????????????.
?
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
巩固练习
变式训练
探究新知
例4 先分解因式,再计算求值:
已知?????????=????,????????=????,求?????????????????????????????????+????????????的值.
?
解: ?????????????????????????????????+????????????
=?????????????????????????????+????????
=????????(?????????)????
∵ ?????????=????,????????=????,
∴原式=2.
?
已知????????-????????+????????-????????????+????????=????,求????????????????+????????????+????的值.
?
=112=121.
解:∵x2-4x+y2-10y+29=0,
∴(????-????)????+(????-????)????=????.
?
∵(????-????)????≥????,(????-????)????≥????,
?
∴????-????=????,????-????=????,
?
∴????=????,????=????,
?
∴????????????????+????????????+????=(????????+????)????
?
变式训练
巩固练习
(2020?眉山)已知????????+????????????????=??????????????????,则?????????????????????的值为 .
?
连接中考
4
?
解析:由????????+????????????????=??????????????????,
得????????+?????????????????????????+????+????=????,
即?????????????????+????+????????????????+????+????=????,
∴(?????????)????+(????????????+????)????=????,可得????=????, ????=?????,
∴ ?????????????????????=????.
?
1.下列四个多项式中,能因式分解的是( )
A.????????+???? B.????????-????????+????
C.????????+???????? D.????????-????????
?
B
2.下列各式中,能用完全平方公式分解的是( )
A. ????????+????????+???????? B. ????????+?????????????????????
C. ?????????????????+???????????? D. ?????????????+????????+????????
?
D
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是( )
A . 11 B. 9 C. -11 D. -9
B
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
基础巩固题
5.利用因式分解计算????????????????????????+????????????+????= ________.
?
1100
?
课堂检测
基础巩固题
6.因式分解:
????(?????????)????+?????????????????????+????+????????+????????= .
?
5x?y????
?
因式分解:?????????????????????????????+?????????????????????.
?
解:分组分解法(方法不唯一):
?????????????????????????????+??????????????????????
=??????????????????????????????????????+????????????
=(?????????????????????????????)?(?????????????????????)
=????????(?????????????)?????(?????????????)
=(?????????????)(?????????????)
?
课堂检测
能力提升题
已知?????????=????,????????=?????????,
(1)求?????????????????????????的值;(2)求????????+????????的值;
?
解:(1) ∵?????????=????, ????????=?????????,
∴ ?????????????????????????=?????????????????=??????????????=?????????;
(2) ∵?????????=????, ????????=?????????,
∴ (?????????)????=????????,
∴ ?????????????????????+????????=????????, ∴ ????????+????????=????????;
?
课堂检测
拓广探索题
已知?????????=????,????????=?????????,
(3)求????+????的值.
?
解:(3) ∵????????+????????=????????,
∴(????+????)????=????????+????????????=?????????????????=????,
∴ ????+????=±????.
?
课堂检测
公 式 法
分 解 因 式
(完全平方公式)
公 式
a2±2ab+b2=(a±b)2
?
课堂小结
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
特 点
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
