北师大版八年级数学下册5.1 认识分式课件(第1课时 37张)
文档属性
| 名称 | 北师大版八年级数学下册5.1 认识分式课件(第1课时 37张) |  | |
| 格式 | pptx | ||
| 文件大小 | 595.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:45:12 | ||
图片预览








文档简介
5.1 认识分式
(第1课时)
北师大版 八年级 数学 下册
(1)如果乐乐的速度是7米/秒,那么她所用的时间是( )秒;
(2)如果乐乐的速度是a米/秒,那么她所用的时间是( )秒;
(3)如果乐乐原来的速度是a米/秒,经过训练她的速度每秒增加了1米,那么她现在所用的时间是( )秒.
填空:乐乐同学参加百米赛跑
导入新知
(4)后勤老师若把体积为200 cm3的水倒入底面积为33 cm2的圆柱形保温桶中,水面高度为( )cm;若把体积为V 的水倒入底面积为S 的圆柱形容器中,水面高度为( ).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,合计为 元.
(8a+b)
导入新知
1. 了解分式的概念.
2. 理解分式有意义的条件及分式值为零的条件.
素养目标
3. 能熟练地求出分式有意义的条件及分式的值为零的条件.
做一做:请将上面问题中得到的式子分类:
单项式:
多项式:
既不是单项式也不是多项式:
8a+b.
8a+b
整
式
探究新知
知识点 1
分式的概念
它们有什么相同点和不同点?
相同点
不同点
(观察分母)
从形式上都具有分数 形式
分母中是否含有字母
(分子f、分母 g 都是整式)
想一想:式子
探究新知
分式的定义
一般地,用A,B表示两个整式,A÷B可以表示成 的形式, 且B中含有字母,那么称 为分式.其中A称为分式的分子,B称为分式的分母.对于任意一个分式,分母不能为零.
注意:
(1)分式也是代数式;
(2)分式是两个整式的商,它的形式是 (其中A,B都是
整式并且还要求B是含有字母的整式);
(3)A称为分式的分子,B为分式的分母.
结论
探究新知
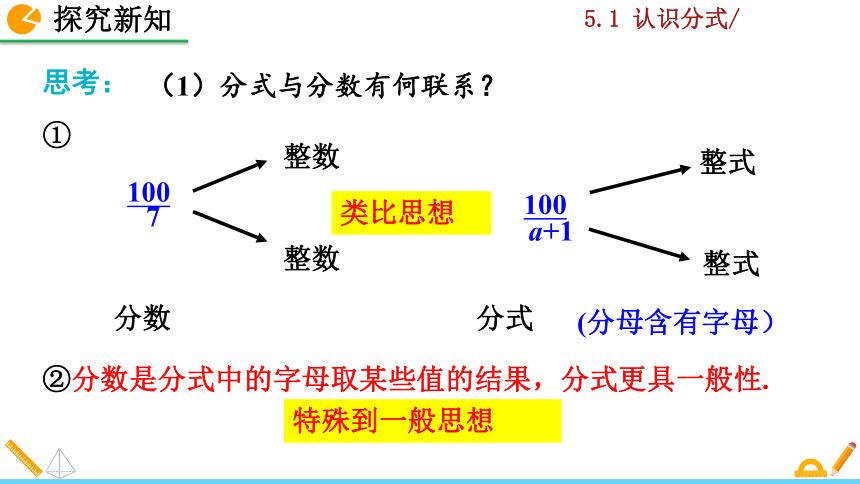
(1)分式与分数有何联系?
②分数是分式中的字母取某些值的结果,分式更具一般性.
整数
整数
整式
整式
(分母含有字母)
分数
分式
类比思想
特殊到一般思想
①
7
100
a+1
100
思考:
探究新知
整数
分数
整式
分式
有理数
有理式
数、式通性
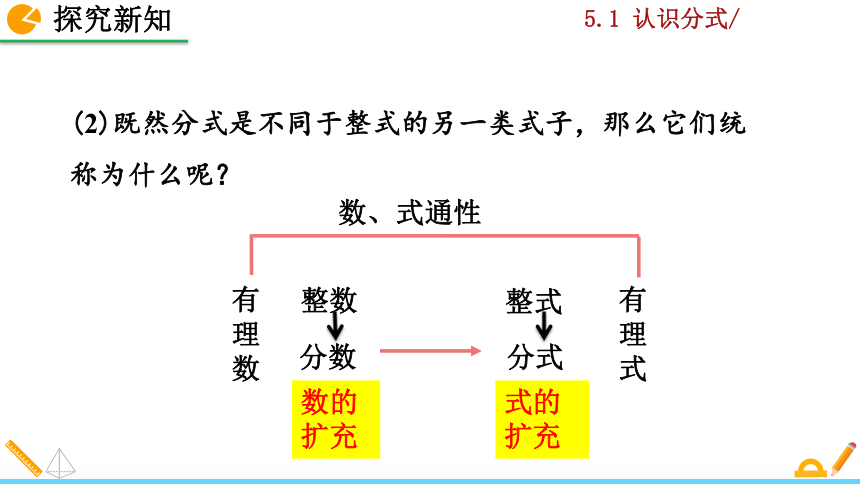
(2)既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数的扩充
式的扩充
探究新知
单项式
多项式
代数式
有理式
整式
分式
无理式
有理数
整数
分数
实数
无理数
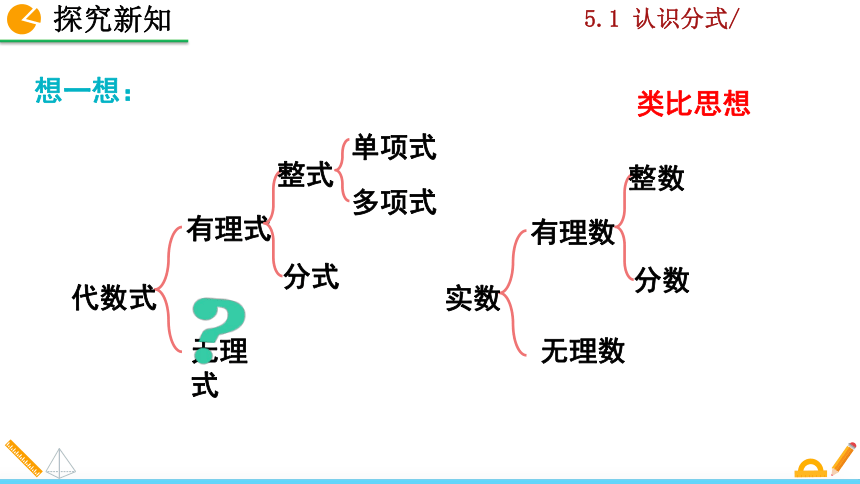
类比思想
想一想:
探究新知
下面的式子哪些是分式?
分式:
判一判:
探究新知
方法总结
1.判断时,注意含有 的式子, 是常数.
2.式子中含有多项时,若其中有一项分
母含有字母,则该式也为分式,如:
.
探究新知
下列各式中,分式有( )
A.2个 B.3个 C.4个 D.5个
B
分式的概念
素养考点 1
探究新知
例
提示:
辨别分式的“两个关键”
探究新知
看形式——是否为 的形式(A、B为整式)
看分母——分母B中必须含有字母
下列各式:
其中分式共有 ( )
A.2个 B.3个 C.4个 D.5个
B
巩固练习
变式训练
想一想:我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式 中的分母应满足什么条件?
当B=0时,分式 无意义.
当B≠0时,分式 有意义.
探究新知
知识点 2
分式有意义的条件
思考:已知分式 ,
(1) 当 x=3 时,分式的值是多少?
(2) 当x=-2时,你能算出来吗?
不行,当x=-2时,分式分母为0,没有意义.
即当x______时,分式有意义.
(3)当x为何值时,分式有意义?
当 x=3 时,分式值为
一般到特殊思想
类比思想
≠-2
探究新知
若代数式 有意义,则实数x的取值范围是 ( )
A. x=-1 B. x=3 C. x≠-1 D. x≠3
D
分式有无意义的条件
素养考点 2
探究新知
例1
方法总结
分式有、无意义的条件的注意事项
1.分式有意义?分母不为零,
分式无意义?分母为零.
2.在确定分式有无意义时,不能对分式进行约分,否则会扩大字母的取值范围.
探究新知
(1)当a=1,2,-1时,分别求出分式 的值;
(2)当a取何值时,分式有意义?
解:(1)当a=1时,
当a=2时,
当a=-1时,
(2)当分母的值等于零时,分式没有意义,除此之外,分式都有意义.
由分母2a-1=0,得
所以,当 时,分式 有意义.
例2
探究新知
已知分式 有意义,则x应满足的
条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠2 D.以上结果都不对
方法总结:分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
C
巩固练习
变式训练
想一想:分式 的值为零应满足什么条件?
当f=0而 g≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
探究新知
知识点 3
分式值为零的条件
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x = 1时,分式
∴ x ≠ -1.
而 x+1≠0,
∴x = ±1,
则 x2 - 1=0,
例 当x为何值时,分式 的值为零?
分式值为零的条件
素养考点 3
探究新知
方法总结
分式值为零的求法
(1)利用分子等于0,构建方程.
(2)解方程,求出所含字母的值.
(3)代入验证:将所求的值代入分母,验证是否使分母为0,不为0此值即为所求,否则,应舍去.
(4)写出答案.
探究新知
下列判断错误的是 ( )
A.当a≠0时,分式 有意义
B.当a=2时,分式 的值为0
C.当a>2时,分式 的值为正
D.当a=-2时,分式 的值为0
D
巩固练习
变式训练
连接中考
(2020·衡阳)要使分式 有意义,则x的取值范围是 ( )
A. x>1 B. x≠1 C. x=1 D. x≠0
B
1.下列各式中,哪些是整式?哪些是分式?
(1)5x-7; (2) (3)3x2-1;
(4) (5) (6)
(7) (8)
解:整式:(1)(2)(3)(8);
分式:(4)(5)(6)(7).
课堂检测
基础巩固题
2.求下列条件下分式 的值.
(1)x = 3; (2)x=-0.4.
解:(1)当 x = 3 时,
(2)当x = -0.4时,
课堂检测
基础巩固题
3.下列分式中,无论x取何值,分式总有意义的是 ( )
B
课堂检测
基础巩固题
解:∵式子 无意义,∴3y-1=0,
解得y=
原式=y2-x2+x2=y2=
4.若式子 无意义,求代数式(y+x)(y-x)+x2的值.
课堂检测
基础巩固题
分式 的值为 .
因此当 时,
(2)当 x -2=0,
即 x=2 时,
解: (1)当2x-3=0,即 时,
分式的值不存在;
5.当x取什么值时,分式 的值.
(1)不存在;(2)等于0?
有2x-3=1 ≠0,
课堂检测
基础巩固题
1.(1)当 时,分式 的值为零.
x=2
(2)若 的值为零,则x= .
-3
课堂检测
能力提升题
2.若分式 的值为正整数,则整数a的值有( )
A.3个 B.4个 C.6个 D.8个
B
课堂检测
能力提升题
现给一列分式: … (其中x,y均不为0).
(1)写出这列分式的第7个分式、第10个分式、第16个
分式以及第27个分式.
(2)求出这列分式的第2 019个分式除以第2 018个分式所得的商.并回答把任意一个分式除以前面的一个分式,你发现什么规律?用语言表示出来.
课堂检测
拓广探索题
解:(1)分子中x的次数是分式的序次的2倍加1,分母中y
的次数与序次一致,分式的序次为奇数时,分式的符号
为正,分式的序次为偶数时,分式的符号为负,于是第n
个分式为:(-1)n+1 这列分式中的第7个分式为:
第10个分式为:- 第16个分式为: 第27个分式为:
课堂检测
拓广探索题
(2)第2 019个分式除以第2 018个分式所得的商为:
规律是任意一个分式除以前面一个分式恒等于-
课堂检测
拓广探索题
分式
定义
值为零的条件
有意义的条件
分式 有意义的条件是 g ≠0.
分式 值为零的条件是 f=0且g ≠0.
一个整式 f 除以一个非零整式g(g中含字母)所得的商 .
课堂小结
(第1课时)
北师大版 八年级 数学 下册
(1)如果乐乐的速度是7米/秒,那么她所用的时间是( )秒;
(2)如果乐乐的速度是a米/秒,那么她所用的时间是( )秒;
(3)如果乐乐原来的速度是a米/秒,经过训练她的速度每秒增加了1米,那么她现在所用的时间是( )秒.
填空:乐乐同学参加百米赛跑
导入新知
(4)后勤老师若把体积为200 cm3的水倒入底面积为33 cm2的圆柱形保温桶中,水面高度为( )cm;若把体积为V 的水倒入底面积为S 的圆柱形容器中,水面高度为( ).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,合计为 元.
(8a+b)
导入新知
1. 了解分式的概念.
2. 理解分式有意义的条件及分式值为零的条件.
素养目标
3. 能熟练地求出分式有意义的条件及分式的值为零的条件.
做一做:请将上面问题中得到的式子分类:
单项式:
多项式:
既不是单项式也不是多项式:
8a+b.
8a+b
整
式
探究新知
知识点 1
分式的概念
它们有什么相同点和不同点?
相同点
不同点
(观察分母)
从形式上都具有分数 形式
分母中是否含有字母
(分子f、分母 g 都是整式)
想一想:式子
探究新知
分式的定义
一般地,用A,B表示两个整式,A÷B可以表示成 的形式, 且B中含有字母,那么称 为分式.其中A称为分式的分子,B称为分式的分母.对于任意一个分式,分母不能为零.
注意:
(1)分式也是代数式;
(2)分式是两个整式的商,它的形式是 (其中A,B都是
整式并且还要求B是含有字母的整式);
(3)A称为分式的分子,B为分式的分母.
结论
探究新知
(1)分式与分数有何联系?
②分数是分式中的字母取某些值的结果,分式更具一般性.
整数
整数
整式
整式
(分母含有字母)
分数
分式
类比思想
特殊到一般思想
①
7
100
a+1
100
思考:
探究新知
整数
分数
整式
分式
有理数
有理式
数、式通性
(2)既然分式是不同于整式的另一类式子,那么它们统称为什么呢?
数的扩充
式的扩充
探究新知
单项式
多项式
代数式
有理式
整式
分式
无理式
有理数
整数
分数
实数
无理数
类比思想
想一想:
探究新知
下面的式子哪些是分式?
分式:
判一判:
探究新知
方法总结
1.判断时,注意含有 的式子, 是常数.
2.式子中含有多项时,若其中有一项分
母含有字母,则该式也为分式,如:
.
探究新知
下列各式中,分式有( )
A.2个 B.3个 C.4个 D.5个
B
分式的概念
素养考点 1
探究新知
例
提示:
辨别分式的“两个关键”
探究新知
看形式——是否为 的形式(A、B为整式)
看分母——分母B中必须含有字母
下列各式:
其中分式共有 ( )
A.2个 B.3个 C.4个 D.5个
B
巩固练习
变式训练
想一想:我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式 中的分母应满足什么条件?
当B=0时,分式 无意义.
当B≠0时,分式 有意义.
探究新知
知识点 2
分式有意义的条件
思考:已知分式 ,
(1) 当 x=3 时,分式的值是多少?
(2) 当x=-2时,你能算出来吗?
不行,当x=-2时,分式分母为0,没有意义.
即当x______时,分式有意义.
(3)当x为何值时,分式有意义?
当 x=3 时,分式值为
一般到特殊思想
类比思想
≠-2
探究新知
若代数式 有意义,则实数x的取值范围是 ( )
A. x=-1 B. x=3 C. x≠-1 D. x≠3
D
分式有无意义的条件
素养考点 2
探究新知
例1
方法总结
分式有、无意义的条件的注意事项
1.分式有意义?分母不为零,
分式无意义?分母为零.
2.在确定分式有无意义时,不能对分式进行约分,否则会扩大字母的取值范围.
探究新知
(1)当a=1,2,-1时,分别求出分式 的值;
(2)当a取何值时,分式有意义?
解:(1)当a=1时,
当a=2时,
当a=-1时,
(2)当分母的值等于零时,分式没有意义,除此之外,分式都有意义.
由分母2a-1=0,得
所以,当 时,分式 有意义.
例2
探究新知
已知分式 有意义,则x应满足的
条件是 ( )
A.x≠1 B.x≠2
C.x≠1且x≠2 D.以上结果都不对
方法总结:分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
C
巩固练习
变式训练
想一想:分式 的值为零应满足什么条件?
当f=0而 g≠0时,分式 的值为零.
注意:分式值为零是分式有意义的一种特殊情况.
探究新知
知识点 3
分式值为零的条件
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x = 1时,分式
∴ x ≠ -1.
而 x+1≠0,
∴x = ±1,
则 x2 - 1=0,
例 当x为何值时,分式 的值为零?
分式值为零的条件
素养考点 3
探究新知
方法总结
分式值为零的求法
(1)利用分子等于0,构建方程.
(2)解方程,求出所含字母的值.
(3)代入验证:将所求的值代入分母,验证是否使分母为0,不为0此值即为所求,否则,应舍去.
(4)写出答案.
探究新知
下列判断错误的是 ( )
A.当a≠0时,分式 有意义
B.当a=2时,分式 的值为0
C.当a>2时,分式 的值为正
D.当a=-2时,分式 的值为0
D
巩固练习
变式训练
连接中考
(2020·衡阳)要使分式 有意义,则x的取值范围是 ( )
A. x>1 B. x≠1 C. x=1 D. x≠0
B
1.下列各式中,哪些是整式?哪些是分式?
(1)5x-7; (2) (3)3x2-1;
(4) (5) (6)
(7) (8)
解:整式:(1)(2)(3)(8);
分式:(4)(5)(6)(7).
课堂检测
基础巩固题
2.求下列条件下分式 的值.
(1)x = 3; (2)x=-0.4.
解:(1)当 x = 3 时,
(2)当x = -0.4时,
课堂检测
基础巩固题
3.下列分式中,无论x取何值,分式总有意义的是 ( )
B
课堂检测
基础巩固题
解:∵式子 无意义,∴3y-1=0,
解得y=
原式=y2-x2+x2=y2=
4.若式子 无意义,求代数式(y+x)(y-x)+x2的值.
课堂检测
基础巩固题
分式 的值为 .
因此当 时,
(2)当 x -2=0,
即 x=2 时,
解: (1)当2x-3=0,即 时,
分式的值不存在;
5.当x取什么值时,分式 的值.
(1)不存在;(2)等于0?
有2x-3=1 ≠0,
课堂检测
基础巩固题
1.(1)当 时,分式 的值为零.
x=2
(2)若 的值为零,则x= .
-3
课堂检测
能力提升题
2.若分式 的值为正整数,则整数a的值有( )
A.3个 B.4个 C.6个 D.8个
B
课堂检测
能力提升题
现给一列分式: … (其中x,y均不为0).
(1)写出这列分式的第7个分式、第10个分式、第16个
分式以及第27个分式.
(2)求出这列分式的第2 019个分式除以第2 018个分式所得的商.并回答把任意一个分式除以前面的一个分式,你发现什么规律?用语言表示出来.
课堂检测
拓广探索题
解:(1)分子中x的次数是分式的序次的2倍加1,分母中y
的次数与序次一致,分式的序次为奇数时,分式的符号
为正,分式的序次为偶数时,分式的符号为负,于是第n
个分式为:(-1)n+1 这列分式中的第7个分式为:
第10个分式为:- 第16个分式为: 第27个分式为:
课堂检测
拓广探索题
(2)第2 019个分式除以第2 018个分式所得的商为:
规律是任意一个分式除以前面一个分式恒等于-
课堂检测
拓广探索题
分式
定义
值为零的条件
有意义的条件
分式 有意义的条件是 g ≠0.
分式 值为零的条件是 f=0且g ≠0.
一个整式 f 除以一个非零整式g(g中含字母)所得的商 .
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
