北师大版八年级数学下册5.3 分式的加减法课件(第3课时 36张)
文档属性
| 名称 | 北师大版八年级数学下册5.3 分式的加减法课件(第3课时 36张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览








文档简介
5.3 分式的加减法
(第3课时)
北师大版 八年级 数学 下册
1.分式的乘除法法则是什么,用字母表示出来?
2.分式的加减法法则是什么,用字母表示出来?
导入新知
1.能够熟练计算较复杂的异分母分式的加减运算,复习并巩固分式的运算法则.
2.知道分式混合运算的运算顺序,能熟练地进行分式的混合运算.
素养目标
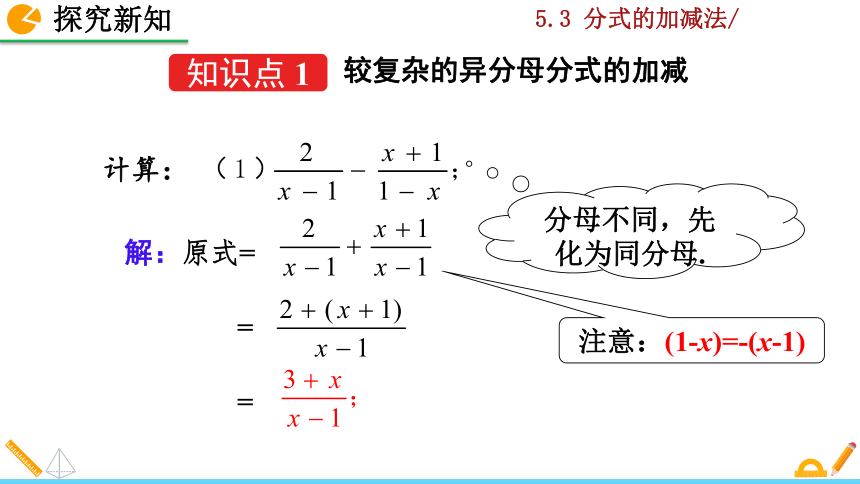
解:原式=
=
=
注意:(1-x)=-(x-1)
计算:
分母不同,先化为同分母.
探究新知
知识点 1
较复杂的异分母分式的加减
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
探究新知
解:原式=
=
=
注意:分母是多项式先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
探究新知
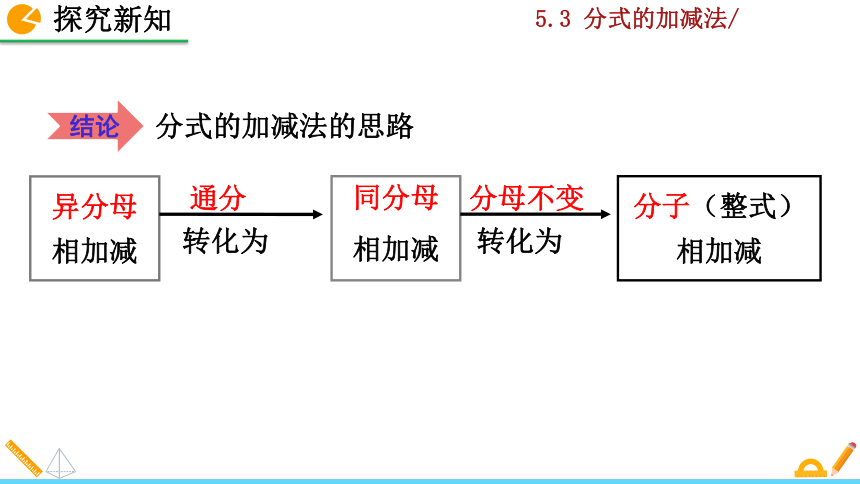
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
结论
探究新知
计算:
法一:
原式=
法二:
原式=
把整式看成分母为“1”的分式
探究新知
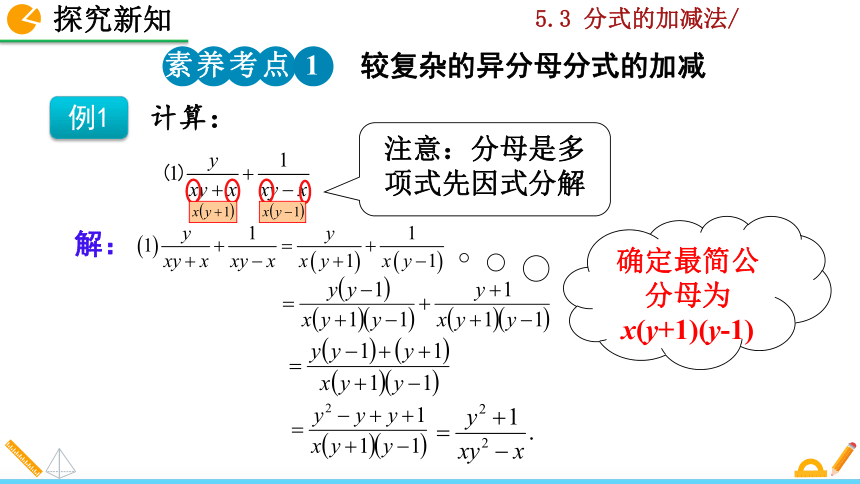
注意:分母是多项式先因式分解
确定最简公分母为x(y+1)(y-1)
例1
计算:
解:
探究新知
较复杂的异分母分式的加减
素养考点 1
把整式看成分母为“1”的式子
(2)解法1:
解法2:
探究新知
(2)
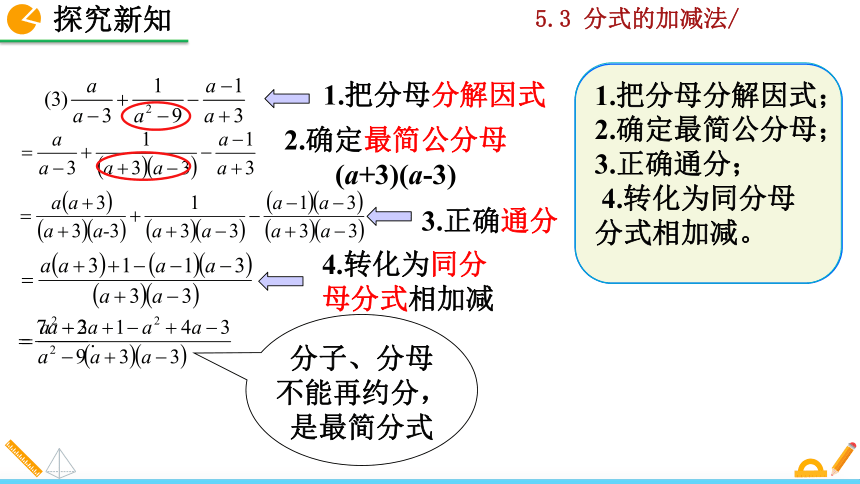
1.把分母分解因式
分子、分母不能再约分,是最简分式
1.把分母分解因式;
2.确定最简公分母;
3.正确通分;
4.转化为同分母分式相加减。
2.确定最简公分母(a+3)(a-3)
3.正确通分
4.转化为同分母分式相加减
探究新知
阅读下面题目的计算过程.
=
=
=
(1)上述计算过程,从哪一步开始错误,请写出该步的代号_______;
(2)错误原因___________;
(3)本题的正确结果为: .
②
漏掉了分母
①
②
③
④
巩固练习
变式训练
已知
,求
的值.
因为
即
所以,原式
1.把分母分解因式;
2.确定最简公分母;
3.正确通分;
4.转化为同分母分式相加减.
解:
例2
探究新知
先化简,再求值: ,其中
巩固练习
变式训练
解:
因为
所以原式
根据规划设计,某工程队准备修建一条长1120 m 的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期.假设原计划每天修建盲道x m,那么
(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
解:(1)原计划修建需 天,实际修建用了 天.
探究新知
(2)实际比原计划缩短的天数
异分母分式加减的实际应用
素养考点 2
蓄水池总量:ap t.
同时开放所需时间:
提前时间:
巩固练习
变式训练
解:
某蓄水池装有A、B两个进水管,每小时可分别进水a t,b t.若单独开放A进水管,p h可将该水池注满.如果A、B两根水管同时开放,那么能提前多长时间将该蓄水池注满?
思考:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
分式的混合运算
探究新知
知识点 2
解:
先乘方,再乘除,最后加减
探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
结论
探究新知
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,最后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
注意:
探究新知
解:
分式混合运算
素养考点 3
探究新知
例
计算:
方法总结
分式混合运算应注意的四个方面
(1)有理数的运算律对于分式同样适用.
(2)注意运算顺序,结果一定要化为最简分式或整式.
(3)分子或分母的系数是负数时,要把“-”提到分式的前面.
(4)当分式的分子、分母是多项式时,可先将分子、分母因式分解,再运算.
探究新知
计算:
(1)
(2)
巩固练习
变式训练
解:(1)原式=
巩固练习
(2)原式
连接中考
(2020·黄冈)计算: 的结果是 .
1.化简 的结果为( )
B
课堂检测
基础巩固题
2.先化简 ·(x2-1),再选取一个你喜欢的数代入求值.
原式= ·(x2-1)+ ·(x2-1)
=x-1+x+1=2x,
∵x+1≠0,x-1≠0,∴x≠±1,
∴可取x=2,原式=2x=4.
解:
课堂检测
基础巩固题
3.用两种方法计算:
解:(按运算顺序)
原式
课堂检测
基础巩固题
解: (利用乘法分配律)
原式
课堂检测
解:原式
4.计算:
课堂检测
基础巩固题
.
5.先化简,再求值: 其中a=
解:
课堂检测
当 时,原式=-4.
基础巩固题
1.计算:
分析:把 和 看成整体,题目的实
质是平方差公式的应用.
解:原式
课堂检测
能力提升题
2.若 ,求A,B的值.
解:
∴
解得
分析:先将等式两边化成同分母分式,然后对照两边的分子,可得到关于A,B的方程组.
课堂检测
能力提升题
∵
繁分式的化简:
解法1:原式
课堂检测
拓广探索题
解法2:
课堂检测
2.分式的混合运算法则
先算乘除,再算加减;如果有括号先算括号内的.
1.分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母相加减
分子(整式)相加减
分母不变
转化为
课堂小结
(第3课时)
北师大版 八年级 数学 下册
1.分式的乘除法法则是什么,用字母表示出来?
2.分式的加减法法则是什么,用字母表示出来?
导入新知
1.能够熟练计算较复杂的异分母分式的加减运算,复习并巩固分式的运算法则.
2.知道分式混合运算的运算顺序,能熟练地进行分式的混合运算.
素养目标
解:原式=
=
=
注意:(1-x)=-(x-1)
计算:
分母不同,先化为同分母.
探究新知
知识点 1
较复杂的异分母分式的加减
解:原式=
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
探究新知
解:原式=
=
=
注意:分母是多项式先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
探究新知
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
结论
探究新知
计算:
法一:
原式=
法二:
原式=
把整式看成分母为“1”的分式
探究新知
注意:分母是多项式先因式分解
确定最简公分母为x(y+1)(y-1)
例1
计算:
解:
探究新知
较复杂的异分母分式的加减
素养考点 1
把整式看成分母为“1”的式子
(2)解法1:
解法2:
探究新知
(2)
1.把分母分解因式
分子、分母不能再约分,是最简分式
1.把分母分解因式;
2.确定最简公分母;
3.正确通分;
4.转化为同分母分式相加减。
2.确定最简公分母(a+3)(a-3)
3.正确通分
4.转化为同分母分式相加减
探究新知
阅读下面题目的计算过程.
=
=
=
(1)上述计算过程,从哪一步开始错误,请写出该步的代号_______;
(2)错误原因___________;
(3)本题的正确结果为: .
②
漏掉了分母
①
②
③
④
巩固练习
变式训练
已知
,求
的值.
因为
即
所以,原式
1.把分母分解因式;
2.确定最简公分母;
3.正确通分;
4.转化为同分母分式相加减.
解:
例2
探究新知
先化简,再求值: ,其中
巩固练习
变式训练
解:
因为
所以原式
根据规划设计,某工程队准备修建一条长1120 m 的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期.假设原计划每天修建盲道x m,那么
(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
解:(1)原计划修建需 天,实际修建用了 天.
探究新知
(2)实际比原计划缩短的天数
异分母分式加减的实际应用
素养考点 2
蓄水池总量:ap t.
同时开放所需时间:
提前时间:
巩固练习
变式训练
解:
某蓄水池装有A、B两个进水管,每小时可分别进水a t,b t.若单独开放A进水管,p h可将该水池注满.如果A、B两根水管同时开放,那么能提前多长时间将该蓄水池注满?
思考:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
分式的混合运算
探究新知
知识点 2
解:
先乘方,再乘除,最后加减
探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
结论
探究新知
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,最后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
注意:
探究新知
解:
分式混合运算
素养考点 3
探究新知
例
计算:
方法总结
分式混合运算应注意的四个方面
(1)有理数的运算律对于分式同样适用.
(2)注意运算顺序,结果一定要化为最简分式或整式.
(3)分子或分母的系数是负数时,要把“-”提到分式的前面.
(4)当分式的分子、分母是多项式时,可先将分子、分母因式分解,再运算.
探究新知
计算:
(1)
(2)
巩固练习
变式训练
解:(1)原式=
巩固练习
(2)原式
连接中考
(2020·黄冈)计算: 的结果是 .
1.化简 的结果为( )
B
课堂检测
基础巩固题
2.先化简 ·(x2-1),再选取一个你喜欢的数代入求值.
原式= ·(x2-1)+ ·(x2-1)
=x-1+x+1=2x,
∵x+1≠0,x-1≠0,∴x≠±1,
∴可取x=2,原式=2x=4.
解:
课堂检测
基础巩固题
3.用两种方法计算:
解:(按运算顺序)
原式
课堂检测
基础巩固题
解: (利用乘法分配律)
原式
课堂检测
解:原式
4.计算:
课堂检测
基础巩固题
.
5.先化简,再求值: 其中a=
解:
课堂检测
当 时,原式=-4.
基础巩固题
1.计算:
分析:把 和 看成整体,题目的实
质是平方差公式的应用.
解:原式
课堂检测
能力提升题
2.若 ,求A,B的值.
解:
∴
解得
分析:先将等式两边化成同分母分式,然后对照两边的分子,可得到关于A,B的方程组.
课堂检测
能力提升题
∵
繁分式的化简:
解法1:原式
课堂检测
拓广探索题
解法2:
课堂检测
2.分式的混合运算法则
先算乘除,再算加减;如果有括号先算括号内的.
1.分式加减运算的方法思路:
通分
转化为
异分母相加减
同分母相加减
分子(整式)相加减
分母不变
转化为
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
