北师大版八年级数学下册6.2 平行四边形的判定课件(第1课时 41张)
文档属性
| 名称 | 北师大版八年级数学下册6.2 平行四边形的判定课件(第1课时 41张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:16:10 | ||
图片预览











文档简介
北师大版 八年级 数学 下册
6.2 平行四边形的判定
(第1课时)
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
知识回顾:
导入新知
思考:
周末,小明的爸爸带着他回到了老家,看望乡下的爷爷.午饭后,小明的爷爷准备给他心爱的小菜园扎篱笆,地上散落着很多长短不一的细木棒.这时小明的爸爸说:“小明,你们现在已经开始学习平行四边形了,你能不能挑四根细木棒拼一个平行四边形呢?”
(2)他怎样才能拼接成平行四边形?
为什么?
你能为小明出谋划策吗?
(1)他应该选什么规格的细木棒?
导入新知
1. 经历平行四边形判定方法的探究过程,掌握说理的基本方法.
2. 平行四边形判定方法的理解和灵活应用.
素养目标
活动:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
猜测:两组对边分别相等的四边形是平行四边形.
20cm
30cm
探究新知
知识点 1
平行四边形的判定定理1
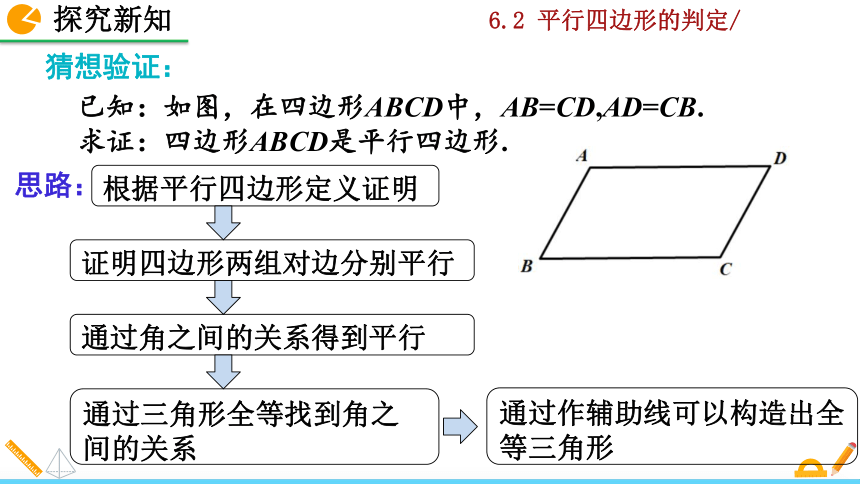
已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
根据平行四边形定义证明
证明四边形两组对边分别平行
通过角之间的关系得到平行
通过三角形全等找到角之间的关系
通过作辅助线可以构造出全等三角形
猜想验证:
思路:
探究新知
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
连接BD,
在△ABD和△CDB中,
AB=CD,
BD=DB,
AD=CB,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥CD , AD∥CB
∴四边形ABCD是平行四边形.
证明:
A
B
C
D
1
4
2
3
探究新知
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1:
B
D
C
A
结论
探究新知
例 如图1,窗框和窗扇用“滑块铰链”连接,图2是图1中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点B,C,D始终在一直线上,延长DE交MN于点F.已知AC=DE=20 cm,AE=CD=10 cm,BD=40 cm.
两组对边分别相等的四边形是平行四边形
素养考点 1
探究新知
(1)窗扇完全打开,张角∠CAB=85°,求此时窗扇与窗框的夹角∠DFB的度数.
(2)窗扇部分打开,张角∠CAB=60°,求此时点A,B之间的距离(精确到0.1 cm).
(参考数据: ≈1.732, ≈2.449)
探究新知
解:(1)∵AC=DE=20 cm,AE=CD=10 cm,
∴四边形ACDE是平行四边形,∴AC∥DE,∴∠DFB=∠CAB,
∵∠CAB=85°,∴∠DFB=85°.
(2)作CG⊥AB于点G,
∵AC=20 cm,∠CGA=90°,∠CAB=60°,
∴AG= AC=10 cm,
CG= cm,
∵BD=40 cm,CD=10 cm,
∴CB=30 cm,
∴BG= (cm),
∴AB=AG+BG=10+10 ≈10+10×2.449=34.49≈34.5(cm),
即A,B之间的距离约为34.5 cm.
探究新知
方法总结
从两边的角度证明平行四边形的方法
(1)两组对边分别_________的四边形是平行四边形.
(2)两组对边分别_____的四边形是平行四边形.?
平行
相等
探究新知
如图所示,平行四边形ABCD中,AE=CG,DH=BF,则四边形EFGH是 .
平行四边形
巩固练习
变式训练
小明的爸爸又考验小明:“小明啊,如果只用两根相等的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?”
(2)如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?
(1)你认为小明能做到吗?
探究新知
平行四边形的判定定理2
知识点 2
思考:
A
B
C
D
猜想:
一组对边 的四边形是平行四边形.
平行且相等
探究新知
将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
思考:
探究新知
证明方法1:根据平行四边形定义证明
你能想到几种证明方法?
证明方法2:根据两组对边分别相等的四边形是平行四边证明
连接四边形对角线
构造全等三角形
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
猜想验证:
探究新知
证明:连接AC.
∵ AB∥CD,
∴ ∠BAC=∠DCA.
又∵ AB=CD , AC=CA,
∴ △BAC≌△DCA.
∴ ∠ACB=∠CAD.
∴ 四边形ABCD是平行四边形.
∴ BC∥DA.
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
方法1:
探究新知
证明:连接AC.
∵ AB∥CD,
∴ ∠BAC=∠DCA.
又∵ AB=CD AC=CA,
∴ △BAC≌△DCA.
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
方法2:
探究新知
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
结论
探究新知
例1 如图,在平行四边形ABCD中,已知AE,CF分别是∠DAB,
∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE,CF分别是∠DAB, ∠BCD的角平分线,
∴∠B=∠D,AB=CD, AD∥BC,
∠BAE=∠DCF= ∠DAB= ∠BCD.
∴△ABE≌△CDF(ASA).
∴BE=DF.∴AF=CE. ∵AF∥CE,
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形
素养考点 2
探究新知
如图,AC//DE,点B在AC上,且AB=DE=BC.找出图中的平行四边形,并说明理由.
解:∵AC//DE且AB=DE,
∴四边形ABDE是平行四边形.
∵AC//DE且DE=BC,
∴四边形BCDE是平行四边形.
巩固练习
变式训练
如图,在平行四边形ABCD中,E,F分别是AD和BC的中点.
求证:四边形BFDE是平行四边形.
证明:
∵ 四边形ABCD是平行四边形,
∴ AD=CB, AD//BC.
又∵E,F分别是AD和CB的中点,
∴ ED=FB,ED∥FB.
∴ 四边形BFDE是平行四边形.
∴ ED= AD, BF= BC.
例2
探究新知
方法总结
从边的角度判定平行四边形的“两点注意”
(1)已知两组对边:可以通过判定这两组对边分别平行,也可以通过判定这两组对边分别相等来证明四边形是平行四边形.
(2)已知一组对边:需要证明这一组对边平行且相等.
探究新知
四边形ABCD中,AB=CD,AB∥CD,则下列结论中错误的是 ( )
A.∠A=∠C B.AD∥BC
C.∠A=∠B D.对角线互相平分
C
巩固练习
变式训练
我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
探究新知
知识点 3
由定义拓展判定平行四边形
思考:
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°.
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
定义拓展判定:
两组对角分别相等的四边形是平行四边形.
验证:
探究新知
已知:如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:四边形ABCD是平行四边形.
1
2
证明1:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,CA=AC,
∴△ABC≌△CDA.
∴AB=DC,BC=DA.
∴四边形ABCD是平行四边形.
巩固练习
证明2:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,CA=AC,
∴△ABC≌△CDA.
∴AB=CD,AB∥CD.
∴四边形ABCD是平行四边形.
巩固练习
1
2
证明3:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,
∴∠BCA=∠DAC.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
连接中考
(2020·鸡西)如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
AB∥CD(答案不唯一)
1.在四边形ABCD中,若AD=8,AB=4,那么当BC=______,
CD=______时,四边形ABCD是平行四边形.?
8
4
课堂检测
基础巩固题
2.如图所示,在四边形ABCD中,AD∥CB,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C向B运动,则______秒后四边形ABQP为平行四边形. ?
2
课堂检测
基础巩固题
3.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列添加的条件不正确的是( )
B
A.AB=CD B.BC=AD
C.∠A=∠C D.BC∥AD
课堂检测
基础巩固题
4.如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )
B
A.AB=CD B.∠BAD=∠DCB
C.AC=BD D.∠ABC+∠BAD=180°
课堂检测
基础巩固题
5.如图,在平行四边形ABCD中,E,F分别是AB,CD上的点,且EF∥BC,DE∥BF,则图中共有______个平行四边形.(平行四边形ABCD除外).?
3
课堂检测
基础巩固题
1.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明: ∵BD是△ABC的角平分线,
∴∠ABD=∠DBE.
∵DE∥AB,
∴∠ABD=∠BDE.
∴∠DBE=∠BDE.∴BE=DE.
∵BE=AF,∴AF=DE.
∵AF∥DE,
∴四边形ADEF是平行四边形.
课堂检测
能力提升题
2.如图,已知△ABC,分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE,△BCD,△ACF,求证:四边形DEAF是平行四边形.
证明: ∵△ABE,△BDC都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°-∠DBA,∠ABC=60°-∠DBA,
∴∠DBE=∠ABC.在△DBE和△ABC中,
∴△DBE≌△CBA(SAS),∴DE=AC.
课堂检测
能力提升题
又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FDC,∴DF=AB=AE.
∵DE=AF,EA=DF,∴四边形DEAF为平行四边形.
如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:四边形DEBF是平行四边形.
拓广探索题
课堂检测
证明:方法一:(利用两组对边分别相等)
∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF,∴DE=BF,
同理可得,△ABE≌△CDF,∴BE=DF,
∴四边形DEBF是平行四边形.
课堂检测
方法二:(利用一组对边平行且相等)
∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF.∴DE=BF,∠ADE=∠CBF.
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE.∴DE∥BF.又∵DE=BF,
∴四边形DEBF是平行四边形.
课堂检测
平行四边形的判定
定义拓展法
判定定理1
判定定理2
①已知一组对边平行,可以证另一组对边平行;也可证这组对边相等.
②已知一组对边相等,可以证另一组对边相等;也可证这组对边平行.
③已知一组对角相等,再证另一组对角相等.
课堂小结
6.2 平行四边形的判定
(第1课时)
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
对称性
平行四边形是中心对称图形
对角线
知识回顾:
导入新知
思考:
周末,小明的爸爸带着他回到了老家,看望乡下的爷爷.午饭后,小明的爷爷准备给他心爱的小菜园扎篱笆,地上散落着很多长短不一的细木棒.这时小明的爸爸说:“小明,你们现在已经开始学习平行四边形了,你能不能挑四根细木棒拼一个平行四边形呢?”
(2)他怎样才能拼接成平行四边形?
为什么?
你能为小明出谋划策吗?
(1)他应该选什么规格的细木棒?
导入新知
1. 经历平行四边形判定方法的探究过程,掌握说理的基本方法.
2. 平行四边形判定方法的理解和灵活应用.
素养目标
活动:用两根长30cm的木条和两根长20cm的木条作为四边形的四条边,能否拼成一个平行四边形?与同伴进行交流.
猜测:两组对边分别相等的四边形是平行四边形.
20cm
30cm
探究新知
知识点 1
平行四边形的判定定理1
已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:四边形ABCD是平行四边形.
根据平行四边形定义证明
证明四边形两组对边分别平行
通过角之间的关系得到平行
通过三角形全等找到角之间的关系
通过作辅助线可以构造出全等三角形
猜想验证:
思路:
探究新知
已知: 四边形ABCD中,AB=CD,AD=CB.
求证: 四边形ABCD是平行四边形.
连接BD,
在△ABD和△CDB中,
AB=CD,
BD=DB,
AD=CB,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥CD , AD∥CB
∴四边形ABCD是平行四边形.
证明:
A
B
C
D
1
4
2
3
探究新知
两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理1:
B
D
C
A
结论
探究新知
例 如图1,窗框和窗扇用“滑块铰链”连接,图2是图1中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,交点A处装有滑块,滑块可以左右滑动,支点B,C,D始终在一直线上,延长DE交MN于点F.已知AC=DE=20 cm,AE=CD=10 cm,BD=40 cm.
两组对边分别相等的四边形是平行四边形
素养考点 1
探究新知
(1)窗扇完全打开,张角∠CAB=85°,求此时窗扇与窗框的夹角∠DFB的度数.
(2)窗扇部分打开,张角∠CAB=60°,求此时点A,B之间的距离(精确到0.1 cm).
(参考数据: ≈1.732, ≈2.449)
探究新知
解:(1)∵AC=DE=20 cm,AE=CD=10 cm,
∴四边形ACDE是平行四边形,∴AC∥DE,∴∠DFB=∠CAB,
∵∠CAB=85°,∴∠DFB=85°.
(2)作CG⊥AB于点G,
∵AC=20 cm,∠CGA=90°,∠CAB=60°,
∴AG= AC=10 cm,
CG= cm,
∵BD=40 cm,CD=10 cm,
∴CB=30 cm,
∴BG= (cm),
∴AB=AG+BG=10+10 ≈10+10×2.449=34.49≈34.5(cm),
即A,B之间的距离约为34.5 cm.
探究新知
方法总结
从两边的角度证明平行四边形的方法
(1)两组对边分别_________的四边形是平行四边形.
(2)两组对边分别_____的四边形是平行四边形.?
平行
相等
探究新知
如图所示,平行四边形ABCD中,AE=CG,DH=BF,则四边形EFGH是 .
平行四边形
巩固练习
变式训练
小明的爸爸又考验小明:“小明啊,如果只用两根相等的细木棒,你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢?”
(2)如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形?
(1)你认为小明能做到吗?
探究新知
平行四边形的判定定理2
知识点 2
思考:
A
B
C
D
猜想:
一组对边 的四边形是平行四边形.
平行且相等
探究新知
将两根同样长的木条AD,BC平行放置,再用木条AB,DC加固,得到的四边形ABCD是平行四边形.
A
B
C
D
猜想:一组对边平行且相等的四边形是平行四边形.
思考:
探究新知
证明方法1:根据平行四边形定义证明
你能想到几种证明方法?
证明方法2:根据两组对边分别相等的四边形是平行四边证明
连接四边形对角线
构造全等三角形
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
猜想验证:
探究新知
证明:连接AC.
∵ AB∥CD,
∴ ∠BAC=∠DCA.
又∵ AB=CD , AC=CA,
∴ △BAC≌△DCA.
∴ ∠ACB=∠CAD.
∴ 四边形ABCD是平行四边形.
∴ BC∥DA.
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
方法1:
探究新知
证明:连接AC.
∵ AB∥CD,
∴ ∠BAC=∠DCA.
又∵ AB=CD AC=CA,
∴ △BAC≌△DCA.
∴ BC=AD.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB CD.求证:四边形ABCD是平行四边形.
方法2:
探究新知
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,
AB∥CD,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
结论
探究新知
例1 如图,在平行四边形ABCD中,已知AE,CF分别是∠DAB,
∠BCD的角平分线,试证明四边形AFCE是平行四边形.
证明:∵在平行四边形ABCD中,
AE,CF分别是∠DAB, ∠BCD的角平分线,
∴∠B=∠D,AB=CD, AD∥BC,
∠BAE=∠DCF= ∠DAB= ∠BCD.
∴△ABE≌△CDF(ASA).
∴BE=DF.∴AF=CE. ∵AF∥CE,
∴四边形AFCE是平行四边形(一组对边平行且相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形
素养考点 2
探究新知
如图,AC//DE,点B在AC上,且AB=DE=BC.找出图中的平行四边形,并说明理由.
解:∵AC//DE且AB=DE,
∴四边形ABDE是平行四边形.
∵AC//DE且DE=BC,
∴四边形BCDE是平行四边形.
巩固练习
变式训练
如图,在平行四边形ABCD中,E,F分别是AD和BC的中点.
求证:四边形BFDE是平行四边形.
证明:
∵ 四边形ABCD是平行四边形,
∴ AD=CB, AD//BC.
又∵E,F分别是AD和CB的中点,
∴ ED=FB,ED∥FB.
∴ 四边形BFDE是平行四边形.
∴ ED= AD, BF= BC.
例2
探究新知
方法总结
从边的角度判定平行四边形的“两点注意”
(1)已知两组对边:可以通过判定这两组对边分别平行,也可以通过判定这两组对边分别相等来证明四边形是平行四边形.
(2)已知一组对边:需要证明这一组对边平行且相等.
探究新知
四边形ABCD中,AB=CD,AB∥CD,则下列结论中错误的是 ( )
A.∠A=∠C B.AD∥BC
C.∠A=∠B D.对角线互相平分
C
巩固练习
变式训练
我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
探究新知
知识点 3
由定义拓展判定平行四边形
思考:
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
A
B
C
D
又∵∠A=∠C,∠B=∠D,
∵∠A+∠C+∠B+∠D=360°,
∴2∠A+2∠B=360°,
即∠A+∠B=180°.
∴ AD∥BC.
∴四边形ABCD是平行四边形.
同理得 AB∥ CD,
证明:
定义拓展判定:
两组对角分别相等的四边形是平行四边形.
验证:
探究新知
已知:如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:四边形ABCD是平行四边形.
1
2
证明1:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,CA=AC,
∴△ABC≌△CDA.
∴AB=DC,BC=DA.
∴四边形ABCD是平行四边形.
巩固练习
证明2:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,CA=AC,
∴△ABC≌△CDA.
∴AB=CD,AB∥CD.
∴四边形ABCD是平行四边形.
巩固练习
1
2
证明3:在△ABC和△CDA中,
∵∠B=∠D,∠1=∠2,
∴∠BCA=∠DAC.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形.
连接中考
(2020·鸡西)如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
AB∥CD(答案不唯一)
1.在四边形ABCD中,若AD=8,AB=4,那么当BC=______,
CD=______时,四边形ABCD是平行四边形.?
8
4
课堂检测
基础巩固题
2.如图所示,在四边形ABCD中,AD∥CB,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2 cm/s的速度由C向B运动,则______秒后四边形ABQP为平行四边形. ?
2
课堂检测
基础巩固题
3.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列添加的条件不正确的是( )
B
A.AB=CD B.BC=AD
C.∠A=∠C D.BC∥AD
课堂检测
基础巩固题
4.如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )
B
A.AB=CD B.∠BAD=∠DCB
C.AC=BD D.∠ABC+∠BAD=180°
课堂检测
基础巩固题
5.如图,在平行四边形ABCD中,E,F分别是AB,CD上的点,且EF∥BC,DE∥BF,则图中共有______个平行四边形.(平行四边形ABCD除外).?
3
课堂检测
基础巩固题
1.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.求证:四边形ADEF是平行四边形.
证明: ∵BD是△ABC的角平分线,
∴∠ABD=∠DBE.
∵DE∥AB,
∴∠ABD=∠BDE.
∴∠DBE=∠BDE.∴BE=DE.
∵BE=AF,∴AF=DE.
∵AF∥DE,
∴四边形ADEF是平行四边形.
课堂检测
能力提升题
2.如图,已知△ABC,分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE,△BCD,△ACF,求证:四边形DEAF是平行四边形.
证明: ∵△ABE,△BDC都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°-∠DBA,∠ABC=60°-∠DBA,
∴∠DBE=∠ABC.在△DBE和△ABC中,
∴△DBE≌△CBA(SAS),∴DE=AC.
课堂检测
能力提升题
又∵△ACF是等边三角形,∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FDC,∴DF=AB=AE.
∵DE=AF,EA=DF,∴四边形DEAF为平行四边形.
如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:四边形DEBF是平行四边形.
拓广探索题
课堂检测
证明:方法一:(利用两组对边分别相等)
∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF,∴DE=BF,
同理可得,△ABE≌△CDF,∴BE=DF,
∴四边形DEBF是平行四边形.
课堂检测
方法二:(利用一组对边平行且相等)
∵四边形ABCD是平行四边形,∴AD∥CB,AD=CB,
∴∠DAE=∠BCF.
在△ADE和△CBF中,
∴△ADE≌△CBF.∴DE=BF,∠ADE=∠CBF.
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE.∴DE∥BF.又∵DE=BF,
∴四边形DEBF是平行四边形.
课堂检测
平行四边形的判定
定义拓展法
判定定理1
判定定理2
①已知一组对边平行,可以证另一组对边平行;也可证这组对边相等.
②已知一组对边相等,可以证另一组对边相等;也可证这组对边平行.
③已知一组对角相等,再证另一组对角相等.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
