北师大版八年级数学下册6.2 平行四边形的判定课件(第2课时 23张)
文档属性
| 名称 | 北师大版八年级数学下册6.2 平行四边形的判定课件(第2课时 23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 454.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览


文档简介
北师大版 八年级 数学 下册
6.2 平行四边形的判定
(第2课时)
判定
定理1
定理2
定义拓展法
文字语言
图形语言
符号语言
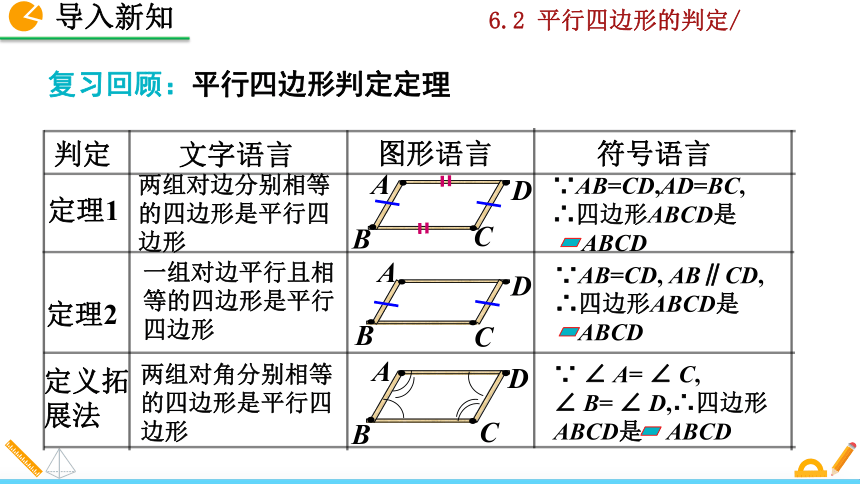
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
复习回顾:平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵AB=CD, AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
∵ ∠ A= ∠ C,
∠ B= ∠ D,∴四边形ABCD是 ABCD
导入新知
1. 利用对角线互相平分判定平行四边形.
2. 掌握平行四边形判定的方法.
素养目标
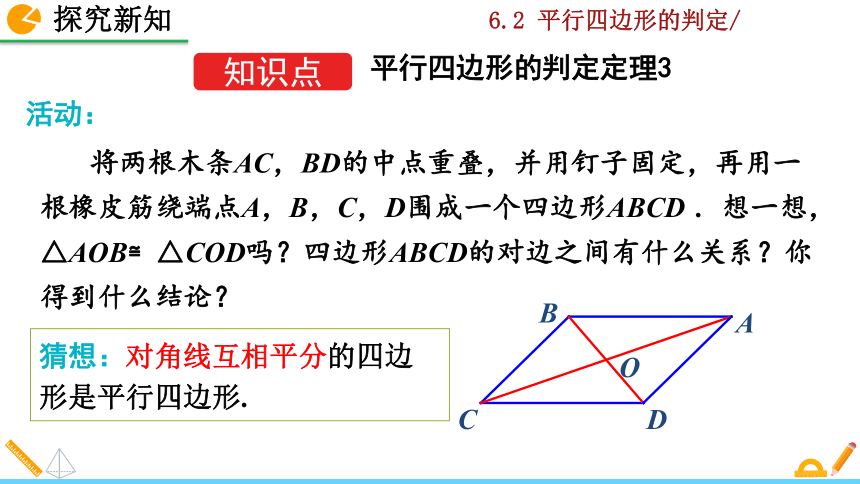
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
探究新知
知识点
平行四边形的判定定理3
活动:
A
B
C
D
O
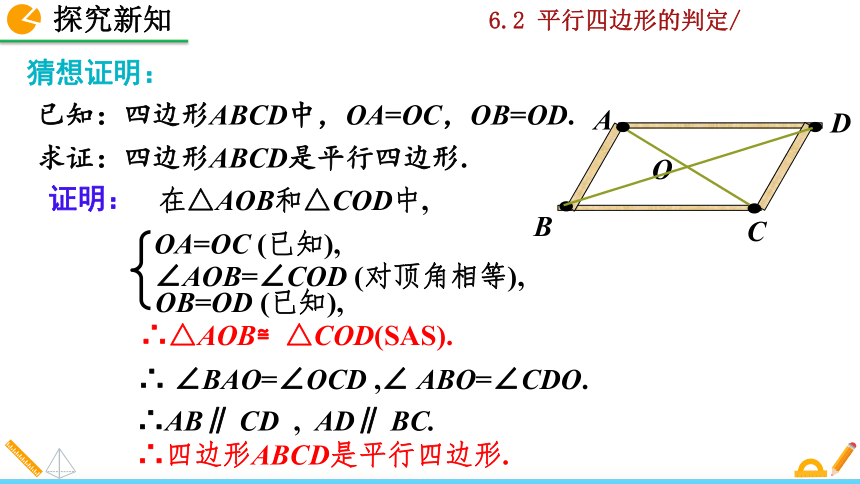
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
猜想证明:
探究新知
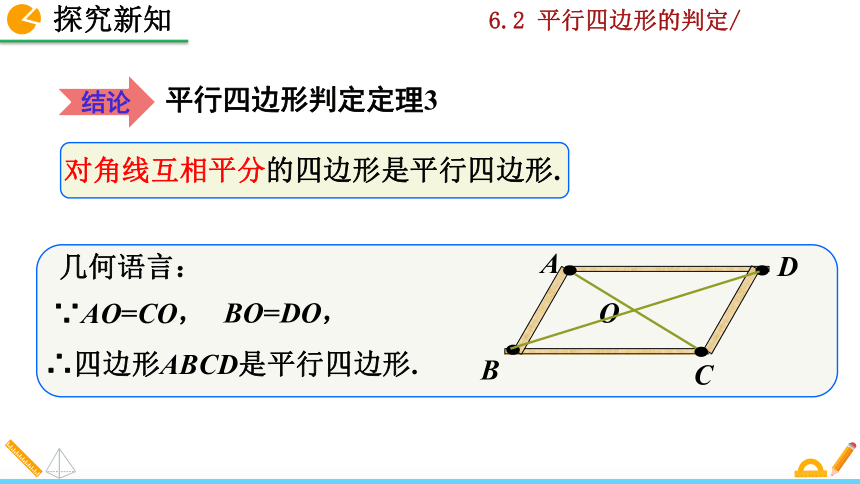
对角线互相平分的四边形是平行四边形.
∵AO=CO,
BO=DO,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理3
A
B
C
D
O
结论
探究新知
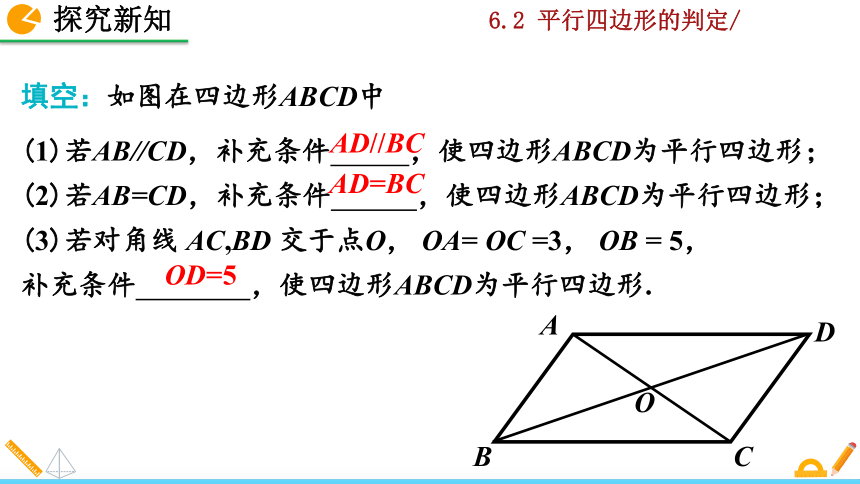
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形;
(3)若对角线 AC,BD 交于点O, OA= OC =3, OB = 5,
补充条件 ,使四边形ABCD为平行四边形.
AD//BC
AD=BC
OD=5
B
O
D
A
C
探究新知
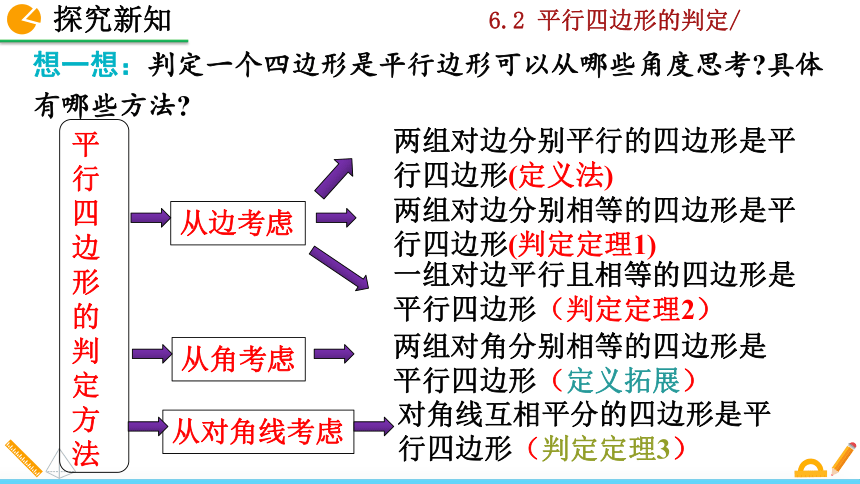
想一想:判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
探究新知
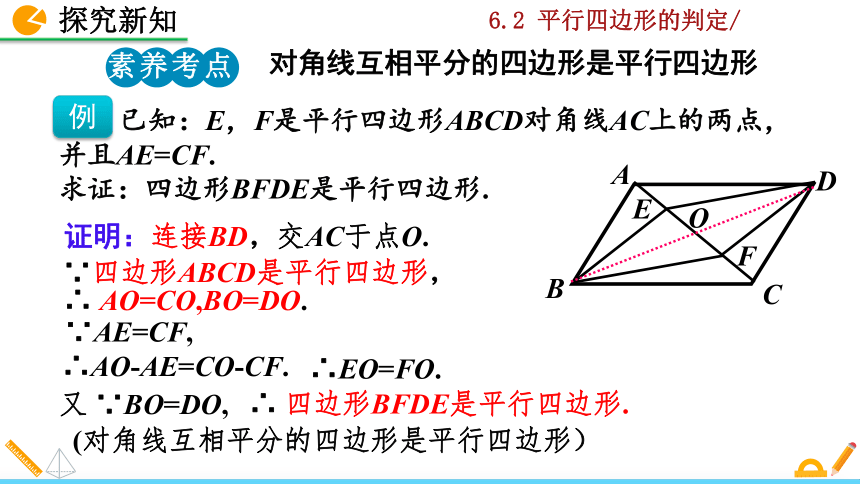
已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF,
∴AO-AE=CO-CF.
∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
O
B
A
C
E
F
D
对角线互相平分的四边形是平行四边形
素养考点 1
探究新知
例
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
判定平行四边形的方法选择
已知条件
证明思路
一组对边相等
1.另一组对边也相等
2.相等的边也平行
一组对边平行
1.另一组对边也平行
2.平行的边也相等
对角线相交
对角线互相平分
探究新知
如图,已知G,H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG,FH交于点D,连接AD,DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
巩固练习
变式训练
证明: ∵GE∥BH,HF∥BG,∴四边形BHDG是平行四边形.
∴OB= OD,OG= OH.?
∵G,H是△ABC的边AC的三等分点,∴AG=GH=CH.
∴OG+ AG =OH+ CH, ?∴OA= OC,?
∴四边形ABCD是平行四边形.
巩固练习
根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
C
D
A
B
C
巩固练习
变式训练
连接中考
(2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AB∥DC,AD=BC
D. OA=OC,OB=OD
C
1.若AC=10,BD=8,AC与BD相交于点O,那么当AO=______,DO=______时,四边形ABCD是平行四边形.?
5
4
课堂检测
基础巩固题
2.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
课堂检测
基础巩固题
3.如图,在△ABC中,D是AB边上任意一点,E是BC边中点,CF∥AB,交DE的延长线于点F,连接BF,CD.
求证:四边形CDBF是平行四边形.
证明:∵CF∥AB,∴∠ECF=∠EBD,
∵E是BC的中点,∴CE=BE,
∵∠CEF=∠BED,∴△CEF≌△BED(ASA),
∴EF=ED,∴四边形CDBF是平行四边形.
课堂检测
基础巩固题
已知:如图,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F,直线GH过点O,分别交AB,CD于点G,H.
求证:四边形EGFH是平行四边形.
课堂检测
能力提升题
证明:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),∴EO=FO,
同理可得:△BGO≌△DHO,∴GO=HO,
∴四边形EGFH是平行四边形.
课堂检测
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
拓广探索题
课堂检测
证明:方法一:(根据对角线互相平分)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AE=EF,又∵BE=CE,
∴四边形ABFC是平行四边形.
课堂检测
方法二:(根据一组对边平行且相等)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AB=FC,
又∵AB∥CD,∴四边形ABFC是平行四边形.
课堂检测
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
课堂小结
6.2 平行四边形的判定
(第2课时)
判定
定理1
定理2
定义拓展法
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
复习回顾:平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵AB=CD, AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
∵ ∠ A= ∠ C,
∠ B= ∠ D,∴四边形ABCD是 ABCD
导入新知
1. 利用对角线互相平分判定平行四边形.
2. 掌握平行四边形判定的方法.
素养目标
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
探究新知
知识点
平行四边形的判定定理3
活动:
A
B
C
D
O
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
证明:
在△AOB和△COD中,
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO=∠OCD ,∠ ABO=∠CDO.
∴AB∥ CD , AD∥ BC.
∴四边形ABCD是平行四边形.
猜想证明:
探究新知
对角线互相平分的四边形是平行四边形.
∵AO=CO,
BO=DO,
∴四边形ABCD是平行四边形.
几何语言:
平行四边形判定定理3
A
B
C
D
O
结论
探究新知
填空:如图在四边形ABCD中
(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形;
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形;
(3)若对角线 AC,BD 交于点O, OA= OC =3, OB = 5,
补充条件 ,使四边形ABCD为平行四边形.
AD//BC
AD=BC
OD=5
B
O
D
A
C
探究新知
想一想:判定一个四边形是平行边形可以从哪些角度思考?具体有哪些方法?
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
探究新知
已知:E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
证明:连接BD,交AC于点O.
∵AE=CF,
∴AO-AE=CO-CF.
∴EO=FO.
又 ∵BO=DO,
∴ 四边形BFDE是平行四边形.
(对角线互相平分的四边形是平行四边形)
O
B
A
C
E
F
D
对角线互相平分的四边形是平行四边形
素养考点 1
探究新知
例
∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
判定平行四边形的方法选择
已知条件
证明思路
一组对边相等
1.另一组对边也相等
2.相等的边也平行
一组对边平行
1.另一组对边也平行
2.平行的边也相等
对角线相交
对角线互相平分
探究新知
如图,已知G,H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG,FH交于点D,连接AD,DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
巩固练习
变式训练
证明: ∵GE∥BH,HF∥BG,∴四边形BHDG是平行四边形.
∴OB= OD,OG= OH.?
∵G,H是△ABC的边AC的三等分点,∴AG=GH=CH.
∴OG+ AG =OH+ CH, ?∴OA= OC,?
∴四边形ABCD是平行四边形.
巩固练习
根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
C
D
A
B
C
巩固练习
变式训练
连接中考
(2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AB∥DC,AD=BC
D. OA=OC,OB=OD
C
1.若AC=10,BD=8,AC与BD相交于点O,那么当AO=______,DO=______时,四边形ABCD是平行四边形.?
5
4
课堂检测
基础巩固题
2.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
课堂检测
基础巩固题
3.如图,在△ABC中,D是AB边上任意一点,E是BC边中点,CF∥AB,交DE的延长线于点F,连接BF,CD.
求证:四边形CDBF是平行四边形.
证明:∵CF∥AB,∴∠ECF=∠EBD,
∵E是BC的中点,∴CE=BE,
∵∠CEF=∠BED,∴△CEF≌△BED(ASA),
∴EF=ED,∴四边形CDBF是平行四边形.
课堂检测
基础巩固题
已知:如图,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F,直线GH过点O,分别交AB,CD于点G,H.
求证:四边形EGFH是平行四边形.
课堂检测
能力提升题
证明:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),∴EO=FO,
同理可得:△BGO≌△DHO,∴GO=HO,
∴四边形EGFH是平行四边形.
课堂检测
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
拓广探索题
课堂检测
证明:方法一:(根据对角线互相平分)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AE=EF,又∵BE=CE,
∴四边形ABFC是平行四边形.
课堂检测
方法二:(根据一组对边平行且相等)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AB=FC,
又∵AB∥CD,∴四边形ABFC是平行四边形.
课堂检测
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
