北师大版八年级数学下册6.4 多边形的内角和与外角和课件(第1课时 22张)
文档属性
| 名称 | 北师大版八年级数学下册6.4 多边形的内角和与外角和课件(第1课时 22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 718.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 21:14:37 | ||
图片预览




文档简介
6.4 多边形的内角和与外角和
(第1课时)
北师大版 八年级 数学 下册
法国的建筑事务所atelierd将协调坚固的蜂窝与人类天马行空的想象力结合,创造了这个“abeilles bee pavilion”.
思考:你知道正六边形的内角和是多少吗?
导入新知
1. 经历探索多边形内角和的过程,掌握多边形内角和公式.
2. 灵活运用公式进行内角和的计算 ,并且会计算正多边形的一个内角的度数.
素养目标
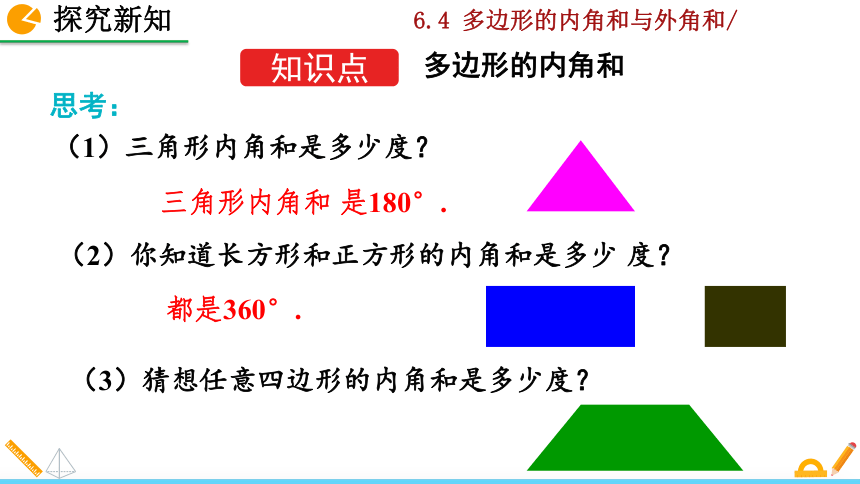
(2)你知道长方形和正方形的内角和是多少 度?
(1)三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
(3)猜想任意四边形的内角和是多少度?
思考:
探究新知
知识点
多边形的内角和
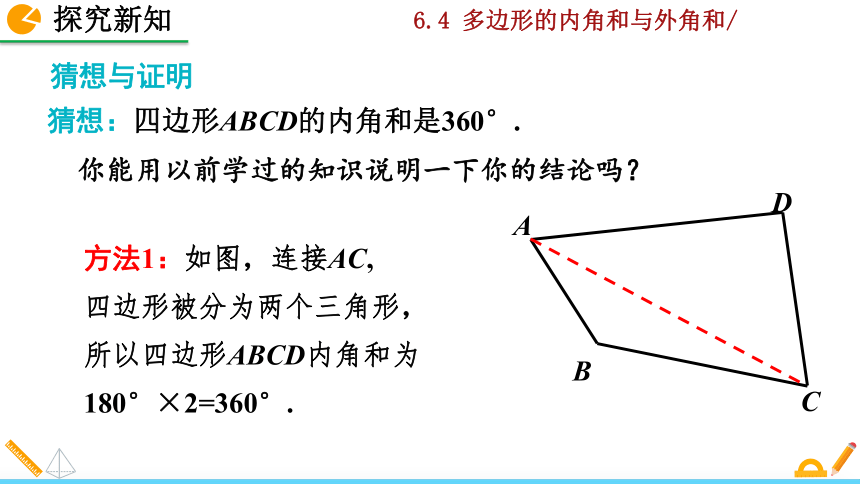
猜想:四边形ABCD的内角和是360°.
你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法1:如图,连接AC,
四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
探究新知
A
B
C
D
E
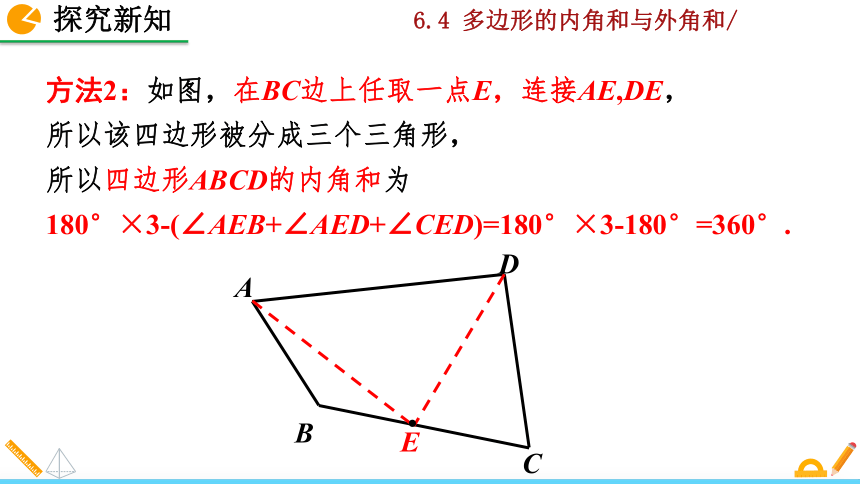
方法2:如图,在BC边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
探究新知
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
探究新知
A
B
C
D
P
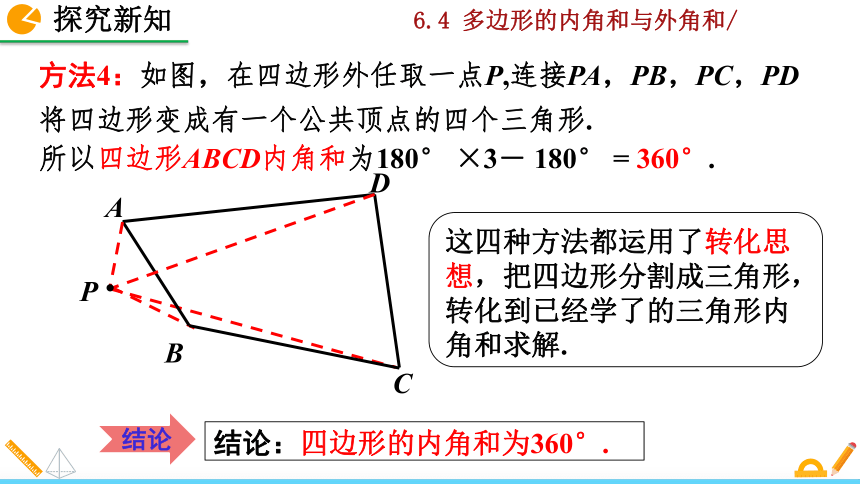
方法4:如图,在四边形外任取一点P,连接PA,PB,PC,PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180° ×3- 180° = 360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论:四边形的内角和为360°.
结论
探究新知
A
C
D
E
B
A
B
C
D
E
F
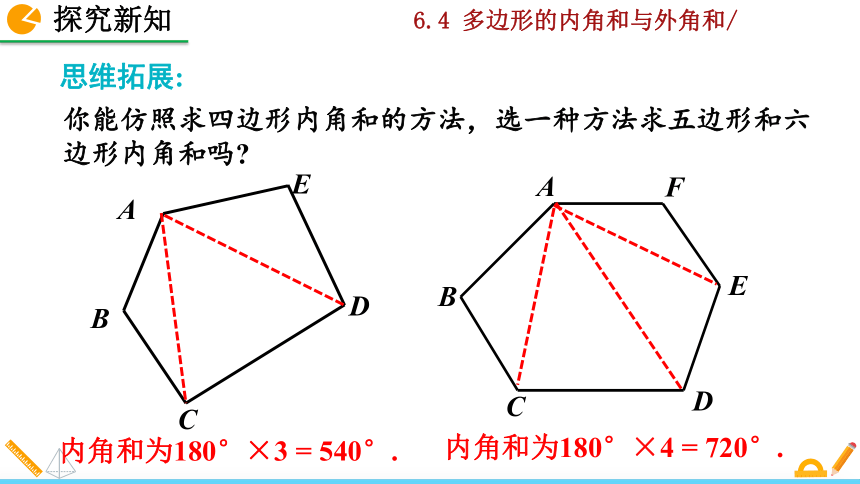
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
内角和为180°×3 = 540°.
内角和为180°×4 = 720°.
思维拓展:
探究新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
由特殊到一般
探究新知
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
结论
探究新知
如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
∵
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
∴
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
多边形的内角和定理
素养考点
探究新知
例
结论
方法总结
多边形内角和的三点注意
(1)多边形的内角和是指n个内角的度数之和.
(2)多边形的内角和为(n-2)·180°,且内角和为180°的整数倍.
(3)由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
探究新知
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A.50° B.55° C.60° D.65°
C
巩固练习
变式训练
连接中考
(2020·德阳)多边形的内角和不可能为 ( )
A.180° B.540°
C.1080° D.1200°
D
1.六边形的内角和是 ( )
A.540° B.720° C.900° D.1080°
B
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
C
课堂检测
基础巩固题
3. 多边形的边数由6增加到9,内角和增加 度.
540
解:法1:六边形内角和为(6-2) ×180°= 720 °,
九边形内角和为(9-2) ×180°= 1260 °,
1260 °- 720 °=540°.
法2:设六边形内角和为(n-2) ×180°,
则九边形内角和为(n+3-2) ×180°,
(n+3-2) ×180-(n-2) ×180=3 × 180°=540°.
注意:多边形的边数增加1,内角和就增加180度.
课堂检测
基础巩固题
4.已知n边形的内角和θ=(n-2)×180°.
(1)当θ=720°时,求出边数n.
(2)小明说,θ能取820°,这种说法对吗?若对,求出边数n;若不对,说明理由.
解:(1)720°=(n-2)×180°,n-2=4,n=6.
(2)小明的说法不对.
理由:∵当θ取820°时,820°=(n-2)×180°,
解得:n= ,
∵n应为整数,∴θ不能取820°,
故小明的说法不对.
课堂检测
基础巩固题
1.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)×180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
课堂检测
能力提升题
2.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为( )
A.540° B.720° C.900° D.1260°
课堂检测
C
能力提升题
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°.
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°.
∵BE∥DF,∴∠EBF=∠CFD.
∴∠CDF+∠CFD=90°,故△DCF为直角三角形.
课堂检测
拓广探索题
多边形内角和
转化
从特殊到一般
方程
(n-2) ·180°
数学思想
公式
方法
已知边数求内角和:代入法
已知内角和求边数:方程法
课堂小结
(第1课时)
北师大版 八年级 数学 下册
法国的建筑事务所atelierd将协调坚固的蜂窝与人类天马行空的想象力结合,创造了这个“abeilles bee pavilion”.
思考:你知道正六边形的内角和是多少吗?
导入新知
1. 经历探索多边形内角和的过程,掌握多边形内角和公式.
2. 灵活运用公式进行内角和的计算 ,并且会计算正多边形的一个内角的度数.
素养目标
(2)你知道长方形和正方形的内角和是多少 度?
(1)三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
(3)猜想任意四边形的内角和是多少度?
思考:
探究新知
知识点
多边形的内角和
猜想:四边形ABCD的内角和是360°.
你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法1:如图,连接AC,
四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
探究新知
A
B
C
D
E
方法2:如图,在BC边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
探究新知
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
探究新知
A
B
C
D
P
方法4:如图,在四边形外任取一点P,连接PA,PB,PC,PD将四边形变成有一个公共顶点的四个三角形.
所以四边形ABCD内角和为180° ×3- 180° = 360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论:四边形的内角和为360°.
结论
探究新知
A
C
D
E
B
A
B
C
D
E
F
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
内角和为180°×3 = 540°.
内角和为180°×4 = 720°.
思维拓展:
探究新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
由特殊到一般
探究新知
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
多边形的内角和公式
n边形内角和等于(n-2)×180 °.
结论
探究新知
如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D=(4-2) ×180 °= 360 °,
∵
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
∴
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
多边形的内角和定理
素养考点
探究新知
例
结论
方法总结
多边形内角和的三点注意
(1)多边形的内角和是指n个内角的度数之和.
(2)多边形的内角和为(n-2)·180°,且内角和为180°的整数倍.
(3)由多边形的边数可以求出其内角和,由多边形的内角和也可以求出多边形的边数.
探究新知
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P的度数是( )
A.50° B.55° C.60° D.65°
C
巩固练习
变式训练
连接中考
(2020·德阳)多边形的内角和不可能为 ( )
A.180° B.540°
C.1080° D.1200°
D
1.六边形的内角和是 ( )
A.540° B.720° C.900° D.1080°
B
2.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
C
课堂检测
基础巩固题
3. 多边形的边数由6增加到9,内角和增加 度.
540
解:法1:六边形内角和为(6-2) ×180°= 720 °,
九边形内角和为(9-2) ×180°= 1260 °,
1260 °- 720 °=540°.
法2:设六边形内角和为(n-2) ×180°,
则九边形内角和为(n+3-2) ×180°,
(n+3-2) ×180-(n-2) ×180=3 × 180°=540°.
注意:多边形的边数增加1,内角和就增加180度.
课堂检测
基础巩固题
4.已知n边形的内角和θ=(n-2)×180°.
(1)当θ=720°时,求出边数n.
(2)小明说,θ能取820°,这种说法对吗?若对,求出边数n;若不对,说明理由.
解:(1)720°=(n-2)×180°,n-2=4,n=6.
(2)小明的说法不对.
理由:∵当θ取820°时,820°=(n-2)×180°,
解得:n= ,
∵n应为整数,∴θ不能取820°,
故小明的说法不对.
课堂检测
基础巩固题
1.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)×180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
课堂检测
能力提升题
2.过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,则这个多边形的内角和为( )
A.540° B.720° C.900° D.1260°
课堂检测
C
能力提升题
如图,在四边形ABCD中,∠A与∠C互补,BE平分∠ABC,DF平分∠ADC,若BE∥DF,求证:△DCF为直角三角形.
证明:∵在四边形ABCD中,∠A与∠C互补,
∴∠ABC+∠ADC=180°.
∵BE平分∠ABC,DF平分∠ADC,
∴∠CDF+∠EBF=90°.
∵BE∥DF,∴∠EBF=∠CFD.
∴∠CDF+∠CFD=90°,故△DCF为直角三角形.
课堂检测
拓广探索题
多边形内角和
转化
从特殊到一般
方程
(n-2) ·180°
数学思想
公式
方法
已知边数求内角和:代入法
已知内角和求边数:方程法
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
