北师大版八年级数学下册6.4 多边形的内角和与外角和课件(第2课时 23张)
文档属性
| 名称 | 北师大版八年级数学下册6.4 多边形的内角和与外角和课件(第2课时 23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 729.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览




文档简介
北师大版 八年级 数学 下册
6.4 多边形的内角和与外角和
(第2课时)
1.从n边形的一个顶点出发可以引 条对角线,
它们把n边形分成 个三角形.
2.从一个n边形的一个顶点出发可以引5条对角线,则n= . =
3.多边形的内角和公式: .
4.正八边形的每一个内角为: .
(n-3)
(n-2)
8
(n-2)×180°
135°
导入新知
复习回顾:
1. 了解多边形的外角定义,并能准确找出多边形的外角.
2. 掌握多边形的外角和公式,利用内角和与外角和公式解决问题.
素养目标
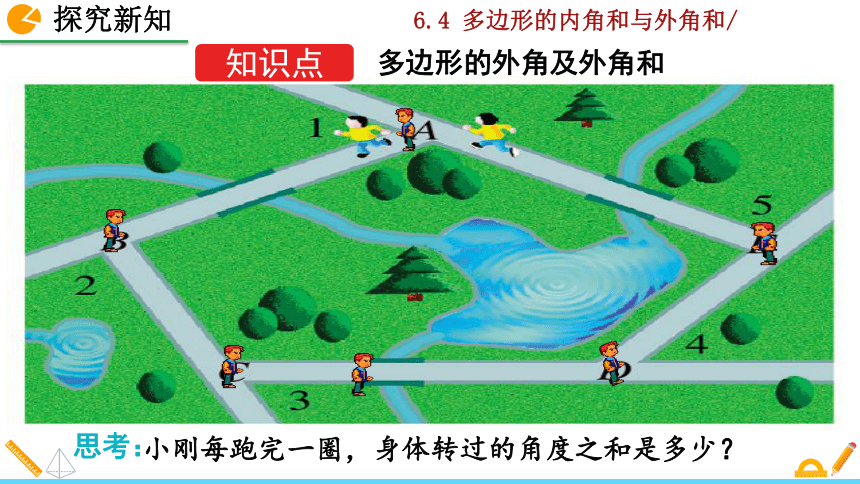
小刚每跑完一圈,身体转过的角度之和是多少?
思考:
探究新知
知识点
多边形的外角及外角和
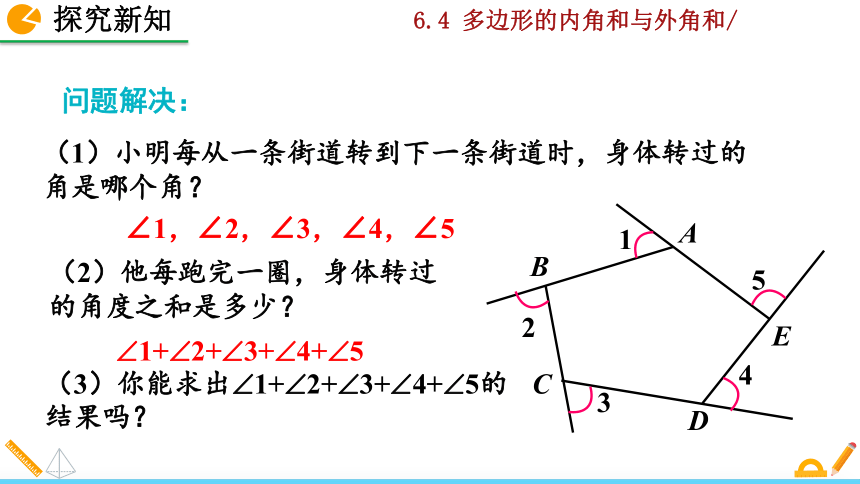
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
E
B
C
D
1
2
3
4
5
A
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能求出?1+?2+?3+?4+?5的结果吗?
∠1,∠2,∠3,∠4,∠5
?1+?2+?3+?4+?5
问题解决:
探究新知
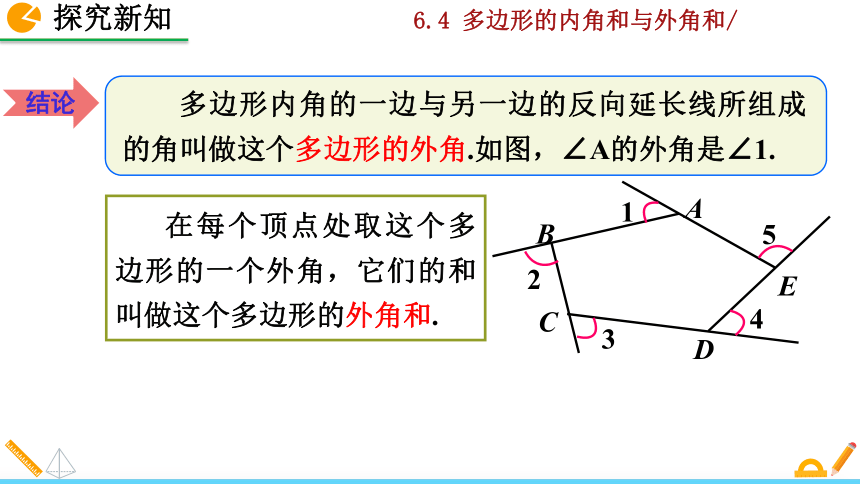
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.如图,∠A的外角是∠1.
E
B
C
D
1
2
3
4
5
A
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
结论
探究新知
如图,在五边形的每个顶点处各取一个外角.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°=900°
思考:
探究新知
E
B
C
D
1
2
3
4
5
A
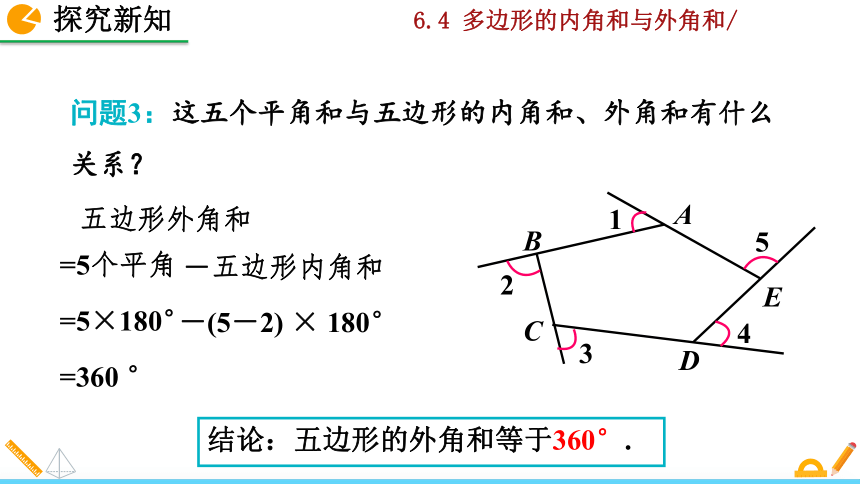
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
探究新知
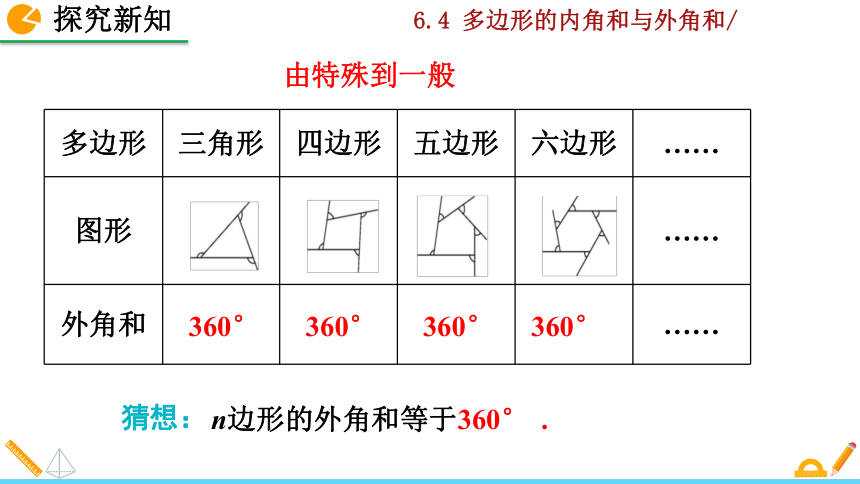
猜想:
360°
360°
360°
360°
由特殊到一般
n边形的外角和等于360° .
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形
三角形
四边形
五边形
六边形
……
图形
……
外角和
……
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
与边数无关
猜想证明:
探究新知
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
拓展思维:
探究新知
方法总结
例1 若正多边形的一个外角是60°,则这个正多边形的内角和是__________.?
720°
多边形的外角和
素养考点 1
探究新知
多边形的外角和不是所有外角的和,是在每一个顶点处取一个外角.多边形的外角和是个定值,不会随边数的变化而变化.
若正多边形的一个内角是150°,则该正多边形的边数是 ( )
A.6 B.12 C.16 D.18
B
巩固练习
变式训练
一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,
则它的内角和为(n-2)·180°,外角和为360°.
则根据题意,得(n-2)·180°=3×360°.
解得n=8,所以这个多边形是八边形.
例2
探究新知
一个正多边形,它的一个外角等于与它相邻的内角的 ,则这个多边形是( )
A.正十二边形 B.正十边形
C.正八边形 D.正六边形
B
巩固练习
变式训练
连接中考
(2020·宜昌)游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右边偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右边偏108°方向行走
D.每段直路要长
A
1.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )
A.120° B.115°
C.105° D.100°
A
课堂检测
基础巩固题
2.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是______.?
5
3.一个多边形的每个内角都相等,并且其中一个内角比它相邻的外角大100°,求这个多边形的边数.
解:设每个内角度数为x度,则与它相邻的外角度数为180°-x°,
根据题意可得x-(180-x)=100,解得x=140.
所以每个外角为40°,
所以这个多边形的边数为360°÷40°=9.
答:这个多边形的边数为9.
课堂检测
基础巩固题
4.(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.
六
正八
课堂检测
基础巩固题
5.若一个多边形的一个外角与它所有内角和为1 160°,求这个多边形的边数.
解:∵一个多边形的一个外角与它所有内角和为1 160°,
1 160÷180=6……80,
∴n-2=6,解得n=8.
课堂检测
基础巩固题
1.一个n边形的所有内角与它的一个外角的和等于2 000°.求这个外角的度数.
解:2 000÷180=11……20.
故这个外角的度数为20°.
课堂检测
能力提升题
2.某正多边形的一个外角的度数为60°,则这个正多边形的边数为( )
A.6 B.8 C. 10 D. 12
A
如图,AP,CP分别是四边形ABCD的外角∠DAM, ∠DCN的平分线,设∠ABC=α, ∠APC=β,则∠ADC的度数为( )
A.180°-α-β B.α+β
C. α+2β D. 2α+β
C
课堂检测
拓广探索题
多边形的外角及外角和
多边形外角的定义
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
课堂小结
6.4 多边形的内角和与外角和
(第2课时)
1.从n边形的一个顶点出发可以引 条对角线,
它们把n边形分成 个三角形.
2.从一个n边形的一个顶点出发可以引5条对角线,则n= . =
3.多边形的内角和公式: .
4.正八边形的每一个内角为: .
(n-3)
(n-2)
8
(n-2)×180°
135°
导入新知
复习回顾:
1. 了解多边形的外角定义,并能准确找出多边形的外角.
2. 掌握多边形的外角和公式,利用内角和与外角和公式解决问题.
素养目标
小刚每跑完一圈,身体转过的角度之和是多少?
思考:
探究新知
知识点
多边形的外角及外角和
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
E
B
C
D
1
2
3
4
5
A
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能求出?1+?2+?3+?4+?5的结果吗?
∠1,∠2,∠3,∠4,∠5
?1+?2+?3+?4+?5
问题解决:
探究新知
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.如图,∠A的外角是∠1.
E
B
C
D
1
2
3
4
5
A
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
结论
探究新知
如图,在五边形的每个顶点处各取一个外角.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°=900°
思考:
探究新知
E
B
C
D
1
2
3
4
5
A
五边形外角和
=360 °
=5个平角
-五边形内角和
=5×180°
-(5-2) × 180°
结论:五边形的外角和等于360°.
问题3:这五个平角和与五边形的内角和、外角和有什么关系?
探究新知
猜想:
360°
360°
360°
360°
由特殊到一般
n边形的外角和等于360° .
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形
三角形
四边形
五边形
六边形
……
图形
……
外角和
……
n边形外角和
n边形的外角和等于360°.
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
与边数无关
猜想证明:
探究新知
回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
拓展思维:
探究新知
方法总结
例1 若正多边形的一个外角是60°,则这个正多边形的内角和是__________.?
720°
多边形的外角和
素养考点 1
探究新知
多边形的外角和不是所有外角的和,是在每一个顶点处取一个外角.多边形的外角和是个定值,不会随边数的变化而变化.
若正多边形的一个内角是150°,则该正多边形的边数是 ( )
A.6 B.12 C.16 D.18
B
巩固练习
变式训练
一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,
则它的内角和为(n-2)·180°,外角和为360°.
则根据题意,得(n-2)·180°=3×360°.
解得n=8,所以这个多边形是八边形.
例2
探究新知
一个正多边形,它的一个外角等于与它相邻的内角的 ,则这个多边形是( )
A.正十二边形 B.正十边形
C.正八边形 D.正六边形
B
巩固练习
变式训练
连接中考
(2020·宜昌)游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路后回到起点,要求每走完一段直路后向右边偏行,成功的招数不止一招,可助我们成功的一招是( )
A.每走完一段直路后沿向右边偏72°方向行走
B.每段直路要短
C.每走完一段直路后沿向右边偏108°方向行走
D.每段直路要长
A
1.如图,∠1,∠2,∠3,∠4是五边形ABCDE的外角,且∠1=∠2=∠3=∠4=75°,则∠AED的度数是( )
A.120° B.115°
C.105° D.100°
A
课堂检测
基础巩固题
2.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是______.?
5
3.一个多边形的每个内角都相等,并且其中一个内角比它相邻的外角大100°,求这个多边形的边数.
解:设每个内角度数为x度,则与它相邻的外角度数为180°-x°,
根据题意可得x-(180-x)=100,解得x=140.
所以每个外角为40°,
所以这个多边形的边数为360°÷40°=9.
答:这个多边形的边数为9.
课堂检测
基础巩固题
4.(1)若一个正多边形的内角是120 °,那么这是正____边形.
(2)已知多边形的每个外角都是45°,则这个多边形是 ______边形.
六
正八
课堂检测
基础巩固题
5.若一个多边形的一个外角与它所有内角和为1 160°,求这个多边形的边数.
解:∵一个多边形的一个外角与它所有内角和为1 160°,
1 160÷180=6……80,
∴n-2=6,解得n=8.
课堂检测
基础巩固题
1.一个n边形的所有内角与它的一个外角的和等于2 000°.求这个外角的度数.
解:2 000÷180=11……20.
故这个外角的度数为20°.
课堂检测
能力提升题
2.某正多边形的一个外角的度数为60°,则这个正多边形的边数为( )
A.6 B.8 C. 10 D. 12
A
如图,AP,CP分别是四边形ABCD的外角∠DAM, ∠DCN的平分线,设∠ABC=α, ∠APC=β,则∠ADC的度数为( )
A.180°-α-β B.α+β
C. α+2β D. 2α+β
C
课堂检测
拓广探索题
多边形的外角及外角和
多边形外角的定义
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
