2020--2021学年沪科版七年级下册数学 第10章 相交线、平行线和平移 达标测试卷(word版含答案)
文档属性
| 名称 | 2020--2021学年沪科版七年级下册数学 第10章 相交线、平行线和平移 达标测试卷(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-05 00:00:00 | ||
图片预览



文档简介
第10章达标测试卷
一、选择题(每题3分,共30分)
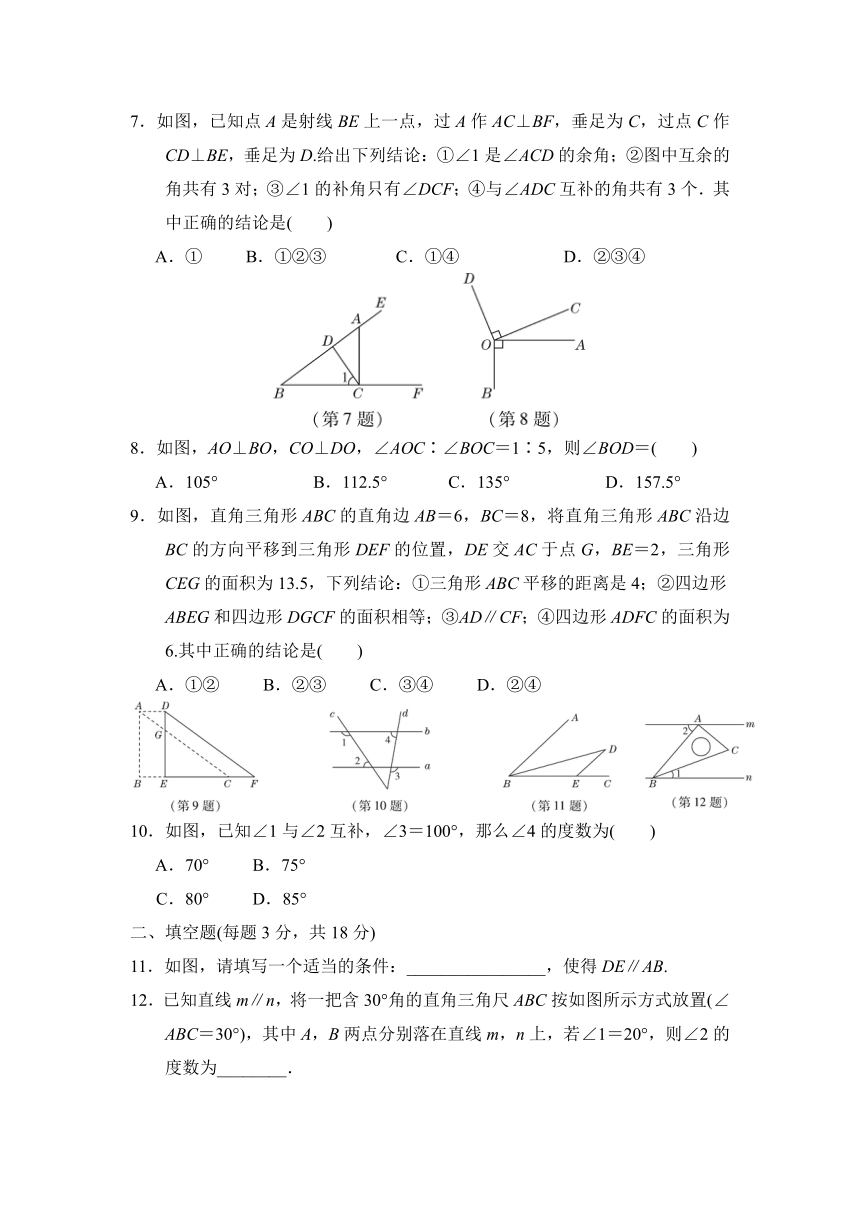
1.如图,∠1的同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
A.50°,40° B.50°,130° C.130°,50° D.50°,50°
3.如图,下列能判定AB∥CD的条件有( )
①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BCD=180°.
A.1个 B.2个 C.3个 D.4个
4.下列各网格中的图形是用其图形中的一部分平移得到的是( )
5.观察如图所示的图形,下列说法正确的是( )
A.线段AB的长必大于点A到直线l的距离
B.图中对顶角共有3对
C.线段AC的长小于线段AB的长,依据是两点之间线段最短
D.线段CD的长是点C到直线AD的距离
6.如图,AB∥DC,点E在BC上,且∠D=∠CED,∠D=74°,则∠B的度数为( )
A.68° B.32° C.22° D.16°
7.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,过点C作CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确的结论是( )
A.① B.①②③ C.①④ D.②③④
8.如图,AO⊥BO,CO⊥DO,∠AOC∶∠BOC=1∶5,则∠BOD=( )
A.105° B.112.5° C.135° D.157.5°
9.如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:①三角形ABC平移的距离是4;②四边形ABEG和四边形DGCF的面积相等;③AD∥CF;④四边形ADFC的面积为6.其中正确的结论是( )
A.①② B.②③ C.③④ D.②④
10.如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )
A.70° B.75°
C.80° D.85°
二、填空题(每题3分,共18分)
11.如图,请填写一个适当的条件:________________,使得DE∥AB.
12.已知直线m∥n,将一把含30°角的直角三角尺ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为________.
13.如图,将一张长方形纸片沿AB折叠,已知∠1=40°,则∠2=________.
14.如图,C为∠AOB的边OA上一点,过C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H.若∠EFD=α,现有以下结论:①CH>CO;②∠COF=α;③CH⊥CD;④∠OCH=2α-90°.其中正确的结论是________.(填序号)
15. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转________°.
16.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为CD延长线上一点,∠BAF=∠EDF.下列结论:①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.其中正确的是______.(只填序号)
三、解答题(21,22题每题10分,其余每题8分,共52分)
17.如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=70°,∠COF=90°.
(1)求∠BOD的度数;
(2)写出图中互余的角;
(3)求∠EOF的度数.
18.如图,点D是∠AOB的平分线OC上的任意一点.
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OB,垂足为点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于________mm(精确到1 mm);
(2)在(1)所画出的图形中,若∠AOB=n°,则∠EDF=________度.(用含n的代数式表示)
19.如图,在三角形ABC中,点E,G分别在BC,AC上,CD⊥AB,EF⊥AB,垂足分别为D,F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的解题过程填写完整.
解:因为EF⊥AB,CD⊥AB(已知),
所以∠BFE=90°,∠BDC=90°( ).
所以∠BFE=∠BDC,所以______∥______( ).
所以∠2+∠______=180°( ).
又因为∠1+∠2=180°(已知),所以∠1=________.
所以BC∥________( ).
所以∠3=________( ).
又因为∠3=105°(已知),所以∠ACB=________.
20.如图,DE⊥AB,垂足为D,EF∥AC,∠A=30°.
(1)求∠DEF的度数.
(2)连接BE,若BE平分∠ABC,EB平分∠DEF,
问EF与BF垂直吗?为什么?
21.如图,∠GDC+∠HBE=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC平行吗?说明理由.
(2)AD与BC有怎样的位置关系?为什么?
(3)过点D作BC的垂线,垂足为M,试说明:∠ABD=2∠CDM.
22.问题情境:如图①,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P在∠APC内部作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图②,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;
(3)联想拓展:在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系;
(4)解决问题:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.试构造平行线解决以下问题.
如图③,已知三角形ABC,试说明:∠A+∠B+∠C=180°.
答案
一、1.C 2.B 3.C 4.C 5.A 6.B 7.C 8.D 9.B
10.C 点拨:如图,因为∠3=100°,
所以∠5=∠3=100°.因为∠1与∠2互补,所以a∥b,所以∠4+∠5=180°,所以∠4=80°.
二、11.∠ABD=∠D(答案不唯一)
12.50°
13.100° 点拨:如图,因为AD∥BC,
所以∠1=∠3=40°.因为长方形纸片沿AB折叠,所以∠4=∠3=40°,
所以∠2=180°-∠3-∠4=180°-40°-40°=100°.
14.②③④ 15.80
16.①②③ 点拨:因为AB⊥BC于点B,DC⊥BC于点C,所以AB∥CD,
所以∠BAD+∠ADC=180°,结论①正确;∠BAF+∠F=180°.
又因为∠BAF=∠EDF,所以∠EDF+∠F=180°,
所以AF∥DE,结论②正确;所以∠ADE=∠DAF,∠CDE=∠F,
因为DE平分∠ADC交BC于点E,
所以∠ADE=∠CDE,所以∠DAF=∠F,结论③正确.故答案为①②③.
三、17.解:(1)因为∠AOC=70°,所以∠BOD=∠AOC=70°.
(2)∠AOC和∠BOF,∠BOD和∠BOF,∠EOF和∠EOD,∠BOE和∠EOF.
(3)因为OE平分∠BOD,∠BOD=70°,
所以∠BOE=35°,因为∠COF=90°,且A、O、B三点在一条直线AB上,
所以∠BOF=180°-70°-90°=20°,所以∠EOF=∠BOF+∠BOE=55°.
18.解:(1)①②③如图所示.
③8 (2)(90-n)
19.垂直的定义;EF;CD;同位角相等,两直线平行;BCD;两直线平行,同旁内角互补;∠BCD;DG;内错角相等,两直线平行;∠ACB;两直线平行,同位角相等;105°
20.解:(1)因为DE⊥AB,∠A=30°,
所以∠AOD=60°.
因为∠COE=∠AOD=60°,EF∥AC,
所以∠DEF+∠COE=180°,所以∠DEF=120°.
(2)EF与BF垂直.理由如下:
由(1)知,∠DEF=120°,
因为EB平分∠DEF,所以∠BEF=∠BED=∠DEF=60°.
又因为DE⊥AB,所以∠DBE=30°,
因为BE平分∠ABC,所以∠EBF=30°,所以∠F=180°-∠EBF-∠BEF=90°,即EF与BF垂直.
21.解:(1)AE∥FC.理由:因为∠GDF+∠GDC=180°,∠GDC+∠HBE=180°,所以∠GDF=∠HBE.
因为∠ABG=∠HBE,所以∠GDF=∠ABG,所以AE∥CF.
(2)AD∥BC.理由:因为AE∥CF,
所以∠ABC+∠C=180°.
因为∠A=∠C,所以∠ABC+∠A=180°,所以AD∥BC.
(3)因为AD∥BC,所以∠ADF=∠C.因为DM⊥BC,
所以∠CDM=90°-∠C=90°-∠ADF.
因为CD∥AB,DA平分∠BDF,
所以∠GDF=∠DBA=180°-2∠ADF,
所以∠ABD=2∠CDM.
22.解:(1)如图①,过P作PE∥AB.
因为AB∥CD,所以PE∥AB∥CD,
所以∠A+∠APE=180°,∠C+∠CPE=180°.因为∠PAB=130°,∠PCD=120°,所以∠APE=50°,∠CPE=60°,
所以∠APC=∠APE+∠CPE=50°+60°=110°.
(2)∠APC=α+β.
理由:如图②,过P作PF∥AB.
因为AB∥CD,所以AB∥PF∥CD,
所以∠APF=∠PAB=α,∠CPF=∠PCD=β,所以∠APC=∠APF+∠CPF=α+β.
(3)当P在BD的延长线上时,
∠APC=α-β;当P在线段OB上时,∠APC=β-α.
(4)如图③,过点A作MN∥BC,
则∠B=∠1,∠C=∠2.
因为∠BAC+∠1+∠2=180°,
所以∠BAC+∠B+∠C=180°.
一、选择题(每题3分,共30分)
1.如图,∠1的同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a,b相交于点O,若∠1=50°,则∠2和∠3的度数分别是( )
A.50°,40° B.50°,130° C.130°,50° D.50°,50°
3.如图,下列能判定AB∥CD的条件有( )
①∠1=∠2;②∠3=∠4;③∠B=∠5;④∠B+∠BCD=180°.
A.1个 B.2个 C.3个 D.4个
4.下列各网格中的图形是用其图形中的一部分平移得到的是( )
5.观察如图所示的图形,下列说法正确的是( )
A.线段AB的长必大于点A到直线l的距离
B.图中对顶角共有3对
C.线段AC的长小于线段AB的长,依据是两点之间线段最短
D.线段CD的长是点C到直线AD的距离
6.如图,AB∥DC,点E在BC上,且∠D=∠CED,∠D=74°,则∠B的度数为( )
A.68° B.32° C.22° D.16°
7.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,过点C作CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确的结论是( )
A.① B.①②③ C.①④ D.②③④
8.如图,AO⊥BO,CO⊥DO,∠AOC∶∠BOC=1∶5,则∠BOD=( )
A.105° B.112.5° C.135° D.157.5°
9.如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:①三角形ABC平移的距离是4;②四边形ABEG和四边形DGCF的面积相等;③AD∥CF;④四边形ADFC的面积为6.其中正确的结论是( )
A.①② B.②③ C.③④ D.②④
10.如图,已知∠1与∠2互补,∠3=100°,那么∠4的度数为( )
A.70° B.75°
C.80° D.85°
二、填空题(每题3分,共18分)
11.如图,请填写一个适当的条件:________________,使得DE∥AB.
12.已知直线m∥n,将一把含30°角的直角三角尺ABC按如图所示方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为________.
13.如图,将一张长方形纸片沿AB折叠,已知∠1=40°,则∠2=________.
14.如图,C为∠AOB的边OA上一点,过C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H.若∠EFD=α,现有以下结论:①CH>CO;②∠COF=α;③CH⊥CD;④∠OCH=2α-90°.其中正确的结论是________.(填序号)
15. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转________°.
16.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为CD延长线上一点,∠BAF=∠EDF.下列结论:①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.其中正确的是______.(只填序号)
三、解答题(21,22题每题10分,其余每题8分,共52分)
17.如图,直线AB,CD相交于点O,OE平分∠BOD,∠AOC=70°,∠COF=90°.
(1)求∠BOD的度数;
(2)写出图中互余的角;
(3)求∠EOF的度数.
18.如图,点D是∠AOB的平分线OC上的任意一点.
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OB,垂足为点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于________mm(精确到1 mm);
(2)在(1)所画出的图形中,若∠AOB=n°,则∠EDF=________度.(用含n的代数式表示)
19.如图,在三角形ABC中,点E,G分别在BC,AC上,CD⊥AB,EF⊥AB,垂足分别为D,F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的解题过程填写完整.
解:因为EF⊥AB,CD⊥AB(已知),
所以∠BFE=90°,∠BDC=90°( ).
所以∠BFE=∠BDC,所以______∥______( ).
所以∠2+∠______=180°( ).
又因为∠1+∠2=180°(已知),所以∠1=________.
所以BC∥________( ).
所以∠3=________( ).
又因为∠3=105°(已知),所以∠ACB=________.
20.如图,DE⊥AB,垂足为D,EF∥AC,∠A=30°.
(1)求∠DEF的度数.
(2)连接BE,若BE平分∠ABC,EB平分∠DEF,
问EF与BF垂直吗?为什么?
21.如图,∠GDC+∠HBE=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC平行吗?说明理由.
(2)AD与BC有怎样的位置关系?为什么?
(3)过点D作BC的垂线,垂足为M,试说明:∠ABD=2∠CDM.
22.问题情境:如图①,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P在∠APC内部作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,请你求出∠APC的度数;
(2)问题迁移:如图②,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;
(3)联想拓展:在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系;
(4)解决问题:我们发现借助构造平行线的方法可以解决许多问题,随着以后的学习你还会发现平行线的许多用途.试构造平行线解决以下问题.
如图③,已知三角形ABC,试说明:∠A+∠B+∠C=180°.
答案
一、1.C 2.B 3.C 4.C 5.A 6.B 7.C 8.D 9.B
10.C 点拨:如图,因为∠3=100°,
所以∠5=∠3=100°.因为∠1与∠2互补,所以a∥b,所以∠4+∠5=180°,所以∠4=80°.
二、11.∠ABD=∠D(答案不唯一)
12.50°
13.100° 点拨:如图,因为AD∥BC,
所以∠1=∠3=40°.因为长方形纸片沿AB折叠,所以∠4=∠3=40°,
所以∠2=180°-∠3-∠4=180°-40°-40°=100°.
14.②③④ 15.80
16.①②③ 点拨:因为AB⊥BC于点B,DC⊥BC于点C,所以AB∥CD,
所以∠BAD+∠ADC=180°,结论①正确;∠BAF+∠F=180°.
又因为∠BAF=∠EDF,所以∠EDF+∠F=180°,
所以AF∥DE,结论②正确;所以∠ADE=∠DAF,∠CDE=∠F,
因为DE平分∠ADC交BC于点E,
所以∠ADE=∠CDE,所以∠DAF=∠F,结论③正确.故答案为①②③.
三、17.解:(1)因为∠AOC=70°,所以∠BOD=∠AOC=70°.
(2)∠AOC和∠BOF,∠BOD和∠BOF,∠EOF和∠EOD,∠BOE和∠EOF.
(3)因为OE平分∠BOD,∠BOD=70°,
所以∠BOE=35°,因为∠COF=90°,且A、O、B三点在一条直线AB上,
所以∠BOF=180°-70°-90°=20°,所以∠EOF=∠BOF+∠BOE=55°.
18.解:(1)①②③如图所示.
③8 (2)(90-n)
19.垂直的定义;EF;CD;同位角相等,两直线平行;BCD;两直线平行,同旁内角互补;∠BCD;DG;内错角相等,两直线平行;∠ACB;两直线平行,同位角相等;105°
20.解:(1)因为DE⊥AB,∠A=30°,
所以∠AOD=60°.
因为∠COE=∠AOD=60°,EF∥AC,
所以∠DEF+∠COE=180°,所以∠DEF=120°.
(2)EF与BF垂直.理由如下:
由(1)知,∠DEF=120°,
因为EB平分∠DEF,所以∠BEF=∠BED=∠DEF=60°.
又因为DE⊥AB,所以∠DBE=30°,
因为BE平分∠ABC,所以∠EBF=30°,所以∠F=180°-∠EBF-∠BEF=90°,即EF与BF垂直.
21.解:(1)AE∥FC.理由:因为∠GDF+∠GDC=180°,∠GDC+∠HBE=180°,所以∠GDF=∠HBE.
因为∠ABG=∠HBE,所以∠GDF=∠ABG,所以AE∥CF.
(2)AD∥BC.理由:因为AE∥CF,
所以∠ABC+∠C=180°.
因为∠A=∠C,所以∠ABC+∠A=180°,所以AD∥BC.
(3)因为AD∥BC,所以∠ADF=∠C.因为DM⊥BC,
所以∠CDM=90°-∠C=90°-∠ADF.
因为CD∥AB,DA平分∠BDF,
所以∠GDF=∠DBA=180°-2∠ADF,
所以∠ABD=2∠CDM.
22.解:(1)如图①,过P作PE∥AB.
因为AB∥CD,所以PE∥AB∥CD,
所以∠A+∠APE=180°,∠C+∠CPE=180°.因为∠PAB=130°,∠PCD=120°,所以∠APE=50°,∠CPE=60°,
所以∠APC=∠APE+∠CPE=50°+60°=110°.
(2)∠APC=α+β.
理由:如图②,过P作PF∥AB.
因为AB∥CD,所以AB∥PF∥CD,
所以∠APF=∠PAB=α,∠CPF=∠PCD=β,所以∠APC=∠APF+∠CPF=α+β.
(3)当P在BD的延长线上时,
∠APC=α-β;当P在线段OB上时,∠APC=β-α.
(4)如图③,过点A作MN∥BC,
则∠B=∠1,∠C=∠2.
因为∠BAC+∠1+∠2=180°,
所以∠BAC+∠B+∠C=180°.
