2020-2021学年安徽省池州市东至高二(下)开年考数学试卷(文科) (Word解析版)
文档属性
| 名称 | 2020-2021学年安徽省池州市东至高二(下)开年考数学试卷(文科) (Word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 14:56:54 | ||
图片预览




文档简介
2020-2021学年安徽省池州市东至高二(下)开年考(文科)数学试卷
一、选择题(共12小题).
1.已知a,b∈R,下列选项中,使ab>0成立的一个充分不必要条件是( )
A.a>0或b>0 B.a>10且b>2
C.a,b同号且不为0 D.a+b>0或ab>0
2.若双曲线的焦距为8,则双曲线C的虚轴长为( )
A.2 B.3 C.4 D.6
3.已知曲线y=axb在点(﹣1,a)处的切线方程为8x﹣y+6=0,则( )
A.a=2,b=4 B.a=﹣2,b=4 C.a=8,b=1 D.a=8,b=﹣1
4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m?α,α⊥β,则m⊥β
B.若α∩β=m,β∩γ=n,m∥n,则α∥β
C.若α⊥β,β⊥γ,则α⊥γ
D.若m⊥α,m∥β,则α⊥β
5.直线7x+y﹣2=0与圆C:(x﹣1)2+y2=r2(r>0)相交于A,B两点,若△ABC为直角三角形,则r=( )
A.1 B. C. D.2
6.过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于A,B两点,|AB|=6,弦AB中点P的横坐标xP=2,则该抛物线的方程为( )
A.y2=2x B.y2=4x C.y2=6x D.y2=8x
7.已知函数为f(x)的导函数,若f'(a)=f(a),则a=( )
A.0 B.﹣1 C.2 D.0或2
8.若直线y=x+b与曲线有两个不同的公共点,则实数b的取值范围是( )
A. B. C. D.
9.四面体A﹣BCD中,DC⊥面ABC,AB=BC=3,∠ABC=120°,DC=8,则四面体A﹣BCD外接球的表面积为( )
A.100π B.50π C.25π D.91π
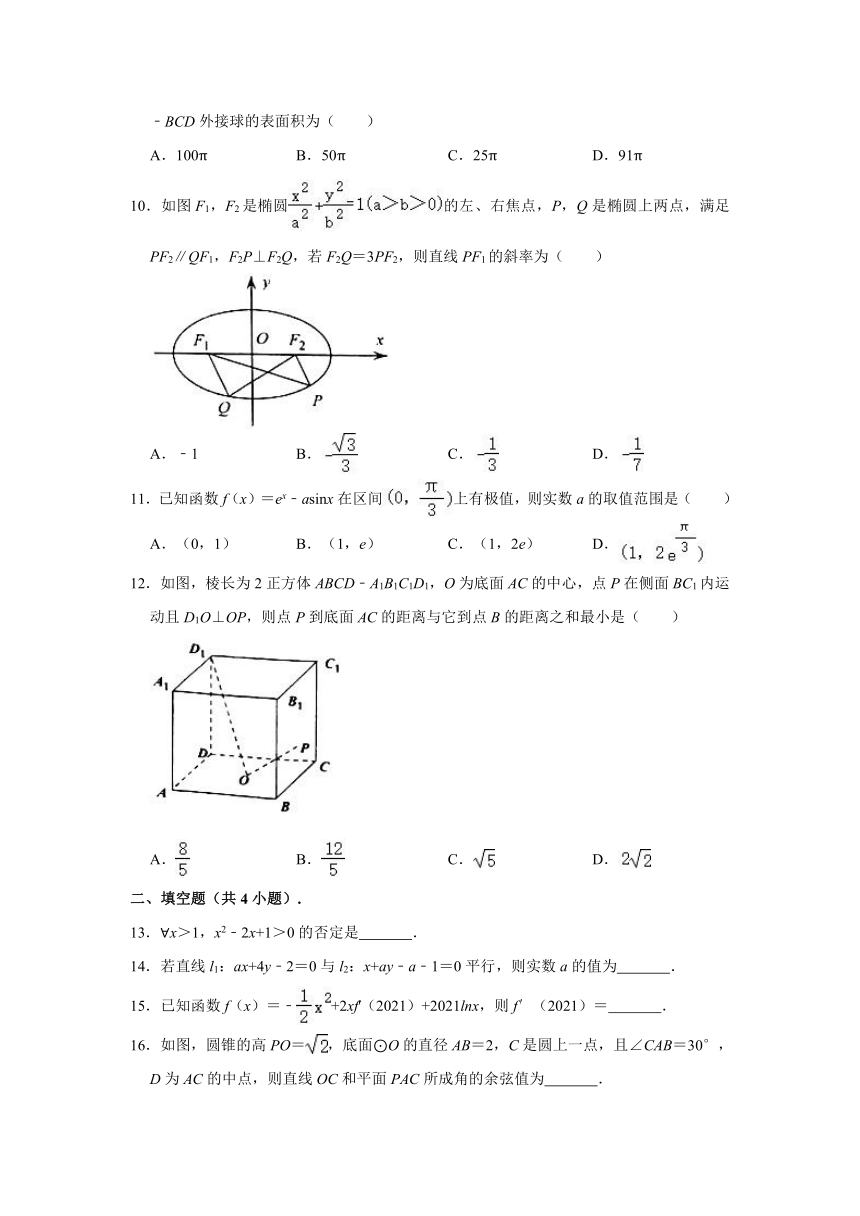
10.如图F1,F2是椭圆的左、右焦点,P,Q是椭圆上两点,满足PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,则直线PF1的斜率为( )
A.﹣1 B. C. D.
11.已知函数f(x)=ex﹣asinx在区间上有极值,则实数a的取值范围是( )
A.(0,1) B.(1,e) C.(1,2e) D.
12.如图,棱长为2正方体ABCD﹣A1B1C1D1,O为底面AC的中心,点P在侧面BC1内运动且D1O⊥OP,则点P到底面AC的距离与它到点B的距离之和最小是( )
A. B. C. D.
二、填空题(共4小题).
13.?x>1,x2﹣2x+1>0的否定是 .
14.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为 .
15.已知函数f(x)=﹣+2xf'(2021)+2021lnx,则f′(2021)= .
16.如图,圆锥的高PO=,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的余弦值为 .
三、解答题:共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知命题p:?x∈[1,2],3x2﹣mx+2<0;命题q:函数在区间(0,1)上单调递减.其中m为常数.(1)若p为真命题,求m的取值范围;
(2)若(¬p)∧q为真命题,求m的取值范围.
18.已知直线l经过点P(﹣2,4).
(Ⅰ)若原点到直线l的距离为2,求直线l的方程;
(Ⅱ)若直线l被两条相交直线l1:2x﹣y﹣2=0和l2:x+y+3=0所截得的线段恰被点P平分,求直线l的方程.
19.如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过A、C两点,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
(1)求证:平面EFP⊥平面BCE;
(2)求几何体ADG﹣BCE的体积.
20.《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书本记载了一种名为“刍甍”的五面体(如图1).其中四边形ABCD为矩形,EF∥AB,△EAD和△FBC是三角形,“刍甍”字面意思为茅草屋顶.图2是一栋农村别墅,为全新的混凝土结构.它由上部屋顶和下部主体两部分组成.如图3,屋顶五面体为“刍甍”,其中前后两坡屋面ABEF和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形,点F在平面ABCD和BC上射影分别为H,M,已知HM=5米,BC=10米,梯形ABEF的面积是△FBC面积的2.2倍.设.
(1)求屋顶面积S关于θ的函数关系式;
(2)已知上部屋顶造价由屋顶面积确定,造价为600元/平方米,下部主体造价由高度确定,造价为9600元/米.现欲造一栋上、下总高度为6米的别墅,试问:当θ为何值时,总造价最低?
21.已知椭圆的离心率为,点F1,F2分别为其左、右焦点,点A,B分别为其左、右顶点,点Q为椭圆上不与A,B重合的动点,且△QAF1面积的最大值为.
(1)求椭圆C的方程;
(2)分别过点A,B作直线l1⊥AQ于点A,l2⊥BQ于点B,设l1与l2相交于点P,求点P的轨迹方程.
22.设函数.
(1)求f(x)的单调区间;
(2)求证:当x∈[1,ea]时,.
参考答案
一、选择题(共12小题).
1.已知a,b∈R,下列选项中,使ab>0成立的一个充分不必要条件是( )
A.a>0或b>0 B.a>10且b>2
C.a,b同号且不为0 D.a+b>0或ab>0
解:对于A:a>0或b>0不能够推出ab>0,故a>0或b>0不是ab>0的充分条件,故A错误,
对于B:a>10且b>2,能够推出ab>0,ab>0不能够推出a>10且b>2,故a>10且b>2,是ab>0的充分不必要条件,故B正确,
对于C:a,b同号且不为0?ab>0,故a,b同号且不为0是ab>0的充要条件,故C错误,
对于D:a+b>0或ab>0与ab>0互相推不出,故a+b>0或ab>0与ab>0是既不充分也不必要条件,故D错误.
故选:B.
2.若双曲线的焦距为8,则双曲线C的虚轴长为( )
A.2 B.3 C.4 D.6
解:依题意双曲线的焦距为8,
12+n=16,故n=4,则双曲线C的虚轴长为4,
故选:C.
3.已知曲线y=axb在点(﹣1,a)处的切线方程为8x﹣y+6=0,则( )
A.a=2,b=4 B.a=﹣2,b=4 C.a=8,b=1 D.a=8,b=﹣1
解:将(﹣1,a)代入8x﹣y+6=0,
得a=﹣2,
又因为y'=abxb﹣1,
所以b(﹣1)b﹣1=﹣4,b=4.
故选:B.
4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m?α,α⊥β,则m⊥β
B.若α∩β=m,β∩γ=n,m∥n,则α∥β
C.若α⊥β,β⊥γ,则α⊥γ
D.若m⊥α,m∥β,则α⊥β
解:由m,n是两条不同的直线,α,β,γ是三个不同的平面,知:
在A中,若m?α,α⊥β,则m与β相交、平行或m?β,故A错误;
在B中,若α∩β=m,β∩γ=n,m∥n,则α与β相交或平行,故B错误;
在C中,若α⊥β,β⊥γ,则α与γ相交或平行,故C错误;
在D中,若m⊥α,m∥β,则由面面垂直的判定定理得α⊥β,故D正确.
故选:D.
5.直线7x+y﹣2=0与圆C:(x﹣1)2+y2=r2(r>0)相交于A,B两点,若△ABC为直角三角形,则r=( )
A.1 B. C. D.2
解:圆C的圆心为(1,0).
圆心C到直线7x+y﹣2=0的距离为为直角三角形,
则一定为等腰直角三角形且C为直角,
所以.
故选:A.
6.过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于A,B两点,|AB|=6,弦AB中点P的横坐标xP=2,则该抛物线的方程为( )
A.y2=2x B.y2=4x C.y2=6x D.y2=8x
解:设A(x1,y1),B(x2,y2),由抛物线定义知:x1+x2+p=6,
又,即p=2,
故抛物线方程为y2=4x.
故选:B.
7.已知函数为f(x)的导函数,若f'(a)=f(a),则a=( )
A.0 B.﹣1 C.2 D.0或2
解:因为f'(x)=ex﹣ex,根据条件得,解得a=0或2.
故选:D.
8.若直线y=x+b与曲线有两个不同的公共点,则实数b的取值范围是( )
A. B. C. D.
解:曲线方程变形为x2+(y﹣2)2=4(y≥2),表示圆心C为(0,2),半径为2的上半圆,
据题意画出图形,如图所示:
当直线y=x+b过点(0,4)时,可得b=4,满足直线y=x+b与曲线y=2+有两个不同的公共点.
当直线y=x+b和半圆相切时,由2=,解得b=2+或b=2﹣2(舍去),
故直线y=x+b与曲线y=2+有两个不同的公共点时,实数b的取值范围为[4,2+2),
故选:C.
9.四面体A﹣BCD中,DC⊥面ABC,AB=BC=3,∠ABC=120°,DC=8,则四面体A﹣BCD外接球的表面积为( )
A.100π B.50π C.25π D.91π
解:设△ABC外接圆的圆心为O1,四面体A﹣BCD外接球的球心为O,半径为R,
连接O1C,OO1,OC,
由正弦定理可得,即,,,
即四面体A﹣BCD外接球的表面积为S=4π×52=100π,
故选:A.
10.如图F1,F2是椭圆的左、右焦点,P,Q是椭圆上两点,满足PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,则直线PF1的斜率为( )
A.﹣1 B. C. D.
解:由题意PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,取Q点关于原点O的对称点M,
则F1M=F2Q,F1Q=F2M,所以四边形F1QF2M为矩形,得到M,O,F2,共线,
设F2P=x,则F2Q=3x,
由椭圆定义可得F1P=2a﹣x,F2M=2a﹣3x,MP=2a+2x,
∵∠F1MF2=90°,则(2a﹣2x)2+4x2=(2a﹣x)2,解得x=,
∴,F2Q=3x=a,F1Q=a,
∴∠F1QF2=∠QF2P=∠PF2x=45°,
过P作x轴的垂线,垂足为N,
则PN=,F1N=,
所以k=﹣=﹣.
故选:D.
11.已知函数f(x)=ex﹣asinx在区间上有极值,则实数a的取值范围是( )
A.(0,1) B.(1,e) C.(1,2e) D.
解:f(x)=ex﹣asinx,x∈,
则f′(x)=ex﹣acosx,
由题意得ex﹣acosx=0在(0,)上有解,
即a=在(0,)上有解,
记g(x)=,x∈(0,),
则g′(x)=,
当x∈(0,)时,g′(x)>0,g(x)递增,
而g(0)=1,g()=2,
故1<a<2,
故选:D.
12.如图,棱长为2正方体ABCD﹣A1B1C1D1,O为底面AC的中心,点P在侧面BC1内运动且D1O⊥OP,则点P到底面AC的距离与它到点B的距离之和最小是( )
A. B. C. D.
解:如图,
由正方体性质知,当P位于C点时,D1O⊥OC,
当P位于BB1 的中点P1 时,由已知得,DD1=2,DO=BO=,
BP1=B1P1=1,B1D1=2 ,
求得OD1==,OP1==,D1P1==3.
∴OD12+OP12=D1P12,得OD1⊥OP1.
又OP1∩OC=O,OP1?平面OP1 C,OC?平面OP1 C,
∴D1O⊥平面OP1 C,得到P的轨迹在线段P1C上.
过B作关于CP1的对称点B',过P作PH⊥BC于H,
当B',P,H三点共线时,点P到底面AC的距离与它到点B的距离之和取得最小值.
在直角三角形P1BC中,BC=2,P1B=1,P1C==,
BB'=,所以B'H=BB'sin∠HBB'=×=,
故选:A.
二、填空题:本大题共4小题
13.?x>1,x2﹣2x+1>0的否定是 ?x>1,x2﹣2x+1≤0 .
解:全称命题?x>1,x2﹣2x+1>0,
由全称命题的否定是特称命题得?x>1,x2﹣2x+1>0的否定是:?x>1,x2﹣2x+1≤0.
故答案为:?x>1,x2﹣2x+1≤0.
14.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为 2 .
解:因为直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,
所以,解得a=2.
故答案为:2.
15.已知函数f(x)=﹣+2xf'(2021)+2021lnx,则f′(2021)= 2020 .
解:∵,
∴,
∴f'(2021)=﹣2021+2f'(2021)+1,
∴f'(2021)=2020.
故答案为:2020.
16.如图,圆锥的高PO=,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的余弦值为 .
解:设点O到平面PAC的距离为d,设直线OC和平面PAC所成角为α,
则由等体积法有:VO﹣PAC=VP﹣OAC,
即S△PAC?d=?PO?S△OAC,
在△AOC中,求得AC=,
在△POD中,求得PD=,
∴d==,
∴sin α==,于是cos α==,
故答案为.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知命题p:?x∈[1,2],3x2﹣mx+2<0;命题q:函数在区间(0,1)上单调递减.其中m为常数.(1)若p为真命题,求m的取值范围;
(2)若(¬p)∧q为真命题,求m的取值范围.
解:(1)令f(x)=3x2﹣mx+2,其图象是开口向上的抛物线,
要使p为真命题,则f(1)<0且f(2)<0,
即
所以m>7,
所以m的取值范围是(7,+∞).
(2)若(¬p)∧q为真命题,则p为假命题,q为真命题
由(1)知,p为假命题等价于m≤7.
对于命题q,当m≤0时,函数在(0,1)上单调递增,不满足条件;
当m>0时,函数在上单调递减,在上单调递增,
要使在(0,1)上单调递减,则,即m≥1,
综上所述,若(¬p)∧q为真命题,m的取值范围是[1,7].
18.已知直线l经过点P(﹣2,4).
(Ⅰ)若原点到直线l的距离为2,求直线l的方程;
(Ⅱ)若直线l被两条相交直线l1:2x﹣y﹣2=0和l2:x+y+3=0所截得的线段恰被点P平分,求直线l的方程.
解:(Ⅰ)①直线l的斜率不存在时,直线方程为x=﹣2,符合条件.
②直线l的斜率存在时,设直线方程为y﹣4=k(x+2),
由原点到直线l的距离为2得,解,
故直线l的方程为,
即3x+4y﹣10=0,
综上,所求直线l的方程为x=﹣2或3x+4y﹣10=0.
(Ⅱ)设直线l夹在直线l1,l2之间的线段为AB(A在l1上,B在l2上),
A,B的坐标分别设为(x1,y1),(x2,y2)
因为AB被点P平分,所以x1+x2=﹣4,y1+y2=8,即x2=﹣4﹣x1,y2=8﹣y1.
由于A在l1上,B在l2上,即,
解得x1=3,y1=4,即A的坐标是(3,4),
又直线过点P(﹣2,4),
故直线l的方程是y=4.
19.如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过A、C两点,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
(1)求证:平面EFP⊥平面BCE;
(2)求几何体ADG﹣BCE的体积.
【解答】(Ⅰ)证明:∵点E在平面ABCD内的射影恰为A,
∴AE⊥平面ABCD,
又AE?平面ABEG,∴平面ABCD⊥平面ABEG,
又以BD为直径的圆经过A,C,AD=AB,∴ABCD为正方形,
又平面ABCD∩平面ABEG=AB,∴BC⊥平面ABEG,
∵EF?平面ABEG,∴EF⊥BC,
又AB=AE=GE,∴∠ABE=∠AEB=,
又AG的中点为F,∴∠AEF=.
∵∠AEF+∠AEB=,∴EF⊥BE.
又BE?平面BCE,BC?平面BCE,BC∩BE=B,
∴EF⊥平面BCE,
又EF?平面EFP,∴平面EFP⊥平面BCE;
(Ⅱ)解:连接DE,由(Ⅰ)知,AE⊥平面ABCD,
∴AE⊥AD,又AB⊥AD,AE∩AD=A,
∴AB⊥平面ADE,又AB∥GE,∴GE⊥平面ADE.
∴VADC﹣BCE=
=.
∴几何体ADC﹣BCE的体积为4.
20.《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书本记载了一种名为“刍甍”的五面体(如图1).其中四边形ABCD为矩形,EF∥AB,△EAD和△FBC是三角形,“刍甍”字面意思为茅草屋顶.图2是一栋农村别墅,为全新的混凝土结构.它由上部屋顶和下部主体两部分组成.如图3,屋顶五面体为“刍甍”,其中前后两坡屋面ABEF和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形,点F在平面ABCD和BC上射影分别为H,M,已知HM=5米,BC=10米,梯形ABEF的面积是△FBC面积的2.2倍.设.
(1)求屋顶面积S关于θ的函数关系式;
(2)已知上部屋顶造价由屋顶面积确定,造价为600元/平方米,下部主体造价由高度确定,造价为9600元/米.现欲造一栋上、下总高度为6米的别墅,试问:当θ为何值时,总造价最低?
解:(1)在Rt△FHM中,FM==,
∴S△FBC=FM?BC=×10=,
∵梯形ABEF的面积是△FBC面积的2.2倍,即S梯形ABEF=2.2S△FBC,
∴屋顶面积S=2(S△FBC+S梯形ABEF)=2×3.2S△FBC=2×3.2×=,.
(2)在Rt△FHM中,FH=HM?tanθ=5tanθ,
∴下部主体的高度为6﹣5tanθ,
∴总造价y=×600+(6﹣5tanθ)×9600=9600×(+6﹣)=9600×(+6),
设f(θ)=,要使总造价最低,则f(θ)最小,
f'(θ)==,
令f'(θ)=0,则sinθ=,
∵,∴θ=,
当θ∈(0,)时,f'(θ)<0,f(θ)单调递减,当θ∈(,)时,f'(θ)>0,f(θ)单调递增,
∴当时,f(θ)取得最小值,
故当时,总造价最低.
21.已知椭圆的离心率为,点F1,F2分别为其左、右焦点,点A,B分别为其左、右顶点,点Q为椭圆上不与A,B重合的动点,且△QAF1面积的最大值为.
(1)求椭圆C的方程;
(2)分别过点A,B作直线l1⊥AQ于点A,l2⊥BQ于点B,设l1与l2相交于点P,求点P的轨迹方程.
解:(1)由题意得,即a=2c.
又,点Q为椭圆上的动点.
故|yQ|≤b,则的最大值为
即(a﹣c)2(a2﹣c2)=3,代入a=2c得c=1,故a=2,,
即椭圆方程为.
(2)设Q(x0,y0),P(x,y),则.①
由题意得:,,,,
则kAQ?kAP=﹣1,kBQ?kBP=﹣1.
且kAQ?kBQ=,代入①得,
又kAQ?kAP?kBQ?kBP=1,
所以,
即,整理得.
故为所求轨迹方程.
22.设函数.
(1)求f(x)的单调区间;
(2)求证:当x∈[1,ea]时,.
解:(1)由题意得,
令f'(x)=0,得,由f'(x)>0,得,由f'(x)<0,得,
所以f(x)的单调递增区间为,单调递减区间为;
(2)证明:若,即0<a≤2,由(1)知f(x)在[1,ea]上单调递增,
所以f(x)的最大值是f(ea)=ea﹣,若,即a>2,
设g(a)=ea﹣a,则当a>2时,g'(a)=ea﹣1>0,
所以g(a)>g(2)=e2﹣2>0,所以,从而,
结合(1)可知,f(x)在上单调递减,在上单调递增,
下面比较和f(1)=1的大小
设,当a>2时,h'(a)=ea﹣a>0,
所以h(a)>h(2)=e2﹣2>1,即f(ea)>f(1)
所以当x∈[1,ea]时,.
一、选择题(共12小题).
1.已知a,b∈R,下列选项中,使ab>0成立的一个充分不必要条件是( )
A.a>0或b>0 B.a>10且b>2
C.a,b同号且不为0 D.a+b>0或ab>0
2.若双曲线的焦距为8,则双曲线C的虚轴长为( )
A.2 B.3 C.4 D.6
3.已知曲线y=axb在点(﹣1,a)处的切线方程为8x﹣y+6=0,则( )
A.a=2,b=4 B.a=﹣2,b=4 C.a=8,b=1 D.a=8,b=﹣1
4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m?α,α⊥β,则m⊥β
B.若α∩β=m,β∩γ=n,m∥n,则α∥β
C.若α⊥β,β⊥γ,则α⊥γ
D.若m⊥α,m∥β,则α⊥β
5.直线7x+y﹣2=0与圆C:(x﹣1)2+y2=r2(r>0)相交于A,B两点,若△ABC为直角三角形,则r=( )
A.1 B. C. D.2
6.过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于A,B两点,|AB|=6,弦AB中点P的横坐标xP=2,则该抛物线的方程为( )
A.y2=2x B.y2=4x C.y2=6x D.y2=8x
7.已知函数为f(x)的导函数,若f'(a)=f(a),则a=( )
A.0 B.﹣1 C.2 D.0或2
8.若直线y=x+b与曲线有两个不同的公共点,则实数b的取值范围是( )
A. B. C. D.
9.四面体A﹣BCD中,DC⊥面ABC,AB=BC=3,∠ABC=120°,DC=8,则四面体A﹣BCD外接球的表面积为( )
A.100π B.50π C.25π D.91π
10.如图F1,F2是椭圆的左、右焦点,P,Q是椭圆上两点,满足PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,则直线PF1的斜率为( )
A.﹣1 B. C. D.
11.已知函数f(x)=ex﹣asinx在区间上有极值,则实数a的取值范围是( )
A.(0,1) B.(1,e) C.(1,2e) D.
12.如图,棱长为2正方体ABCD﹣A1B1C1D1,O为底面AC的中心,点P在侧面BC1内运动且D1O⊥OP,则点P到底面AC的距离与它到点B的距离之和最小是( )
A. B. C. D.
二、填空题(共4小题).
13.?x>1,x2﹣2x+1>0的否定是 .
14.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为 .
15.已知函数f(x)=﹣+2xf'(2021)+2021lnx,则f′(2021)= .
16.如图,圆锥的高PO=,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的余弦值为 .
三、解答题:共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知命题p:?x∈[1,2],3x2﹣mx+2<0;命题q:函数在区间(0,1)上单调递减.其中m为常数.(1)若p为真命题,求m的取值范围;
(2)若(¬p)∧q为真命题,求m的取值范围.
18.已知直线l经过点P(﹣2,4).
(Ⅰ)若原点到直线l的距离为2,求直线l的方程;
(Ⅱ)若直线l被两条相交直线l1:2x﹣y﹣2=0和l2:x+y+3=0所截得的线段恰被点P平分,求直线l的方程.
19.如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过A、C两点,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
(1)求证:平面EFP⊥平面BCE;
(2)求几何体ADG﹣BCE的体积.
20.《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书本记载了一种名为“刍甍”的五面体(如图1).其中四边形ABCD为矩形,EF∥AB,△EAD和△FBC是三角形,“刍甍”字面意思为茅草屋顶.图2是一栋农村别墅,为全新的混凝土结构.它由上部屋顶和下部主体两部分组成.如图3,屋顶五面体为“刍甍”,其中前后两坡屋面ABEF和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形,点F在平面ABCD和BC上射影分别为H,M,已知HM=5米,BC=10米,梯形ABEF的面积是△FBC面积的2.2倍.设.
(1)求屋顶面积S关于θ的函数关系式;
(2)已知上部屋顶造价由屋顶面积确定,造价为600元/平方米,下部主体造价由高度确定,造价为9600元/米.现欲造一栋上、下总高度为6米的别墅,试问:当θ为何值时,总造价最低?
21.已知椭圆的离心率为,点F1,F2分别为其左、右焦点,点A,B分别为其左、右顶点,点Q为椭圆上不与A,B重合的动点,且△QAF1面积的最大值为.
(1)求椭圆C的方程;
(2)分别过点A,B作直线l1⊥AQ于点A,l2⊥BQ于点B,设l1与l2相交于点P,求点P的轨迹方程.
22.设函数.
(1)求f(x)的单调区间;
(2)求证:当x∈[1,ea]时,.
参考答案
一、选择题(共12小题).
1.已知a,b∈R,下列选项中,使ab>0成立的一个充分不必要条件是( )
A.a>0或b>0 B.a>10且b>2
C.a,b同号且不为0 D.a+b>0或ab>0
解:对于A:a>0或b>0不能够推出ab>0,故a>0或b>0不是ab>0的充分条件,故A错误,
对于B:a>10且b>2,能够推出ab>0,ab>0不能够推出a>10且b>2,故a>10且b>2,是ab>0的充分不必要条件,故B正确,
对于C:a,b同号且不为0?ab>0,故a,b同号且不为0是ab>0的充要条件,故C错误,
对于D:a+b>0或ab>0与ab>0互相推不出,故a+b>0或ab>0与ab>0是既不充分也不必要条件,故D错误.
故选:B.
2.若双曲线的焦距为8,则双曲线C的虚轴长为( )
A.2 B.3 C.4 D.6
解:依题意双曲线的焦距为8,
12+n=16,故n=4,则双曲线C的虚轴长为4,
故选:C.
3.已知曲线y=axb在点(﹣1,a)处的切线方程为8x﹣y+6=0,则( )
A.a=2,b=4 B.a=﹣2,b=4 C.a=8,b=1 D.a=8,b=﹣1
解:将(﹣1,a)代入8x﹣y+6=0,
得a=﹣2,
又因为y'=abxb﹣1,
所以b(﹣1)b﹣1=﹣4,b=4.
故选:B.
4.若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m?α,α⊥β,则m⊥β
B.若α∩β=m,β∩γ=n,m∥n,则α∥β
C.若α⊥β,β⊥γ,则α⊥γ
D.若m⊥α,m∥β,则α⊥β
解:由m,n是两条不同的直线,α,β,γ是三个不同的平面,知:
在A中,若m?α,α⊥β,则m与β相交、平行或m?β,故A错误;
在B中,若α∩β=m,β∩γ=n,m∥n,则α与β相交或平行,故B错误;
在C中,若α⊥β,β⊥γ,则α与γ相交或平行,故C错误;
在D中,若m⊥α,m∥β,则由面面垂直的判定定理得α⊥β,故D正确.
故选:D.
5.直线7x+y﹣2=0与圆C:(x﹣1)2+y2=r2(r>0)相交于A,B两点,若△ABC为直角三角形,则r=( )
A.1 B. C. D.2
解:圆C的圆心为(1,0).
圆心C到直线7x+y﹣2=0的距离为为直角三角形,
则一定为等腰直角三角形且C为直角,
所以.
故选:A.
6.过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于A,B两点,|AB|=6,弦AB中点P的横坐标xP=2,则该抛物线的方程为( )
A.y2=2x B.y2=4x C.y2=6x D.y2=8x
解:设A(x1,y1),B(x2,y2),由抛物线定义知:x1+x2+p=6,
又,即p=2,
故抛物线方程为y2=4x.
故选:B.
7.已知函数为f(x)的导函数,若f'(a)=f(a),则a=( )
A.0 B.﹣1 C.2 D.0或2
解:因为f'(x)=ex﹣ex,根据条件得,解得a=0或2.
故选:D.
8.若直线y=x+b与曲线有两个不同的公共点,则实数b的取值范围是( )
A. B. C. D.
解:曲线方程变形为x2+(y﹣2)2=4(y≥2),表示圆心C为(0,2),半径为2的上半圆,
据题意画出图形,如图所示:
当直线y=x+b过点(0,4)时,可得b=4,满足直线y=x+b与曲线y=2+有两个不同的公共点.
当直线y=x+b和半圆相切时,由2=,解得b=2+或b=2﹣2(舍去),
故直线y=x+b与曲线y=2+有两个不同的公共点时,实数b的取值范围为[4,2+2),
故选:C.
9.四面体A﹣BCD中,DC⊥面ABC,AB=BC=3,∠ABC=120°,DC=8,则四面体A﹣BCD外接球的表面积为( )
A.100π B.50π C.25π D.91π
解:设△ABC外接圆的圆心为O1,四面体A﹣BCD外接球的球心为O,半径为R,
连接O1C,OO1,OC,
由正弦定理可得,即,,,
即四面体A﹣BCD外接球的表面积为S=4π×52=100π,
故选:A.
10.如图F1,F2是椭圆的左、右焦点,P,Q是椭圆上两点,满足PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,则直线PF1的斜率为( )
A.﹣1 B. C. D.
解:由题意PF2∥QF1,F2P⊥F2Q,若F2Q=3PF2,取Q点关于原点O的对称点M,
则F1M=F2Q,F1Q=F2M,所以四边形F1QF2M为矩形,得到M,O,F2,共线,
设F2P=x,则F2Q=3x,
由椭圆定义可得F1P=2a﹣x,F2M=2a﹣3x,MP=2a+2x,
∵∠F1MF2=90°,则(2a﹣2x)2+4x2=(2a﹣x)2,解得x=,
∴,F2Q=3x=a,F1Q=a,
∴∠F1QF2=∠QF2P=∠PF2x=45°,
过P作x轴的垂线,垂足为N,
则PN=,F1N=,
所以k=﹣=﹣.
故选:D.
11.已知函数f(x)=ex﹣asinx在区间上有极值,则实数a的取值范围是( )
A.(0,1) B.(1,e) C.(1,2e) D.
解:f(x)=ex﹣asinx,x∈,
则f′(x)=ex﹣acosx,
由题意得ex﹣acosx=0在(0,)上有解,
即a=在(0,)上有解,
记g(x)=,x∈(0,),
则g′(x)=,
当x∈(0,)时,g′(x)>0,g(x)递增,
而g(0)=1,g()=2,
故1<a<2,
故选:D.
12.如图,棱长为2正方体ABCD﹣A1B1C1D1,O为底面AC的中心,点P在侧面BC1内运动且D1O⊥OP,则点P到底面AC的距离与它到点B的距离之和最小是( )
A. B. C. D.
解:如图,
由正方体性质知,当P位于C点时,D1O⊥OC,
当P位于BB1 的中点P1 时,由已知得,DD1=2,DO=BO=,
BP1=B1P1=1,B1D1=2 ,
求得OD1==,OP1==,D1P1==3.
∴OD12+OP12=D1P12,得OD1⊥OP1.
又OP1∩OC=O,OP1?平面OP1 C,OC?平面OP1 C,
∴D1O⊥平面OP1 C,得到P的轨迹在线段P1C上.
过B作关于CP1的对称点B',过P作PH⊥BC于H,
当B',P,H三点共线时,点P到底面AC的距离与它到点B的距离之和取得最小值.
在直角三角形P1BC中,BC=2,P1B=1,P1C==,
BB'=,所以B'H=BB'sin∠HBB'=×=,
故选:A.
二、填空题:本大题共4小题
13.?x>1,x2﹣2x+1>0的否定是 ?x>1,x2﹣2x+1≤0 .
解:全称命题?x>1,x2﹣2x+1>0,
由全称命题的否定是特称命题得?x>1,x2﹣2x+1>0的否定是:?x>1,x2﹣2x+1≤0.
故答案为:?x>1,x2﹣2x+1≤0.
14.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为 2 .
解:因为直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,
所以,解得a=2.
故答案为:2.
15.已知函数f(x)=﹣+2xf'(2021)+2021lnx,则f′(2021)= 2020 .
解:∵,
∴,
∴f'(2021)=﹣2021+2f'(2021)+1,
∴f'(2021)=2020.
故答案为:2020.
16.如图,圆锥的高PO=,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的余弦值为 .
解:设点O到平面PAC的距离为d,设直线OC和平面PAC所成角为α,
则由等体积法有:VO﹣PAC=VP﹣OAC,
即S△PAC?d=?PO?S△OAC,
在△AOC中,求得AC=,
在△POD中,求得PD=,
∴d==,
∴sin α==,于是cos α==,
故答案为.
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17.已知命题p:?x∈[1,2],3x2﹣mx+2<0;命题q:函数在区间(0,1)上单调递减.其中m为常数.(1)若p为真命题,求m的取值范围;
(2)若(¬p)∧q为真命题,求m的取值范围.
解:(1)令f(x)=3x2﹣mx+2,其图象是开口向上的抛物线,
要使p为真命题,则f(1)<0且f(2)<0,
即
所以m>7,
所以m的取值范围是(7,+∞).
(2)若(¬p)∧q为真命题,则p为假命题,q为真命题
由(1)知,p为假命题等价于m≤7.
对于命题q,当m≤0时,函数在(0,1)上单调递增,不满足条件;
当m>0时,函数在上单调递减,在上单调递增,
要使在(0,1)上单调递减,则,即m≥1,
综上所述,若(¬p)∧q为真命题,m的取值范围是[1,7].
18.已知直线l经过点P(﹣2,4).
(Ⅰ)若原点到直线l的距离为2,求直线l的方程;
(Ⅱ)若直线l被两条相交直线l1:2x﹣y﹣2=0和l2:x+y+3=0所截得的线段恰被点P平分,求直线l的方程.
解:(Ⅰ)①直线l的斜率不存在时,直线方程为x=﹣2,符合条件.
②直线l的斜率存在时,设直线方程为y﹣4=k(x+2),
由原点到直线l的距离为2得,解,
故直线l的方程为,
即3x+4y﹣10=0,
综上,所求直线l的方程为x=﹣2或3x+4y﹣10=0.
(Ⅱ)设直线l夹在直线l1,l2之间的线段为AB(A在l1上,B在l2上),
A,B的坐标分别设为(x1,y1),(x2,y2)
因为AB被点P平分,所以x1+x2=﹣4,y1+y2=8,即x2=﹣4﹣x1,y2=8﹣y1.
由于A在l1上,B在l2上,即,
解得x1=3,y1=4,即A的坐标是(3,4),
又直线过点P(﹣2,4),
故直线l的方程是y=4.
19.如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过A、C两点,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
(1)求证:平面EFP⊥平面BCE;
(2)求几何体ADG﹣BCE的体积.
【解答】(Ⅰ)证明:∵点E在平面ABCD内的射影恰为A,
∴AE⊥平面ABCD,
又AE?平面ABEG,∴平面ABCD⊥平面ABEG,
又以BD为直径的圆经过A,C,AD=AB,∴ABCD为正方形,
又平面ABCD∩平面ABEG=AB,∴BC⊥平面ABEG,
∵EF?平面ABEG,∴EF⊥BC,
又AB=AE=GE,∴∠ABE=∠AEB=,
又AG的中点为F,∴∠AEF=.
∵∠AEF+∠AEB=,∴EF⊥BE.
又BE?平面BCE,BC?平面BCE,BC∩BE=B,
∴EF⊥平面BCE,
又EF?平面EFP,∴平面EFP⊥平面BCE;
(Ⅱ)解:连接DE,由(Ⅰ)知,AE⊥平面ABCD,
∴AE⊥AD,又AB⊥AD,AE∩AD=A,
∴AB⊥平面ADE,又AB∥GE,∴GE⊥平面ADE.
∴VADC﹣BCE=
=.
∴几何体ADC﹣BCE的体积为4.
20.《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书本记载了一种名为“刍甍”的五面体(如图1).其中四边形ABCD为矩形,EF∥AB,△EAD和△FBC是三角形,“刍甍”字面意思为茅草屋顶.图2是一栋农村别墅,为全新的混凝土结构.它由上部屋顶和下部主体两部分组成.如图3,屋顶五面体为“刍甍”,其中前后两坡屋面ABEF和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形,点F在平面ABCD和BC上射影分别为H,M,已知HM=5米,BC=10米,梯形ABEF的面积是△FBC面积的2.2倍.设.
(1)求屋顶面积S关于θ的函数关系式;
(2)已知上部屋顶造价由屋顶面积确定,造价为600元/平方米,下部主体造价由高度确定,造价为9600元/米.现欲造一栋上、下总高度为6米的别墅,试问:当θ为何值时,总造价最低?
解:(1)在Rt△FHM中,FM==,
∴S△FBC=FM?BC=×10=,
∵梯形ABEF的面积是△FBC面积的2.2倍,即S梯形ABEF=2.2S△FBC,
∴屋顶面积S=2(S△FBC+S梯形ABEF)=2×3.2S△FBC=2×3.2×=,.
(2)在Rt△FHM中,FH=HM?tanθ=5tanθ,
∴下部主体的高度为6﹣5tanθ,
∴总造价y=×600+(6﹣5tanθ)×9600=9600×(+6﹣)=9600×(+6),
设f(θ)=,要使总造价最低,则f(θ)最小,
f'(θ)==,
令f'(θ)=0,则sinθ=,
∵,∴θ=,
当θ∈(0,)时,f'(θ)<0,f(θ)单调递减,当θ∈(,)时,f'(θ)>0,f(θ)单调递增,
∴当时,f(θ)取得最小值,
故当时,总造价最低.
21.已知椭圆的离心率为,点F1,F2分别为其左、右焦点,点A,B分别为其左、右顶点,点Q为椭圆上不与A,B重合的动点,且△QAF1面积的最大值为.
(1)求椭圆C的方程;
(2)分别过点A,B作直线l1⊥AQ于点A,l2⊥BQ于点B,设l1与l2相交于点P,求点P的轨迹方程.
解:(1)由题意得,即a=2c.
又,点Q为椭圆上的动点.
故|yQ|≤b,则的最大值为
即(a﹣c)2(a2﹣c2)=3,代入a=2c得c=1,故a=2,,
即椭圆方程为.
(2)设Q(x0,y0),P(x,y),则.①
由题意得:,,,,
则kAQ?kAP=﹣1,kBQ?kBP=﹣1.
且kAQ?kBQ=,代入①得,
又kAQ?kAP?kBQ?kBP=1,
所以,
即,整理得.
故为所求轨迹方程.
22.设函数.
(1)求f(x)的单调区间;
(2)求证:当x∈[1,ea]时,.
解:(1)由题意得,
令f'(x)=0,得,由f'(x)>0,得,由f'(x)<0,得,
所以f(x)的单调递增区间为,单调递减区间为;
(2)证明:若,即0<a≤2,由(1)知f(x)在[1,ea]上单调递增,
所以f(x)的最大值是f(ea)=ea﹣,若,即a>2,
设g(a)=ea﹣a,则当a>2时,g'(a)=ea﹣1>0,
所以g(a)>g(2)=e2﹣2>0,所以,从而,
结合(1)可知,f(x)在上单调递减,在上单调递增,
下面比较和f(1)=1的大小
设,当a>2时,h'(a)=ea﹣a>0,
所以h(a)>h(2)=e2﹣2>1,即f(ea)>f(1)
所以当x∈[1,ea]时,.
同课章节目录
