2020-2021学年人教版九年级数学下册 第二十九章 投影与视图之投影 习题练习(Word版 附答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册 第二十九章 投影与视图之投影 习题练习(Word版 附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 10:04:18 | ||
图片预览



文档简介
人教版九年级数学下册
第二十九章
投影与视图之投影
习题练习(附答案)
一、选择题
1.如图,方桌正上方的灯泡(看做一个点),发出的光线照射方桌后,在地面上形成阴影,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,地面上阴影部分的面积为( )
A.
3.24
m2
B.
0.36
m2
C.
1.8
m2
D.
1.44
m2
2.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为( )
A.
30°
B.
36°
C.
45°
D.
72°
3.有一圆柱形的水池,已知水池的底面直径为4米,水面离池口2米,水池内有一小青蛙,它每天晚上都会浮在水面上赏月,则它能观察到的最大视角为( )
A.
45°
B.
60°
C.
90°
D.
135°
4.当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛E距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )
A.
1米
B.
0.6米
C.
0.5米
D.
0.4米
5.如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
A.
逐渐变大
B.
逐渐变小
C.
不变
D.
无法确定
6.当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为( )
A.
汽车的速度很快
B.
盲区增大
C.
汽车的速度很慢
D.
盲区减小
7.)关于盲区的说法正确的有( )
(1)我们把视线看不到的地方称为盲区;
(2)我们上山与下山时视野盲区是相同的;
(3)我们坐车向前行驶,有时会发现一些高大的建筑物会被比较矮的建筑物挡住;
(4)人们常说“站得高,看得远”,说明在高处视野盲区要小,视野范围大.
A.
1个
B.
2个
C.
3个
D.
4个
8.人离窗子越远,向外眺望时此人的盲区是( )
A.
变小
B.
变大
C.
不变
D.
以上都有可能
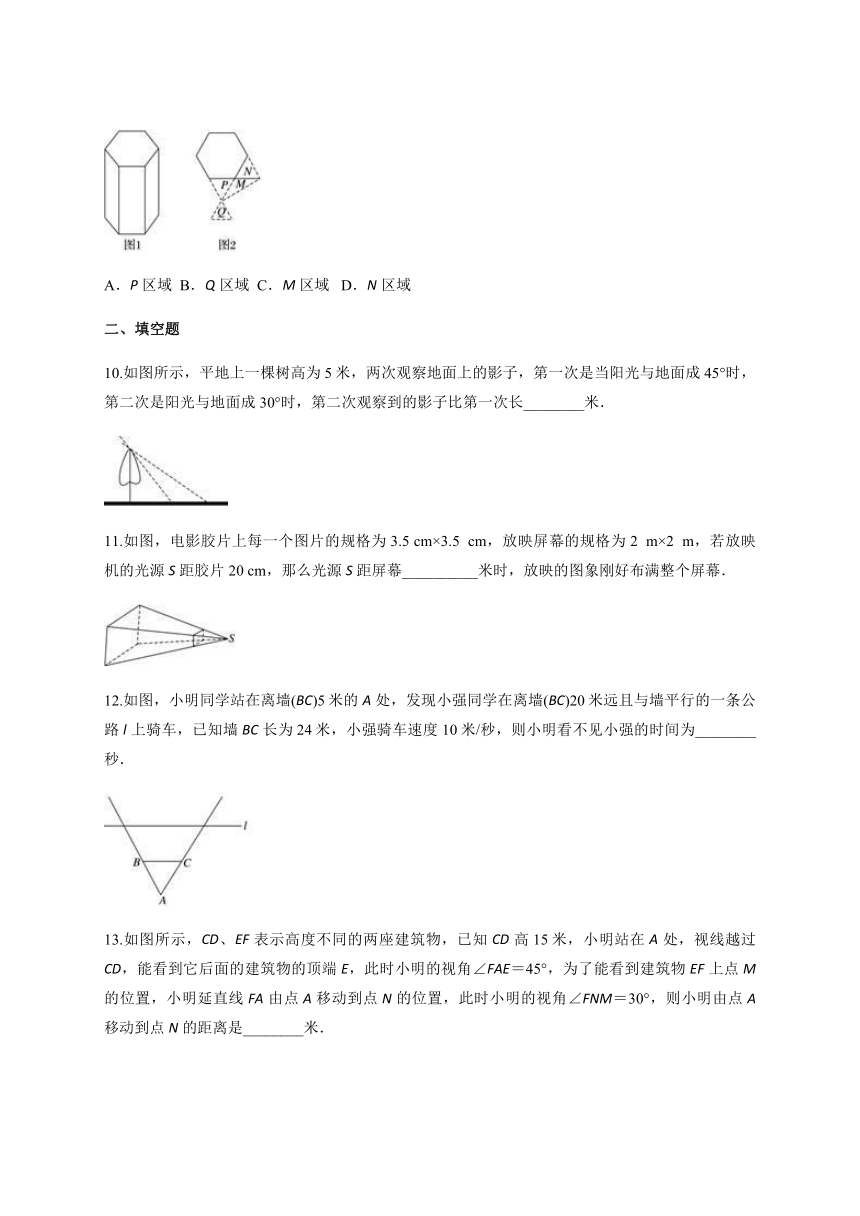
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
二、填空题
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长________米.
11.如图,电影胶片上每一个图片的规格为3.5
cm×3.5
cm,放映屏幕的规格为2
m×2
m,若放映机的光源S距胶片20
cm,那么光源S距屏幕__________米时,放映的图象刚好布满整个屏幕.
12.如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为________秒.
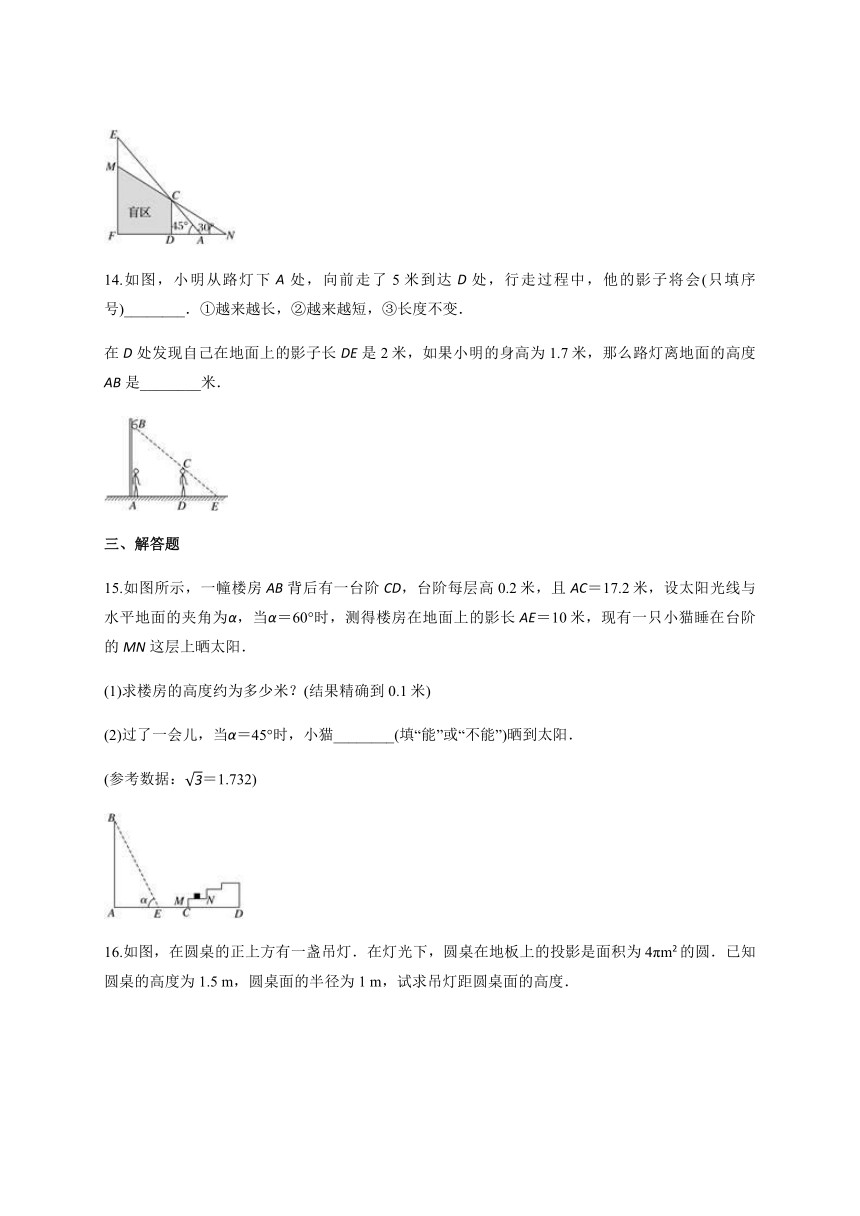
13.如图所示,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则小明由点A移动到点N的距离是________米.
14.如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)________.①越来越长,②越来越短,③长度不变.
在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是________米.
三、解答题
15.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫________(填“能”或“不能”)晒到太阳.
(参考数据:=1.732)
16.如图,在圆桌的正上方有一盏吊灯.在灯光下,圆桌在地板上的投影是面积为4πm2的圆.已知圆桌的高度为1.5
m,圆桌面的半径为1
m,试求吊灯距圆桌面的高度.
17.如示意图,小华家(点A处)和公路(l)之间竖立着一块35
m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60
km/h匀速行驶的汽车经过公路段的时间是3
s,已知广告牌和公路的距离是40
m,求小华家到公路的距离.(精确到1
m)
18.综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30
m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3
s,已知小王到广告牌和公路的距离是分别是40
m和80
m,求该汽车的速度?
19.如图,两棵树的高度分别为AB=6
m,CD=8
m,两树的根部间的距离AC=4
m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6
m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
答案解析
1.【答案】A
【解析】根据题意由图可知,====,
由于面积比等于相似比的平方,故地面上阴影部分的面积为×1.2×1.2=3.24=3.24
m2.
故选A.
2.【答案】B
【解析】由题意我们可以得出,正五棱柱的俯视图中,正五边形的内角为=108°,那么∠MPN=180°-(180°-108°)×2=36°.
故选B.
3.【答案】C
【解析】利用已知条件可以推出△OBC,△OAD均为等腰直角三角形,此时再利用已知条件就很容易求得所求的角的度数.
∵AB=4,O为圆心,
∴AO=BO=2,
∵BC=2,BC⊥AB,
∴△OBC为等腰直角三角形,
∴∠COB=45°,
同理∠AOD=45°,
∴∠COD=90°.
故选C.
4.【答案】B
【解析】由题意可知,PR=2.5
m,QR=2
m,HR=1.6
m,HE=x,
∴HQ=QR-HR=0.4
m,PH=PR-HR=0.9
m,
∵HE是圆O的切线,
∴HE2=HQ·HP,
∴x2=0.4×0.9
解得x=0.6.
故选B.
5.【答案】C
【解析】∵在小猴爬行的过程中,视线与水平方向所成角等于,竹竿与地面的夹角,
∴视线与水平方向所成角不变,
故选C.
6.【答案】B
【解析】当你乘车沿一条平坦大道向前方行驶时,人的视角变大,盲区增大,你会发现,所以前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了.
故选B.
7.【答案】C
【解析】根据视点,视角和盲区的定义进行选择.
根据视点,视角和盲区的定义,我们可以判断出(1)(3)(4)是正确的,而(2)中,要注意的是仰视时越向前视野越小盲区越大,俯视时视线越向前视野越大,盲区越小.
故选C.
8.【答案】B
【解析】如图:AB为窗子,EF∥AB,过AB的直线CD,
通过想象我们可以知道,不管在哪个区域,离窗子越远,视角就会越小,盲区就会变大.
故选B.
9.【答案】B
【解析】由图片可知,只有Q区域同时处在三个侧面的观察范围内.
故选B.
10.【答案】(5-5)
【解析】如图所示:
∵第一次是当阳光与地面成45°,
∴AB=BC=5
m,
∵第二次是阳光与地面成30°,
∴BD==5(m),
∴第二次观察到的影子比第一次长(5-5)
m.
故答案为(5-5)
11.【答案】
【解析】∵△SPE∽△SBC,
∴=,
又∵PE=3.5
cm,BC=200
cm,SR=20
cm,
∴=,
解得SD=cm=m.
故答案为.
12.【答案】12
【解析】如图,
∵BC∥DE,
∴△ABC∽△ADE,
∴BC∶DE=5∶25,
∵BC=24米,
∴DE=120米,
∵小强骑车速度10米/秒,
∴120÷10=12(秒),
故答案为12.
13.【答案】15-15
【解析】直角三角形CDN中,DN=CD÷tan
30°=15米,
直角三角形CDA中,AD=CD÷tan
45°=15米,
因此,AN=DN-AD=(15-15)米.
14.【答案】① 5.95
【解析】小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会越来越长;
∵CD∥AB,
∴△ECD∽△EBA,
∴=,=,
∴AB=5.95(m).
故答案为①,5.95.
15.【答案】解 (1)当α=60°时,在Rt△ABE中,
∵tan
60°==,
∴AB=10·tan
60°=10≈10×1.73=17.3(米).
即楼房的高度约为17.3米;
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan
45°==1,
此时的影长AF=AB=17.3米,
∴CF=AF-AC=17.3-17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫能晒到太阳.
【解析】(1)在Rt△ABE中,由tan
60°==,即可求出AB的长;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF-AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
16.【答案】解 ∵圆桌面的半径为1
m,
∴圆桌面的面积为πm2,
∴=,
∵AB∥CD,
∴△PAB∽△PCD,
∴=,
∵圆桌的高度为1.5
m,
∴=,
∴解得PA=1.5(m),
答:吊灯距圆桌面的高度为1.5
m.
【解析】首先求出圆桌的面积,进而利用相似三角形的性质得出面积比为1∶4,则相似比为1∶2,即可得出PA的长.
17.【答案】解 如图,连接AD、AE,并延长分别交l于B、C,则CBDE为视点A的盲区,BC=60
000×=50(m).
过A点作AM⊥BC于M,交DE于N,则AN⊥DE,MN=40
m.
由△ADE∽△ABC,得==,
即=,所以AM≈133(米).
即小华家到公路的距离约为133米.
【解析】根据盲区的定义,作出盲区,然后即可以通过相似三角形的性质求出距离.
18.【答案】解 (1)如图,作射线AD、AE,分别交L于点B、C,BC即为视点A的盲区在公路上的那段.
(2)过点A作AF⊥BC,垂足为点F,交DE于点H.
∵DE∥BC.
∴∠ADE=∠ABC,∠DAE=∠BAC.
∴△ADE∽△ABC,
∴=,
由题意知,DE=30,AF=80,HA=40,
∴=,
∴=,
∴BC=60
m,
∵一辆匀速行驶的汽车经过公路BC段的时间是3
s,
∴该汽车的速度为60÷3=20(m/s),
答:该汽车的速度是20米/秒.
【解析】(1)作射线AD、AE分别于L相交于点B、C,然后即可确定盲区;
(2)先根据路程=速度×时间求出BC的长度,然后过点A作AF⊥BC,根据相似三角形对应高的比等于对应边的比列出比例式,求出BC的长,即可得出汽车速度.
19.【答案】解 设FG=x米.那么FH=x+GH=x+AC=x+4(米),
∵AB=6
m,CD=8
m,小强的眼睛与地面的距离为1.6
m,
∴BG=4.4
m,DH=6.4
m,
∵BA⊥PC,CD⊥PC,
∴AB∥CD,
∴FG∶FH=BG∶DH,即FG·DH=FH·BG,
∴x×6.4=(x+4)×4.4,
解得x=8.8(米),
因此小于8.8米时就看不到树CD的树顶D.
【解析】根据盲区的定义结合图片,我们可看出在FG之间时,是看不到树CD的树顶D的.因此求出FG就是本题的关键.
已知了AC的长,BG、DH的长,那么可根据平行线分线段成比例来得出关于FG、FH、BG、DH的比例关系式,用FG表示出FG后即可求出FG的长.
第二十九章
投影与视图之投影
习题练习(附答案)
一、选择题
1.如图,方桌正上方的灯泡(看做一个点),发出的光线照射方桌后,在地面上形成阴影,已知方桌边长1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,地面上阴影部分的面积为( )
A.
3.24
m2
B.
0.36
m2
C.
1.8
m2
D.
1.44
m2
2.图(1)表示一个正五棱柱形状的高大建筑物,图(2)是它的俯视图.小健站在地面观察该建筑物,当他在图(2)中的阴影部分所表示的区域活动时,能同时看到建筑物的三个侧面,图中∠MPN的度数为( )
A.
30°
B.
36°
C.
45°
D.
72°
3.有一圆柱形的水池,已知水池的底面直径为4米,水面离池口2米,水池内有一小青蛙,它每天晚上都会浮在水面上赏月,则它能观察到的最大视角为( )
A.
45°
B.
60°
C.
90°
D.
135°
4.当你站在博物馆的展览厅中时,你知道站在何处观赏最理想吗?如图,设墙壁上的展品最高点P距地面2.5米,最低点Q距地面2米,观赏者的眼睛E距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E到墙壁的距离为( )
A.
1米
B.
0.6米
C.
0.5米
D.
0.4米
5.如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
A.
逐渐变大
B.
逐渐变小
C.
不变
D.
无法确定
6.当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为( )
A.
汽车的速度很快
B.
盲区增大
C.
汽车的速度很慢
D.
盲区减小
7.)关于盲区的说法正确的有( )
(1)我们把视线看不到的地方称为盲区;
(2)我们上山与下山时视野盲区是相同的;
(3)我们坐车向前行驶,有时会发现一些高大的建筑物会被比较矮的建筑物挡住;
(4)人们常说“站得高,看得远”,说明在高处视野盲区要小,视野范围大.
A.
1个
B.
2个
C.
3个
D.
4个
8.人离窗子越远,向外眺望时此人的盲区是( )
A.
变小
B.
变大
C.
不变
D.
以上都有可能
9.图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P、Q、M、N表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )
A.P区域
B.Q区域
C.M区域
D.N区域
二、填空题
10.如图所示,平地上一棵树高为5米,两次观察地面上的影子,第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长________米.
11.如图,电影胶片上每一个图片的规格为3.5
cm×3.5
cm,放映屏幕的规格为2
m×2
m,若放映机的光源S距胶片20
cm,那么光源S距屏幕__________米时,放映的图象刚好布满整个屏幕.
12.如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为________秒.
13.如图所示,CD、EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,则小明由点A移动到点N的距离是________米.
14.如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号)________.①越来越长,②越来越短,③长度不变.
在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是________米.
三、解答题
15.如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫________(填“能”或“不能”)晒到太阳.
(参考数据:=1.732)
16.如图,在圆桌的正上方有一盏吊灯.在灯光下,圆桌在地板上的投影是面积为4πm2的圆.已知圆桌的高度为1.5
m,圆桌面的半径为1
m,试求吊灯距圆桌面的高度.
17.如示意图,小华家(点A处)和公路(l)之间竖立着一块35
m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60
km/h匀速行驶的汽车经过公路段的时间是3
s,已知广告牌和公路的距离是40
m,求小华家到公路的距离.(精确到1
m)
18.综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30
m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3
s,已知小王到广告牌和公路的距离是分别是40
m和80
m,求该汽车的速度?
19.如图,两棵树的高度分别为AB=6
m,CD=8
m,两树的根部间的距离AC=4
m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为1.6
m,当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
答案解析
1.【答案】A
【解析】根据题意由图可知,====,
由于面积比等于相似比的平方,故地面上阴影部分的面积为×1.2×1.2=3.24=3.24
m2.
故选A.
2.【答案】B
【解析】由题意我们可以得出,正五棱柱的俯视图中,正五边形的内角为=108°,那么∠MPN=180°-(180°-108°)×2=36°.
故选B.
3.【答案】C
【解析】利用已知条件可以推出△OBC,△OAD均为等腰直角三角形,此时再利用已知条件就很容易求得所求的角的度数.
∵AB=4,O为圆心,
∴AO=BO=2,
∵BC=2,BC⊥AB,
∴△OBC为等腰直角三角形,
∴∠COB=45°,
同理∠AOD=45°,
∴∠COD=90°.
故选C.
4.【答案】B
【解析】由题意可知,PR=2.5
m,QR=2
m,HR=1.6
m,HE=x,
∴HQ=QR-HR=0.4
m,PH=PR-HR=0.9
m,
∵HE是圆O的切线,
∴HE2=HQ·HP,
∴x2=0.4×0.9
解得x=0.6.
故选B.
5.【答案】C
【解析】∵在小猴爬行的过程中,视线与水平方向所成角等于,竹竿与地面的夹角,
∴视线与水平方向所成角不变,
故选C.
6.【答案】B
【解析】当你乘车沿一条平坦大道向前方行驶时,人的视角变大,盲区增大,你会发现,所以前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了.
故选B.
7.【答案】C
【解析】根据视点,视角和盲区的定义进行选择.
根据视点,视角和盲区的定义,我们可以判断出(1)(3)(4)是正确的,而(2)中,要注意的是仰视时越向前视野越小盲区越大,俯视时视线越向前视野越大,盲区越小.
故选C.
8.【答案】B
【解析】如图:AB为窗子,EF∥AB,过AB的直线CD,
通过想象我们可以知道,不管在哪个区域,离窗子越远,视角就会越小,盲区就会变大.
故选B.
9.【答案】B
【解析】由图片可知,只有Q区域同时处在三个侧面的观察范围内.
故选B.
10.【答案】(5-5)
【解析】如图所示:
∵第一次是当阳光与地面成45°,
∴AB=BC=5
m,
∵第二次是阳光与地面成30°,
∴BD==5(m),
∴第二次观察到的影子比第一次长(5-5)
m.
故答案为(5-5)
11.【答案】
【解析】∵△SPE∽△SBC,
∴=,
又∵PE=3.5
cm,BC=200
cm,SR=20
cm,
∴=,
解得SD=cm=m.
故答案为.
12.【答案】12
【解析】如图,
∵BC∥DE,
∴△ABC∽△ADE,
∴BC∶DE=5∶25,
∵BC=24米,
∴DE=120米,
∵小强骑车速度10米/秒,
∴120÷10=12(秒),
故答案为12.
13.【答案】15-15
【解析】直角三角形CDN中,DN=CD÷tan
30°=15米,
直角三角形CDA中,AD=CD÷tan
45°=15米,
因此,AN=DN-AD=(15-15)米.
14.【答案】① 5.95
【解析】小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会越来越长;
∵CD∥AB,
∴△ECD∽△EBA,
∴=,=,
∴AB=5.95(m).
故答案为①,5.95.
15.【答案】解 (1)当α=60°时,在Rt△ABE中,
∵tan
60°==,
∴AB=10·tan
60°=10≈10×1.73=17.3(米).
即楼房的高度约为17.3米;
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan
45°==1,
此时的影长AF=AB=17.3米,
∴CF=AF-AC=17.3-17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫能晒到太阳.
【解析】(1)在Rt△ABE中,由tan
60°==,即可求出AB的长;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF-AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
16.【答案】解 ∵圆桌面的半径为1
m,
∴圆桌面的面积为πm2,
∴=,
∵AB∥CD,
∴△PAB∽△PCD,
∴=,
∵圆桌的高度为1.5
m,
∴=,
∴解得PA=1.5(m),
答:吊灯距圆桌面的高度为1.5
m.
【解析】首先求出圆桌的面积,进而利用相似三角形的性质得出面积比为1∶4,则相似比为1∶2,即可得出PA的长.
17.【答案】解 如图,连接AD、AE,并延长分别交l于B、C,则CBDE为视点A的盲区,BC=60
000×=50(m).
过A点作AM⊥BC于M,交DE于N,则AN⊥DE,MN=40
m.
由△ADE∽△ABC,得==,
即=,所以AM≈133(米).
即小华家到公路的距离约为133米.
【解析】根据盲区的定义,作出盲区,然后即可以通过相似三角形的性质求出距离.
18.【答案】解 (1)如图,作射线AD、AE,分别交L于点B、C,BC即为视点A的盲区在公路上的那段.
(2)过点A作AF⊥BC,垂足为点F,交DE于点H.
∵DE∥BC.
∴∠ADE=∠ABC,∠DAE=∠BAC.
∴△ADE∽△ABC,
∴=,
由题意知,DE=30,AF=80,HA=40,
∴=,
∴=,
∴BC=60
m,
∵一辆匀速行驶的汽车经过公路BC段的时间是3
s,
∴该汽车的速度为60÷3=20(m/s),
答:该汽车的速度是20米/秒.
【解析】(1)作射线AD、AE分别于L相交于点B、C,然后即可确定盲区;
(2)先根据路程=速度×时间求出BC的长度,然后过点A作AF⊥BC,根据相似三角形对应高的比等于对应边的比列出比例式,求出BC的长,即可得出汽车速度.
19.【答案】解 设FG=x米.那么FH=x+GH=x+AC=x+4(米),
∵AB=6
m,CD=8
m,小强的眼睛与地面的距离为1.6
m,
∴BG=4.4
m,DH=6.4
m,
∵BA⊥PC,CD⊥PC,
∴AB∥CD,
∴FG∶FH=BG∶DH,即FG·DH=FH·BG,
∴x×6.4=(x+4)×4.4,
解得x=8.8(米),
因此小于8.8米时就看不到树CD的树顶D.
【解析】根据盲区的定义结合图片,我们可看出在FG之间时,是看不到树CD的树顶D的.因此求出FG就是本题的关键.
已知了AC的长,BG、DH的长,那么可根据平行线分线段成比例来得出关于FG、FH、BG、DH的比例关系式,用FG表示出FG后即可求出FG的长.
