三视图2
图片预览



文档简介
(共17张PPT)
人教版教材九年级数学下册
29.2 三视图 (2)
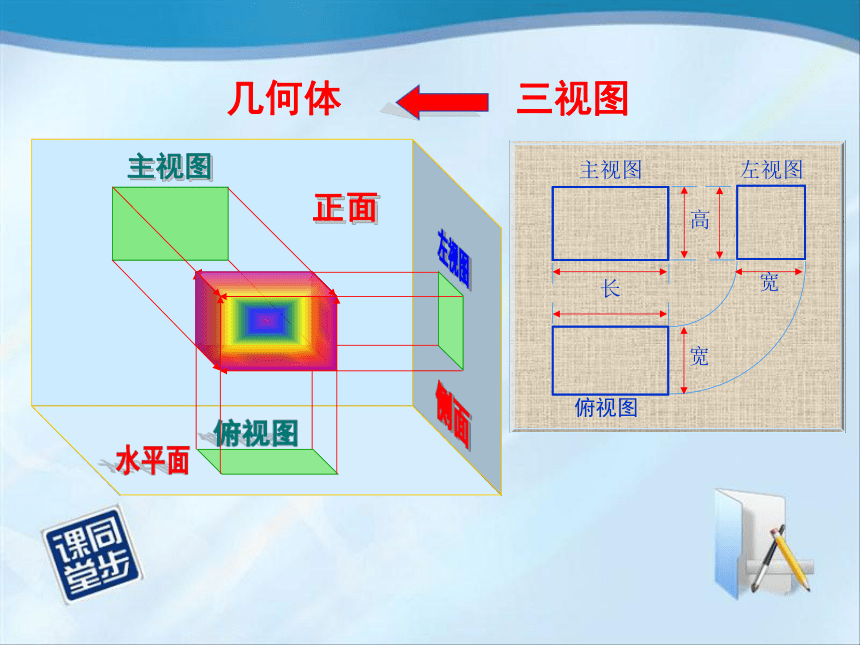
主视图
主视图
左视图
正面
几何体 三视图
高
长
宽
宽
俯视图
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据三视图想象从不同方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
一:归纳步骤:
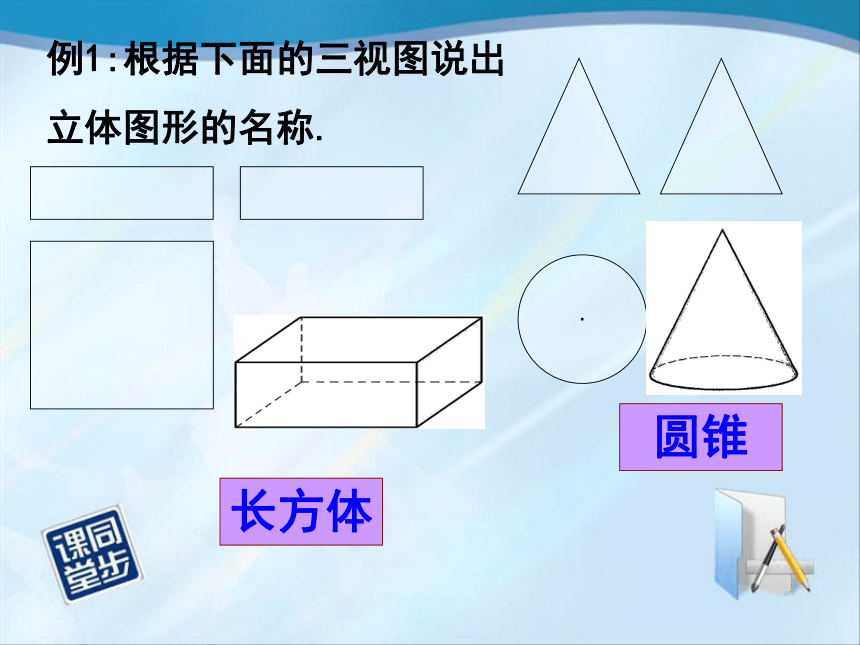
长方体
·
圆锥
例1:根据下面的三视图说出
立体图形的名称.
下列是一个物体的三视图,请描述出它的形状
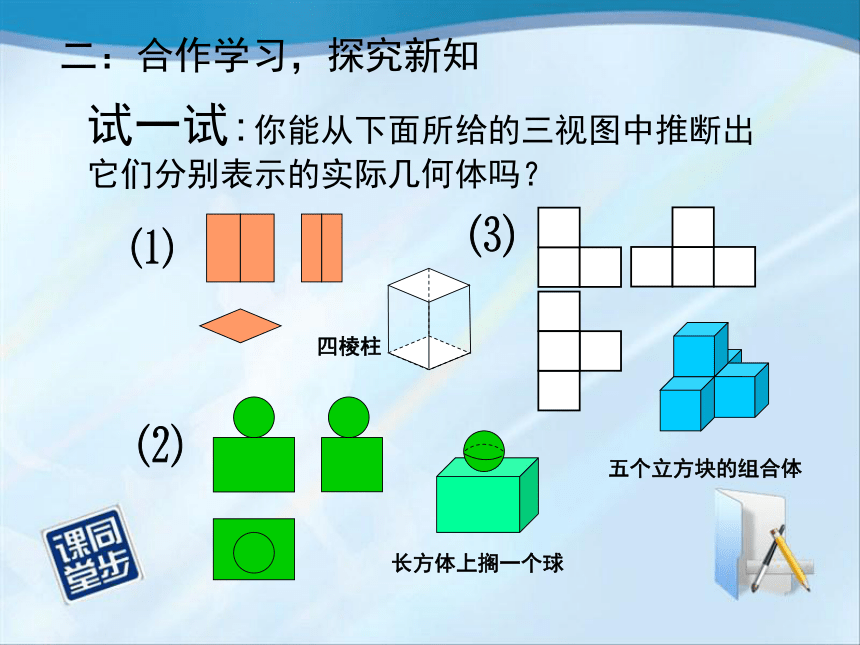
试一试:你能从下面所给的三视图中推断出它们分别表示的实际几何体吗?
四棱柱
长方体上搁一个球
二:合作学习,探究新知
五个立方块的组合体
9
6
4.5
3
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢
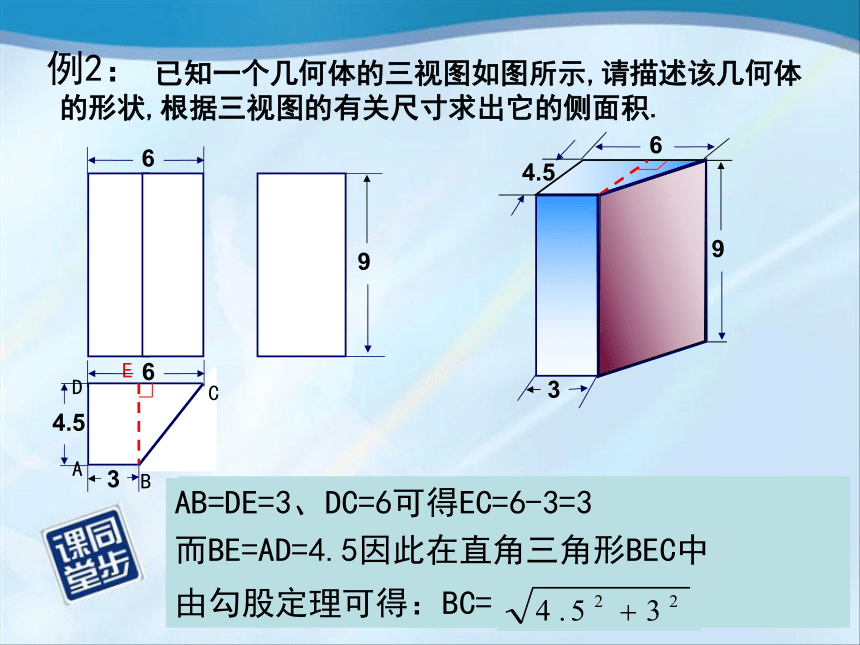
已知一个几何体的三视图如图所示,请描述该几何体的形状,根据三视图的有关尺寸求出它的侧面积.
由主视图、左视图推测,这个几何体可能是直棱柱, 但不能确定棱的条数. 再由俯视图可以确定它是直四棱柱,且底面是梯形.
例2:
A
B
C
D
E
AB=DE=3、DC=6可得EC=6-3=3
而BE=AD=4.5因此在直角三角形BEC中
由勾股定理可得:BC=
6
9
3
4.5
6
9
6
4.5
3
解 : 作上底面的高.根据三视图可知这个几何体是底面为梯形的直四棱柱.根据三视图的有关尺寸,可得这个直四棱柱的对应尺寸:它的四个侧面都是长为9的长方形,前后两个侧面的宽分别为3、6,左侧面的宽为4.5,由勾股定理可得,
右侧面的宽是: .
答:这个几何体的侧面积为170.2
所以它的侧面积为
2
2
)
3
6
(
5
.
4
9
5
.
4
9
6
9
3
-
+
+
+
+
×
×
×
×
9
≈170.2
练一练:
(1)某物体的三视图如图所示。请说出它的形状。
三棱柱
下列是一个物体的三视图,请描述出它的形状
三棱锥
这是一个立体图形的三视图,你能说出它的名称 吗?
圆柱
四棱锥
下列是一个物体的三视图,请描述出它的形状
如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
你能摆出这个几何体吗?
试画出这个几何体的主视图与左视图。
主视图
左视图
1
1
2
2
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭法(你可以用实物模型动手试一试) 你能用三视图表示你探究的结果吗
思考题:
作业布置:
必做题:P/116—117 第4、5、8题
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广应用.那么怎样由三视图得到几何体呢?今天我们一块儿来研究一下这个课题.
人教版教材九年级数学下册
29.2 三视图 (2)
主视图
主视图
左视图
正面
几何体 三视图
高
长
宽
宽
俯视图
由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据三视图想象从不同方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
一:归纳步骤:
长方体
·
圆锥
例1:根据下面的三视图说出
立体图形的名称.
下列是一个物体的三视图,请描述出它的形状
试一试:你能从下面所给的三视图中推断出它们分别表示的实际几何体吗?
四棱柱
长方体上搁一个球
二:合作学习,探究新知
五个立方块的组合体
9
6
4.5
3
从图上看出有五个面的面积可以直接求出,关键只要求出另个侧面的面积就行了,怎样求呢
已知一个几何体的三视图如图所示,请描述该几何体的形状,根据三视图的有关尺寸求出它的侧面积.
由主视图、左视图推测,这个几何体可能是直棱柱, 但不能确定棱的条数. 再由俯视图可以确定它是直四棱柱,且底面是梯形.
例2:
A
B
C
D
E
AB=DE=3、DC=6可得EC=6-3=3
而BE=AD=4.5因此在直角三角形BEC中
由勾股定理可得:BC=
6
9
3
4.5
6
9
6
4.5
3
解 : 作上底面的高.根据三视图可知这个几何体是底面为梯形的直四棱柱.根据三视图的有关尺寸,可得这个直四棱柱的对应尺寸:它的四个侧面都是长为9的长方形,前后两个侧面的宽分别为3、6,左侧面的宽为4.5,由勾股定理可得,
右侧面的宽是: .
答:这个几何体的侧面积为170.2
所以它的侧面积为
2
2
)
3
6
(
5
.
4
9
5
.
4
9
6
9
3
-
+
+
+
+
×
×
×
×
9
≈170.2
练一练:
(1)某物体的三视图如图所示。请说出它的形状。
三棱柱
下列是一个物体的三视图,请描述出它的形状
三棱锥
这是一个立体图形的三视图,你能说出它的名称 吗?
圆柱
四棱锥
下列是一个物体的三视图,请描述出它的形状
如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
你能摆出这个几何体吗?
试画出这个几何体的主视图与左视图。
主视图
左视图
1
1
2
2
用6个相同的小方块搭成一个几何体,它的俯视图如图3-25所示.则一共有几种不同形状的搭法(你可以用实物模型动手试一试) 你能用三视图表示你探究的结果吗
思考题:
作业布置:
必做题:P/116—117 第4、5、8题
由于三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等,因此三视图在许多行业有着广应用.那么怎样由三视图得到几何体呢?今天我们一块儿来研究一下这个课题.
