切线性质与判定应用

(共16张PPT)
切线性质与判定应用
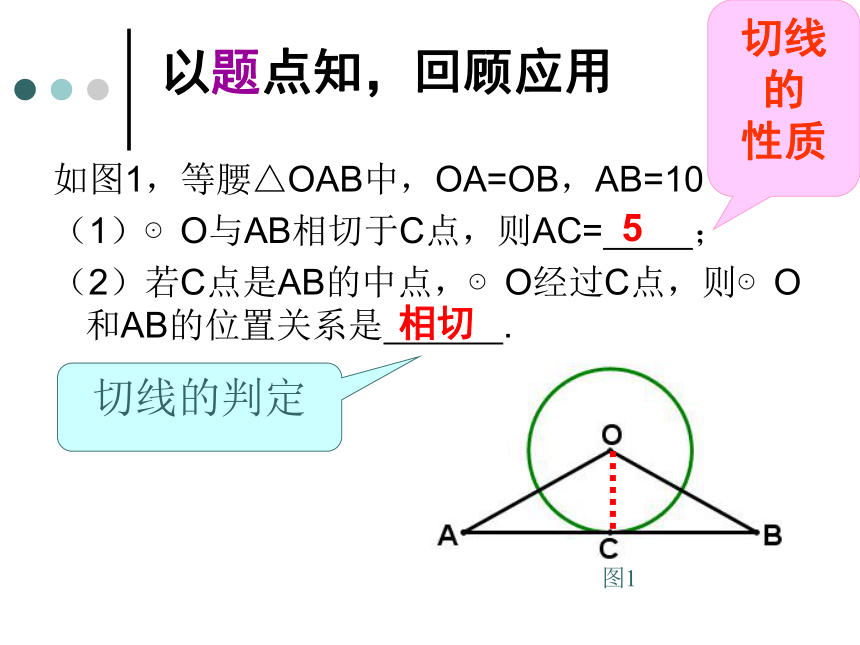
如图1，等腰△OAB中，OA=OB，AB=10
（1）⊙O与AB相切于C点，则AC= ；
（2）若C点是AB的中点，⊙O经过C点，则⊙O和AB的位置关系是 .
图1
以题点知，回顾应用
5
相切
切线的
性质
切线的判定
典例分析，学习共享
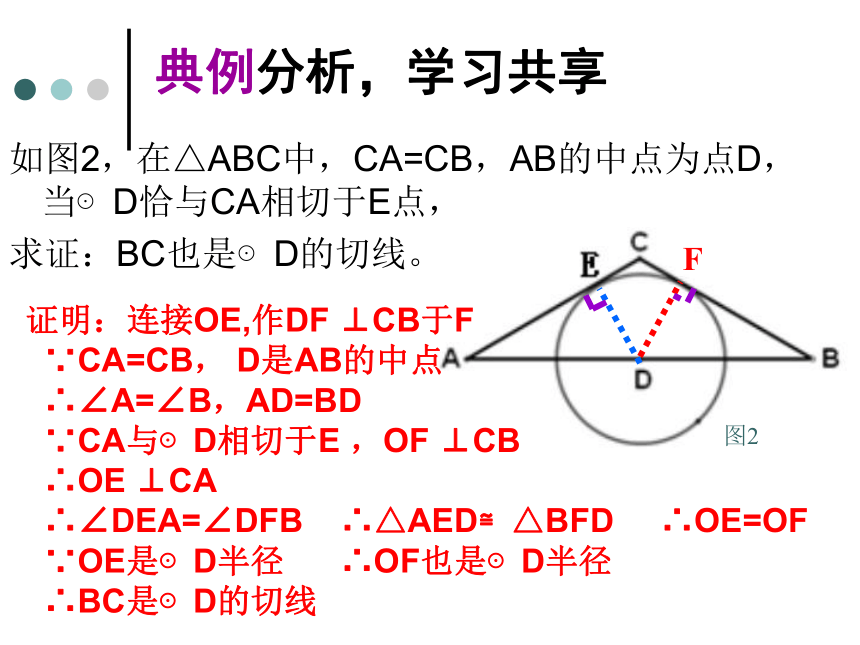
如图2，在△ABC中，CA=CB，AB的中点为点D，当⊙D恰与CA相切于E点，
求证：BC也是⊙D的切线。
图2
证明：连接OE,作DF ⊥CB于F
∵CA=CB， D是AB的中点
∴∠A=∠B，AD=BD
∵CA与⊙D相切于E ，OF ⊥CB
∴OE ⊥CA
∴∠DEA=∠DFB ∴△AED≌△BFD ∴OE=OF
∵OE是⊙D半径 ∴OF也是⊙D半径
∴BC是⊙D的切线
F
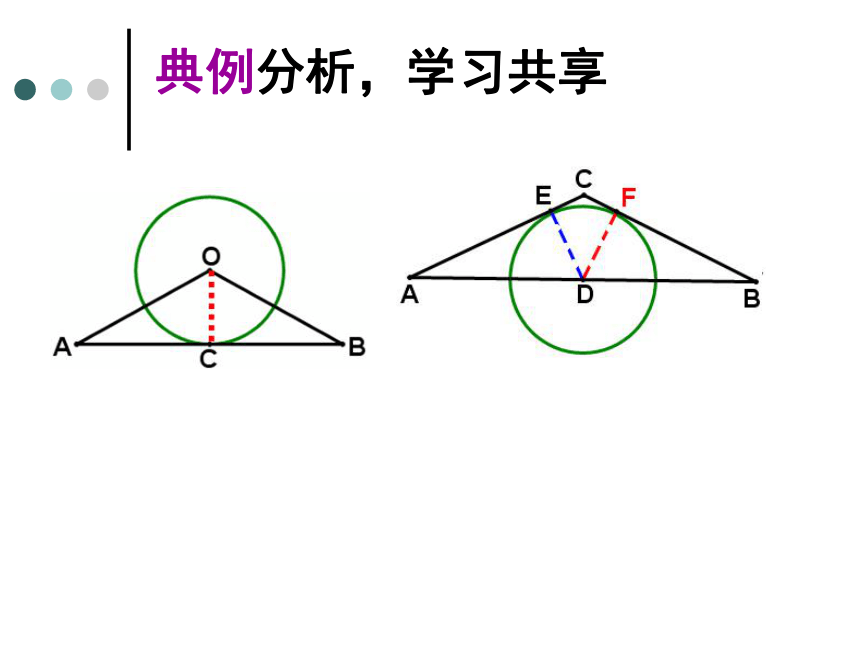
典例分析，学习共享
技能训练，提高有效
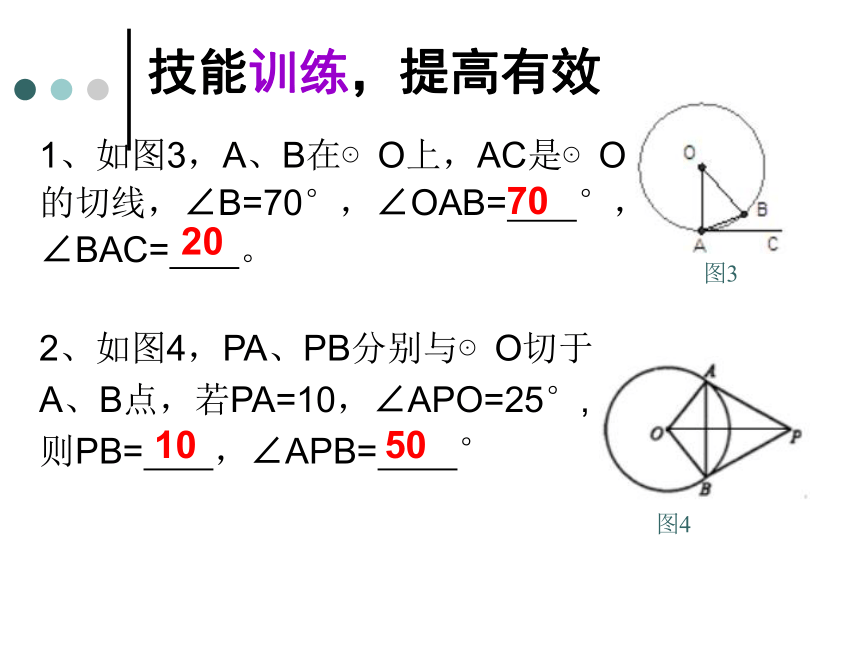
1、如图3，A、B在⊙O上，AC是⊙O
的切线，∠B=70°，∠OAB= °，
∠BAC= 。
2、如图4，PA、PB分别与⊙O切于
A、B点，若PA=10，∠APO=25°,
则PB= ，∠APB= °
70
10
图3
20
50
图4
技能训练，提高有效
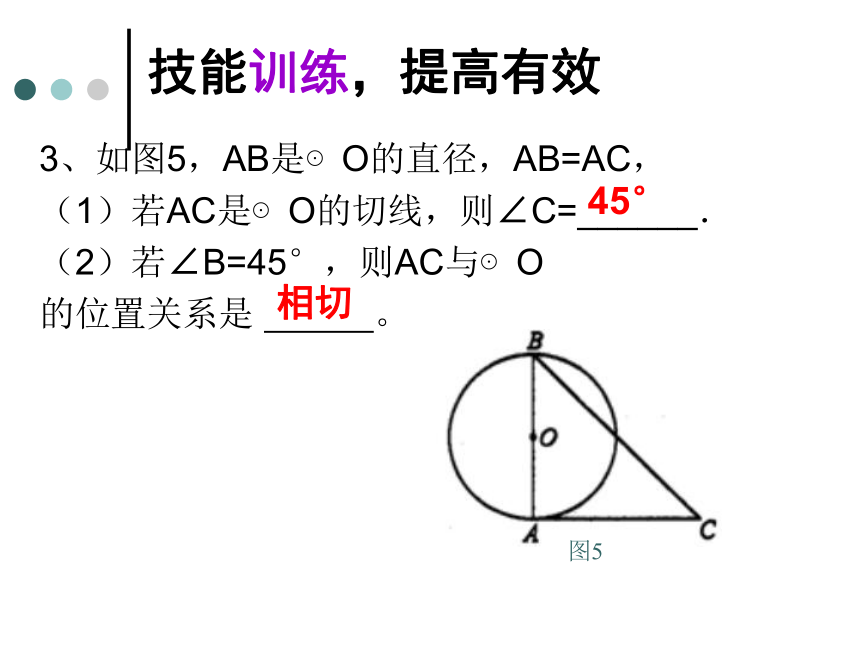
3、如图5，AB是⊙O的直径，AB=AC，
（1）若AC是⊙O的切线，则∠C=______．
（2）若∠B=45°，则AC与⊙O
的位置关系是 。
相切
45°
图5
技能训练，提高有效
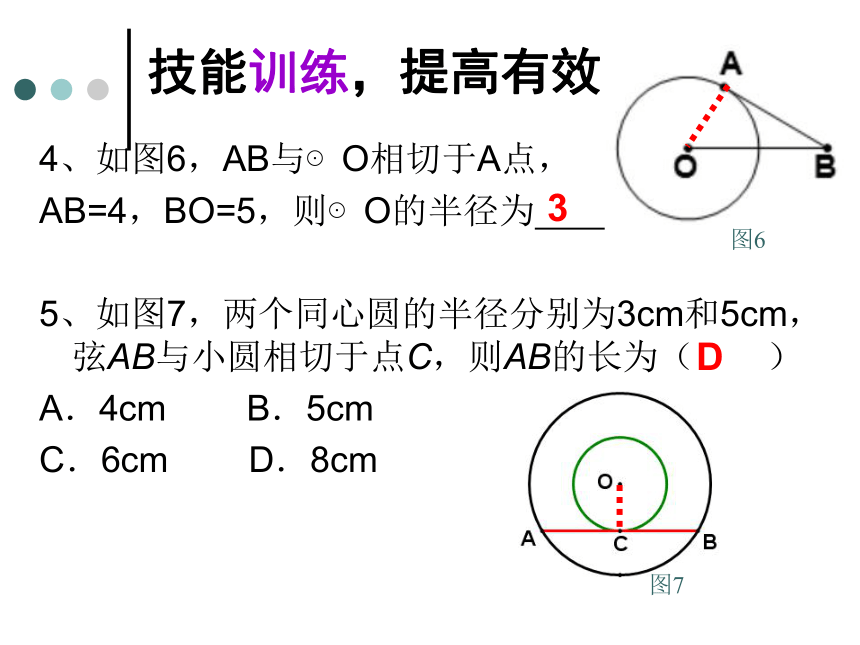
4、如图6，AB与⊙O相切于A点，
AB=4，BO=5，则⊙O的半径为 。
5、如图7，两个同心圆的半径分别为3cm和5cm，弦AB与小圆相切于点C，则AB的长为（　　）
A．4cm B．5cm
C．6cm D．8cm
D
3
图6
图7
6、如图8，已知O为∠BAC平分线上一点，
OD⊥AB于D, 以O为圆心，OD为半径作⊙O.
求证：⊙O与AC相切.
证明：过O作OE⊥AC于E
∵OA平分∠BAC，OD⊥AB
∴OD=OE
∵OD为⊙O半径
∴OE是⊙O半径
∴⊙O与AC相切
图8
技能训练，提高有效
E
火眼金睛，找出共性
轴对称性
火眼金睛，找出共性
目标检测，落实重点
1、如图9，⊙O是△ABC的内切圆，
若∠OBC=15°，∠OCB=40°，
则∠A= °
2、如图10，AB是⊙O的直径，AC是⊙O的切线，
A为切点，连结BC交⊙O于点D，
连结AD，若∠ABC=45 ° ，
则下列结论正确的是（ ）
A．BC=2AD B．AC=2AD
C．AC＞AB D．AD＞DC
A
70
图9
图10
3、如图11，在⊙O中，AB为⊙O的直径，
AC是弦， ，
（1）求∠AOC的度数；
（2）P为直径BA延长线上的一点，
当CP与⊙O相切时，求PO的长；
图18
目标检测，落实重点
解：（1）∵OC=OA，
∠OAC=60°
∴∠CAO=∠OAC=60°
∴∠AOC=60°
图11
3、如图11，在⊙O中，AB为⊙O的直径，
AC是弦， ，
（1）求∠AOC的度数；
（2）P为直径BA延长线上的一点，
当CP与⊙O相切时，求PO的长；
目标检测，落实重点
解：（2）∵CP与⊙O相切
∴OC⊥PC
∴∠PCO=90°
∵∠AOC=60°
∴OP=2CO=2×4=8
图11
目标检测，落实重点
4、如图12， AB是⊙O的弦，点C是 的中点,
直线CD∥AB. 求证：CD是⊙O的切线.
证明：连接OC.
∵C是 的中点
∴OC⊥AB
∵CD∥AB
∴OC⊥CD
∴CD是⊙O的切线
图12
如图13，如图，在△ABC中，AB=AC，内切圆O与边BC、AC、AB分别切于D、E、F.
（1）求证：BF=CE；
（2）连结AD，△ADC是什么三角形？
（3）若∠C=30°， ，求AC.
图13
拓展探索，展翅高飞