切线性质与判定应用教学设计
文档属性
| 名称 | 切线性质与判定应用教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 136.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-04 00:00:00 | ||
图片预览

文档简介
切线性质与判定的应用
【教学目标】
(1)知识与技能
①通过再现切线的判定和性质的形成过程及以题点知的练习回顾知识,并形成相应的知识结构;
②举例说明切线的性质与判定的应用,简要说出“切线”与“垂直”的密切关系(“半径”纽带的辅助作用);
③通过题组训练,有效提升应用切线的判定和性质解决问题的技能。
(2)过程与方法
①借助典型例题交流学习,发现通性,归纳分享解题思路和一般规律;
②类比例题与技能训练题的解题通性方法,分析对几何图形的分解与知识之间的转化技巧。
(3)情感、态度与价值观
说出切线在解决直线与圆的相关问题的作用,克服复习疲态,体会“课课有新知”,逐渐树立获取解题思路和方法的类比与归纳意识。
【教学重点】切线的性质和判定的应用。
【教学难点】判定切线的证明方法。
【设计说明】本课时是九年级总复习《圆》中的第4节,前面学生已复习了圆的基本概念、圆中的计算以及与圆的位置关系。本设计面向中下层次学生。针对切线的判定与性质在证明题、计算题中有较多的应用,所以本设计定位是切线判定的证明方法归纳总结,利用切线性质进行线段和角等简单计算的训练。
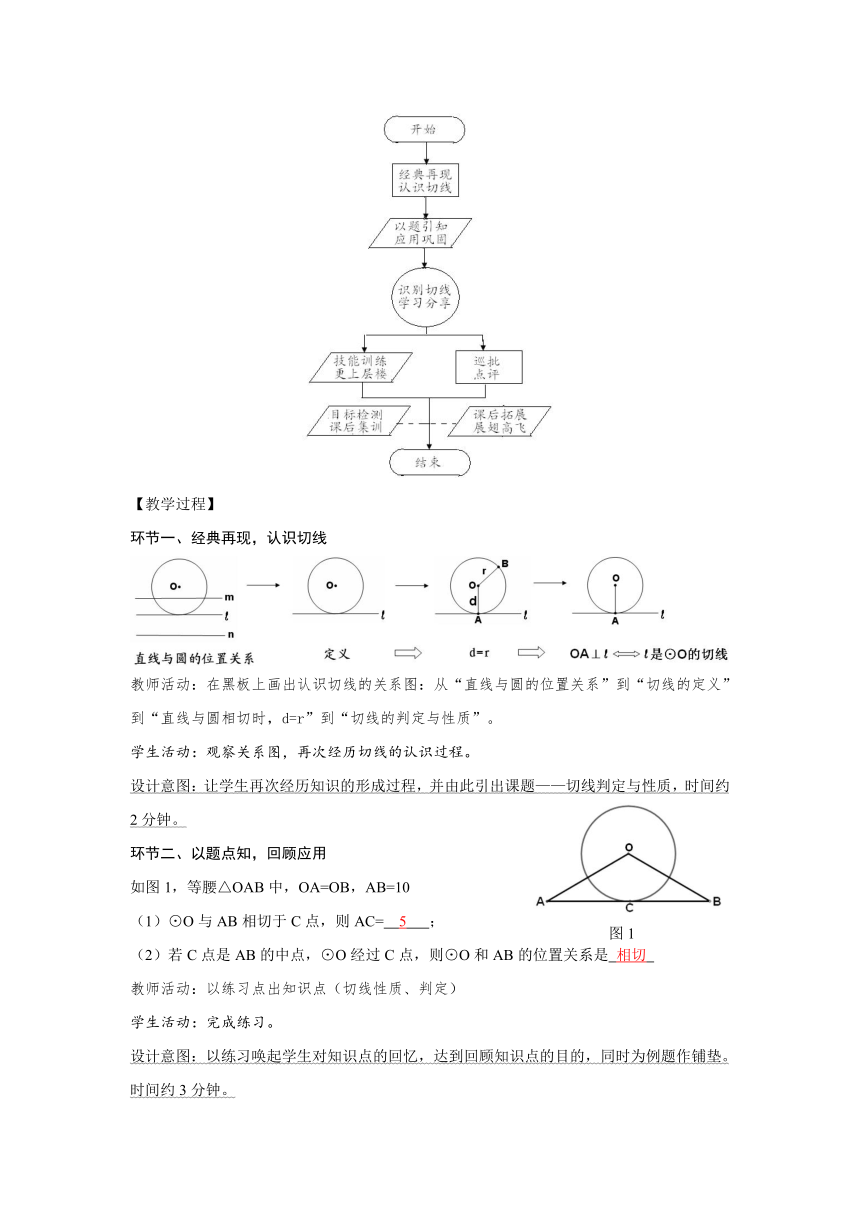
【教学流程】
【教学过程】
环节一、经典再现,认识切线
教师活动:在黑板上画出认识切线的关系图:从“直线与圆的位置关系”到“切线的定义”到“直线与圆相切时,d=r”到“切线的判定与性质”。
学生活动:观察关系图,再次经历切线的认识过程。
设计意图:让学生再次经历知识的形成过程,并由此引出课题——切线判定与性质,时间约2分钟。
环节二、以题点知,回顾应用
如图1,等腰△OAB中,OA=OB,AB=10
(1)⊙O与AB相切于C点,则AC= 5 ;
(2)若C点是AB的中点,⊙O经过C点,则⊙O和AB的位置关系是 相切
教师活动:以练习点出知识点(切线性质、判定)
学生活动:完成练习。
设计意图:以练习唤起学生对知识点的回忆,达到回顾知识点的目的,同时为例题作铺垫。时间约3分钟。
环节三、典例分析,学习共享
例、如图2,在△ABC中,CA=CB,AB的中点为点D,
当⊙D恰与CA相切于E点,求证:BC也是⊙D的切线。
证明:(2)连接DE,过D点作DF⊥CB于F点
∵⊙D恰与CA相切于E点, ∴DE⊥CA ∵DF⊥CB
∴∠AED=∠BFD=90° ∵CA=CB,∴∠A=∠B
∵AB的中点为点D ∴AD=BD ∴△ADE≌△BDF ∴DE=DF
∵DE是⊙D半径 ∴DF是⊙D半径 ∴BC也是⊙D的切线
(另外,可以也连接CD,用角平分线性质定理证明DE=DF)
教师活动:引导学生归纳常见判定切线的基本证明方法,
学生活动:先限时5分钟独立完成例题,然后小组合作归纳判定切线的证明方法。
设计意图:巩固切线的基本判定方法是本课的重点,这里先给足够时间学生独立完成例题,然后师生共享解题思路,达到学生自主学习的目的。时间约15分钟。
环节四、技能训练,提高有效
1、如图3,A、B在⊙O上,AC是⊙O的切线,
∠B=70°,则∠OAB= 70 °,∠BAC= 20 °
2、如图4,PA、PB分别与⊙O切于A、B点,
若PA=10,∠APO=25°,则PB= 10 ,∠APB= 50 °
3、如图5,AB是⊙O的直径,AB=AC,
(1)若AC是⊙O的切线,则∠C=_45_°.
(2)若∠B=45°,则AC与⊙O的位置关系是 相切
4、如图6,AB与⊙O相切于A点,AB=4,BO=5
则⊙O的半径为 3 。
5、如图7,两个同心圆的半径分别为3cm和5cm,弦AB与
小圆相切于点C,则AB的长为(D)
A.4cm B.5cm C.6cm D.8cm
6、如图8,已知O为∠BAC平分线上一点,
OD⊥AB于D, 以O为圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
证明:过O点作OE⊥AC于E
∵OA平分∠BAC,OD⊥AB
∴OD=OE
∵OD为⊙O半径
∴OE是⊙O半径
∴⊙O与AC相切
教师活动:巡批,个别辅导,及时点评。
学生活动:完成练习。
设计意图:进一步巩固切线性质与判定的应用 。时间约15分钟。
环节五、目标检测,落实重点
1、如图9,⊙O是△ABC的内切圆,若∠OBC=15°,
∠OCB=40°,则∠A= 70 °
2、如图10,是⊙O的直径,是⊙O的切线,
为切点,连结交⊙O于点,连结,
若,则下列结论正确的是(A )
A. B.
C. D.
3、如图11,在⊙O中,AB为⊙O的直径,AC是弦,
,.
(1)求∠AOC的度数;
(2)P为直径BA延长线上的一点,
当CP与⊙O相切时,求PO的长;
解:(1)∵OC=OA ,∠OAC=60°∴∠CAO=∠OAC=60°
∴∠AOC=60°
(2)∵CP与⊙O相切 ∴OC⊥PC ∴∠PCO=90°
∵∠AOC=60° ∴OP=2CO=2×4=8
4、如图12, AB是⊙O的弦,点C是的中点, 直线CD∥AB.
求证:CD是⊙O的切线.
证明:连结OC. ∵C是的中点, ∴OC⊥AB.
∵CD∥AB, ∴OC⊥CD, ∴CD是⊙O的切线.
设计意图:根据具体情况进行。
环节六、拓展探索,展翅高飞
如图14,如图,在△ABC中,AB=AC,内切圆O与边BC、AC、AB分别切于D、E、F.(1)求证:BF=CE;
(2)连接AD,△ACD是什么三角形?
(3)若∠C=30°,,求AC.
设计意图:供学有余力的学生完成。
【板书】
图1
图2
图3
图4
图5
图6
A
B
O
·
C
图7
图8
图8
图9
图10
图11
图12
图14
【教学目标】
(1)知识与技能
①通过再现切线的判定和性质的形成过程及以题点知的练习回顾知识,并形成相应的知识结构;
②举例说明切线的性质与判定的应用,简要说出“切线”与“垂直”的密切关系(“半径”纽带的辅助作用);
③通过题组训练,有效提升应用切线的判定和性质解决问题的技能。
(2)过程与方法
①借助典型例题交流学习,发现通性,归纳分享解题思路和一般规律;
②类比例题与技能训练题的解题通性方法,分析对几何图形的分解与知识之间的转化技巧。
(3)情感、态度与价值观
说出切线在解决直线与圆的相关问题的作用,克服复习疲态,体会“课课有新知”,逐渐树立获取解题思路和方法的类比与归纳意识。
【教学重点】切线的性质和判定的应用。
【教学难点】判定切线的证明方法。
【设计说明】本课时是九年级总复习《圆》中的第4节,前面学生已复习了圆的基本概念、圆中的计算以及与圆的位置关系。本设计面向中下层次学生。针对切线的判定与性质在证明题、计算题中有较多的应用,所以本设计定位是切线判定的证明方法归纳总结,利用切线性质进行线段和角等简单计算的训练。
【教学流程】
【教学过程】
环节一、经典再现,认识切线
教师活动:在黑板上画出认识切线的关系图:从“直线与圆的位置关系”到“切线的定义”到“直线与圆相切时,d=r”到“切线的判定与性质”。
学生活动:观察关系图,再次经历切线的认识过程。
设计意图:让学生再次经历知识的形成过程,并由此引出课题——切线判定与性质,时间约2分钟。
环节二、以题点知,回顾应用
如图1,等腰△OAB中,OA=OB,AB=10
(1)⊙O与AB相切于C点,则AC= 5 ;
(2)若C点是AB的中点,⊙O经过C点,则⊙O和AB的位置关系是 相切
教师活动:以练习点出知识点(切线性质、判定)
学生活动:完成练习。
设计意图:以练习唤起学生对知识点的回忆,达到回顾知识点的目的,同时为例题作铺垫。时间约3分钟。
环节三、典例分析,学习共享
例、如图2,在△ABC中,CA=CB,AB的中点为点D,
当⊙D恰与CA相切于E点,求证:BC也是⊙D的切线。
证明:(2)连接DE,过D点作DF⊥CB于F点
∵⊙D恰与CA相切于E点, ∴DE⊥CA ∵DF⊥CB
∴∠AED=∠BFD=90° ∵CA=CB,∴∠A=∠B
∵AB的中点为点D ∴AD=BD ∴△ADE≌△BDF ∴DE=DF
∵DE是⊙D半径 ∴DF是⊙D半径 ∴BC也是⊙D的切线
(另外,可以也连接CD,用角平分线性质定理证明DE=DF)
教师活动:引导学生归纳常见判定切线的基本证明方法,
学生活动:先限时5分钟独立完成例题,然后小组合作归纳判定切线的证明方法。
设计意图:巩固切线的基本判定方法是本课的重点,这里先给足够时间学生独立完成例题,然后师生共享解题思路,达到学生自主学习的目的。时间约15分钟。
环节四、技能训练,提高有效
1、如图3,A、B在⊙O上,AC是⊙O的切线,
∠B=70°,则∠OAB= 70 °,∠BAC= 20 °
2、如图4,PA、PB分别与⊙O切于A、B点,
若PA=10,∠APO=25°,则PB= 10 ,∠APB= 50 °
3、如图5,AB是⊙O的直径,AB=AC,
(1)若AC是⊙O的切线,则∠C=_45_°.
(2)若∠B=45°,则AC与⊙O的位置关系是 相切
4、如图6,AB与⊙O相切于A点,AB=4,BO=5
则⊙O的半径为 3 。
5、如图7,两个同心圆的半径分别为3cm和5cm,弦AB与
小圆相切于点C,则AB的长为(D)
A.4cm B.5cm C.6cm D.8cm
6、如图8,已知O为∠BAC平分线上一点,
OD⊥AB于D, 以O为圆心,OD为半径作⊙O.
求证:⊙O与AC相切.
证明:过O点作OE⊥AC于E
∵OA平分∠BAC,OD⊥AB
∴OD=OE
∵OD为⊙O半径
∴OE是⊙O半径
∴⊙O与AC相切
教师活动:巡批,个别辅导,及时点评。
学生活动:完成练习。
设计意图:进一步巩固切线性质与判定的应用 。时间约15分钟。
环节五、目标检测,落实重点
1、如图9,⊙O是△ABC的内切圆,若∠OBC=15°,
∠OCB=40°,则∠A= 70 °
2、如图10,是⊙O的直径,是⊙O的切线,
为切点,连结交⊙O于点,连结,
若,则下列结论正确的是(A )
A. B.
C. D.
3、如图11,在⊙O中,AB为⊙O的直径,AC是弦,
,.
(1)求∠AOC的度数;
(2)P为直径BA延长线上的一点,
当CP与⊙O相切时,求PO的长;
解:(1)∵OC=OA ,∠OAC=60°∴∠CAO=∠OAC=60°
∴∠AOC=60°
(2)∵CP与⊙O相切 ∴OC⊥PC ∴∠PCO=90°
∵∠AOC=60° ∴OP=2CO=2×4=8
4、如图12, AB是⊙O的弦,点C是的中点, 直线CD∥AB.
求证:CD是⊙O的切线.
证明:连结OC. ∵C是的中点, ∴OC⊥AB.
∵CD∥AB, ∴OC⊥CD, ∴CD是⊙O的切线.
设计意图:根据具体情况进行。
环节六、拓展探索,展翅高飞
如图14,如图,在△ABC中,AB=AC,内切圆O与边BC、AC、AB分别切于D、E、F.(1)求证:BF=CE;
(2)连接AD,△ACD是什么三角形?
(3)若∠C=30°,,求AC.
设计意图:供学有余力的学生完成。
【板书】
图1
图2
图3
图4
图5
图6
A
B
O
·
C
图7
图8
图8
图9
图10
图11
图12
图14
同课章节目录
