2020-2021学年初中数学人教版七年级下册7.2.1 用坐标表示地理位置导学课件(27张)
文档属性
| 名称 | 2020-2021学年初中数学人教版七年级下册7.2.1 用坐标表示地理位置导学课件(27张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 605.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 11:48:42 | ||
图片预览





文档简介
第七章 平面直角坐标系
第19课时 用坐标表示地理位置
目录
01
名师导学
02
课堂讲练
03
分层训练
名师导学
A. 确定平面内某一点的位置一般需要_______个数据.
1. 第24届冬季奥林匹克运动会将于2022年在北京市和张家口市联合举行. 以下能够准确表示张家口市地理位置的是( )
A. 离北京市200 km B. 在河北省
C. 在宁德市北方 D. 东经114.8°,北纬40.8°
2
D
课堂讲练
典型例题
知识点1:用坐标表示地理位置
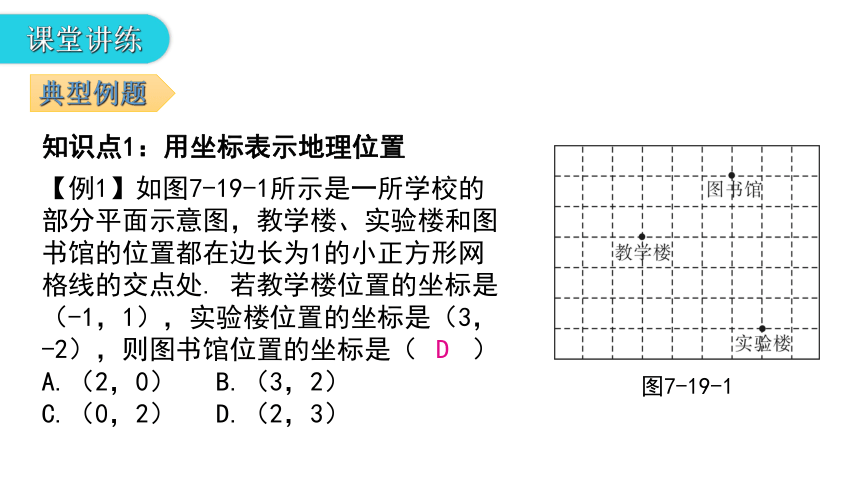
【例1】如图7-19-1所示是一所学校的部分平面示意图,教学楼、实验楼和图书馆的位置都在边长为1的小正方形网格线的交点处. 若教学楼位置的坐标是(-1,1),实验楼位置的坐标是(3,-2),则图书馆位置的坐标是( )
A.(2,0) B.(3,2)
C.(0,2) D.(2,3)
D
图7-19-1
思路点拨:根据已知点坐标得出原点位置,进而得出其他位置的坐标.
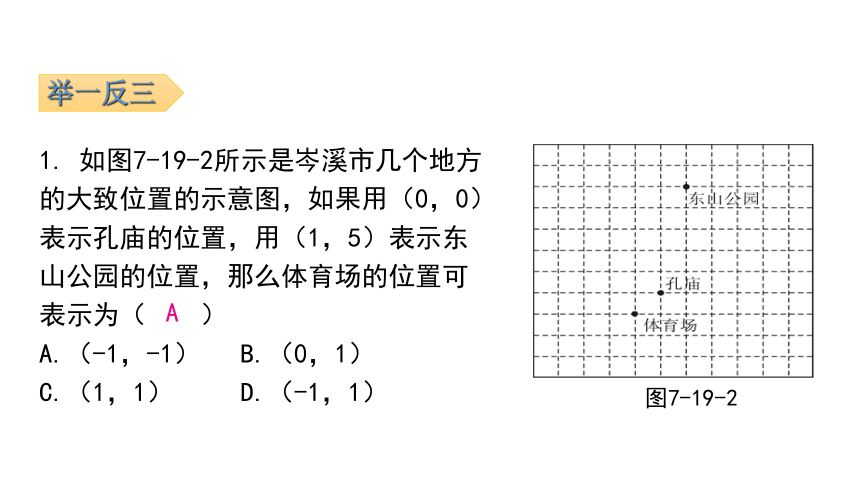
1. 如图7-19-2所示是岑溪市几个地方的大致位置的示意图,如果用(0,0)表示孔庙的位置,用(1,5)表示东山公园的位置,那么体育场的位置可表示为( )
A.(-1,-1) B.(0,1)
C.(1,1) D.(-1,1)
A
举一反三
图7-19-2
典型例题
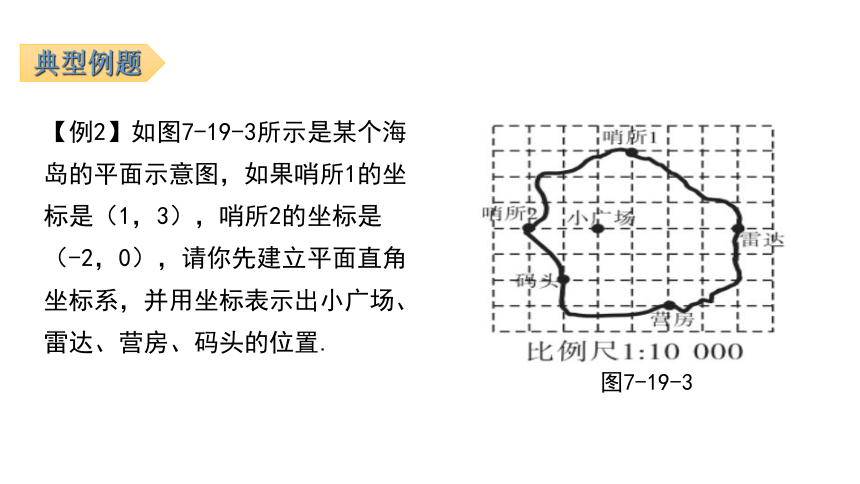
【例2】如图7-19-3所示是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
图7-19-3
思路点拨:利用已知点的坐标确定原点位置,作出平面直角坐标系再求解.
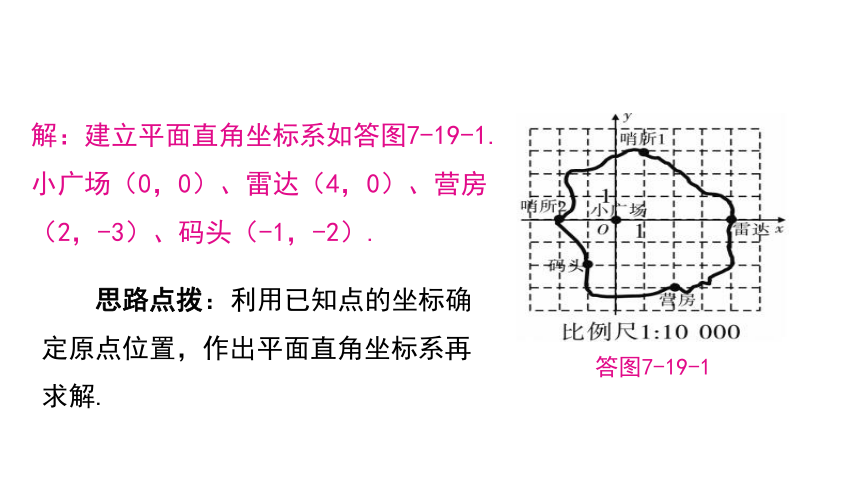
答图7-19-1
解:建立平面直角坐标系如答图7-19-1.
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2).
举一反三
2. 如图7-19-4,一个小正方形网格的边长表示50 m,A同学上学时从家中出发,先向东走250 m,再向北走50 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)B同学家的坐标是______________ ;
(3)若C同学家的坐标为(-150,100),请你在你所建的直角坐标系中,描出表示C同学家的点.
(200,150)
图7-19-4
解:(1)建立平面直角坐标系如答图7-19-2.
(3)表示C同学家的点如答图7-19-2.
答图7-19-1
【例3】点A的位置如图7-19-5,则关于点A的位置,下列说法正确的是( )
A. 距点O 4 km处
B. 北偏东40°方向上4 km处
C. 在点O北偏东50°方向上4 km处
D. 在点O北偏东40°方向上4 km处
思路点拨:根据点的位置确定方向以及距离.
D
知识点2:用方向和距离表示地理位置
典型例题
图7-19-5
3. 如图7-19-6,点O,M,A,B,C在同一平面内,若规定点A的位置记为(50,20°),点B的位置记为(30,60°). 则图中点C的位置应记为( )
A.(60°,30) B.(110°,34)
C.(34,4°) D.(34,110°)
举一反三
D
图7-19-6
分层训练
【A 组】
1. 以下描述中,能确定具体位置的是( )
A. 万达电影院2排 B. 距薛城高铁站2 km
C. 北偏东30° D. 东经106°,北纬31°
D
2. 生态园位于县城东北方向5 km处,下列选项表示准确的是( )
B
3. 小明住在学校正东200 m处,从小明家出发,向北走150 m就到了李华家,若选取李华家为原点,分别以正东、正北方向为x,y轴正方向建立平面直角坐标系,则学校的坐标为( )
A. (-150,-200) B. (-200,-150)
C. (0,-200) D. (150,200)
B
4. 如图7-19-7,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置是______________
_____________.
南偏西15°方向
50海里处
图7-19-7
5. 如图7-19-8,某校七年级的同学从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8 km到A处,又往正南方向走4 km到B处,又折向正东方向走6 km到C处,再折向正北方向走8 km到D处,最后又往正东方向走2 km才到探险处P,以点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2 km为一个长度单位建立直角坐标系.
(1)在直角坐标系中画出探险路线图;
(2)分别写出点A,B,C,D,P的坐标.
解:(1)如答图7-19-3.
(2)点A,B,C,D,P的坐标分别是(-8,0),(-8,-4),(-2,-4),(-2,4),(0,4).
图7-19-8
答图7-19-3
6. 如图7-19-9,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的平面直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
图7-19-9
答图7-19-4
解:(1)建立平面直角坐标系如答图7-19-4,图书馆(B)位置的坐标为(-3,-2).
(2)标出体育馆位置C如答图7-19-4,观察可得,三角形ABC中BC边长为5,BC边上的高为4,
∴SABC= ×5×4=10.
7. 如图7-19-10,是某战役缴获敌人防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3). 另有情报得知敌军指挥部的坐标为(-3,-2). 请问你能找到敌军的指挥部吗?
【B 组】
图7-19-10
答图7-19-5
解:如答图7-19-5,敌军指挥部在点C处.
8. 天气晴朗时,一个人能看到大海的最远距离s(km)可用公式s2=16.9h来估计,其中h (m)是眼睛离海平面的高度.
(1)如果一个人站在岸边观察,当眼睛离海平面的高度是2.5 m时,能看到多远?
(2)如图7-19-11,货轮B与观望台A相距35海里,用方向和距离描述观望台A相对于货轮B的位置为_____________________.
南偏西60°方向35海里处
解:(1)当h=2.5时,s2=16.9×2.5=42.25,
∴s=-6.5(不符题意,舍去)或s=6.5.
答:当眼睛离海平面的高度是2.5 m时,能看到6.5 km远.
图7-19-11
9. 如图7-19-12所示是某一区域部落的分布点,现在为了更好地表示各部落分布点的位置,以O为原点建立平面直角坐标系.
(1)写出图甲中各部落点A,B,C,D,E,F位置分布的坐标;
(2)图乙是一台雷达探测该区域部落点得到的结果,若记图中部落A的位置为(2,90°),则其余各部落的位置分别是多少?
图7-19-12
甲
乙
解:(1)各部落的坐标分别为A(-2,-2),B(-5,4),
C(5,-4),D(0,-3),E(2,5),F(-3,0).
(2)其余各部落的位置分别为B(4,30°),C(4,240°),D(3,300°),E(6,120°).
10. 如图7-19-13,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
【C 组】
图7-19-13
(1)“东”“窗”和“柳”的坐标依次是________,_________和_________;
(2)将第1行与第3行对调,再将第4列与第6列对调,“里”由开始的坐标_________依次变换到_________和_________;
(3)“门”开始的坐标是(1,1),使它的坐标变换到(3,2),应该将哪两行对调,同时将哪两列对调?
(3,1)
(7,4)
(1,2)
(6,1)
(6,3)
(4,3)
解:(3)“门”开始的坐标是(1,1),使它的坐标变换到
(3,2),应该将第1行与第2行对调,同时将第1列与第3列对调.
第19课时 用坐标表示地理位置
目录
01
名师导学
02
课堂讲练
03
分层训练
名师导学
A. 确定平面内某一点的位置一般需要_______个数据.
1. 第24届冬季奥林匹克运动会将于2022年在北京市和张家口市联合举行. 以下能够准确表示张家口市地理位置的是( )
A. 离北京市200 km B. 在河北省
C. 在宁德市北方 D. 东经114.8°,北纬40.8°
2
D
课堂讲练
典型例题
知识点1:用坐标表示地理位置
【例1】如图7-19-1所示是一所学校的部分平面示意图,教学楼、实验楼和图书馆的位置都在边长为1的小正方形网格线的交点处. 若教学楼位置的坐标是(-1,1),实验楼位置的坐标是(3,-2),则图书馆位置的坐标是( )
A.(2,0) B.(3,2)
C.(0,2) D.(2,3)
D
图7-19-1
思路点拨:根据已知点坐标得出原点位置,进而得出其他位置的坐标.
1. 如图7-19-2所示是岑溪市几个地方的大致位置的示意图,如果用(0,0)表示孔庙的位置,用(1,5)表示东山公园的位置,那么体育场的位置可表示为( )
A.(-1,-1) B.(0,1)
C.(1,1) D.(-1,1)
A
举一反三
图7-19-2
典型例题
【例2】如图7-19-3所示是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置.
图7-19-3
思路点拨:利用已知点的坐标确定原点位置,作出平面直角坐标系再求解.
答图7-19-1
解:建立平面直角坐标系如答图7-19-1.
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2).
举一反三
2. 如图7-19-4,一个小正方形网格的边长表示50 m,A同学上学时从家中出发,先向东走250 m,再向北走50 m就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系;
(2)B同学家的坐标是______________ ;
(3)若C同学家的坐标为(-150,100),请你在你所建的直角坐标系中,描出表示C同学家的点.
(200,150)
图7-19-4
解:(1)建立平面直角坐标系如答图7-19-2.
(3)表示C同学家的点如答图7-19-2.
答图7-19-1
【例3】点A的位置如图7-19-5,则关于点A的位置,下列说法正确的是( )
A. 距点O 4 km处
B. 北偏东40°方向上4 km处
C. 在点O北偏东50°方向上4 km处
D. 在点O北偏东40°方向上4 km处
思路点拨:根据点的位置确定方向以及距离.
D
知识点2:用方向和距离表示地理位置
典型例题
图7-19-5
3. 如图7-19-6,点O,M,A,B,C在同一平面内,若规定点A的位置记为(50,20°),点B的位置记为(30,60°). 则图中点C的位置应记为( )
A.(60°,30) B.(110°,34)
C.(34,4°) D.(34,110°)
举一反三
D
图7-19-6
分层训练
【A 组】
1. 以下描述中,能确定具体位置的是( )
A. 万达电影院2排 B. 距薛城高铁站2 km
C. 北偏东30° D. 东经106°,北纬31°
D
2. 生态园位于县城东北方向5 km处,下列选项表示准确的是( )
B
3. 小明住在学校正东200 m处,从小明家出发,向北走150 m就到了李华家,若选取李华家为原点,分别以正东、正北方向为x,y轴正方向建立平面直角坐标系,则学校的坐标为( )
A. (-150,-200) B. (-200,-150)
C. (0,-200) D. (150,200)
B
4. 如图7-19-7,一艘船在A处遇险后向相距50海里位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置是______________
_____________.
南偏西15°方向
50海里处
图7-19-7
5. 如图7-19-8,某校七年级的同学从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8 km到A处,又往正南方向走4 km到B处,又折向正东方向走6 km到C处,再折向正北方向走8 km到D处,最后又往正东方向走2 km才到探险处P,以点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2 km为一个长度单位建立直角坐标系.
(1)在直角坐标系中画出探险路线图;
(2)分别写出点A,B,C,D,P的坐标.
解:(1)如答图7-19-3.
(2)点A,B,C,D,P的坐标分别是(-8,0),(-8,-4),(-2,-4),(-2,4),(0,4).
图7-19-8
答图7-19-3
6. 如图7-19-9,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的平面直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到三角形ABC,求三角形ABC的面积.
图7-19-9
答图7-19-4
解:(1)建立平面直角坐标系如答图7-19-4,图书馆(B)位置的坐标为(-3,-2).
(2)标出体育馆位置C如答图7-19-4,观察可得,三角形ABC中BC边长为5,BC边上的高为4,
∴SABC= ×5×4=10.
7. 如图7-19-10,是某战役缴获敌人防御工事坐标地图的碎片,依稀可见:一号暗堡A的坐标为(4,3),五号暗堡B的坐标为(-2,3). 另有情报得知敌军指挥部的坐标为(-3,-2). 请问你能找到敌军的指挥部吗?
【B 组】
图7-19-10
答图7-19-5
解:如答图7-19-5,敌军指挥部在点C处.
8. 天气晴朗时,一个人能看到大海的最远距离s(km)可用公式s2=16.9h来估计,其中h (m)是眼睛离海平面的高度.
(1)如果一个人站在岸边观察,当眼睛离海平面的高度是2.5 m时,能看到多远?
(2)如图7-19-11,货轮B与观望台A相距35海里,用方向和距离描述观望台A相对于货轮B的位置为_____________________.
南偏西60°方向35海里处
解:(1)当h=2.5时,s2=16.9×2.5=42.25,
∴s=-6.5(不符题意,舍去)或s=6.5.
答:当眼睛离海平面的高度是2.5 m时,能看到6.5 km远.
图7-19-11
9. 如图7-19-12所示是某一区域部落的分布点,现在为了更好地表示各部落分布点的位置,以O为原点建立平面直角坐标系.
(1)写出图甲中各部落点A,B,C,D,E,F位置分布的坐标;
(2)图乙是一台雷达探测该区域部落点得到的结果,若记图中部落A的位置为(2,90°),则其余各部落的位置分别是多少?
图7-19-12
甲
乙
解:(1)各部落的坐标分别为A(-2,-2),B(-5,4),
C(5,-4),D(0,-3),E(2,5),F(-3,0).
(2)其余各部落的位置分别为B(4,30°),C(4,240°),D(3,300°),E(6,120°).
10. 如图7-19-13,我们把杜甫的《绝句》整齐排列放在平面直角坐标系中.
【C 组】
图7-19-13
(1)“东”“窗”和“柳”的坐标依次是________,_________和_________;
(2)将第1行与第3行对调,再将第4列与第6列对调,“里”由开始的坐标_________依次变换到_________和_________;
(3)“门”开始的坐标是(1,1),使它的坐标变换到(3,2),应该将哪两行对调,同时将哪两列对调?
(3,1)
(7,4)
(1,2)
(6,1)
(6,3)
(4,3)
解:(3)“门”开始的坐标是(1,1),使它的坐标变换到
(3,2),应该将第1行与第2行对调,同时将第1列与第3列对调.
