人教版数学七年级下册课件:5.1.3同位角 内错角 同旁内角(17张)
文档属性
| 名称 | 人教版数学七年级下册课件:5.1.3同位角 内错角 同旁内角(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览



文档简介
5.1 相交线
第 3 课时
第五章 相交线与平行线
风筝起源于中国,是一门古老的艺术.相传最早在春秋战国时期,墨翟“费时三年,斫木为鸢,飞升天空 ”.汉朝时期,蔡伦发明造纸术,开始以纸为材料制作;唐朝时期,有人加入了琴弦,风一吹,就发出像古筝那样的声音,始叫“风筝” !随着马可·波罗自中国返回欧洲后,风筝传到世界各地,据说莱特兄弟发明飞机就是源于对风筝的着迷.
一、创设情景,引入主题
一、创设情景,引入主题
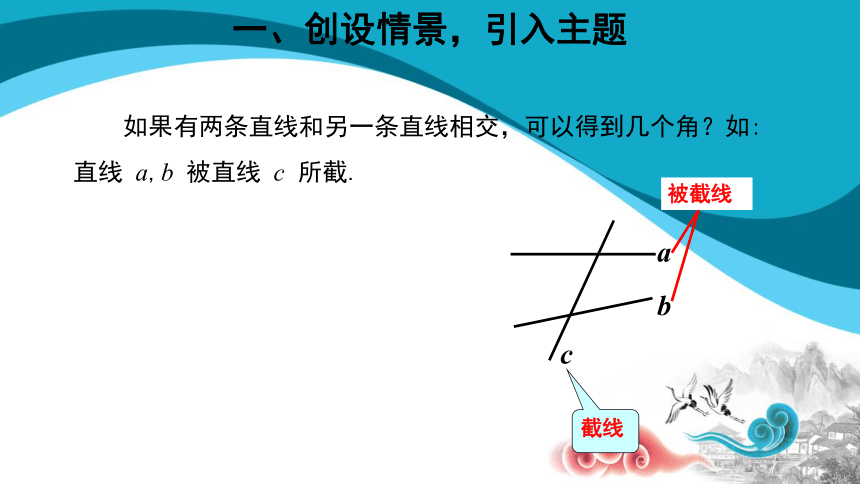
如果有两条直线和另一条直线相交,可以得到几个角?如:直线 a,b 被直线 c 所截.
a
b
c
截线
被截线
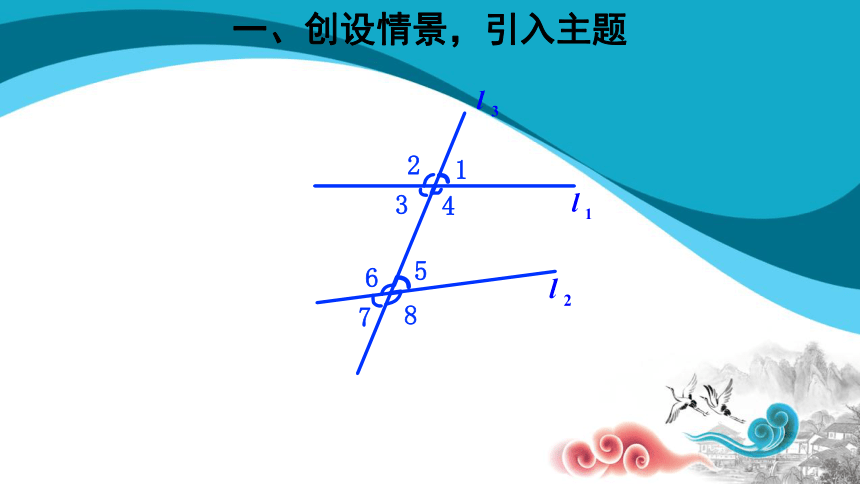
一、创设情景,引入主题
一、创设情景,引入主题
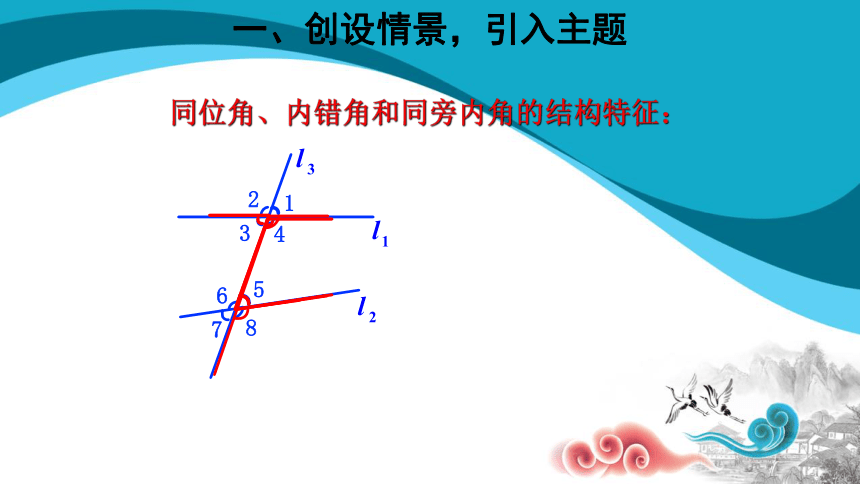
同位角、内错角和同旁内角的结构特征:
一、创设情景,引入主题
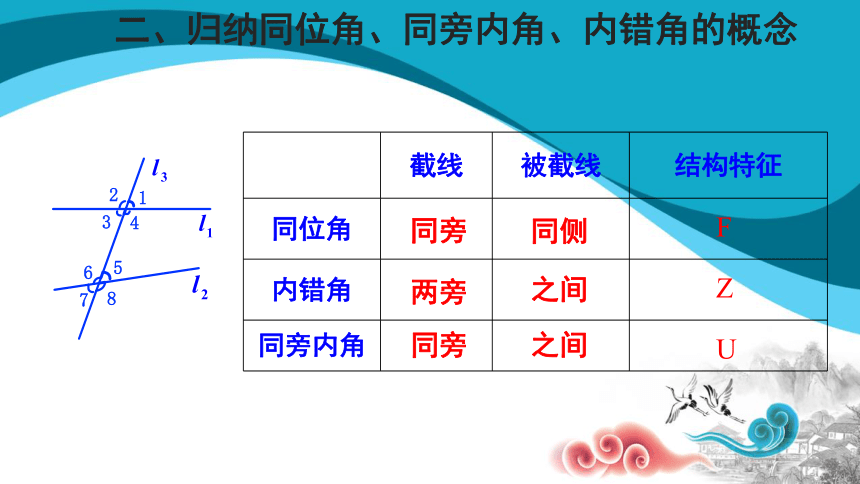
截线
被截线
结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
二、归纳同位角、同旁内角、内错角的概念
上述三类角类似于对应角都是成对出现.不能说哪个角是同位角、内错角等.
注意:
二、归纳同位角、同旁内角、内错角的概念
注:此图片是动画缩略图,如需使用此资源,请插入动画“同位角、内错角、同旁内角”.
二、归纳同位角、同旁内角、内错角的概念
三、巩固概念,深化理解
问题:(1)图中可以看成是哪两条直线被哪条直线所截?
(2)哪些角成同位角、内错角、同旁内角?
三、巩固概念,深化理解
问题:(1)∠1与∠2是不是同位角、内错角、同旁内角?
(2)如果是,找出是哪两条直线被哪条直线所截形成的.
追问:旋转到什么位置能构成同位角、内错角、同旁内角呢?
(1)若ED,BF 被AB所截,则∠1与_____是同位角.
∠2
(2)若ED,BC 被AF所截,则∠3与_____是内错角.
∠4
(3)∠1与∠3是 AB和AF 被_____所截构成的_____角.
DE
内错
(4)∠2与∠4是_____和_____被BC所截构成的______角.
AB
AF
同位
四、应用概念,发展图形
例1
例2 如图:直线 DE,BC 被直线 AB 所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠3相等吗?∠1与∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
四、应用概念,发展图形
练习 ∠A 与∠8是哪两条直线被第三条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠4呢?
∠A与∠4是 AC 与 DE 被 AB 所截,是同位角.
∠A 与∠8是 AB 与 DE 被 AC 所截,是内错角.
∠A与∠5是 AB 与 DE 被 AC 所截,是同旁内角.
四、应用概念,发展图形
E
D
C
B
A
8
7
6
5
4
3
2
1
五、归纳小结
教材习题5.1 第11题
六、布置作业
再 见
第 3 课时
第五章 相交线与平行线
风筝起源于中国,是一门古老的艺术.相传最早在春秋战国时期,墨翟“费时三年,斫木为鸢,飞升天空 ”.汉朝时期,蔡伦发明造纸术,开始以纸为材料制作;唐朝时期,有人加入了琴弦,风一吹,就发出像古筝那样的声音,始叫“风筝” !随着马可·波罗自中国返回欧洲后,风筝传到世界各地,据说莱特兄弟发明飞机就是源于对风筝的着迷.
一、创设情景,引入主题
一、创设情景,引入主题
如果有两条直线和另一条直线相交,可以得到几个角?如:直线 a,b 被直线 c 所截.
a
b
c
截线
被截线
一、创设情景,引入主题
一、创设情景,引入主题
同位角、内错角和同旁内角的结构特征:
一、创设情景,引入主题
截线
被截线
结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
二、归纳同位角、同旁内角、内错角的概念
上述三类角类似于对应角都是成对出现.不能说哪个角是同位角、内错角等.
注意:
二、归纳同位角、同旁内角、内错角的概念
注:此图片是动画缩略图,如需使用此资源,请插入动画“同位角、内错角、同旁内角”.
二、归纳同位角、同旁内角、内错角的概念
三、巩固概念,深化理解
问题:(1)图中可以看成是哪两条直线被哪条直线所截?
(2)哪些角成同位角、内错角、同旁内角?
三、巩固概念,深化理解
问题:(1)∠1与∠2是不是同位角、内错角、同旁内角?
(2)如果是,找出是哪两条直线被哪条直线所截形成的.
追问:旋转到什么位置能构成同位角、内错角、同旁内角呢?
(1)若ED,BF 被AB所截,则∠1与_____是同位角.
∠2
(2)若ED,BC 被AF所截,则∠3与_____是内错角.
∠4
(3)∠1与∠3是 AB和AF 被_____所截构成的_____角.
DE
内错
(4)∠2与∠4是_____和_____被BC所截构成的______角.
AB
AF
同位
四、应用概念,发展图形
例1
例2 如图:直线 DE,BC 被直线 AB 所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠3相等吗?∠1与∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
四、应用概念,发展图形
练习 ∠A 与∠8是哪两条直线被第三条直线所截的角?它们是什么关系的角?∠A与∠5呢?∠A与∠4呢?
∠A与∠4是 AC 与 DE 被 AB 所截,是同位角.
∠A 与∠8是 AB 与 DE 被 AC 所截,是内错角.
∠A与∠5是 AB 与 DE 被 AC 所截,是同旁内角.
四、应用概念,发展图形
E
D
C
B
A
8
7
6
5
4
3
2
1
五、归纳小结
教材习题5.1 第11题
六、布置作业
再 见
